熔盐堆(Molten Salt Reactor, MSR)的概念源自于美国20世纪50~70年代橡树岭国家实验室(Oak Ridge National Laboratory, ORNL)建造或设计的空间实验堆(Aircraft Reactor Experiment, ARE)^[1-2]、熔盐实验堆(Molten Salt Reactor Experiment, MSRE)^[3-4]、熔盐增殖堆(Molten Salt Breeding Reactor, MSBR)^[5-6]、低浓化熔盐堆(Denatured Molten Salt Reactor, DMSR)^[7]等实验堆。2001~2003年，ORNL、桑地亚国家实验室(Sandia National Laboratories, SNL)和加州大学伯克利分校(University of California Berkeley, UCB)共同发展了先进高温堆(Advanced High-Temperature Reactor, AHTR)的概念，后正式命名为氟盐冷态高温堆(Fluoride Salt Cooled High Temperature Reactor, FHR)^[8-10]。2011年，中国科学院启动了“未来先进核裂变能——钍基熔盐堆核能系统”战略先导专项TMSR，其首期计划建成2 MW液态燃料熔盐堆实验堆和10 MW固态燃料熔盐实验堆^[11]。

反应堆的衰变热主要来自于裂变产物、锕系核素、活化产物，其中裂变产物是衰变热的主要来源，正常运行时约占总衰变热的97%。对于任何一种固定燃料类型反应堆来讲，通常关心的是停堆后反应堆内衰变热的变化特性，这对反应堆余热排出系统的设计、冷却剂丧失情况下的事故安全分析、乏燃料的安全运输及储存都具有重要的参考价值。反应堆停堆后，堆内仍然存在大量衰变热，尤其是刚停堆的短时间内，堆内具有很大的释热能力，此时，如果反应堆内燃料元件无法得到很好的冷却，堆芯内的温度快速升高，甚至超过堆芯材料设计使用的温度上限，将导致堆芯烧毁，反应堆内重大安全事故很多都是与堆内传热和冷却问题有关，为了保证反应堆安全运行，必须保证在任何工况下都能够及时排除堆芯余热。相对固定燃料类型反应堆而言，对使用²³⁵U作为裂变材料的熔盐堆来讲，停堆衰变热的产生与停堆后的衰变规律与其他以²³⁵U作为裂变材料的固定燃料类型反应堆基本相同，同样应该保证停堆后的余热带载出问题，除此之外，熔盐堆相对固定燃料类型反应堆而言，熔盐堆在正常运行工况下衰变热会充满整个主回路系统及关键设备之内，并持续产生热量，因此依然需要考虑其衰变热功率对管道的热工水力安全设计带来的影响。

熔盐堆正常运行工况下，载有衰变热的裂变产物核素会随燃料盐的流动被分散在整个主回路管道以及相关热工水力连接区域，包括热管段、冷管段、主泵、主换热器等区域。正常运行达到平衡时，总衰变热约占反应堆总热功率的7%，这是一个很可观的数值，这些衰变热在主回路管道及设备内将被视为持续发热的热源，在正常运行工况下设备内衰变热若不能准确估算并从设计上确保热量的带出，很有可能会使得主管道材料及设备在超设计温度下服役，最终可能降低材料及设备使用寿命，甚至酿成破口及设备损坏等严重事故，最终导致放射性源项的释放。在功率控制方面，TMSR-LF1通过固定出入口温度以及固定流量实现功率的稳定输出，在不考虑管道及设备热损失的情况下，理论上堆芯活性区出入口温度与换热器进出口温度是一致的，但倘若主回路管道及设备内存在稳定热源，那么换热器处进出口温度将不再与堆芯进出口温度保持一致，是主回路系统及设备的保温层设计以及反应堆进出口温度的监测及控制均需进行考虑的关键问题，这也是流动燃料类型反应堆与固定燃料类型反应堆的一大区别。

2 MW TMSR-LF1在工程设计中所使用到的堆芯衰变热分析程序为ORIGEN-S程序，该程序在核素燃耗分析、源项分析以及衰变热等分析方面被广泛应用，该程序为典型的静态点燃耗程序，这类程序除ORIGENS以外常用的还有ORIGEN、ORIGEN2、KORIGEN、DECOM、FISPIN等。这些程序尽管可以通过外部调用实现分区燃耗，但每个区域的燃耗方程本质上均为固定的点燃耗，无法对裂变产物在不同区域间的流动问题进行分析。另外，通过这类点燃耗程序的外部调用不足以实现对流动问题的分析，这主要考虑到每个燃耗时间步长一般较长，而燃耗演化链中不同核素的半衰期相差甚大，微分方程是典型的刚性方程，对于短寿命的核素，要求对求解步长有精细的要求，而且反复外部读取文件及数据也大大降低了解决问题的效率，在时间及精度方面均不能满足需求，显然是不可取的。本文基于Mathematica 7.0程序建立了熔盐堆主回路系统的衰变热的动力学特性分析程序，并与参考程序ORIGENS进行了初步验证，对不考虑流动效应情况下的静态燃耗结果进行了对比，二者在全燃耗寿期内的计算偏差在±4%范围内，初步验证了数学模型正确性及所使用核数据的合理性。同时对中国科学院上海应用物理研究所的TMSR-LF1方案设计阶段的一种方案在燃料盐流动情况下主回路系统衰变热随时间的流动演化规律、动态分布特性进行了分析。

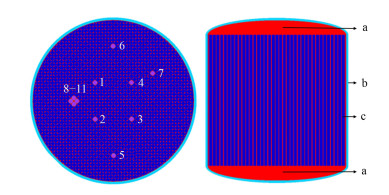
TMSR-LF1堆芯物理参数计算模型如图 1所示，堆芯直径为190 cm，高度为180 cm。堆芯主容器和堆内金属支撑结构件使用ASME-N10003镍基合金材料。控制棒、实验与测量装置、中子源等布置在相应的11个功能通道中。其中1#、2#、3#、4#、5#、6#为控制棒通道，7#为中子源通道，8#、9#、10#、11#为辐照实验与测量通道。在计算中子通量及中子能谱时使用了SCALE6.1程序包中的三维蒙特卡罗输运程序KENO-Ⅵ模块，在计算静态燃耗时使用的验证程序为SCALE6.1程序包中的TRITON^[12]控制模块，该模块主要调用ORIGEN-S^[13]功能模块进行核素燃耗计算。

图 1

图 1 堆芯模型 a.燃料盐，b.反应堆容器，c.堆芯石墨组件 Figure 1 Reactor core model a. Fuel salt, b. Reactor vessel, c. Core graphite

堆芯总体设计参数：热功率2 MW；寿命20 a；首批装料满功率运行天数300 d；反应堆进、出口温度为600 ℃、650 ℃；燃料盐LiF-BeF₂-UF₄；铀燃料富集度19.75%；二回路冷却剂FNaBe；主回路熔盐额定流量2.24×10⁴ cm³·s^-1；燃料组件材料为石墨；主容器及堆内构件的主要材料为ASME-N10003；泵碗鼓泡气体类型为氦气。

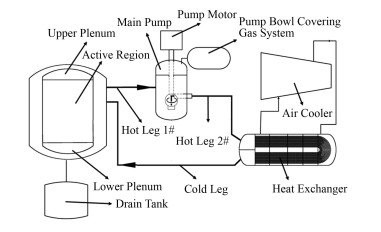
TMSR-LF1堆芯及主回路系统布局见图 2，燃料盐从堆芯上部出口流出至热管段，流经主泵，然后经过双熔盐换热器到主回路系统的冷管段，再从堆芯上部流入反应堆，经过下降环腔到达下腔室，自上而下流入堆芯活性区，二回路通过双熔盐换热器将主回路的热量交换至二回路熔盐，再通过熔盐空冷风机将二回路熔盐的热量带到空气环境中。

图 2

图 2 TMSR-LF1系统示意图 Figure 2 Schematic diagram of TMSR-LF1 system

待求解物理量为裂变产物核素的原子密度在主回路系统不同空间不同时刻的量，为实现对不同空间核素演化的模拟以及不同空间之间的流动过程模拟，首先对主回路系统进行了空间分区，并对每个空间添加流动项，这也是实现核素流动分布分析的两个关键考虑。

根据图 2所示的主回路系统结构及布局沿流动方向进行了一维空间的划分，建立数学模型时将主回路系统近似等效为8个空间区域，即堆芯活性区、上腔室、热管段、主泵、换热器、冷管段以及下腔室，其中主泵位于热管段的中间，因此分析时将热管段分成两部分：热管段1#及热管段2#。每个空间均考虑待求解核素由²³⁵U裂变的产生项、由其他母核通过核反应及衰变的产生贡献及待求解核素自身由于衰变及核反应的消失项，另外对相邻空间之间添加了流入项及流出项，从而建立了含空间项含流动项的联立微分方程组，如式(1)所示，理论模型的处理及假设如下：

1) 假设模型是一维流动问题，不考虑管道内流场的径向流动。

2) 假设熔盐流体体积不可压缩，假设密度不变。

3) 不考虑裂变产物在主回路系统中的化学反应、物理吸附及扩散等效应。

4) 保守起见，主回路衰变热的分析过程不考虑裂变产物气体的在线去除。

5) 保守起见，不考虑主回路系统到包容体及二回路的泄露与扩散。

式中：n=1, …, i, …，为待求解核素总个数；a=1, …, j, …，为主回路系统所划分的区域总个数；N_{i, j}[t]为待求解核素i在区域j中的原子密度；γ_{k, i}为核素k裂变产生核素i的裂变产额；σ_{k, f, j}为区域j中核素k的裂变反应微观截面；σ_{i, j}为区域j中核素i除裂变反应之外的核反应微观截面；Φ_j为区域j中平均中子通量密度；σ_{k→i, j}为区域j中核素k通过核反应产生核素i的微观截面；b_k→i为核素k通过衰变产生核素i的衰变分支比；λ_i^dec为核素i的衰变常数。

式(1)右侧第一项$ \sum\limits_{k=1}^{n}{{{\gamma }_{k, i}}}{{\sigma }_{k, f, j}}{{N}_{k, j}}[t]{{\mathit{\Phi} }_{j}} $代表区域j中核素i来自核素k的裂变产生率，具体表示形式如式(2)所示，裂变产额矩阵γ_{k, i}为n×n维矩阵，该矩阵为多数元素均为0的稀疏矩阵，对于非裂变核

素及具体问题中不包含的裂变核素矩阵元素均为0，本文主要考虑来自熔盐堆中裂变材料²³⁵U的裂变产额数据。

$ \sum\limits_{k=1}^{n}{{{\sigma }_{k\to i, j}}{{N}_{k, j}}[t]{{\mathit{\Phi} }_{j}}} $为区域j中核素i来自核素k与中子发生核反应的产生率，具体表示成式(3)的形式：

$ \sum\limits_{k=1}^{a}{{{b}_{k\to i}}\lambda _{k}^{\text{dec}}{{N}_{k, j}}[t]} $为区域j中核素i来自核素k的衰变产生率，写成矩阵形式则如式(4)所示，其中b_k→i是衰变分支比，为n×n维稀疏矩阵，λ_i^dec是衰变常数，为n×n维对角矩阵。

$ {{\sigma }_{k, f, j}}{{N}_{i, j}}[t]{{\mathit{\Phi} }_{j}} $为区域j中核素i的裂变消失率，其中$ {{\sigma }_{k, f, j}} $为一对角矩阵，如式(5)所示。

$ ({{\sigma }_{i, j}}-{{\sigma }_{i, f, j}}){{N}_{i, j}}[t]{{\mathit{\Phi} }_{j}} $为区域j中核素i除裂变反应之外的反应途径的消失率，表达形式与式(5)相近，在此不作展开。

$ \lambda _{i}^{\text{dec}}{{N}_{i, j}}[t] $为区域j中核素i的衰变消失率，衰变常数$ \lambda _{i}^{\text{dec}} $同式(4)中的$ \lambda _{i}^{\text{dec}} $对角矩阵。

$ \sum\limits_{m=1}^{a}{\lambda _{i,m\to j}^{\text{flowin}}{{N}_{i,m}}[t]=\sum\limits_{m=1}^{a}{\frac{V{{F}_{m\to j}}{{N}_{i.m}}[t]}{\text{Volum}{{\text{e}}_{j}}}}} $为核素i从区域m流入区域j的流入项，具体表示为式(6)的形式，$ V{{F}_{m\to j}} $为体积流量，该矩阵为a×a维区域流动转移矩阵，由于研究对象为一维单向流动问题，因此该矩阵元素中只在流动方向上相邻区域之间为非零，其余情况矩阵元素值为0，Volume_j为区域j中燃料盐体积；

$ \sum\limits_{m=1}^{a}{\lambda _{i, j\to m}^{\text{flowout}}{{N}_{i, j}}[t]=\sum\limits_{m=1}^{a}{\frac{V{{F}_{j\to m}}{{N}_{i.j}}[t]}{\text{Volum}{{\text{e}}_{j}}}}} $为核素i从区域j流出至区域m的流出项，表示形式同式(6)类似。

通过Mathematica对裂变产额、衰变常数、核素截面、体积及流量等输入参数进行读取，并对微分方程组进行数值求解，从而得到各区域核素浓度N_i.j[t]，进而得到各区域核素i的衰变热功率$ P_{i, j}^{\text{dec}}[t] $，如式(7)所示，其中$ Q_{i}^{\text{dec}} $为核素i单位活度衰变释放的能量：

求解时所有裂变产物初始化值均设为0。

Mathematica计算中所使用的核数据均为最新版本ENDFBVII.1的数据，包括裂变产额、半衰期及衰变分支比等数据。

为了验证程序在核素演化链处理上以及核数据选取上的正确性、合理性，在对衰变热的动态流动特性分析之前，首先对TMSR-LF1主回路系统流量为0的情况下全堆芯总衰变热进行了计算，并将计算结果与SCALE6.1中的TRITON燃耗控制模块计算结果进行了对比验证。对比结果见表 1，其中P_dec/FP为衰变热功率与满功率的比值。可以看出，计算结果与TRITON程序输出结果在全燃耗寿期(300 d)内的累积计算结果偏差均在±4%范围以内，符合较好。

表 1

表 1 反应堆启堆后总衰变热计算结果 Table 1 Calculation results of total decay heat after start-up of the reactor 停堆时间 Time after shutdown /d 参考值 (Pdec/FP) Reference value 计算值 (Pdec/FP) Calculated value 偏差 Relative deviation/% 1 6.40% 6.55% 2.37 2 6.50% 6.65% 2.34 3 6.55% 6.70% 2.28 10 6.69% 6.86% 2.52 30 6.77% 6.98% 3.20 100 6.84% 7.09% 3.69 200 6.87% 7.13% 3.81 300 6.88% 7.14% 3.88

表 1 反应堆启堆后总衰变热计算结果 Table 1 Calculation results of total decay heat after start-up of the reactor

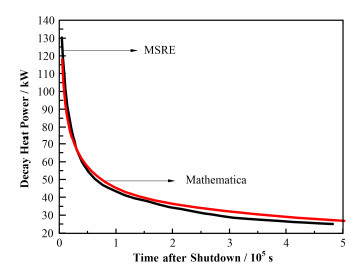
另外，选择了MSRE实验堆衰变热结果进行了对比^[14]。首先利用自编程序对MSRE实验堆衰变热数据进行了模拟，并与MSRE安全分析报告中的提供的衰变热曲线进行了对比，MSRE安全分析报告中提供的数据为10 MW热功率下连续运行1000 h停堆15 min后排盐罐中衰变热功率数据，对比结果如图 3所示，二者在停堆后15 min~140 h内，相对偏差在±2.76%范围内，符合较好。

图 3

图 3 Mathematica与MSRE实验堆衰变热数据比较 Figure 3 Comparison of decay heat data between Mathematica and MSRE

通过与现有燃耗分析程序以及MSRE实验堆提供的数据所作的对比，初步验证了所建立的数学模型及数值分析方法在燃耗链处理上是正确的，所使用的核数据及分析结果均是合理可靠的。

反应堆从临界状态到满功率运行工况时，整个启堆过程通常是缓慢的，操作流程也是复杂的。通常是通过缓慢提升控制棒，并结合堆内中子探测器的实时监测，使得堆芯功率缓慢提成并达满功率，对于实验堆其启堆过程会更加复杂、缓慢，同时在零功率实验阶段及低功率实验阶段其衰变热相对较少，根据额定设计功率进行模拟，其衰变热功率是最快能够达到平衡的。另外，真实的模拟MSR实验堆的启堆过程需结合详细的启堆运行及实验方案，模拟起来相对较难，因此为了便于模拟，仅对反应堆达满功率后的过程进行模拟，即假设反应堆热功率及燃料盐流量在0时刻均达额定功率及额定流量。

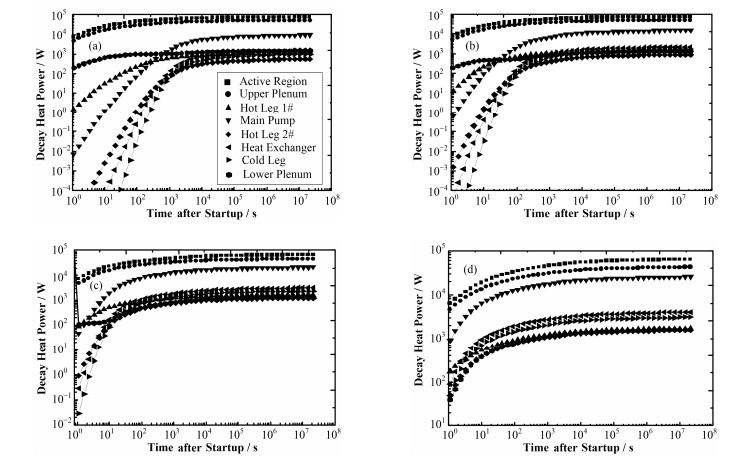
图 4为不同流量情况下，主回路系统衰变热的变化曲线。可以看出，不同流量情况下，各区域衰变热达到平衡所需时间有很大差异，且平衡浓度也会随流量而变化，堆芯活性区、上腔室、下腔室的变化趋势与堆外其他区域的变化趋势有所差异。流量增大时，堆芯活性区、上腔室、下腔室达到平衡的时间变长，而堆外其他区域流量越小其达到平衡所需时间越长，这主要取决于短寿命核素在堆外的衰变及流动所经历的时间。

图 4

图 4 衰变热随流量和时间的变化 (a) 2.24×102 cm3·s-1，(b) 2.24×103 cm3·s-1，(c) 2.24×104 cm3·s-1，(d) 2.24×105 cm3·s-1 Figure 4 Decay heat varies with flow rate and time (a) 2.24×102 cm3·s-1, (b) 2.24×103 cm3·s-1, (c) 2.24×104 cm3·s-1, (d) 2.24×105 cm3·s-1

表 2为不同流量情况下衰变热达平衡态时在主回路系统中的分布。正常工况下，即额定流量为2.24×10⁴ cm³∙s^-1，可见，各区域衰变热约在20 s就已趋平衡，达到平衡态时，堆芯活性区占46.7%，上腔室占31.8%，热管段1#占1.21%，主泵占14.6%，热管段1#占0.89%，换热器占2.21%，冷管段占1.67%，下腔室占0.94%。随着流量的增加，堆芯活性区及上腔室衰变热分别从53.64%、35.84%降低至44.06%、28.66%，主要由于裂变产物流出堆芯所导致；流量增加时，回路管道、主泵、换热器内的衰变热所占比例单调增加，而下腔室则出现先减小后增加的趋势，在流量为4.48×10³ cm³∙s^-1处有一拐点，这是由于从堆芯流入下腔室项逐渐增加以及下腔室裂变产生项减小两种效应的叠加所导致。

表 2

表 2 平衡态衰变热随流量的变化 Table 2 Decay heat varies with flow rate at equilibrium state 流量 Flow rate /cm3·s-1 不同区域衰变热占比Decay power ratio in different regions/% 堆芯活性区 Active region 上腔室 Upper plenum 热管段1# Hot leg 1# 主泵 Main pump 热管段2# Hot leg 2# 换热器 Heat exchanger 冷管段 Cold leg 下腔室 Lower plenum 2.24×102 53.64 35.84 0.79 6.62 0.40 0.95 0.71 1.05 2.24×103 50.40 34.03 1.06 10.31 0.62 1.52 1.14 0.92 4.48×103 49.29 33.39 1.13 11.59 0.70 1.72 1.29 0.90 1.12×104 47.81 32.49 1.19 13.30 0.81 1.99 1.50 0.91 2.24×104 46.71 31.78 1.21 14.59 0.89 2.21 1.67 0.94 4.48×104 45.74 31.05 1.22 15.78 0.97 2.42 1.84 0.99 1.12×105 44.83 30.14 1.20 17.04 1.05 2.65 2.03 1.06 2.24×105 44.43 29.57 1.19 17.69 1.09 2.78 2.14 1.11 2.24×106 44.06 28.66 1.16 18.54 1.15 2.96 2.29 1.18

表 2 平衡态衰变热随流量的变化 Table 2 Decay heat varies with flow rate at equilibrium state

表 3为熔盐堆停堆后总衰变热随冷却时间的变化，同时给出了裂变产物、锕系核素及活化产物所占衰变热比例。停堆后，燃料盐被排放至卸料罐，由卸料罐中的余热冷却系统将卸料盐衰变热进行载出，以保证排盐罐能够安全地储存乏燃料盐。美国橡树岭国家实验室设计的MSRE，其余热排出系统余热排出能力设计值为反应堆满功率的1%，也就相当于停堆后1 h后的衰变热功率，可作为TMSR-LF1余热排出系统的余热排出能力设计参考。

表 3

表 3 寿期末停堆后总衰变热计算结果 Table 3 Calculation results of total decay heat after shutdown 时间 Time 裂变产物 Fission products/% 锕系核素 Actinide nuclides/% 活化产物 Activated products/% 衰变热 Decay heat/W 衰变热占比 Decay heat ratio/% 1 s 97.1 2.20 0.75 1.22×105 6.09 1 min 96.1 3.86 0.02 6.85×104 3.43 1 h 94.2 5.84 0.00 2.61×104 1.30 1 d 89.4 10.56 0.00 9.21×103 0.46 30 d 99.98 0.02 0.00 2.19×103 0.11 1 a 99.86 0.14 0.00 1.82×102 0.009 1 50 a 94.6 5.36 0.00 4.86 0.0002

表 3 寿期末停堆后总衰变热计算结果 Table 3 Calculation results of total decay heat after shutdown

对于停堆后数分钟甚至数小时量级的衰变热数据，是作为放射性取样检测等用途的主要参考数据，对于超过1 h后中长时间停堆衰变热数据，是作为余热排出系统设计及排盐罐安全分析所需重点关心的数据。而对于时间超过一年甚至更长时间的衰变热数据，是乏燃料长期贮存以及乏燃料后处理的主要参考数据。

本工作基于Mathematica 7.0建立了MSR主回路系统衰变热流动特性及其分布的数值模拟程序，并与参考程序ORIGENS在静态燃耗下的结果进行了初步验证，二者在全燃耗寿期的计算偏差在±4%范围以内，同时与MSRE实验堆衰变热数据进行了比较，二者偏差在±2.76%范围内，符合较好。对TMSR-LF1正常运行工况及停堆工况衰变热进行了分析。结果表明：正常运行工况下，各区域衰变热约在20 s就已趋平衡，达到平衡态时，堆芯活性区衰变热占总衰变热功率的46.7%，上腔室为31.8%，热管段1#为1.21%，主泵为14.6%，热管段2#为0.89%，换热器为2.21%，冷管段为1.67%，下腔室为0.94%，分析结果及结论可作为MSR主回路系统管道及设备保温设计的参考。

在熔盐堆的工程设计及运行中，为了对主回路系统及设备进行保温系统设计、热工水力安全分析、余热排出设计，必须准确了解主回路系统内的衰变热总量、各区域的分布及随时间的变化特性，建立合理的物理模型对衰变热的准确估算和对反应堆安全设计、事故安全分析及乏燃料储存均具有重要的意义。下一步对熔盐堆衰变热的分析还需更进一步的分析，熔盐堆主回路系统裂变产物核素种类繁多，根据裂变产物的溶解特性可分为三类：惰性气体类、惰性金属类以及易溶解类。其中惰性金属类不易溶于燃料盐，如Nb、Mo、Ru、Sb、Te等元素，根据美国橡树岭国家实验室的MSRE运行经验来看，惰性金属裂变产物会附着在不同材料的交界处，如气液界面、石墨组件表面以及合金与燃料盐交界面，因此这类核素将不会均匀地溶解在主回路系统中，其迁移原理及其分布还需进一步开展相关研究和分析。另外，主回路系统腐蚀活化产物Co、Fe、Cr、Mn、Ni等长寿命放射性核素在系统中的化学形态、演化过程、迁移与沉积对主回路系统衰变热分布的影响及其贡献也是下一步需要进一步研究的内容。