2. 中国科学院大学 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
在过去的几十年中,质子束流被广泛地应用于癌症治疗。上海质子治疗装置(Shanghai Proton Therapy Facility)是中国首台自主研发的医用质子癌症治疗装置,目前正处于总装调试阶段[1-4]。
束配系统是医用质子癌症治疗装置的关键系统之一,其主要目的是将加速器引出束流转换为治疗束流,并将治疗束流准确照射在目标组织上,以满足医生制定的处方剂量率以及三维剂量分布。
束配系统可以划分为被动束配系统[5]和主动束配系统[6]。被动束配系统主要采用散射和降能的方法使加速器引出的质子束流在空间上均匀分布,适形于目标组织。主动束配系统直接采用加速器引出束流照射目标组织,通过扫描磁铁改变束流位置,实现在侧向扩展,并且采用加速器直接调节束流能量,实现在深度方向的扩展。
主动束配系统包括扫描磁铁和电离室等主要硬件,相对于被动束配系统,治疗头结构大为简化。主动束配系统几乎可以完全实现对目标组织的三维适形,同时,主动束配系统束流利用率高,半影区和末端剂量衰减(Distal-Dose Fall Off, DDF)都比较小。上海质子治疗装置中也采用了主动束配系统。
主动束配系统工作方式大致划分为点扫描[7]和连续扫描[8]。点扫描在束流移动阶段停止照射;连续扫描则是在束流移动阶段保持照射。上海质子治疗装置采用点扫描治疗模式,其束配系统的工作流程如下:
1) 通过改变扫描磁铁的设定电流值来移动束流到达指定照射位置;2)打开束流进行照射;3)当该照射点的粒子数到达治疗计划系统(Treatment Planning System, TPS)指定的粒子数后,关闭束流;4)移动束流到下一个照射点的指定位置。
主要的临床治疗参数如表 1所示。
| 表 1 主要临床治疗技术参数 Table 1 Main therapy technical parameters |
照射位置控制系统是质子治疗装置重要的组成部分,质子束流垂直入射进入治疗头,经过扫描磁铁的偏转,照射到患者的肿瘤区域。照射位置控制系统的功能是对束流的偏转进行精确控制,使得束流在等中心平面上的照射位置尽可能地接近TPS的设定值。
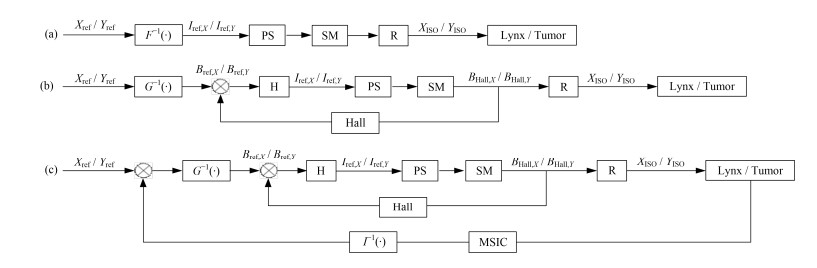
最基本的照射位置控制系统的控制原理如图 1(a)所示,其采用的是前馈控制。图 1(a)中SM表示安装在治疗头内部的用于偏转质子束流的扫描磁铁;PS表示用于驱动扫描磁铁的扫描电源;Lynx表示放置在等中心处用于测量束流位置的IBA荧光靶探测器;(Xref, Yref)为治疗计划系统给出的在等中心平面上每个照射点位置坐标的设定值;(XISO, YISO)为束流在等中心平面上的实际位置坐标;(Iref, X, Iref, Y)为扫描电源励磁电流的设定值;R为束流经过扫描磁铁后发生偏转的传递矩阵。
|
图 1 照射位置控制系统的控制原理 Figure 1 Controlling strategy of the scanning position control system |
在实际治疗前,首先通过离线测量的方式对扫描电源励磁电流的设定值和在等中心处束流的照射位置进行标定,其映射关系为:
| $ \left( {{X}_{\text{ISO}}}, {{Y}_{\text{ISO}}} \right)\text{=}F\left( {{I}_{\text{ref, }X}}, {{I}_{\text{ref, }Y}} \right) $ | (1) |
该映射关系的逆映射记为F-1,利用该逆映射关系,能够根据每个照射点位置坐标的设定值(Xref, Yref)计算出扫描电源励磁电流的设定值(Iref, X, Iref, Y)。
上述基于前馈控制的照射束流位置控制方法的最大问题在于:由于扫描磁铁存在磁滞效应,无法实现扫描磁场的精确控制。
日本三菱公司设计了如图 1(b)所示的照射束流位置反馈控制系统[9-10]。该系统相比于前者最大的区别在于其在位于扫描磁铁中心位置的真空盒外侧安装了用于测量磁感应强度的霍尔探头(Hall),并采用反馈控制的方式来对扫描磁铁的励磁电流进行控制,图 1(b)中(BHall, X, BHall, Y)为霍尔探头测得的磁感应强度。由于在等中心处的束流位置与在质子束流运动路径上的积分磁场的大小具有一一对应的关系,同时在扫描磁铁中心位置测得的磁感应强度与该积分磁场的大小具有一一对应的关系,因此可以得到在等中心处的束流位置与霍尔探头测得的磁感应强度的映射关系,有:
| $ \left( {{X}_{\text{ISO}}}, {{Y}_{\text{ISO}}} \right)\text{=}G\left( {{B}_{\text{Hall, }X}}, {{B}_{\text{Hall, }Y}} \right) $ | (2) |
该映射关系的逆映射记为G-1。通过该逆映射,我们能够根据每个照射点位置坐标的设定值(Xref, Yref)计算出霍尔探头测得的磁感应强度的设定值(Bref, X, Bref, Y)。通过调整扫描电源励磁电流,使得磁感应强度的测量值和设定值相等,以此来实现更为精确的束流位置控制。
然而,上述基于霍尔探头测量磁感应强度的照射位置反馈系统仍存在实际治疗期间无法对质子束流的位置进行实时的测量和校正的不足。
Scandurra等[11]的研究表明,在真空盒外侧安装的位置电离室测得的束流位置与在等中心处的束流位置存在一一对应关系。因此可以通过在治疗头内部安装位置电离室的方式来实时地计算出束流在等中心处位置,并通过调整扫描磁铁励磁电流的设定值来对质子束流进行校正。
上海质子治疗装置照射位置控制系统的结构框图如图 1(c)所示。图 1(c)中(XIon, YIon)为位置电离室测得的束流位置。在实际治疗前,首先对位置电离室测得的束流位置与在等中心处的束流位置进行标定,找出其映射关系:
| $ \left( {{X}_{\text{ISO}}}, {{Y}_{\text{ISO}}} \right)\text{=}I\left( {{X}_{\text{Ion}}}, {{Y}_{\text{Ion}}} \right) $ | (3) |
该映射关系的逆映射记为I-1,通过该逆映射,能够根据位置电离室测得的束流位置(XIon, YIon)计算出束流在等中心处的位置(XISO, YISO)。通过对比(XISO, YISO)和(Xref, Yref)的差值,来对质子束流位置进行校正。
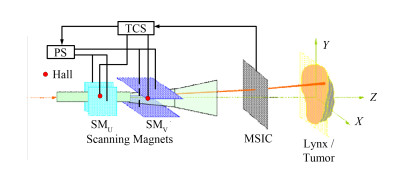
2 主要硬件设备上海质子治疗装置的照射位置控制系统的硬件结构主要包括:安装在治疗头内部的用于偏转质子束流的扫描磁铁、用于驱动扫描磁铁的扫描电源、用于测量束流位置的条带位置电离室、用于测量磁感应强度的霍尔探头、用于进行控制的治疗控制系统、以及放置在等中心处用于测量束流位置的荧光靶探测器(IBA Lynx),硬件结构如图 2所示。
|
图 2 照射位置控制系统硬件结构 Figure 2 Hardware of the scanning position control system |
扫描磁铁的用途是使质子束流发生偏转,使之能够准确地照射到目标照射位置。表 2是扫描磁铁的主要性能指标。
| 表 2 扫描磁铁设计参数 Table 2 Specifications of scanning magnets |
为满足剂量率的要求,通过采用电源部件参数和控制参数匹配来降低扫描电源的调整时间。由于需要双向输出,主功率回路采用正负推挽结构。通过采用两级结构,实现了电源的纹波抑制和调节速度。前级进行整流和稳压,后级输出双向电流。表 3是扫描电源的主要性能指标。
| 表 3 扫描电源设计参数 Table 3 Specifications of the scanning power supply |
为了能够准确地测得扫描磁铁的磁感应强度,在扫描磁铁中心处位于真空盒的外侧各安装了一个瑞士SENIS公司型号为I1A-0YA05F-J02T2K5J的霍尔探头。
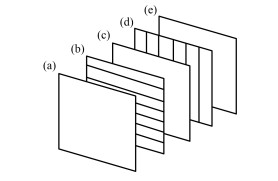
2.4 位置电离室位置测量电离室是扫描治疗头的核心设备,其测量精度和分辨率直接影响到照射剂量分布的精度。上海质子治疗装置采用了自主研发的条带平板电离室(Multi-Strip Ionization Chamber, MSIC)作为位置电离室[12]。其工作原理是将信号引出电极分割成平行的条带,通过测量不同条带的输出电荷得到束流位置,工作气体为自由空气。电离室的结构示意图如图 3所示,其采用5层膜的结构,其中第3层(c)为高压膜,第一层(a)和第5层(e)为屏蔽膜(与地线连通),第二层(b)与第4层(d)为信号膜,分别用于测量U和V方向的束流位置。图 4是位置电离室的实物图。
|
图 3 位置测量电离室结构示意图 Figure 3 Schematic diagram of the position monitor ion chamber |

|
图 4 位置测量电离室实物图 Figure 4 Photo of position monitor ion chamber |
位置测量电离室的设计参数如下:位置测量精度为±0.5 mm,位置测量分辨率为±0.2 mm (2θ),数据率为1.667 kHz,离子收集时间为70 μs。
为满足质子调强治疗(Intensity-Modulated Proton Therapy, IMPT)对剂量控制精度的要求,电离室电子学需要提高测量分辨率,我们采用集成化的多路电流模数转换器(Current ADC)来提高位置电离室电子学的测量信噪比,并且采用了抗辐照器件。
2.5 荧光靶位置电离室为了对等中心平面上的束流位置进行测试和标定,在等中心处放置了由比利时的IBA公司设计生产的Lynx荧光靶探测器(图 5),其束流位置分辨率为±0.5 mm。

|
图 5 荧光靶探测器 Figure 5 Fluorescent detector (IBA Lynx) |
上海质子治疗装置的照射位置控制系统主要通过:1)在等中心处的束流位置与霍尔探头测得磁感应强度之间的映射算法;2)位置电离室测得的束流位置与在等中心处的质子束流的横向位置之间的映射算法;3)基于前馈的磁滞补偿算法;4)照射位置校正算法来实现束流位置的精确控制。
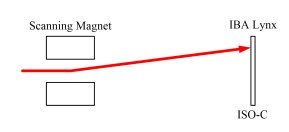
3.1 “等中心处束流位置–扫描磁铁磁场强度”的映射关系霍尔探头测得的磁感应强度与等中心处束流位置(ISO center, ISO-C)之间的映射关系示意图如图 6所示,等中心处的束流位置通过荧光靶探测器(IBA Lynx)测得。
|
图 6 扫描磁铁磁感应强度与等中心处束流位置间的映射关系 Figure 6 Mapping between magnetic field of scanning magnets and spot position at ISO center |
通过多项式拟合算法来对上述映射关系进行标定,其表达式如下:
| $ \left\{ \begin{align} &{{f}_{\text{B, U}}}(x, y)={{a}_{0}}+{{a}_{1}}x+{{a}_{2}}y+{{a}_{3}}{{x}^{2}}+{{a}_{4}}xy+{{a}_{5}}{{y}^{2}} \\ &{{f}_{\text{B, V}}}(x, y)={{b}_{0}}+{{b}_{1}}x+{{b}_{2}}y+{{b}_{3}}{{x}^{2}}+{{b}_{4}}xy+{{b}_{5}}{{y}^{2}} \\ \end{align} \right. $ | (5) |
式中:fB, U(x, y)和fB, V(x, y)表示在两块扫描磁铁中心处霍尔探头测得的磁感应强度;x和y分别表示在等中心处荧光靶探测器测得的束流位置坐标;a0, a1, a2, …, b0, b1, b2, …为待拟合的系数。假设一共测得n组数据,矩阵的表达式如下:
| $ \overbrace{\left[\begin{matrix} 1&{{x}_{0}}&x_{0}^{2}&{{y}_{0}}&y_{0}^{2}&{{x}_{0}}{{y}_{0}} \\ 1&{{x}_{1}}&x_{1}^{2}&{{y}_{1}}&y_{1}^{2}&{{x}_{1}}{{y}_{1}} \\ \vdots &\vdots &\vdots &\vdots &\vdots &\vdots \\ 1&{{x}_{n}}&x_{n}^{2}&{{y}_{n}}&y_{n}^{2}&{{x}_{n}}{{y}_{n}} \\ \end{matrix} \right]}^{{{\mathit{\boldsymbol{A}}}_{\text{carib}}}}\overbrace{\left[\begin{matrix} {{a}_{0}}&{{b}_{0}} \\ {{a}_{1}}&{{b}_{1}} \\ \vdots &\vdots \\ {{a}_{5}}&{{b}_{5}} \\ \end{matrix} \right]}^{{{\mathit{\boldsymbol{x}}}_{c}}}=\overbrace{\left[\begin{matrix} {{B}_{x0}}&{{B}_{y0}} \\ {{B}_{x1}}&{{B}_{y1}} \\ \vdots &\vdots \\ {{B}_{xn}}&{{B}_{yn}} \\ \end{matrix} \right]}^{{{\mathit{\boldsymbol{B}}}_{\text{carib}}}} $ | (6) |
| $ {{\mathit{\boldsymbol{A}}}_{\text{carib}}}{{\mathit{\boldsymbol{x}}}_{c}}={{\mathit{\boldsymbol{B}}}_{\text{carib}}} $ | (7) |
计算系数矩阵xc通过最小二乘法计算得出:
| $ {{\mathit{\boldsymbol{x}}}_{c}}={{\left( \mathit{\boldsymbol{A}}_{\text{carib}}^{\text{T}}{{\mathit{\boldsymbol{A}}}_{\text{carib}}} \right)}^{-1}}\mathit{\boldsymbol{A}}_{\text{carib}}^{\text{T}}{{\mathit{\boldsymbol{B}}}_{\text{carib}}} $ | (8) |
式中:上标T表示转置矩阵。
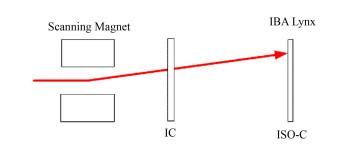
3.2 “等中心处的束流位置–位置电离室测得的束流位置”的映射关系在等中心平面上的束流位置与位置电离室(Ion Chamber, IC)测得的束流位置间的映射关系如图 7所示,我们通过平滑薄板样条曲线(Smoothed Thin-Plate Splines)[13]对其映射关系进行标定。
|
图 7 等中心处的束流位置与位置电离室测得的束流位置间的映射关系 Figure 7 Mapping between spot position at ISO center and at ion chamber |
假设一共测得m组数据,其中第i组数据的束流在等中心平面内的位置坐标为xISO, i=(xISO, i, yISO, i),其所对应的位置电离室测得的束流位置坐标为xION, i=(xION, i, yION, i)。上述映射关系可以表示为:
| $ \begin{align} &{{f}_{\text{ISO, }X}}\left( \mathit{\boldsymbol{x}} \right)=\sum\limits_{i=1}^{m}{{{a}_{1i}}G\left( {{\mathit{\boldsymbol{x}}}_{\text{ION}}}, {{\mathit{\boldsymbol{x}}}_{\text{ION, }i}} \right)}+{{b}_{11}}+{{b}_{12}}{{x}_{\text{ION}}}+{{b}_{13}}{{y}_{\text{ION}}} \\ &{{f}_{\text{ISO, }Y}}\left( \mathit{\boldsymbol{x}} \right)=\sum\limits_{i=1}^{m}{{{a}_{2i}}G\left( {{\mathit{\boldsymbol{x}}}_{\text{ION}}}, {{\mathit{\boldsymbol{x}}}_{\text{ION, }i}} \right)}+{{b}_{21}}+{{b}_{22}}{{x}_{\text{ION}}}+{{b}_{23}}{{y}_{\text{ION}}} \\ \end{align} $ | (9) |
其中,待定系数为a=[a1 a2 … am]T,b=[b1 b2 b3],其可以通过如下方式进行求解:
| $ \mathit{\boldsymbol{b}}={{\left( {{N}^{\text{T}}}{{M}^{-1}}N \right)}^{-1}}{{N}^{\text{T}}}{{M}^{-1}}\mathit{\boldsymbol{y}} $ | (10) |
| $ \mathit{\boldsymbol{a}}={{M}^{-1}}\left( \mathit{\boldsymbol{y}}-N\mathit{\boldsymbol{b}} \right) $ | (11) |
其中,p为平滑因子:
| $ M=\left[\begin{matrix} G\left( {{\mathit{\boldsymbol{x}}}_{1}}, {{\mathit{\boldsymbol{x}}}_{1}} \right)&G\left( {{\mathit{\boldsymbol{x}}}_{1}}, {{\mathit{\boldsymbol{x}}}_{2}} \right)&\cdots &G\left( {{\mathit{\boldsymbol{x}}}_{1}}, {{\mathit{\boldsymbol{x}}}_{m}} \right) \\ G\left( {{\mathit{\boldsymbol{x}}}_{2}}, {{\mathit{\boldsymbol{x}}}_{1}} \right)&G\left( {{\mathit{\boldsymbol{x}}}_{2}}, {{\mathit{\boldsymbol{x}}}_{2}} \right)&\cdots &G\left( {{\mathit{\boldsymbol{x}}}_{2}}, {{\mathit{\boldsymbol{x}}}_{m}} \right) \\ \vdots &\vdots &\ddots &\vdots \\ G\left( {{\mathit{\boldsymbol{x}}}_{m}}, {{\mathit{\boldsymbol{x}}}_{1}} \right)&G\left( {{\mathit{\boldsymbol{x}}}_{m}}, {{\mathit{\boldsymbol{x}}}_{2}} \right)&\cdots &G\left( {{\mathit{\boldsymbol{x}}}_{m}}, {{\mathit{\boldsymbol{x}}}_{m}} \right) \\ \end{matrix} \right]+pI $ | (12) |
| $ N=\left[\begin{matrix} 1&{{\mathit{\boldsymbol{x}}}_{1}} \\ 1&{{\mathit{\boldsymbol{x}}}_{2}} \\ \vdots &\vdots \\ 1&{{\mathit{\boldsymbol{x}}}_{m}} \\ \end{matrix} \right] $ | (13) |
| $ G\left( r \right)=\left\{ \begin{array}{*{35}{l}} {{c}_{0}}{{r}^{2}}\ln r,&n=2 \\ {{c}_{1}}r,&n=3 \\ \end{array} \right. $ | (14) |
其中:
由于扫描磁铁并不完全工作在线性区域,并且由于磁滞效应的存在,扫描磁铁的磁场强度和输入的励磁电流的大小为与历史相关的非线性关系。为实现对磁场强度的精确控制,我们设计了一种基于前馈的扫描磁铁磁滞补偿算法[14],测试结果表明:该前馈控制算法能够保证由于磁滞所造成的在等中心处的束流位置偏差控制在±0.07 mm以内。
3.4 照射位置校正算法照射位置控制系统通过计算前一个照射点在等中心平面上的照射位置偏差来对下一个照射点的照射位置的设定值进行修正。对于第i个照射点,束流的入射位置偏差、入射角度偏差等因素导致的束流在等中心处的位置偏差为(ΔXISO, i, ΔYISO, i)。对于第i+1个照射点,其照射位置坐标的设定值(X'ref, i+1, Y'ref, i+1)采用式(15)进行修正:
| $ \left\{ \begin{align} &{{{{X}'}}_{\text{ref}, i+1}}={{X}_{\text{ref}, i+1}}-{{X}_{\text{ISO, }i}} \\ &{{{{Y}'}}_{\text{ref}, i+1}}={{Y}_{\text{ref}, i+1}}-{{Y}_{\text{ISO, }i}} \\ \end{align} \right. $ | (15) |
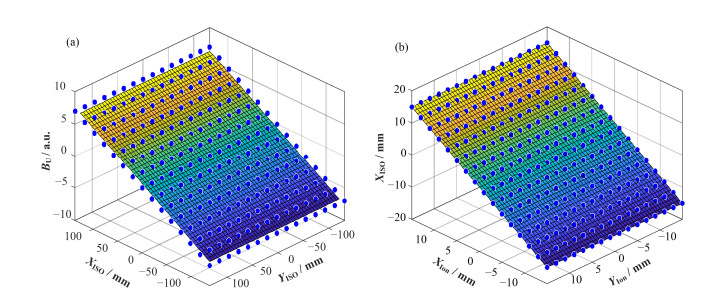
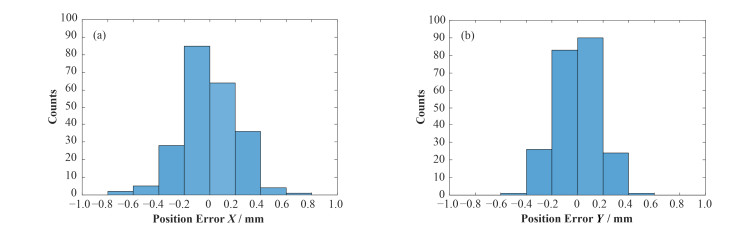
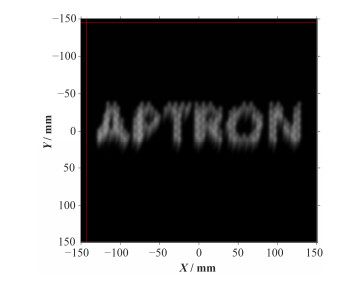
我们采用如下的点阵扫描对上述两种映射关系进行标定:点阵的X方向和Y方向的范围均为-15~15 cm,每个照射点的间距为2 cm。扫描磁铁磁场强度与等中心处束流位置之间以及等中心处的束流位置与位置电离室测得的束流位置之间映射关系的拟合结果分别如图 8(a)、(b)所示。束流在等中心平面上X方向和Y方向位置偏差的分布如图 9所示,位置偏差的最大值分别为0.8mm和0.6 mm,标准差均为0.2 mm。图 10是通过该点扫描照射位置控制系统实现的照射图案扫描。
|
图 8 等中心处束流位置与扫描磁铁磁场强度(a)和位置电离室测得的束流位置(b)之间的映射关系 Figure 8 Relationship between the beam position of the center and the magnetic field intensity of the scanning magnet (a), the beam position measured by the position ionization chamber (b) |
|
图 9 X (a)和Y (b)方向的照射位置误差 Figure 9 Position error in X (a) and Y (b) direction |
|
图 10 上海质子治疗装置logo的点扫描图案 Figure 10 Spot scanning figure of the APTRON logo |
上海质子治疗装置的点扫描照射位置控制系统通过曲面拟合的方法得到了扫描磁场强度与位置电离室读出、扫描磁场强度与等中心束流位置之间的映射关系,并采用了基于前馈的扫描磁铁励磁电流控制方法。在实际治疗时,照射点的位置能够通过比较位置电离室读出与目标位置之间的偏差来进行校正。带束测试表明:束流的照射位置偏差能够控制在±0.2 mm (2σ)以内。该点扫描照射位置控制系统能够实现准确的点扫描照射,满足了照射位置控制的设计要求。
致谢 感谢电源技术部的李瑞和欧阳联华研究员在扫描磁铁以及扫描磁铁电源方面所做的工作。| [1] |
缪亚运, 谷鸣, 陈志豪, 等. 质子治疗装置脉冲电源研制[J]. 核技术, 2016, 39(4): 040401. MIAO Yayun, GU Ming, CHEN Zhihao, et al. Development of pulsed power supply in proton therapy[J]. Nuclear Techniques, 2016, 39(4): 040401. DOI:10.11889/j.0253-3219.2016.hjs.39.040401 |
| [2] |
贾亚军, 李永江, 张潇, 等. 质子治疗中点扫描照射技术的仿真模拟[J]. 核技术, 2016, 39(9): 090202. JIA Yajun, LI Yongjiang, ZHANG Xiao, et al. Simulation of spot scanning in proton therapy[J]. Nuclear Techniques, 2016, 39(9): 090202. DOI:10.11889/j.0253-3219.2016.hjs.39.090202.hjs.39.090202 |
| [3] |
童金, 谷鸣, 袁启兵, 等. 基于FPGA和DDS的质子同步加速器共振慢引出信号源设计[J]. 核技术, 2014, 37(4): 040102. TONG Jin, GU Ming, YUAN Qibing, et al. Design of slow-extraction signal source within proton-synchrotron based on FPGA&DDS[J]. Nuclear Techniques, 2014, 37(4): 040102. DOI:10.11889/j.0253-3219.2014.hjs.37.040102 |
| [4] |
杨朝霞, 李德明, 张满洲, 等. 基于Geant4模拟的质子治疗束配系统的束流光学设计[J]. 核技术, 2013, 36(7): 070201. YANG Zhaoxia, LI Deming, ZHANG Manzhou, et al. Optics design of beam for proton therapy gantry based on Geant4[J]. Nuclear Techniques, 2013, 36(7): 070201. DOI:10.11889/j.0253-3219.2013.hjs.36.070201 |
| [5] |
Yeung D, Palta J. Passive scattering[M]. Berlin Heidelberg: Springer, 2013.
|
| [6] |
Kanai T, Kawachi K, Matsuzawa H, et al. Three-dimensional beam scanning for proton therapy[J]. Nuclear Instruments & Methods in Physics Research, 1983, 214(2): 491-496. |
| [7] |
Pedroni E, Bacher R, Blattmann H, et al. The 200-MeV proton therapy project at the Paul Scherrer Institute:conceptual design and practical realization[J]. Medical Physics, 1995, 22(1): 37. DOI:10.1118/1.597522 |
| [8] |
Furukawa T, Inaniwa T, Sato S, et al. Design study of a raster scanning system for moving target irradiation in heavy-ion radiotherapy[J]. Medical Physics, 2007, 34(3): 1085-1097. DOI:10.1118/1.2558213 |
| [9] |
岩田高明. 粒子射线照射装置[P]. 中国: CN 102414759 B, 2014. YANTIAN Gaoming. Particle beam scanning irradiation system[P]. China: CN 102414759 B, 2014. |
| [10] |
岩田高明. 粒子射线照射装置、粒子射线治疗装置及粒子射线照射方法]P]: 中国: CN 102470255 B, 2014. YANTIAN Gaoming. Particle beam irradiation apparatus, particle beam therapy system and particle beam irradiation methods[P]. China: CN 102470255 B, 2014. |
| [11] |
Scandurra D, Albertini F, R van der Meer, et al. Assessing the quality of proton PBS treatment delivery using machine log files:comprehensive analysis of clinical treatments delivered at PSI Gantry 2[J]. Physics in Medicine & Biology, 2016, 61(3): 1171-1181. |
| [12] |
Zhao B Q, Zhao M H, Liu M, et al. The front-end electronics design of dose monitors for beam delivery system of Shanghai Advanced Proton Therapy Facility[J]. Nuclear Science and Techniques, 2017, 28(6): 63-69. DOI:10.1007/s41365-017-0230-y |
| [13] |
Schmid S, Jiang X, Schäfers K. High-precision lens distortion correction using smoothed thin plate splines[J]. Computer Analysis of Images and Patterns, 2013, 8048: 432-439. DOI:10.1007/978-3-642-40246-3 |
| [14] |
Miao C H, Liu M, Yin C X, et al. Precise magnetic field control of the scanning magnets for the APTRON beam delivery system[J]. Nuclear Science and Techniques, 2017, 28(6): 54-58. DOI:10.1007/s41365-017-0324-6 |


