计算流体力学(Computational Fluid Dynamics, CFD)在核燃料组件流动分析中有着非常广泛的应用,但由于CFD计算受到网格、湍流模型、差分格式、边界条件等多种因素的影响,CFD的计算结果呈现明显的用户效应[1]。棒束因其致密的几何结构以及定位格架的复杂性,给CFD分析带来了挑战,而且在棒束单相流动CFD的分析研究中,尚无统一认可的分析方法,CFD分析结果可信度存在质疑;并且真实的物理情景包含了大量的不确定性,这些不确定性会对结果的可信度带来挑战[2-3],针对CFD的验证确认工作也一直是国内外的研究热点。Conner[4]和Lascar[5]在西屋公司的验证试验中分别使用了RNG k-ε模型和可实现的湍流模型(Realizable k-ε model, RKE)模型对5×5棒束试验进行验证,认为RNG模型对流动曲率及旋转更敏感,并且RKE模型对于格架模拟更为适合。为了确保CFD在单相棒束流动分析中能够得到高置信度的模拟结果,国际上开展了一系列实验作为基准算题。其中包括经济合作组织核能机构(The Nuclear Energy Agency of the Organization for Economic Co-operation and Development, OECD/NEA)组织的MATiS-H棒束验证试验[6-7]与美国电力研究协会(Electric Power Research Institute, EPRI)组织的NESTOR棒束验证试验[8]等。Conner[9]利用二阶非线性湍流模型(Quadratic k-ε model, QKE)分析NESTOR试验,得到了较好的结果。为进一步改进单相棒束流动传热分析的CFD分析方法,完善单相棒束流动传热CFD分析的最佳实践导则,国际原子能机构(International Atomic Energy Agency, IAEA)基于韩国原子能研究院(Korea Atomic Energy Research Institute, KAERI)完成的4×4棒束的流动与传热实验,组织了一个国际基准算题[10]。本文基于KAERI的4×4棒束流动试验展开棒束单相流动的最佳实践方法研究,随后利用敏感性系数法着重分析壁面函数中
CFD模拟值与真实值的偏差被称为误差,但是真实值是未知的,一般用一个区间加上一定的可信度来估计真实值的范围,量化CFD的不确定性便是估计模拟值偏离真实值的程度。CFD误差来源一般可分为三类:数值误差、模型误差以及试验误差[11]。
数值误差包含截断误差、迭代误差以及离散误差。在采用二阶以上精度时,与离散误差相比,截断误差以及迭代误差非常小,因此在考虑数值误差时主要针对离散误差;模拟值与直接数值模拟(Direct Numerical Simulation, DNS)的差便是模型误差,目前重点关注输入参数带来的不确定分析;目前对CFD结果的验证主要是通过与试验结果的比较进行,但是试验结果受到试验段加工水平、安装、实验条件控制以及测量仪器精度等的影响,不可避免地引入一些误差,在对CFD结果进行确认的过程里需要考虑试验误差的影响。本文主要研究数值不确定性以及输入参数的不确定性对结果影响。
1.1 数值不确定性可用网格收敛系数法(Grid Convergence Index, GCI)来估计数值不确定性,假设精确解为fexact,离散值f即为模拟结果,模拟值与精确解的差ε为误差。对离散解误差的估计通常是用Richardson[12]外推法进行,Richardson假设离散解是其精确解与离散步长的幂级数之和:
| $ f={{f}_{{\rm exact}}}+{{g}_{1}}h+{{g}_{2}}{{h}^{2}}+{{g}_{3}}{{h}^{3}}+\cdots $ | (1) |
式中:gi是与离散方式无关的量;h代表网格的特征长度;对于非结构化网格,h可定义为:
| $ h={{\left( \sum\limits_{i=1}^{N}{\Delta {{V}_{i}}}/N \right)}^{1/3}} $ | (2) |
式中:ΔVi代表每个网格的体积;N为网格数量。对于采用二阶精度的计算方式,式(1)中g1为0,从而GCI可定义为:
| $ {\rm GCI}={{F}_{{\rm s}}}\frac{\left| e \right|}{{{r}^{2}}-1} $ | (3) |
式中:r指不同网格特征尺度的比值;Fs为安全系数;两套网格推荐值为3,三套网格推荐值为1.25。e为不同网格计算结果的相对差异,定义如下:
| $ e={{f}_{2}}-{{f}_{1}} $ | (4) |
GCI方法不仅考虑了计算结果的相对差异,而且考虑到了二阶精度对计算结果的影响,有更强的借鉴意义。数值不确定性(unum)可定义如下:
| $ {{u}_{{\rm num}}}=\frac{{\rm GCI}}{2} $ | (5) |
可将输入参数的不确定性(uinput)看做模拟结果(S)在与其相关的自变量(Xi)的泰勒展开,略去高阶项可写为:
| $ {{u}^{2}}_{{\rm input}}={{\sum\limits_{i=1}^{n}{\left( \frac{\partial S}{\partial {{X}_{i}}}{{u}_{{{X}_{i}}}} \right)}}^{2}} $ | (6) |
式中:S为计算结果;
| $ \begin{align} & \frac{\partial S}{\partial {{X}_{i}}}=\frac{S\left( {{X}_{1}}, {{X}_{2}}\cdots {{X}_{i}}+\Delta {{X}_{i}}\cdots {{X}_{n}} \right)-S\left( {{X}_{1}}, {{X}_{2}}\cdots {{X}_{i}}-\Delta X\cdots {{X}_{n}} \right)}{2\Delta {{X}_{i}}}+ \\ & \ \ \ \ \ \ \ \ o\left( \Delta {{X}^{2}}_{i} \right) \\ \end{align} $ | (7) |
求出数值不确定性以及输入参数的不确定性,那么棒束单相CFD不确定性可定义为:
| $ {{u}_{{\rm val}}}=\sqrt{{{u}^{2}}_{{\rm num}}+{{u}^{2}}_{{\rm input}}} $ | (8) |
利用商业CFD软件STAR-CCM+10.02.010进行分析,STAR-CCM+基于其网格划分的灵活性以及湍流模型的多样性,在核工程领域应用愈加广泛。
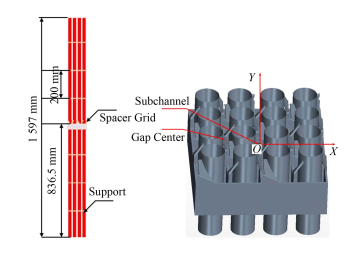
2.1 几何模型图 1展示出CFD计算的几何模型,其尺寸与试验段完全一致。棒束总长为1597 mm,自下而上共有6个支撑格架以及一个搅混格架,相邻两个支撑格架间距为200 mm,搅混格架上表面距离棒束底端距离为836.5 mm,搅混格架高为40 mm。其中棒的直径(D)为25.4 mm,棒间距(P)为34.3 mm,棒间距与棒直径比例(P/D)为1.35。试验的坐标系如图 1所示,以搅混格架上表面为基准平面,以该平面的中心为坐标原点,X、Y的方向如图 1所示,Z的正方向为向上。
|
图 1 几何模型 (a)计算模型,(b)坐标系 Figure 1 Diagram of the geometry model (a) Simulation model, (b) Coordinated system |
高质量的网格是保证计算精确度的关键,因此最佳实践方法需要得到网格无关解。然而几何模型对网格的质量有较大影响,所以生成网格前需对几何进行检验,防止出现点接触以及线接触。同时根据几何复杂程度可将几何分成两部分:带有结构相对复杂的搅混格架部分以及有结构相对简单的棒束支架部分。支架间是光棒区,可以通过拉伸的方式生成结构完全相同的网格,对于搅混格架部分需进行更多的局部设置。这样进行网格划分可以减少对计算机内存需求并且可以节约时间。本文选用了切割体网格,因为切割体网格兼具结构化网格质量高与非结构化网格适应性好的特点,对于棒束结构有着较好的适用性。为研究棒束CFD计算对网格的需求,流动计算分别选择了三种不同网格进行比较,其中网格参数如表 1所示。
| 表 1 网格参数 Table 1 Mesh parameters |
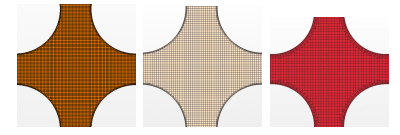
图 2为计算所用的网格。为了边界网格向中心区域更好的过度,其伸展率设置为1.1。壁面Y+在15-58。
|
图 2 不同网格 (a)网格1,(b)网格2,(c)网格3 Figure 2 Different local meshes (a) Mesh 1, (b) Mesh 2, (c) Mesh 3 |
本文选择了在工程领域较常用的三种两方程模型,分别是标准k-ε模型、可实现的k-ε模型以及二阶非线性k-ε模型。其中RKE模型改进了湍流粘性,将流动的曲率以及旋转考虑了进去;方程变化较大,在剪切流、自由流、分离流以及混合流中应用较为广泛。QKE模型考虑了非线性产生项,对于几何结构较为复杂的流动较为适用。在模拟计算中入口采用的是均匀流速入口,其值为1.5 m·s-1,环境温度为35 ℃,出口边界为压力出口,其值设置为0。
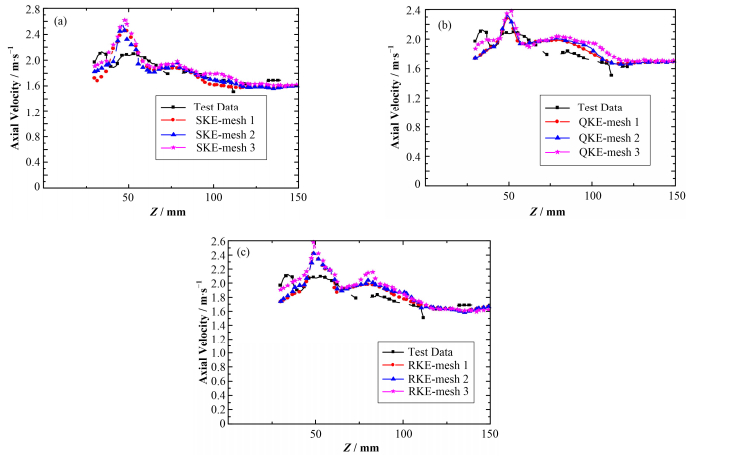
2.4 网格敏感性分析图 3展示了不同网格下各湍流模型对子通道间轴向速度的模拟结果,随着网格数量的增加,在三种模型下,与网格3相比,网格2与网格1的计算结果吻合较好,其最大偏差小于4.7%。可以认为,当网格数量达到1.2亿时,此时计算结果已与网格无关,下文将以网格1的计算结果进行说明。
|
图 3 不同网格下SKE模型(a)、QKE模型(b)、RKE模型(c)的结果比较 Figure 3 Comparison of axial velocity of SKE model (a), QKE model (b), RKE model (c) in different meshes |
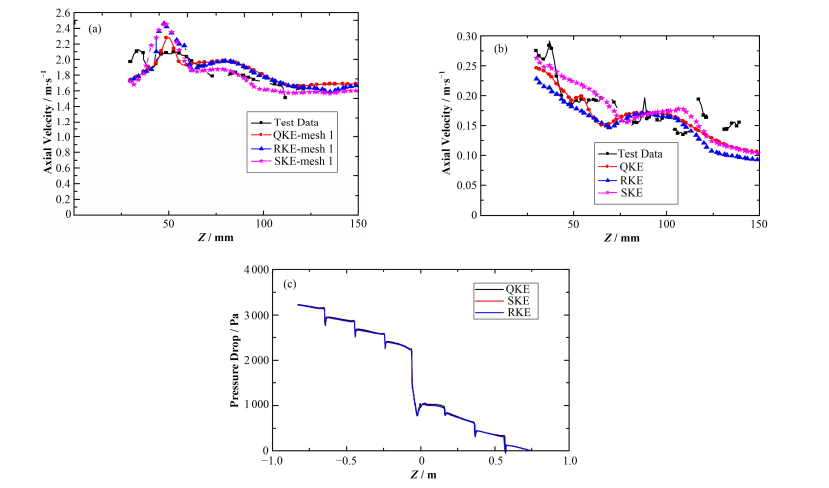
图 4分别展示出不同湍流模型在网格1下对棒间中心通道轴向速度以及轴向速度脉动的比较结果。轴向速度方面,在定位格架下游约50 mm处,三种湍流模型均预测出速度峰值,SKE、RKE和QKE模型预测峰值分别高出试验值约25%、22%和12%,相比之下,QKE模型预测值更加准确。并且定位格架下游120 mm之后,轴向速度趋于稳定,QKE预测值更符合试验值。
|
图 4 三种模型的轴向速度(a)、轴向RMS速度(b)以及压降(c)的结果比较 Figure 4 Comparison of axial velocity (a), axial RMS velocity (b) and pressure drop (c) in the three models |
轴向脉动速度(Root Mean Square, RMS)方面,其中试验值由式(9)得到:
| $ {{U}_{{\rm RMS}}}=\sqrt{\frac{\sum\limits_{i=1}^{N}{{{\left( {{u}_{i}}-{{u}_{{\rm mean}}} \right)}^{2}}}}{N-1}} $ | (9) |
式中:ui为每一次测量得到的速度;umean为平均速度。由于两方程模型不能直接求解出湍流应力,故计算值用
压降预测方面,本文选择了流体域边界的位置,三种模型的预测结果总体来看预测较为一致,最大偏差小于2%,说明在该网格下,对压降的预测较为准确。下文将以QKE模型来进行说明。
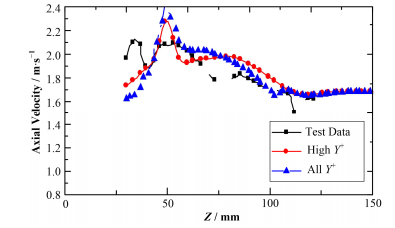
2.6 壁面处理图 5展示了QKE选择不同壁面处理对轴向速度的影响,由于低Y+对网格加密要求较高,带来了较大的计算量,故本文选择了高Y+和所有Y+处理的方法。高Y+指的是湍流模型认为第一层网格处于对数区;所有Y+处理指的是对于较小的网格认为处于粘性底层区,对于较大的网格认为处于对数区,是一种比较流行的模拟过渡区的方法。如图 5所示,两种壁面处理的方式都可以预测轴向速度的变化趋势,所有Y+处理得到的轴向速度波动较大,且过高的估计速度的峰值,此外高Y+的收敛性较好。
|
图 5 不同壁面处理结果比较 Figure 5 Comparison of different wall treatment |
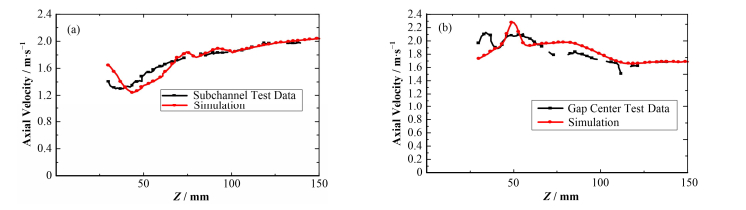
图 6展示出QKE模型可以较好预测轴向速度的变化趋势,与试验值吻合较好。子通道中心轴向速度变化显示出搅混格架对其下游的流场有较大影响,在其下游约50 mm处,轴向速度出现谷值,随着距离搅混格架越远,子通道中心速度逐渐上升慢慢趋于稳定,稳定值约是最低点的1.7倍。棒间中心的轴向速度显示出相反的特征,在搅混格架下游约50 mm处,棒间中心轴向速度出现峰值,随着距离搅混格架愈远速度逐渐降低,并且趋于稳定,其峰值约是稳定值的1.3倍。这是因为搅混翼对来流进行再分配,加大了横向流动,迫使棒间流速升高,随着距离搅混格架越远,其影响作用越来越小,流场逐渐趋于稳定。对比试验值与模拟值,QKE模型会高估轴向速度的峰值。
|
图 6 子通道中心(a)和棒间中心(b)的轴向速度比较 Figure 6 Comparison of axial velocity in subchannel center (a) and gap center (b) |
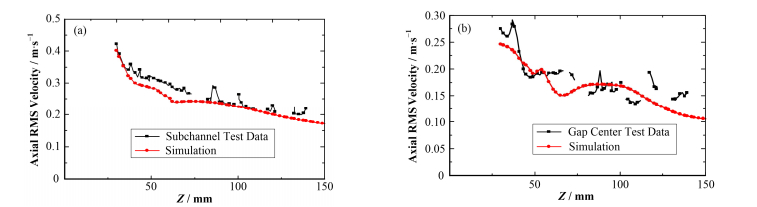
为研究搅混格架对下游横向流动的影响,图 7展示出子通道以及棒间通道的脉动速度,脉动速度本质上反映了湍流的强弱。子通道以及棒间通道显示出搅混格架下游轴向脉动速度随着距搅混格架愈远而慢慢减小,其中子通道中心的脉动速度最大值约是图 7中所示最小值的2.5倍,靠近搅混格架处湍流强度较大,增强了横向流动。棒间中心轴向速度的脉动速度变化较大,Z=50 mm处脉动速度无出现极小值点,且图 6中该处轴向速度出现峰值,说明搅混格架在此处的影响较大。并且,模拟值会低估轴向速度的脉动速度。
|
图 7 子通道中心(a)和棒间中心(b)的脉动速度比较 Figure 7 Comparison of RMS velocity in subchannel center (a) and gap center (b) |
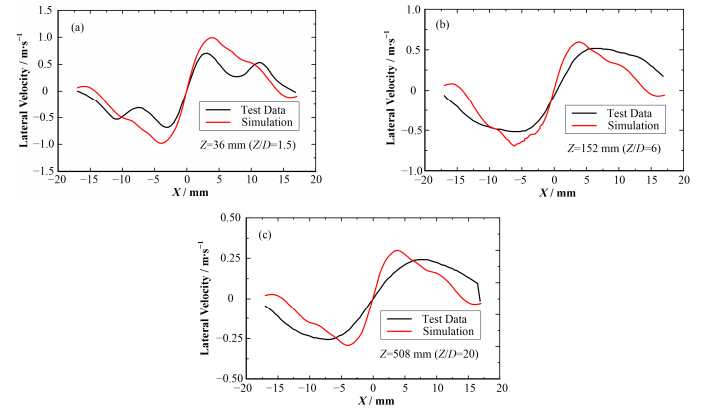
图 8分别展示了搅混格架下游Z=1.5D、Z=6D、Z=20D处的横向速度,总体来看QKE模型值均能捕捉到横向速度的变化趋势,但高估了速度峰值。图 8(a)所示Z=26 mm平面,在X约为-7 mm处试验值出现极大值,模拟结果并未预测到该现象,这是因为此处距搅混格架较近,子通道轴向速度受搅浑翼影响较强,横向流动较为剧烈,由图 6可知,QKE模型高估了该平面处子通道中心的轴向速度,低估该处湍流强度,故预测该处横向速度相比较小,同理预测在X约为14 mm处的横向速度相比较小。比较试验结果,在搅混格架下游不同平面内,横向速度的峰值出现在棒束的切线上;但模拟结果中峰值位置略微提前。在Z=36 mm处横向速度峰值约是Z=508 mm处横向速度峰值3倍,Z=152 mm处横向速度的峰值约是Z=508 mm处横向速度峰值的两倍,说明搅混格架对下游流场的影响渐渐减弱。
|
图 8 Z=26 mm (a)、Z=152 mm (b)、Z=508 mm (c)横向速度比较 Figure 8 Comparison of lateral velocity in Z=26 mm (a), Z=152 mm (b), Z=508 mm (c) |
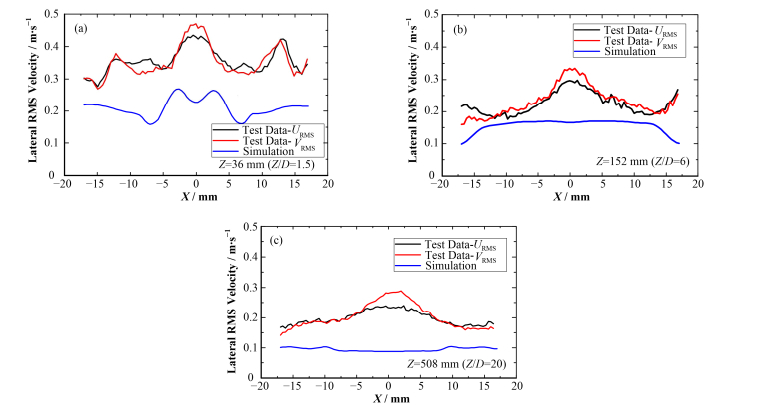
如图 9所示,定位格架下游不同平面内模拟值均会低估横向速度的脉动值,随着距搅混格架愈远,模拟值与试验值差别变大。从试验值来看,X、Y方向的横向脉动速度变化趋势相近,Y方向的横向脉动速度峰值略大。图 8(a)在X约为±14 mm处横向脉动速度出现局部极大值,而模拟值未捕捉到这一现象,这是因为该处在搅混格架下游且距搅混格架较近,受搅混格架影响较大,横向流动加强,横向脉动速度较大,但QKE模型低估了此处的湍流强度。随着距搅混格架愈远模拟得到的脉动幅值逐渐减小,且减小幅度大于试验值,一方面由图 6及图 8可知,随着距离搅混格架愈远,棒间通道轴向速度愈小,流场趋于稳定,且横向速度峰值逐渐减小,导致速度梯度减小,湍动能降低。另一方面图 7中可以看到距搅混格架较近时子通道中心轴向脉动速度的峰值与横向脉动速度相当,而随着远离搅混格架,湍流主要由壁面剪切应力产生,轴向脉动速度减小速度高于横向脉动速度,而涡粘性模型假设流体各向同性,认为三个方向脉动速度相同,这样会使得横向脉动速度模拟值与试验值差别加大。
|
图 9 Z=26 mm (a)、Z=152 mm (b)、Z=508 mm (c)横向脉动速度比较 Figure 9 Comparison of lateral RMS velocity in Z=26 mm (a), Z=152 mm (b), Z=508 mm (c) |
基于上文的讨论,棒束单相流动CFD最佳实践方法可总结如下:
网格划分:对于几何结构较为复杂的定位格架可作适当简化处理,如钢突、弹簧等;并且将几何结构相对规则的光棒区与定位格架分开进行划分网格,光棒区采用拉伸网格可以得到非常规整的网格,定位格架以及壁面需进行适当的加密处理,5层棱柱层是可以取得较好的结果。其中近壁面第一层网格设置为0.1 mm,中心区域网格设置为0.4 mm作为基本尺寸,可以预测出流动的变化趋势,并且CFD计算需要找到网格无关解。
湍流模型及壁面处理:二阶非线性k-ε模型对于棒束流动可以取得较好的模拟结果,可实现的k-ε模型加上所有Y+处理方法可以得到相近的模拟结果;标准k-ε模型预测结果相比较差。高Y+的壁面处理方法可以得到较好的收敛性,并且对网格数量要求相对较少。
出入口边界条件:入口边界设为均匀流速入口,出口边界设置为压力出口可以取得较好的结果。
与试验值比较分析来看,模拟值总体会高估轴向速度的峰值,对横向速度的预测相对更加准确,但会低估轴向以及横向的速度波动。
3 不确定性量化分析上文的讨论已经得出棒束单相流动的最佳实践方法,基于上述已经验证的CFD方法,本文主要尝试分析数值不确定性以及壁面函数中相关系数
对于网格1与网格3,特征长度的比例可以由式(10)得到:
| $ {{r}_{31}}=\frac{{{h}_{3}}}{{{h}_{1}}}=\sqrt[3]{{{N}_{1}}/{{N}_{3}}} $ | (10) |
可得r31为1.51,而e为52.37 Pa,根据式(3)可得:
| $ {\rm GC}{{{\rm I}}_{31}}={{F}_{{\rm s}}}\frac{\left| e \right|}{{{r}^{2}}-1}=50.74 $ | (11) |
利用同样的方法可以得到网格3与网格2以及网格2与网格1的GCI,其结果如表 2所示。
| 表 2 压降计算的GCI Table 2 GCI of pressure drop. |
从保守角度出发,由数值不确定性而产生的压降GCI取113.49 Pa,根据式(5)可以得到由数值误差导致的压降预测结果的不确定性为56.75 Pa。
3.2 壁面函数中近壁面的剪切应力可由式(12)得到:
| $ {{\tau }_{{\rm w}}}=\rho l_{{\rm m}}^{2}{{\left( \frac{{\rm d}u}{{\rm d}y} \right)}^{2}} $ | (12) |
其中:lm为混合长度,可由式(13)得到:
| $ {{l}_{{\rm m}}}=\kappa y $ | (13) |
摩擦压降系数由式(14)得到:
| $ {{C}_{f}}=\left| {{\tau }_{{\rm w}}} \right|/\left( \frac{1}{2}\rho u_{{\rm ref}}^{2} \right) $ | (14) |
式中:uref为参考速度,可以看到随着
| $ \frac{{{\mu }_{t}}}{\mu }=R{{e}_{y}}{{C}_{\mu }}^{1/4}\kappa \left[1-\exp \left(-\frac{R{{e}_{y}}}{{{A}_{\mu }}} \right) \right] $ | (15) |
式中:Cμ为0.09;Aμ为70;
| $ R{{e}_{y}}=\frac{\sqrt{k}y}{\nu } $ | (16) |
式中:k为湍流脉动动能;y为到壁面距离;
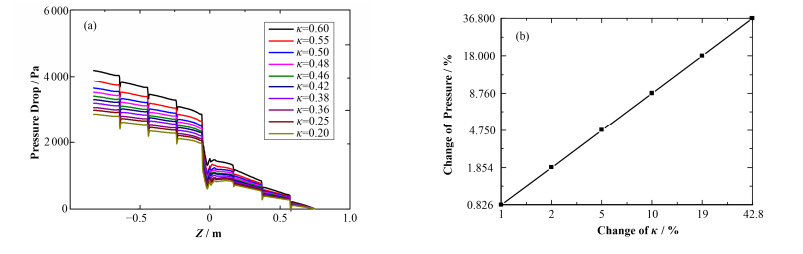
为进一步考察
| $ \frac{\partial S}{\partial \kappa }=\frac{\Delta P}{\Delta \kappa }=4\ 415.85 $ | (17) |
|
图 10 κ值对压降的影响(a)以及κ值变化幅度与压降变化幅度比较(b)[W用2] Figure 10 The effect of κ on the pressure drop (a) and comparison of the change of κ and pressure drop (b) |
对于输入参数的标准差的确定,理想条件下可以基于试验确定,对于无法进行试验确定的参数,更多的做法是通过查阅参数数据库并且参考专家意见进行确定。这里美国机械工程师协会(American Society of Mechanical Engineers, ASME)给出了一个标准,
| $ {{u}_{{\rm input}}}=\kappa \frac{\partial S}{\partial \kappa }\frac{{{u}_{\kappa }}}{\kappa }=92.73 $ | (18) |
最后可得预测压降的不确定性为:
| $ {{u}_{{\rm val}}}=\sqrt{{{u}^{2}}_{{\rm num}}+{{u}^{2}}_{{\rm input}}}=108.72 $ | (19) |
本文首先介绍了CFD不确定性的来源,主要包括数值不确定性、输入参数的不确定性以及实验数据的不确定性,但实验数据不确定性已经超出分析的范畴。重点介绍了数值不确定性以及敏感性系数分析输入参数的不确定性的过程。随后针对目前棒束单相流动CFD缺乏统一模拟方法现状,总结出棒束单相流动CFD的最佳实践方法,在最佳实践方法的基础上,重点分析数值不确定性以及壁面函数中的κ不确定性对压降预测的影响。结果显示:对压降的预测不确定性为3.2%。
| [1] |
董化平, 樊文远, 郭赟. 板状燃料组件流量分配CFD研究与优化[J]. 核技术, 2016, 39(8): 080603. DONG Huaping, FAN Wenyuan, GUO Yun. CFD investigation and optimization on flow distribution of plate-type assembly[J]. Nuclear Techniques, 2016, 39(8): 080603. DOI:10.11889/j.0253-3219.2016.hjs.39.080603 |
| [2] |
Liu C C, Ferng Y M, Shih C K. CFD evaluation of turbulence models for flow simulation of the fuel rod bundle with a spacer assembly[J]. Applied Thermal Engineering, 2012, 40(7): 389-396. |
| [3] |
Eça L, Hoekstra M. A procedure for the estimation of the numerical uncertainty of CFD calculations based on grid refinement studies[M]. Academic Press Professional, Inc, 2014.
|
| [4] |
Conner M E, Baglietto E, Elmahdi A M. CFD methodology and validation for single-phase flow in PWR fuel assemblies[J]. Nuclear Engineering & Design, 2010, 240(9): 2088-2095. |
| [5] |
Lascar C, Pierre M, Goodheart K, et al. Validation of a CFD methodology to predict flow fields within rod bundles with spacer grids[C]. 15th International Topical Meeting on Nuclear Reactor Thermal-Hydraulics, Pisa, Italy, 2013.
|
| [6] |
Lee J R, Kim J, Song C H. Synthesis of the turbulent mixing in a rod bundle with vaned spacer grids based on the OECD-KAERI CFD benchmark exercise[J]. Nuclear Engineering & Design, 2014, 279: 3-18. |
| [7] |
Podila K, Rao Y. CFD modelling of turbulent flows through 5×5 fuel rod bundles with spacer-grids[J]. Annals of Nuclear Energy, 2016, 97: 86-95. DOI:10.1016/j.anucene.2016.07.003 |
| [8] |
Kang S K, Hassan Y A. Computational fluid dynamics (CFD) round robin benchmark for a pressurized water reactor (PWR) rod bundle[J]. Nuclear Engineering & Design, 2016, 301: 204-231. |
| [9] |
Conner M E, Karoutas Z E, Xu Y. Westinghouse CFD modeling and results for EPRI NESTOR CFD round robin exercise of PWR rod bundle testing[C]. 16th International Topical Meeting on Nuclear Reactor Thermal Hydraulics (NURETH-16), Chicago, Illinois, U. S., 2015.
|
| [10] |
Chang S K, Kim S, Song C H. Turbulent mixing in a rod bundle with vaned spacer grids:OECD/NEA-KAERI CFD benchmark exercise test[J]. Nuclear Engineering & Design, 2014, 279: 19-36. |
| [11] |
Fritz F G, Sargent R G, Daum T. Verification and validation of simulation models[J]. Journal of Simulation, 2013, 7(1): 12-24. DOI:10.1057/jos.2012.20 |
| [12] |
Gounand S, Nicolas X, Médale M, et al. A CFD benchmark study with an analysis of Richardson Extrapolation in the presence of a singularity[J]. Review of Scientific Instruments, 2012, 83(83): 55-58. |
| [13] |
Standard for verification and validation in computational fluid dynamics and heat transfer[M]. The American Society of Mechanical Engineers, 2009.
|
