中国科学院钍基熔盐核能系统研究中心研制了一种适用于监测反应堆运行时产生⁸⁵Kr、¹³³Xe等放射性惰性气体的监测装置，并适用于环境中放射性气体的监测。该监测仪利用大体积NaI(Tl)晶体探测γ射线，以分辨核素，测量γ射线的能量窗为0.08-2.5MeV；利用离子注入型硅半导体探测器探测β射线，以得到待测环境中的放射性活度。由于NaI(Tl)晶体对γ射线具有较高的探测效率，因此在探测γ射线方面得到广泛应用。然而，由于NaI(Tl)晶体对不同能量的γ射线存在较大的能量响应差异^[1]，影响测量的准确性，需要对其进行能量响应补偿。能量响应补偿的方法主要有^[2-3]：软件补偿法和硬件补偿法。软件补偿法即能谱加权法，是一种比较先进的方法，但由于其工艺复杂、价格较高等因素，实际应用受限；硬件补偿法即屏蔽法，其操作工艺简单、价格便宜，成为实际补偿中的有效方法。

屏蔽补偿法需要给出屏蔽体的最佳形状和尺寸，利用MCNP (Monte Carlo N Particle Transport Code)软件模拟实际监测仪中NaI(Tl)晶体在不同形状和尺寸屏蔽体下的能量响应，进而给出最佳的补偿方案。

利用NaI(Tl)探测器来测量空气比释动能率${\dot K_{\rm a}}$，而NaI(Tl)探测器的示值对应的是晶体的吸收剂量率${\dot D_{\rm NaI}}$，受该点处粒子注量率ϕ、粒子能量E、质能吸收系数(${{{u}_{\rm en}}}/{\rho }\;$)的影响。如果辐射场中仅存在一种单能的γ射线时，忽略份额较小的轫致辐射的影响，在辐射场中的某处，空气比释动能率${\dot K_{\rm a}}$和空气的吸收剂量率${\dot D_{\rm a}}$基本相等^[4-5]：${\dot K_{\rm a}} \approx {\dot D_{\rm a}}$。但空气比释动能率和晶体吸收剂量率并不相等，二者间的比值为常数：${\dot K_{\rm a}} = {k_i}{\dot D_{\rm NaI}}$，其中k_i为第i种能量射线的空气比释动能率和晶体吸收剂量率比值。如果辐射场中存在多种不同能量的γ射线时，由于晶体对不同能量段γ射线的响应有所不同，空气比释动能率与晶体吸收剂量率的比值并不是一个常数。由于NaI(Tl)晶体对低能γ射线较为敏感，这就造成探测器在低能段出现过响应现象，以致不能准确测量空气的比释动能率。为了使比值k趋近一个定值，需要采取一定的方法进行能量响应补偿。${{{{\dot{K}}}_{\rm a}}}/{\phi }\;$可以通过查询用于光子外照射防护的剂量转换系数ICRP74号报告^[6]得到，单能γ射线的吸收剂量${{{{\dot{D}}}_{\rm NaI}i}}/{\phi }\;$可以利用MCNP软件模拟计算得到^[7-8]，并将结果对¹³⁷Cs的能量响应进行归一化处理，以得到能量响应曲线。文中利用铅屏蔽来进行能响补偿，利用MCNP模拟补偿铅孔在不同尺寸下的能量响应，通过模拟结果选出合适的铅孔尺寸，较好的补偿措施能使各种能量γ射线下的空气比释动能率和NaI(Tl)晶体吸收剂量率比值近似为定值。

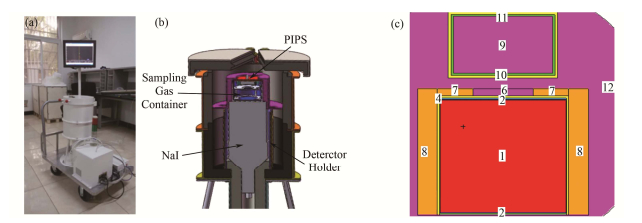
移动式放射性惰性气体监测仪及其探测部分如图 1所示。

图 1

图 1 移动式放射性惰性气体监测仪(a)、探测器部分的剖面图(b)及整体建模图(c) Figure 1 Views of the mobile radioactive gas monitor (a), its detection part (b) and the whole model (c)

根据监测仪实际采用的探测晶体尺寸及气体取样容器的尺寸，利用MCNP进行建模，模型中探测部分：NaI(Tl)晶体尺寸为ø12.7 cm×12.7 cm；晶体外包裹厚度为0.05 cm的MgO反射层；外侧面和前部分别为0.2 cm和0.25 cm的Al壳，底部有机玻璃厚度为0.2 cm，顶部聚乙烯海绵CH₂厚度为0.2cm。气体取样容器部分：容器内径10 cm，高6.4cm；容器由内层的有机玻璃和外层的铝组成，有机玻璃和铝层的厚度分别为0.2 cm和0.3 cm。监测仪中探测γ射线部分的结构及材料参数见表 1，监测仪整体建模图如图 1(c)所示。

表 1

表 1 γ射线探测部分的结构及材料参数 Table 1 Structure and material parameters of the part which detects gamma ray 结构 Structure 材料 Material 组分（原子数比） Constituent (atom ratios) 密度 Density / g·cm-3 外壳 Shell 铝 Aluminum Al 2.7 屏蔽层 Shield 铅 Lead Pb 11.34 缓冲层 Buffer 聚乙烯海绵 Polyethylene sponge C:H=1:2 2.8×10-2 反射层 Reflector 氧化镁 Magnesium oxide Mg:O=1:1 3.58 探测器 Detector 闪烁晶体 Scintillation crystal Na:I=1:1 3.67 底座 Pedestal 光学玻璃 Optical glass Si:O=1:2 2.2 取样气体 Sample gas 空气 Atmosphere C=0.015 1%; N=78.443 7%; O=21.075%; Ar=0.467 1% 1.2×10-3

表 1 γ射线探测部分的结构及材料参数 Table 1 Structure and material parameters of the part which detects gamma ray

图 1(c)中，1为碘化钠晶体；2为氧化镁反射层；3为聚乙烯海绵；4为铝层；5为光学玻璃；6为探测孔；7为补偿铅孔预留区；8为铅层；9为取样气体；10为有机玻璃；11为铝层；12为空气。

利用MCNP按铅孔的大小和铅孔的厚度进行能量响应的模拟计算，通过对比不同铅孔和铅厚度的能量响应结果，从而寻找能量响应的最佳补偿方案。模型分类：铅孔半径分为0.5 cm、1.0 cm、1.5 cm、2.0 cm、2.5 cm、3.0 cm、3.5 cm，铅孔厚度分为0.2cm、0.3cm、0.4 cm、0.5 cm、0.6 cm、0.7 cm、0.8 cm、1.0 cm。为了与ICRP74号报告中的能量点相对应，模拟射线能量范围为0.02-3 MeV，共18个能量点。

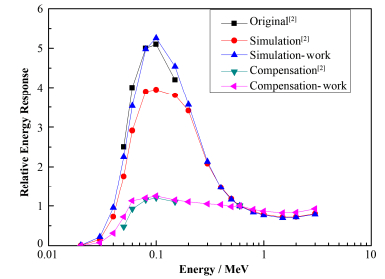
为了验证本工作建模计算的正确性，特对文献[2]的实验及模拟工作进行了对比计算，如图 2所示，由于文中的模拟能量点与文献中能量点不是一一对应，所以采用插值法。文献[2]中NaI晶体的尺寸为ø3.0 cm×2.0 cm，补偿铅孔的尺寸为：孔半径0.67cm，厚度为0.4 cm。

图 2

图 2 能量响应对比 Figure 2 Comparison of energy response

由图 2可以看出，本工作利用蒙特卡罗模拟计算值与文献结果基本一致，从而证明了本工作模拟计算的正确性。

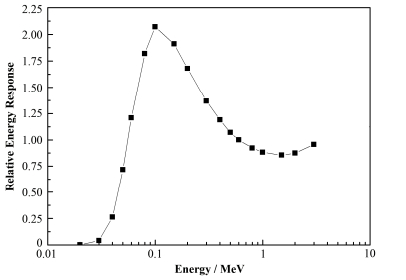
利用MCNP模拟计算放射性惰性气体监测仪中NaI晶体的能量响应，图 3为不加铅孔补偿时，所得到不同能量γ射线的能量响应与¹³⁷Cs的特征γ能量0.662 MeV处的能量响应比较曲线。

图 3

图 3 监测仪不加铅孔补偿时的能量响应 Figure 3 Energy response of the monitor without compensation

由图 3可知，γ射线能量在0.1 MeV时，能量响应为¹³⁷Cs特征γ射线的两倍以上。由于对不同能量的γ射线能量响应不同，探测器对低能部分响应过高，而对高能部分响应过低，那么在复杂辐射场中，如果低能辐射所占比例较大，测量的辐射场数值将会相应偏高；如果高能辐射所占比例较大，测量的辐射场数值将会相应偏低。由图 3可以看出，不加补偿时的能量响应高于JJG 393-2003^[9]中规定能量响应变化极限不超过±30%的要求，需要对监测仪中的γ探测器进行能量响应补偿。

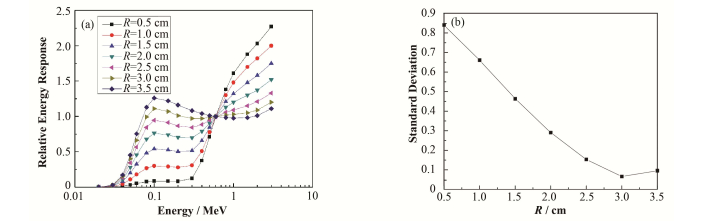
图 4(a)为铅孔厚度1.0 cm、不同铅孔半径下的相对能量响应，图 4(b)为不同铅孔半径下的能量响应标准偏差。

图 4

图 4 不同铅孔半径下的能量响应(a)及能量响应标准偏差(b) Figure 4 Relative energy response (a) and standard deviation of energy response (b) under different lead hole radius

图 4(a)中不同曲线代表铅孔厚度不变，铅孔半径R不同时的相对能量响应。从图 4(a)中可以看出，铅孔厚度不变时，随着铅孔半径的增加，低能段能响增加，而高能段的能响减小。

由于移动式放射性惰性气体监测仪监测γ射线的能量窗为0.08-2.5 MeV，所以仅考虑此能量范围内的能量响应。由图 4(b)可以看出，对0.08-3.0 MeV的γ射线，当R=3.0 cm时，能量响应补偿最佳。

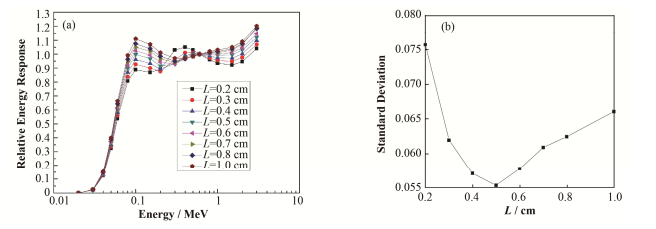
模拟计算铅孔半径为3.0 cm时，能量响应与铅孔厚度L的对应关系，如图 5(a)所示。对0.08-3.0MeV的γ射线，不同铅孔厚度下的能量响应标准偏差如图 5(b)所示。

图 5

图 5 不同铅孔厚度下的相对能量响应(a)及能量响应的标准偏差(b) Figure 5 Relative energy response (a) and standard deviation of energy response (b) under different lead hole thickness

由图 5可知，当铅孔半径为3.0 cm、厚度为0.5cm时，能量响应得到较好的补偿。

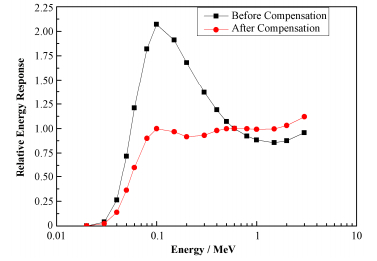
不加铅孔补偿前后的相对能量响应对比如图 6所示。由图 6可知，监测仪采用适当尺寸的铅孔进行补偿后，能量响应得到了较大的改善。

图 6

图 6 补偿前后的能响对比 Figure 6 Comparison of energy response before and after compensation

移动式放射性惰性气体监测仪利用NaI探测器测量γ射线，由于其测量不同能量γ辐射空气比释动能率时的能响差异，需要采取有效的补偿措施和优化监测仪结构。采用铅孔屏蔽补偿，首先利用MCNP软件模拟文献中ø3.0 cm×2.0 cm NaI探测器的能量响应，并与文献的结果进行对比，得到基本一致的结果，证明了模拟的正确性，然后利用MCNP模拟计算在不同半径、不同厚度铅孔屏蔽下的相对能量响应，并计算不同模型下的标准偏差，进而分析给出合适的铅孔屏蔽尺寸。监测仪中监测γ射线的能量范围为0.08-2.5 MeV，补偿后γ射线能量在0.08-3 MeV，相对能量响应在-10.1% -+11.2%，所得数据满足JJG 393-2003中规定能量响应变化极限不超过±30%的要求。模拟结果为监测仪补偿铅孔的加工提供了有力的理论依据，对监测仪性能的优化具有实际的指导意义。