辐照系统运行时，电子辐照加速器产生的电子和辐照物质发生轫致辐射产生的X射线经过屏蔽层的衰减后仍会对工作人员造成影响，需要合理的屏蔽计算以确保工作人员的安全。通常采用经验公式进行估算，但该方法有局限性，对实际应用中结构复杂的系统需要进行大量的简化，不能得到准确的结果，而蒙特卡罗(Monte Carlo, MC)方法可以基于复杂几何系统模拟粒子输运，是解决复杂系统中粒子输运问题最常用的方法。MCNP5 (Monte Carlo N Particle Transport Code)作为大型的MC程序包，具有强大的几何能力、丰富的减方差技术以及截面数据，适用于模拟复杂几何结构系统中光子的输运，本文基于MCNP5平台进行模拟计算。

本文所研究的辐照系统屏蔽层很厚，粒子需穿过130cm厚度混凝土地板或40cm厚钢板到达计数区，属于典型的深穿透问题。前人对解决电子辐照加速器的屏蔽计算和深穿透问题做了大量研究^[1-8]。但对于屏蔽计算问题着重于评估剂量分布，缺少在解决该问题中减方差技术的分析；而对于深穿透问题，构建的几何结构简单，侧重于理论分析而缺少在实际应用中的指导。本文从辐射防护的目的出发，真实地构建电子辐照加速器系统的几何模型，计算粒子穿过130cm混凝土地板或40cm厚钢板后加速器主厅中的点剂量，分析各个减方差技术单独使用和不同组合使用在该实际应用问题中的计算效果，以找出快速、有效的减方差方案解决深穿透问题，服务于实践；同时，本文减方差技术的选取也适用于其它MC程序包。

选择合适的减方差技术在解决深穿透问题中是很重要的，下面简单介绍本文中使用的减方差技术。

几何重要性抽样函数(IMP)：通过IMP卡给每个栅元设置一个重要性，控制粒子在栅元间的输运，粒子进入感兴趣栅元，通过使粒子分裂而使更多的粒子进入计数区；粒子进入不感兴趣栅元，通过轮盘赌减少粒子抽样。

源偏倚：包括能量、角度、时间偏倚等，它通过偏倚源变量以抽样较多感兴趣区域的粒子。该偏倚为抽样提供一个概率分布，这个概率分布不是源的真实分布，抽样粒子的权重将被修改为真实分布概率除以偏倚概率分布的值，保证结果无偏和总权重守恒。

指数衰减：通过将伪截面替代原物理过程中的真实截面，以达到粒子输运过程中指向相应方向的目的，同时调整粒子的权重。

分步输运法：统计粒子在物质中输运一段距离后各变量的分布情况，包括能量分布函数、方向分布函数、位置分布函数等，然后从分布函数中抽样粒子进行下一步的输运，从而增加了抽样的源粒子数，降低抽样统计涨落。

DXTRAN球：其原理是用两个同心球将感兴趣区域包含。球外粒子每次碰撞都产生一个DXTRAN粒子，该粒子以确定概率散射到DXTRAN球表面，期间不发生碰撞，权重按确定性输运计算。该方法将尽量多粒子引到感兴趣区域附近，增加粒子对感兴趣区域产生贡献的可能。

权重窗：其原理是在空间或能量下设立一系列权重区间，而达到减方差的目的。粒子权重高于权重窗上限时进行分裂，低于权重窗下限时进行轮盘赌，从而每个粒子的权重都在权窗以内，去除权重异常的粒子从而减少其所带来的误差。

点探测器计数：在MC中也称为下次事件估算(A Next-event Estimator)，使用指向概率法计算粒子对探测器的贡献，其物理意义：由源或碰撞点发出的粒子对探测器的贡献，等于其权重乘以其向探测器发射的概率，再乘以粒子经过R距离到达探测器而不发生进一步碰撞的概率，其中R是源点或碰撞点到探测器的距离。

典型的电子辐照加速器系统的屏蔽室一般由两层构成，上层为加速器主厅，下层为辐照室。本文中电子辐照加速器区别于典型直筒式高频高压加速器，是一种半自屏蔽式的新型辐照加速器，其采用卧式角尺形设计，将高频高压源与加速部分分为两体，成直角连接，并在加速管外设计保护环和屏蔽钢筒进行自屏蔽；同时，加速器屏蔽钢筒底座和基座直接相接，电子束经过加速管中的高压电场获得加速，从高压系统中引出后，经由漂移管穿过基座进入辐照室，漂移管和基座之间无间隙，而典型的直筒式高频高压加速器的电子束经由漂移管穿过通孔进入辐照室，通孔和漂移管之间有较大空间，会导致X射线通过间隙进入加速器主厅。漂移管连接位于扫描磁铁内的芯管，扫描磁铁产生相互垂直的交变磁场，使电子束均匀地引出并照射被照物质。具体的MC几何建模如图 1所示。

图 1

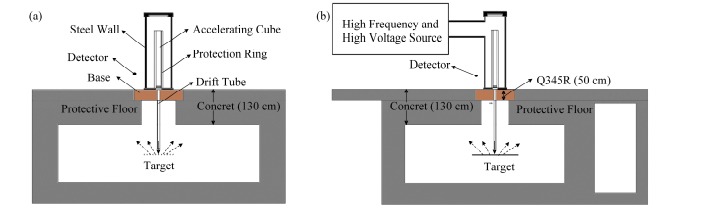
图 1 电子辐照加速器系统的蒙特卡罗模型 (a) xz方向，(b) yz方向 Figure 1 The MCNP calculation model of electron irradiation accelerator (a) xz cross-section views, (b) yz cross-section views

本文中电子辐照加速器的能量为2MeV、束流50mA，将辐照物质等效为长度200cm、半径1cm的铜丝（铜靶）。选择探测点位置距离加速管钢筒壁30cm，距离地面100cm，选取该点的原因是工作人员需要到达该点对机器进行检测和维护，此外，该点的剂量组成相对复杂，既有穿过钢板的光子，又有穿过混凝土地板或同时穿过两者的光子，同时，加速管外屏蔽钢筒的散射光子也对该点产生剂量贡献，所以选取该点进行减方差技术的探讨。

本文首先分析不使用任何减方差技术及使用单个减方差技术模拟粒子输运的计算误差和效率；之后，在分步输运的基础上，组合一种其它减方差技术模拟粒子的输运，得到计算效率高的减方差技术和分步输运组合，再结合其它减方差技术模拟计算，依次类推，直到组合所有本文中的减方差技术；最后，分析权窗减方差技术的计算效率。分步输运时，使用分步输运减方差技术模拟电子打靶后粒子的分布时，分两步模拟：第一步，模拟电子打靶产生的光子，利用MCNP5计数卡中的能量卡(En)和余弦卡(Cn)，将穿过球面源的粒子用面计数卡(F1)按照能量箱和角度记录下来，得到分别按照能量和角度制成的能谱和方向谱，作为下一步计算的新的光子源，本文中新光子源位置设置为原靶中心，球面半径1m，将0-2MeV按0.02MeV的间隔、出射光子方向和入射光子方向夹角0°-180°按5°的间隔进行划分；第二步，利用第一步计算的结果，从打靶后的光子源开始，再对源抽样进行后续计算。此外，本文重点研究减方差技术，对计算结果的剂量率值不做分析。

将F5点探测器半径设置为0.5 cm，通过转换因子卡(DE/DF)实现单个粒子注量转换为剂量，单位为每粒子pGy，再乘以剂量转换因子化为以Gy·h⁻¹为单位的吸收剂量率。其中，剂量转换因子选自NIST (National Institute of Standards and Technology)物理测量实验室(Physical Measurement Laboratory)中X射线质量吸收系数数据库(X-ray Mass Attenuation Coefficients)^[9]，光子和电子的截止能量分别是0.01MeV、0.05MeV。本文中MCNP5（版本1.51）运行平台为Windows 8工作站，28核56个线程，CPU主频2.2GHz，实际计算时用50个线程并行计算，所有模拟计算中追踪的粒子数为2.0x10⁹。

在计算时发现，束流形状和靶的几何结构对光子能谱影响很大，本文模拟了两种情况，第一种情况根据实际模型，将电子窗等效为120cm×8cm矩形平面源，靶为11根铜丝，半径为1cm，每两根铜丝之间间隔10cm，和实际辐照情况相符；第二种情况束流等效为直径为1cm的圆形单向平面源，将靶等效为圆柱形铜靶，厚度大于电子在靶中的一倍射程（本文取2cm），直径比束流直径大一个量级（本文取20cm）^[10]。由图 2可知，在两种情况下，光子能谱峰值都出现在0.06MeV，处于0.02-1.0MeV的光子依次为97%、94.13%，能量谱差异不大；飞行方向两者差异较大，铜丝靶光子的飞行方向在0°-90°之间占比29.6%，光子飞行方向在90°时最少，圆柱形铜靶光子的飞行方向集中在100°-180°，占比99.6%.

图 2

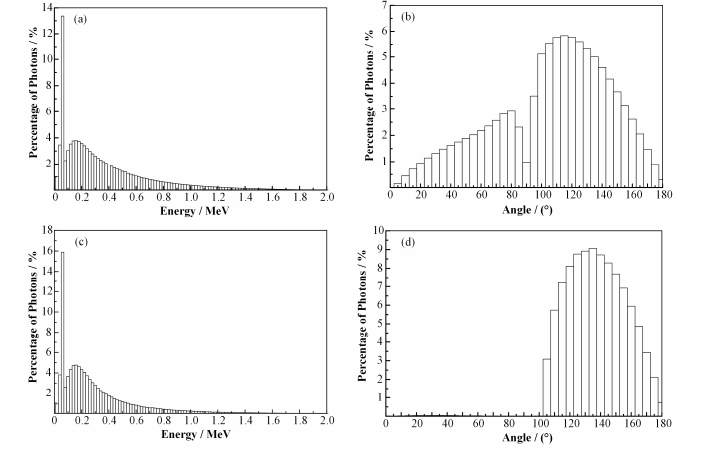
图 2 新光子源的能谱分布和方向谱分布 (a、b)电子打铜丝靶，(c、d)电子打圆柱形铜靶 Figure 2 Energy and angular distribution of new photon source (a, b) Copper wire target, (c, d) Copper cylinder target

将模拟结果和其他研究进行对比，如钦佩等^[11]对辐照加工低能电子束轫致辐射的能谱分析中，当其模拟条件和文中的第二种情况类似时，无论是能量谱还是方向谱，分布趋势一致，说明本文模拟电子打靶的方法正确。同时和雷洁瑛等^[10]的研究中关于电子打靶进行对比，发现能量谱的趋势相似，但是光子的方向谱差异较大，主要是靶的厚度相差较大造成。因此，建议靶的几何结构贴近实际模型，避免在新的输入源中引入误差，造成剂量计算的“硬误差”。

由图 3可看出，单个减方差技术计算平均值差异大、相对误差大，结果不可信。但相比于无减方差技术时，三种减方差技术均降低了相对误差，其中分步输运的相对误差最小；进一步分析，从表 1可知，分步输运的计算效率最高，计算时间相比于无减方差技术缩短了6.6倍，因为分步输运将电子打靶得到的光子谱作为新的源输入，避免大量的抽样粒子模拟电子打靶，提高计数效率和结果的可信度，减少计算时间。几何分裂通过提高防护地板和基座的重要性以增加抽样粒子，降低计数误差。DXTRAN球包含探测点，产生的DXTRAN粒子以指定的概率对计数做贡献，提高探测器的抽样，减小计数误差，本文中设置DXTRAN小球的半径为0.5cm。由图 3和表 1可知，分步输运在该深穿透问题中有最明显的减方差效果。

图 3

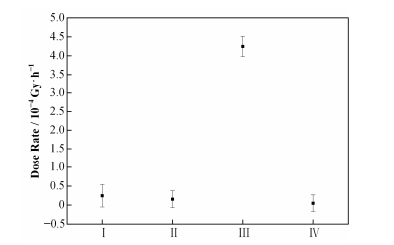
图 3 单个减方差技术计算平均值 Figure 3 Mean value of single variance reduction technique

表 1

表 1 单个减方差技术计算效果比较 Table 1 Computational efficiency of single variance reduction technique 序号 No. 减方差技术 Variance reduction techniques 相对误差 Relative error FOM 计算时间 Calculating time/min Ⅰ 无减方差技术 No variance reduction techniques 0.3596 0.001 796 Ⅱ 几何分裂 Geometry splitting 0.2685 0.005 372 Ⅲ 分步输运 Step-step transform 0.1191 0.021 121 Ⅳ DXTRAN 0.1864 0.005 194

表 1 单个减方差技术计算效果比较 Table 1 Computational efficiency of single variance reduction technique

由图 4可知，分步输运结合其他一种减方差技术时，源偏倚相对误差(0.0274)最小，几何分裂、指数衰减和DXTRAN球的相对误差均大于0.05；以分步输运和源偏倚为基础，再组合其它减方差技巧，计算平均值稳定且相对误差小，当4种减方差技术组合使用时，得到最小的相对误差。在表 2中，从计算时间分析，减方差技术不同，计算时间差异较大，其中几何分裂计算时间最长；不同减方差技术组合使用时，计算时间随组合减方差类型的增长呈上升趋势，当4种技术组合使用时，计算时间最长；从品质因数(Figure of Merit, FOM)分析，两种、3种和4种减方差技术组合均大于单个减方差技术（源偏倚除外）。这是因为减方差技术通常会增加抽样粒子单个历史的模拟时间，使计算时间增加，而FOM和R²与T的乘积成反比，其中R是计算值和平均值的偏差，T是计算时间，而减方差技术使R²的减少大于增加的时间T，从而在计算时间增加的情况下有更好的FOM值，一般抽样较好的问题，FOM应该趋于稳定。

图 4

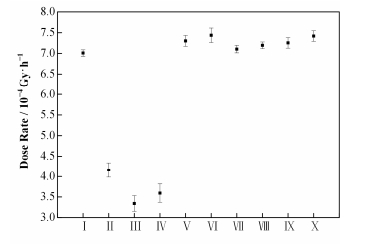
图 4 分步输运组合其它减方差技术计算平均值 Figure 4 Mean value of step-step transform used in conjunction with other variance reduction techniques

表 2

表 2 分步输运和组合其它减方差技术计算效果比较 Table 2 Computational efficiency of step-step transform used in conjunction with other variance reduction techniques 序号 No. 减方差技术 Variance reduction techniques 相对误差 Relative error FOM 计算时间 Calculating time/min Ⅰ 源偏倚 Biasing the source 0.0274 1.300 116 Ⅱ 几何分裂 Geometry splitting 0.0607 0.036 312 Ⅲ 指数衰减 Exponential transform 0.1075 0.078 113 Ⅳ DXTRAN球 DXTRAN 0.1107 0.057 161 Ⅴ 源偏倚、DXTRAN球 Biasing the source and DXTRAN 0.0242 0.350 149 Ⅵ 源偏倚、几何分裂 Biasing the source and geometry splitting 0.0216 0.360 277 Ⅶ 源偏倚、指数衰减 Biasing the source and exponential transform 0.0284 1.000 123 Ⅷ 源偏倚、指数衰减、DXTRAN球 Biasing the source, exponential transform and DXTRAN 0.0220 0.640 166 Ⅸ 源偏倚、指数衰减、几何分裂 Biasing the source, exponential transform and geometry splitting 0.0404 0.760 294 Ⅹ 源偏倚、几何分裂、指数衰减、DXTRAN球 Biasing the source, geometry splitting, exponential transform and DXTRAN 0.0163 0.280 387

表 2 分步输运和组合其它减方差技术计算效果比较 Table 2 Computational efficiency of step-step transform used in conjunction with other variance reduction techniques

在图 4和表 2中，单独使用源偏倚时，计算值相对误差小，计算效率高，但其输出结果中FOM值没有趋于稳定，说明抽样不够好。这是因为源偏倚的选择具有相当的主观性，和使用者对减方差技术的理解及经验有很大关系。本文中源偏倚中的角度偏倚，抽样粒子以94.4%的概率集中在以源到探测点方向为轴、圆锥角为20°的圆锥范围内，后改变偏倚角度，将圆锥角设置为10°，计算平均值、相对误差和FOM均有较大的变化，进一步说明表 2中结果的不稳定性，需要和其它减方差技术组合使用，但源偏倚仍有最明显的降低方差效果。本文中指数衰减的方向从靶中心指向探测点（VECT卡），并定义每个栅元的指数衰减方向（EXT卡）。

综合§2.2和§2.3中的常规减方差技术，分步输运和源偏倚的减方差效果最好。常规减方差技术对使用者的要求比较高，需要使用者深刻理解减方差技术，为了降低减方差技术的使用难度，下面的计算会使用自动减方差技术-权窗减方差。

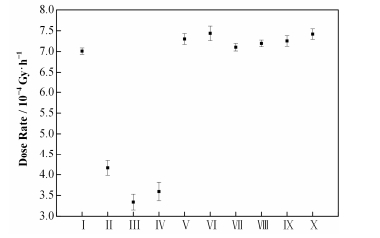
使用权窗减方差，在分步输运和源偏倚的基础上，使用WWG (Weight Window)卡追踪1.0×10⁸粒子生成权窗。接下来将权窗结果作为输入，在分步输运和源偏倚的基础上组合其他减方差技术，各减方差组合计算结果如图 5、计算效率如表 3所示。

图 5

图 5 权窗、分步输运和源偏倚组合其他减方差技术计算平均值 Figure 5 Mean value of weight window, step-step transform and biasing the source used in conjunction with other variance reduction techniques

表 3

表 3 权窗、分步输运和源偏倚组合其它减方差技术计算效果比较 Table 3 Computational efficiency of weight window, step-step transform and biasing the source used in conjunction with other variance reduction techniques 序号 No. 减方差技术 Variance reduction techniques 相对误差 Relative error FOM 计算时间 Calculating time/min Ⅰ 几何分裂 Geometry splitting 0.0412 0.500 72 Ⅱ 指数衰减 Exponential transform 0.0372 0.490 73 Ⅲ DXTRAN球 DXTRAN 0.0359 0.360 79 Ⅳ 指数衰减、DXTRAN球 Exponential transform and DXTRAN 0.0343 0.410 91 Ⅴ 几何分裂、DXTRAN球 Geometry splitting and DXTRAN 0.0307 0.560 88 Ⅵ 几何分裂、指数衰减、DXTRAN球 Geometry splitting, exponential transform and DXTRAN 0.0162 0.640 92

表 3 权窗、分步输运和源偏倚组合其它减方差技术计算效果比较 Table 3 Computational efficiency of weight window, step-step transform and biasing the source used in conjunction with other variance reduction techniques

由图 5和表 3可知，权窗减方差技术和其他减方差技术结合后，计算结果平均值相对稳定，相对误差均小于0.05，可信度高；同时，计算时间大大的降低。以上结果表明，权窗是一种非常好的减方差技术。

综合§2.2、§2.3和§2.4的结果，分步输运和源偏倚在本研究中明显优于其他常规减方差技术；权窗和常规减方差技术均能得到可信的计算结果，但权窗相比于常规减方差技术在计算效率上有明显的优势，大大地缩短了计算时间；同时权窗的产生是MCNP中WWG卡自动产生的，相比于几何分裂，具有更好的客观性，降低因使用者对减方差技术的理解不够带来的干扰因素。以上说明，使用权窗和常规减方差技术均能解决复杂模型中的深穿透问题，但权窗具有更高的计算效率、更好的客观性和可操作性。

本文列出多种减方差技巧并做了简要介绍说明，对比多种减方差技术在复杂模型深穿透问题中的减方差效果。从计算结果可看出，分步输运和源偏倚相比于其他常规减方差技术可以更好地降低计算误差，它们和几何分裂、DXTRAN球和指数衰减组合使用时，可以进一步地降低计算误差，有效提高结果的可信度；权窗相对于常规减方差技术具有更好的计算效率、客观性和易用性，以权窗、分步输运和源偏倚为基础，再组合其它减方差技术，可以很好地解决实际应用中复杂模型的深穿透问题。

关于本文，有两点需注意：第一，本文研究的是单个位置的减方差技术，如果同时计算多个位置的剂量分布，要特别注意减方差技术的使用，比如DXTRAN小球，避免小球之间有重叠部分，源偏倚时角度偏倚选取的正确性以及计数卡的选取等；第二，减方差技术具有人为因素，需要使用者较好地理解MCNP中的减方差技术，这在Booth^[12]的研究中也明确指出。

目前，减方差技术的使用很大程度上依赖于使用者的经验，希望以后可以基于MC程序包开发出自动获取减方差技术，提高计算效率，方便用户使用。