2. 中国科学院大学 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
上海光源(Shanghai Synchrotron Radiation Facility, SSRF)是一台高性能的中能第三代同步辐射光源。同步辐射装置对磁场的长期稳定度以及精度有很高的要求,为其供电的电源必须提供高稳定的励磁电流。
通常加速器电源一般采用深度负反馈维持电流的稳定性,但由于电压陷落[1],会导致电源的直流母线电压波动,磁铁电源本身由于受带宽限制,无法快速抑制此波动,从而在电源的输出侧产生突变电流。
为改善上述问题,采用并联补偿结构,利用小电流电源的快速响应特性,以及极强的自适应性等特点,设计突变电流补偿器。该突变电流补偿器直接对负载的波动电流进行补偿,这种补偿方式对补偿响应速度有极高的要求。
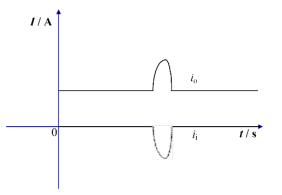
1 补偿器基本原理及结构 1.1 基本原理电流补偿器的工作原理是通过检测电源输出的突变波形,产生一个与其极性相反的波形,由基尔霍夫电流定律(Kirchhoff’s Current Law, KCL)中并联电路电流相加的原理,使得突变电流在负载端被抑制。突变电流与补偿电流关系如图 1所示,突变部分与补偿电流相加为零,达到了抑制突变电流的效果。
|
图 1 突变电流与补偿电流关系 Figure 1 The relationship between the abrupt current and the compensating current |
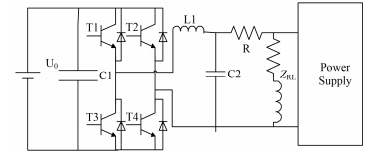
为不改变原加速器电源的结构,尽量不改变电源的负载特性,所以选择补偿器与主电源并联于负载上的方式[2],如图 2所示,其主体结构与开关电源结构相同,由一个稳定直流电压源对补偿器供电,通过脉宽调制(Pulse-Width Modulation, PWM)技术控制H桥的4个绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor, IGBT)的开关,T1与T4由同一个PWM波控制,T2与T3由另一组极性相反(不考虑死区时间)的PWM波控制,再经过LC(电感、电容)低通滤波降低开关频率对补偿器的输出电流影响,在LC与负载间加一电阻R,从而较稳定地控制输出电流的大小与极性对负载ZRL进行补偿。
|
图 2 并联补偿器结构图 Figure 2 Structure diagram of shunt compensator |
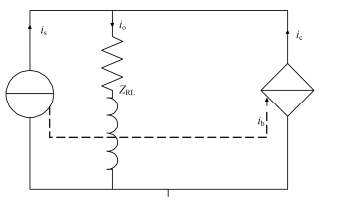
由于补偿器输出端的滤波电容也并联于负载上,对于负载而言,增加了一个极点,对于负载特性有影响。为降低其影响,在输出端增加一个电阻R,使得其极点远离虚轴,并适当将滤波电容减小,让极点靠近实轴,减小其输出振荡。使得该补偿器可等效于一个可控电流源[3],等效模型如图 3所示。
|
图 3 补偿器等效电路 Figure 3 Equivalent circuit of compensator |
补偿器(图 3)受控电流源,其输出电流ic由指令电流ib决定,指令电流ib由加速器电源的输出is决定。
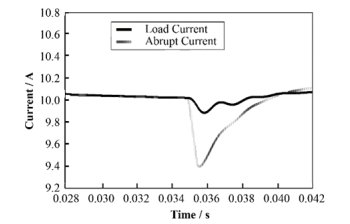
1.3 原理验证与仿真为了验证上述方案的可行性,以及其补偿效果利用MATLAB/Simulink,按照上述工作原理,对补偿过程进行搭建,建立了一个完整的补偿模型。该仿真先搭建了一个电源,其直流母线在0.03 s时有明显衰减,并且只通过开关电源本身的负反馈做不到很好的突变抑制。产生突变电流通过并联补偿器对感性负载进行补偿后,对突变的电流有明显抑制。仿真结果如图 4所示。
|
图 4 补偿过程仿真结果 Figure 4 Simulation waveform of compensatory process |
突变电流衰减峰值为0.602 A,经补偿后得到的负载电流衰减峰值为0.115 A,突变的抑制比为80.89%,衰减峰值与补偿电流的峰值的补偿延迟为0.0002 s。可以说明补偿器对突变电流的补偿有明显的效果,上述理论是可行的。
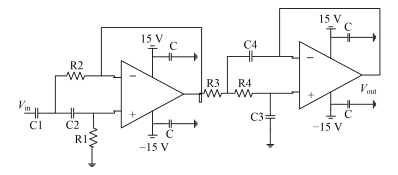
1.4 控制原理检测突跳,先从电源输出端用直流电流传感器(Direct Current-Current Transformer, DCCT)采集输出电流,经过模拟带通滤波器[4]。
|
图 5 模拟带通滤波器 Figure 5 Analog bandpass filter |
该带通滤波器的传输函数为:
| $\begin{array}{l} H(s) = \frac{{{s^2}{C_1}{C_2}{R_1}{R_2}}}{{{s^2}{C_1}{C_2}{R_1}{R_2} + s{R_2}\left( {{C_1} + {C_2}} \right) + 1}} \times \\ \;\;\;\;\;\;\;\;\;\;\;\frac{1}{{{s^2}{C_3}{C_4}{R_3}{R_4} + s{C_3}\left( {{R_3} + {R_4}} \right) + 1}} \end{array}$ | (1) |
3 dB带宽为:
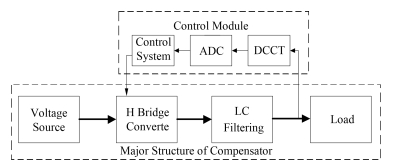
得到突变电流信号经过模数转换器(Analog-to-Digital Converter, ADC)转换成数字信号,通过数字化控制卡对H桥控制,形成一个闭环受控系统[5],控制框图如图 6所示。
|
图 6 补偿器整体框图 Figure 6 Block diagram of compensator |
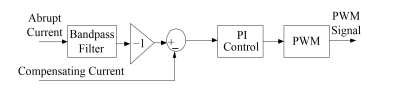
数字信号进入控制卡后,令其反相,同时通过DCCT对补偿器的输出电流采样,同样通过ADC之后,将信号送入控制卡中,将提取的反相突变信号作为参考信号,补偿器输出信号则为被控信号,得到二者的差值,进行比例积分(Proportional Integral, PI)控制运算[6],再经过PWM得到4个两组PWM控制信号分别控制4个IGBT,PWM信号的占空比由PI控制运算的结果决定,通过占空比决定输出电压的大小,控制框图如图 7所示。
|
图 7 控制框图 Figure 7 Block diagram of controller |
整体系统采用闭环控制系统,为了保证控制系统对突变信号的快速响应,必须保证整个控制系统的传递函数的相频响应,最大限度降低控制系统对控制信号中突变信号成分的相位延迟,指令电流为ir,补偿器输出电流为ic,系统闭环控制函数[7]为:
| $\left[{{i_{\rm{r}}}\left( s \right)-{i_{\rm{c}}}\left( s \right)} \right] \times \left( {{k_{\rm{p}}} + \frac{{{k_i}}}{s}} \right) \times P\left( s \right) = {i_{\rm{c}}}\left( s \right)$ | (2) |
| ${i_{\rm{c}}}\left( s \right) = \frac{{\left( {{k_{\rm{p}}} + \frac{{{k_i}}}{s}} \right) \times P\left( s \right)}}{{1 + \left( {{k_{\rm{p}}} + \frac{{{k_i}}}{s}} \right) \times P\left( s \right)}}{i_{\rm{r}}}\left( s \right)$ | (3) |
P(s)为主电路传递函数,由式(2)、(3)得到指令电流与输出电流的相位差为:
| $\varphi (\theta ) = \angle \left| {\left( {{k_{\rm{p}}} + \frac{{{k_i}}}{s}} \right) \times P\left( s \right)} \right| - \angle \left| {1 + \left( {{k_{\rm{p}}} + \frac{{{k_i}}}{s}} \right) \times P\left( s \right)} \right|$ | (4) |
从式(4)可以看出,对相位主要的延迟影响决定于比例积分系数kp、ki以及负载特性,主电路的负载特性为固有参数,为保证响应的速度,又不使系统欠阻尼,对于kp、ki的选择极其重要。若比例积分的模无穷大,或者相位差为零,则式(4)都为零,为保证PI控制的稳定性,其模必须为有限值,所以减小比例积分的相位差是减小指令电流与输出电流相位差的关键。
2 实验验证仿真验证了其可行性后,为进一步验证上述原理的可行性,搭建了补偿器的实验平台,将补偿器与快校正电源并联,初步测试了补偿的效果。
电网陷落是电压突然降到10%-90%,并持续0.05个周波到1 min,其持续时间一般大于0.001 s,补偿器响应速度和补偿器输出带宽有关,补偿器的带宽能够达到1 kHz,基本能满足对电压陷落引起的电流突变的补偿。所以该实验,先让快校正电源模拟产生一个150 Hz左右(<1 kHz)的突变电流,通过DCCT得到输出电流,让其经过一个带通滤波器得到突变信号,将其负信号经过补偿器的ADC卡[8]传给其控制卡,通过控制卡控制补偿器的H桥对负载进行补偿,负载为一块1.5 mH的磁铁,其负载特性为RL。该ADC卡利用高精度的模数转换器AD7960,其采样频率可以高达100 kHz,其有效分辨率位数为18位,该采样系统精度保证了实验的准确性。
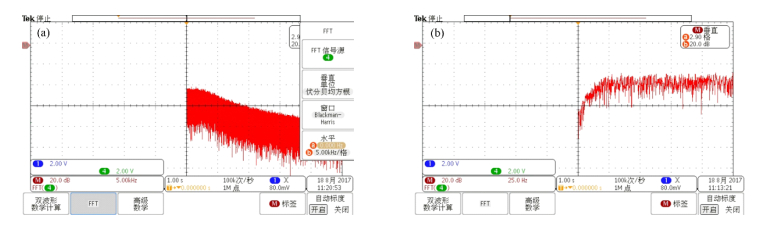
该实验使用了模拟带通滤波器,设计上该滤波器的3 dB带宽为[25 Hz, 4.2 kHz],并用函数信号发生器产生高斯白噪声,对其滤波特性进行测试,测试结果如图 8所示。
|
图 8 带通滤波器幅度频率响应 (a)低通部分,(b)高通部分 Figure 8 Amplitude-frequency response of bandpass filter (a) Lowpass field, (b) High pass field |
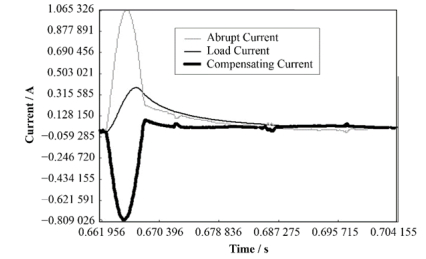
该实验对校正电源输出的突变电流、与补偿器输出的补偿电流以及最终负载电流进行了检测与比较,得到的实验结果如图 9所示。由图 9可以看出,有明显的补偿效果,突变电流由约1 A的峰值电流经补偿后负载的峰值电流降到了0.35 A,验证了上述原理与仿真结果相符。
|
图 9 突变电流补偿 Figure 9 Compensation of abrupt current |
通过上述的仿真以及实际实验平台上的测试,验证了并联突变电流补偿器对突变电流的抑制效果,在补偿器的补偿范围内能自适应对电源输出进行补偿,并在不改变原电源的结构下保证加速器电源运行的稳定性,有很强的实用性和研究的价值。不过从结果也能看出,还有能继续提升的地方,如:加快补偿器的响应速度,增加补偿器的补偿能力即提高补偿器输出的功率谱,加强其适应性以及泛用性,使之能够在各种电源上使用,都是后续改进的方向。
| [1] |
蔡永生, 李国杰. DVC动态电压补偿器[J]. 实验与技术管理, 2007, 24(6): 59-61. CAI Yongsheng, LI Guojie. Hardware experiment on dynamic voltage compensator (DVC)[J]. Experimental Technology and Management, 2007, 24(6): 59-61. |
| [2] |
Wu Z Q, Zhang G R. Research on sliding mode control based on exact feedback linearization for single-phase shunt APF[C]. 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, 2016: 1350-1356. http://ieeexplore.ieee.org/document/7512486/
|
| [3] |
肖国春, 裴云庆, 姜桂宾, 等. 大功率低纹波稳定电源用直流有源滤波器[J]. 电力电子技术, 2001, 35(4): 1-4. XIAO Guochun, PEI Yunqing, JIANG Guibin, et al. DC active filter for large power and low ripple stable supply[J]. Power Electronics, 2001, 35(4): 1-4. |
| [4] |
Bruce Carter. 运算放大器权威指南[M]. 第4版. 孙宗晓, 译. 北京: 人民邮电出版社, 2010: 57-81. Bruce Carter. Op amps for everyone[M]. 4th Ed. SUN Zongxiao, Tran. Beijing: Posts & Telecom Press, 2010: 57-81. |
| [5] |
Fahmy A M, Abdelsalam A K, Kotb A B. Unified fuzzy-logic based controller for dual function 4-leg shunt APF with predictive current control[C]. 2015 17th European Conference on Power Electronics and Applications (EPE'15 ECCE-Europe), Geneva, 2015: 1-10. http://ieeexplore.ieee.org/document/7309185/
|
| [6] |
Dang P, Petzoldt J. A new control method for eliminating the 2nd harmonic at the DC link of a shunt APF under an unbalanced and nonlinear load[C]. Proceedings of the 2011 14th European Conference on Power Electronics and Applications, Birmingham, 2011: 1-5. http://ieeexplore.ieee.org/document/6020236/
|
| [7] |
王伟利, 刘小宁, 王磊. 强磁场装置有源直流滤波器设计[J]. 电力自动化设备, 2007, 27(3): 96-98. WANG Weili, LIU Xiaoning, WANG Lei. Design of active DC filter for high magnetic field device[J]. Electric Power Automation Equipment, 2007, 27(3): 96-98. |
| [8] |
朱晓慧, 谭松清, 李瑞. 高精度同步数据获取系统的研制[J]. 核技术, 2014, 37(11): 110101. ZHU Xiaohui, TAN Songqing, LI Rui. Research and design of high precision synchronization data acquisition system[J]. Nuclear Techniques, 2014, 37(11): 110101. DOI:10.11889/j.0253-3219.2014.hjs.37.110101 |


