2. 中国科学院大学 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
近年来,束团相空间重建技术作为测量束团相空间分布的方法,在许多加速器上得到了应用。例如:英国的ALICE (Accelerator and Lasers In Combined Experiments)装置[1]通过改变四极铁的强度来改变旋转角度,利用FBP (Filtered Back Projection)算法[2-4]进行相空间重建,德国DESY (Deutsches Elektronen Synchrotron)的PITZ (Photo Injector Test Facility at Zeuthem)装置[5-6]有一段专用相空间重建段,该段由三个FODO结构和4个观测靶组成,根据观测靶上得到的电子束斑图像,利用MENT (Maximum Entropy)[7-9]算法进行相空间重建。FLASH[10]、UMER (University of Maryland Electron Ring)[2]、TRIUMF[11]、PSI (Paul Scherrer Institute)和SNS (Spallation Neutron Source)[12]等装置也分别利用不同的重建算法进行相空间重建。向导利用ART (Algebraic Reconstruction Technique)算法在清华大学光阴极电子枪上重建电子枪出口处的相空间分布[13]。
上海软X射线自由电子激光装置(Shanghai Soft X-ray Free Electron Laser facility, SXFEL)作为中国的第一台X射线自由电子激光装置,对电子束流品质提出了很高的要求。该装置直线段出口处的束流能量设计目标为840 MeV,能散要求在0.1%-0.15%之间,峰值流强约为500 A,电荷量为0.5 nC,归一化发射度约为2 mm·mrad[14]。该装置初步建设已经基本完成,现已进入调试阶段。为精确测量电子束团的相空间分布,本文分别利用FBP算法和MENT算法在SXFEL装置专用束测段(BI1)进行相空间重建。实验方法及结果为高亮度电子束精确调控提供直接测量工具。
1 相空间重建原理简介束团相空间重建基于计算机断层扫描技术。当电子束团经过四极铁、漂移段或其他传输元件时,电子束团在传输元件的作用下会受到旋转、拉伸和剪切的作用。束团图像可以在观测靶上得到。改变观测靶前面四极铁的强度,可以得到不同的束斑图像,电子束团横向相空间分布可以通过这些束斑图像用重建算法得到。
通常情况下,束团相空间的分布为长且窄的椭圆,如果相空间变得非常窄,用这种非常窄的相空间得到的投影通常不能准确反映相空间的真实分布,重建误差可能比较大,因此,重建结果比较依赖投影角度的选择。在归一化相空间中,束团的β=1,α=0,对应于相关性
| $\left( {\begin{array}{*{20}{c}} x\\ {x'} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\sqrt \beta }&0\\ { - \frac{\alpha }{{\sqrt \beta }}}&{\frac{1}{{\sqrt \beta }}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_N}}\\ {{{x'}_N}} \end{array}} \right)$ | (1) |
如果想要重建A处归一化相空间,那么束流相当于从重建点处归一化相空间传输到重建点处真实相空间,然后经过四极铁和漂移段传输到观测点B上。重建点A处归一化相空间与观测点B之间的旋转角度
| $ \left\{ \begin{matrix} \tan \theta =\tan \mu \text{=}\frac{{{{R}_{12}}}/{\sqrt{{{\beta }_{A}}}}\;}{{{{R}_{11}}\sqrt{{{\beta }_{A}}}-{{R}_{12}}{{\alpha }_{\operatorname{A}}}}/{\sqrt{{{\beta }_{\operatorname{A}}}}}\;} \\ \rho =\sqrt{\beta {}_{B}} \\ \end{matrix} \right. $ | (2) |
式中:Rij代表从重建点到观测点的传输矩阵元;μ代表重建点和观测点之间的相移;下标A和B分别代表重建点A和观测点B处的Twiss参数。
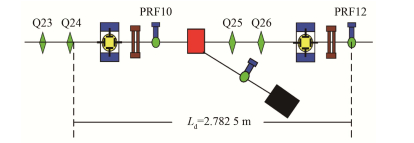
2 相空间重建 2.1 图像数据处理SXFEL装置有一段专门用于束流测量的BI1段,BI1段的部分结构示意图如图 1所示,束团相空间重建点选择在Q24铁入口处。Q25、Q26四极铁电源处于关闭状态,从Q24出口处到PRF12观测靶中间的空间相当于漂移段。Q24铁的有效长度为20 cm。
|
图 1 SXFEL装置BI1段部分结构示意图 Figure 1 Part of the structure diagram of BI1 section in SXFEL facility |
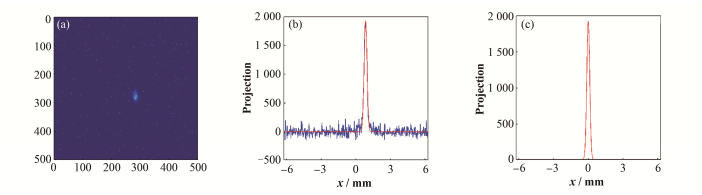
进行实验时,束团能量为160 MeV,电荷量约为400 pC。改变Q24铁的电流值,在PRF12靶上获取不同四极铁强度对应的束斑图像,利用束斑在x方向上的投影进行相空间重建。SXFEL装置使用的观测靶主要为YAG (Yttrium Aluminum Garnet)屏和OTR (Optical Transition Radiation)屏,OTR屏与YAG屏相比,具有更高的空间分辨率(可达微米),但灵敏度比YAG屏低约3个量级。所以,OTR一般用于束流截面较小、而流强较高的情况。SXFEL装置产生的束团亮度较高,由于YAG屏的灵敏度较高,在YAG屏上观测到的束斑已经严重饱和。显然,使用OTR屏要比YAG屏效果好。实验中,为了尽量减小误差,我们取同一电流值下的三组图像数据,对三组数据求平均得到该电流值下的图像数据。电子束团图像数据由500×500的矩阵组成,典型图像如图 2(a)所示。水平方向上,每个像素点代表 25mm。选择没有电子束斑的地方作为本底噪声进行扣除,具体选择方法为:200×500的上半部分矩阵投影与150×500的下半部分矩阵投影之和乘以该部分图像所占整个图像比例的倒数。扣除本底噪声后将图像在水平方向上进行投影,采用高斯拟合对投影进行平滑处理(图 2(b))。为了减小束流轨道偏移带来的误差,将拟合后投影最大值所在的位置作为x方向的中心点,最后得到投影曲线(图 2(c))。
|
图 2 束斑图像(a)、投影曲线及高斯拟合曲线(b)、拟合后的投影曲线(c) Figure 2 Beam profile(a), projected curve of the image and Gaussian fitting curve (b), and Gaussian fitting curve (c) |
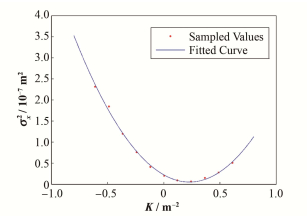
若要重建束团的归一化相空间,根据前面的理论,必须知道重建点和观测点处的β值。首先,我们可以利用四极铁扫描法得到重建点处束团发射度和Twiss参数。根据四极铁扫描法的原理[16],选择11个不同电流值对应的束斑图像进行测量,得到的拟合曲线如图 3所示,经计算得到Q24入口处的归一化发射度εnx=1.7910mm·mrad,Twiss参数αx=1.0227,βx=7.7962。
|
图 3 四极铁扫描法拟合曲线 Figure 3 Fitted curve of quadrupole scan method |
束流从Q24铁入口处到PRF12的x方向的传输矩阵为R=RDRQ,其中:RD为漂移段的传输矩阵;RQ为四极铁的传输矩阵。当四极铁电流值大于0时:
| ${R_Q}{\rm{ = }}\left( {\begin{array}{*{20}{c}} {\cos (\sqrt k {L_Q})}&{\sin (\sqrt k {L_Q})/\sqrt k }\\ { - \sqrt k \sin (\sqrt k {L_Q})}&{\cos (\sqrt k {L_Q})} \end{array}} \right)$ | (3) |
式中:LQ为四极铁有效长度;k=299.792g/E为四极铁聚焦参数,g为四极铁磁场变化梯度,由四极铁的固有属性和电流值决定;E为束团能量。当四极铁电流值小于0时:
| ${R_Q} = \left( {\begin{array}{*{20}{c}} {\cosh (\sqrt {\left| k \right|} {L_Q})}&{\sinh (\sqrt {\left| k \right|} {L_Q})/\sqrt {\left| k \right|} }\\ {\sqrt {\left| k \right|} \sinh (\sqrt {\left| k \right|} {L_Q})}&{\cosh (\sqrt {\left| k \right|} {L_Q})} \end{array}} \right)$ | (4) |
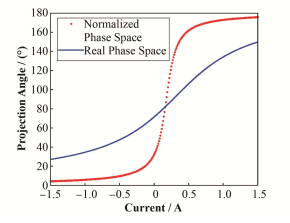
Q24铁的电流值可以达到的变化范围为-5 -5A之间,但当电流值比较大的时候,电子束团发散非常严重,实际可用的图像的电流值变化范围约在-1.5 -1.5A。根据计算得到的Twiss参数,可以得到在真实相空间和归一化相空间中不同电流值所对应的旋转角度。旋转角度曲线如图 4所示。
|
图 4 归一化相空间与真实相空间旋转角度 Figure 4 Rotation angles of normalized phase space and real phase space |
由计算可知,在真实相空间中,旋转角度范围比较有限,为27°-150°,存在较大的角度空挡,不足以进行相空间重建。而在归一化相空间中,旋转角度范围为4°-176°,旋转角度范围是在归一化相空间中重建的又一突出优点。
2.3 MENT算法重建MENT算法是一种迭代类重建算法,可以利用较少的投影(通常为3-5个)进行重建。我们用4个投影进行相空间重建。为了重建束团的归一化相空间,必须知道归一化相空间在4个角度上的投影值。观测点处的投影值可以利用靶上得到的束斑图像在x轴上投影得到。重建点处的β值已由四极铁扫描法算出,观测点处的β值可根据重建点处的β值由传输矩阵推算得到。知道了观测点和重建点处的β值便可得到归一化相空间中的投影值。得到归一化相空间分布后,根据归一化相空间与真实相空间的关系(式(1))便可得到束团的真实相空间分布。
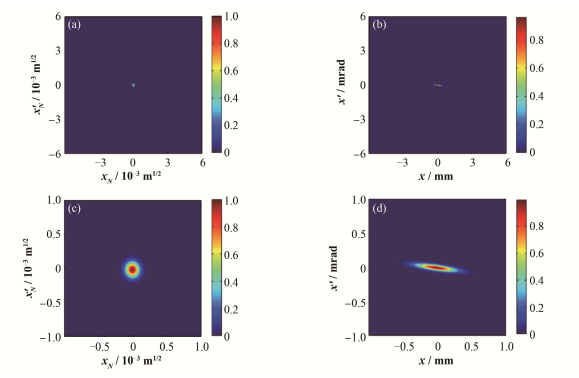
在归一化相空间中选择45°等间隔的投影角度进行重建,分别为20°、65°、110°、155°。归一化相空间和真实相空间重建结果如图 5所示。图 5(a)、5(b)为12.5 mm×12.5 mm(观测靶上的图像实际尺寸)范围内的重建结果,为了使重建后的相空间更加清晰,利用同一组数据在2 mm×2 mm范围内重建,图 5(c)、5(d)为重建结果。
|
图 5 12.5 mm×12.5 mm (a、b)和2 mm×2 mm (c、d)范围内相空间重建结果 (a, c)归一化相空间,(b, d)真实相空间 Figure 5 Reconstructed phase space within the range of 12.5 mm×12.5 mm (a, b) and 2 mm×2 mm (c, d) (a, c) Normalized phase space, (b, d) Real phase space |
用MENT算法重建时规定,当通过迭代得到的投影与实验测得束斑投影的相对误差在1%以内时停止迭代。在2 mm×2 mm范围内重建时的迭代次数与相对误差演变如表 1所示。
| 表 1 迭代次数与相对误差 Table 1 Number of iterations and relative errors evolution |
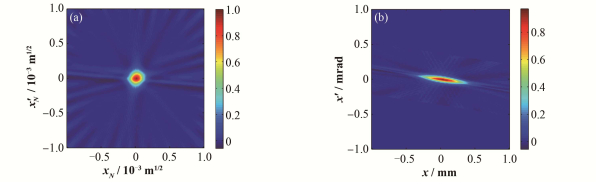
FBP算法属于解析类重建算法,需要利用较多的投影进行重建。由于在归一化相空间中的旋转角度为4°-176°,存在8°的角度空挡,因此,我们从5°-175°每隔10°选择一个角度,共选用18个角度在归一化相空间中进行重建。在2mm×2mm范围内的重建图像如图 6所示。图 6中比较清晰的射线是伪影(在真正的相空间中是不存在的)。由此可以看出,18个角度的投影对于FBP算法来说依然较少。在少量投影的情况下,FBP算法只能重建出相空间的大致轮廓,而不能重建出相空间的精细结构。图 6(b)的相空间分布轮廓与图 5(d)的相空间分布轮廓相同,验证了MENT算法重建结果的正确性与优越性。
|
图 6 FBP算法重建结果 (a)归一化相空间,(b)真实相空间 Figure 6 Reconstructed results with FBP algorithm (a) Normalized phase space, (b) Real phase space |
电子束团的发射度和Twiss参数由式(5)-(8)计算:
| $\left\langle {{x^2}} \right\rangle = \beta \varepsilon $ | (5) |
| $\left\langle {{{x'}^2}} \right\rangle = \gamma \varepsilon $ | (6) |
| $\left\langle {xx'} \right\rangle = - \alpha \varepsilon $ | (7) |
| $\varepsilon = \sqrt {\left\langle {{x^2}} \right\rangle \left\langle {{{x'}^2}} \right\rangle - {{\left\langle {xx'} \right\rangle }^2}} $ | (8) |
式中:<>代表求平均值;ε为几何发射度,归一化发射度
| 表 2 各测量结果对比 Table 2 Comparison of the measurement results |
通过对各测量结果的对比可以看出,四极铁扫描法和MENT算法计算得到的束团归一化发射度和Twiss参数非常接近,说明MENT算法重建出的相空间比较准确。而由FBP算法重建出的相空间,由于受到伪影的影响,计算结果不准确,不能用来衡量束团的发射度和Twiss参数。在少量投影的情况下,FBP算法只能重建出相空间分布的大致轮廓。
3 误差分析对测量结果进行误差分析,其误差来源主要分为理论误差和实验误差两个方面。
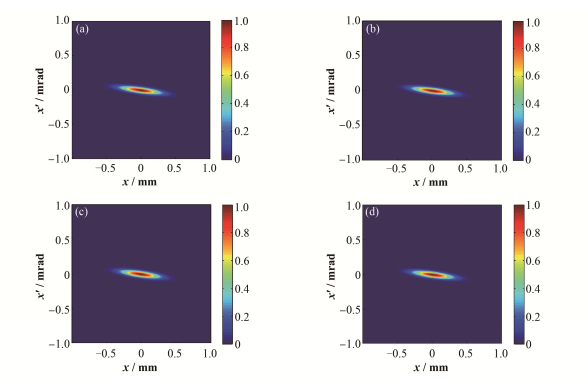
3.1 理论误差在重建束团的归一化相空间时,要用到束团在重建点和观测点处的β值。本文利用四极铁扫描法计算β值。四极铁扫描法需要假设束团相空间分布为椭圆并且采用薄透镜近似。因此,由四极铁扫描法计算得到的β值本身就存在一定的误差。为了了解四极铁扫描法所测β值的误差对重建结果的影响,我们对所测的β值分别给予±5%和±10%的误差再进行重建。重建结果如图 7所示,用重建图像数据计算得到的发射度如表 3所示。
|
图 7 不同β误差重建结果 (a) 5%,(b)-5%,(c) 10%,(d)-10% Figure 7 Reconstruction results corresponding to different β errors (a) 5%, (b)-5%, (c) 10%, (d)-10% |
| 表 3 不同β误差对应的发射度 Table 3 Emittances corresponding to different β errors |
通过以上对比可以看出,相空间分布的变化通过肉眼几乎看不出区别,重建结果对β误差不是特别敏感。
另外,在计算传输矩阵时,我们作了束团x方向和y方向没有耦合的假设。利用MENT算法计算的过程中,多次用到插值法,并且在将束团从归一化相空间转换到真实相空间的过程中也用到了插值法,这不可避免地引起了误差。在用MENT算法重建相空间时,我们只采用了4个角度的投影,更多的投影会使重建结果更加准确。
3.2 实验误差与理论误差相比,实验上的误差对重建结果的影响会更大一些。在SXFEL装置中,电子束团的尺寸较小,亮度较高,要求观测屏具有较高的分辨率。实验中我们采用OTR屏来获取束斑图像。虽然OTR屏具有较高的空间分辨率,但是我们从图 2(a)可以看到,束斑只占整个屏幕的很小的一部分,这对获取更详细的束斑信息造成一定的影响。另外,束斑抖动也会对获取正确的束斑信息造成一定的影响。我们取同一电流值下的三组图像数据,对三组数据求平均得到该电流值下的图像。当束斑存在抖动时,会导致取平均后的束斑尺寸变大、亮度降低,这将会导致所测的发射度偏大。
4 结语本文根据相空间重建理论,利用MENT算法和FBP算法对SXFEL装置BI1段的电子束团相空间进行重建。采用四极铁扫描法得出电子束团在重建点处的β值,并推算到观测点,从而在归一化相空间重建分布。比较了不同重建算法的实验结果,并对实验结果的误差来源进行了分析。结果表明:MENT算法能够很好地重建出电子束团相空间分布。相空间重建技术能够给SXFEL装置束流测量及调试提供相应的技术手段。
| [1] |
Ibison M G, Hock K M, Holder D J, et al. ALICE tomography section:measurements and analysis[J]. Journal of Instrumentation, 2012, 7(4): 221-224. DOI:10.1088/1748-0221/7/04/P04016 |
| [2] |
Stratakis D, Kishek R A, Li H, et al. Tomography as a diagnostic tool for phase space mapping of intense partical beams[J]. Physical Review Special Topics-Accelerators and Beams, 2006, 9(11): 112801. DOI:10.1103/PhysRevSTAB.9.112801 |
| [3] |
Kak A C, Slaney M, Wang G. Principles of computerized tomographic imaging[J]. Medical Physics, 2002, 29(1): 107-107. DOI:10.1137/1.9780898719277 |
| [4] |
McKee C B, Oshea P G, Madey J M J. Phase space tomography of relativistic electron beams[J]. Nuclear Instruments & Methods in Physics Research Section A-Accelerators Spectrometers Detectors and Associated Equipment, 1995, 358(1): 264-267. DOI:10.1016/0168-9002(94)01411-6 |
| [5] |
Rimjaem S, Asova G, Bähr J, et al. Measurements of transverse projected emittance for different bunch charges at PITZ[C]. Proceedings of FEL2010, Malmö, Sweden, 2010: 410-413. https://www.researchgate.net/publication/50385961_Measurements_of_Transverse_Projected_Emittance_for_Different_Bunch_Charges_at_PITZ
|
| [6] |
Asova G, Grabosch H J, Gross M, et al. First results with tomographic reconstruction of the transverse phase space at PITZ[C]. Proceedings of FEL2011, Shanghai, China, 2011: 543-546. https://www.researchgate.net/publication/268052396_First_results_with_tomographic_reconstruction_of_the_transverse_phase_space_at_PITZ
|
| [7] |
Minerbo G. MENT:a maximum entropy algorithm for reconstruction a source from projection data[J]. Computer Graphics and Image Processing, 1979, 10(1): 48-68. DOI:10.1016/0146-664X(79)90034-0 |
| [8] |
Mottershead C T. Maximum entropy beam diagnostic tomography[J]. IEEE Transaction on Nuclear Science, 1985, 32(5): 1970-1972. DOI:10.1109/TNS.1985.4333784 |
| [9] |
Hock K M, Ibison M G. A study of the maximum entropy technique for phase space tomography[J]. Journal of Instrumentation, 2013, 8(2): P02003. DOI:10.1088/1748-0221/8/02/P02003 |
| [10] |
Honkavaara K. Electron beam characterization at PITZ and the VUV-FEL at DESY[C]. Proceeding of the 27th International Free Electron Laser Conference, California, America, 2005: 411-417. https://www.researchgate.net/publication/228732641_Electron_Beam_Characterization_at_PITZ_and_the_VUV-FEL_at_DESY
|
| [11] |
Rao Y N, Baartman R. Transverse phase space tomography in TRIUMF injection beamline[C]. Proceedings of IPAC2011, San Sebastian, Spain, 2011: 1144-1146. https://www.researchgate.net/publication/233421588_Transverse_Phase_Space_Tomography_in_TRIUMF_Injection_Beamline
|
| [12] |
Reggiani D, Seidel M, Allen C K. Transverse phase-space beam tomography at PSI and SNS proton accelerators[C]. Proceedings of IPAC2010, Kyoto, Japan, 2010: 1128-1130. https://www.researchgate.net/publication/228812620_Transverse_phase-space_beam_tomography_at_PSI_and_SNS_proton_accelerators
|
| [13] |
向导. 高亮度电子束发射度、束长和束斑的先进测量方法研究[D]. 北京: 清华大学, 2008. XIANG Dao. Advanced beam measurements of emittance, bunch length and beam size for high-brightness electron beam[D]. Beijing: Tsinghua University, 2008. |
| [14] |
Huang D Z, Gu Q, Zhang M, et al. Design study of the Linac of the Shanghai soft X-ray free electron laser facility[C]. Proceedings of FEL 2012, Nara, Japan, 2012: 141-143. http://www.irgrid.ac.cn/handle/1471x/859898
|
| [15] |
Hock K M, Ibison M G, Holder D J, et al. Beam tomography research at Daresbury laboratory[J]. Nuclear Instruments & Methods in Physics Research Section A-Accelerators Spectrometers Detectors and Associated Equipment, 2014, 753(14): 38-55. DOI:10.1016/j.nima.2014.03.050 |
| [16] |
许珊珊, 叶恺容, 陈永忠. SSRF直线加速器束流发射度测量[J]. 核技术, 2008, 31(3): 174-177. XU Shanshan, YE Kairong, CHEN Yongzhong. Emittance measurement for electron beam of SSRF linac[J]. Nuclear Techniques, 2008, 31(3): 174-177. |


