核反应堆在运行过程中，堆芯的温度不断变化，对于某些高温核能系统，因温度效应造成的反应性偏差会对反应堆安全造成较大影响^[1−2]。为了准确模拟反应堆内中子与材料的相互作用，必须在模拟时以在线(on-the-fly)的方式获取不同温度对应的反应截面。目前，国内外核截面在线生成方法中，以MCNP6的曲线拟合法使用较为普遍^[3]。该方法以共振能区的Adler-Adler公式为依据，推导出某一能量下各共振反应截面与展宽温度之间的关系，使用Kernel Broadening多普勒展宽方法生成一定温度范围、一定温度间隔的展宽截面，再根据这些展宽截面使用回归分析方法计算得到与温度相关的曲线拟合参数^[4]。由于Kernel Broadening方法生成目标温度截面效率偏低，致使该方法生成不同温度拟合参数的性能不高^[5]。

本文在MCNP6的曲线拟合法基础上，提出使用数值积分法代替Kernel Broadening方法，按能量范围不同分别使用双指数方法与Gauss-Hermite方法，以提高展宽截面生成效率。

在自由气体模型假设下，一般认为靶核热运动速度满足麦克斯韦-玻尔兹曼分布。假设当前温度反应截面为${\sigma _{{T_1}}}(E)$，其中：E为入射中子能量；T为靶核材料的热力学温度。将当前T₁温度截面展宽为T₂温度(T₁ > T₂)的截面的展宽方程可表示为：

式中：β=A/[k(T₂−T₁)]，A=M/m；m为中子质量；M为靶核质量；k为玻尔兹曼常数；E_r为中子与靶核的相对能量^[6]。

引入无量纲变量x、y，使得x=(βE_r)^1/2、y=(βE)^1/2，根据式(1)中被积对象的取值范围可将该式改写成如下分段形式：

该分段形式的依据是指数函数的衰减特性^[7]。使用解析方法求解式(2)的方法称为Kernel Broadening方法，由于该方法使用泰勒级数展开及误差函数求解，使得该方法计算效率较低。由于MCNP6的参数拟合中采用该方法作为不同温度截面的生成方法，故有必要对该方法加以改进。

对于积分$I = \int_a^b {f\left( x \right){\text{d}}x} $，如采用梯形数值积分法则，被积函数f (x)在积分区间(a, b)范围内的数值积分表达式为：

式中：N为积分级数；h为等量步长。通过变量替换，可将积分I变换为：

代入式(4)后，得：

这里ψ(x)称为双指数函数，它是一个将区间$\left( { - \infty , \infty } \right)$映射到$\left( {a, b} \right)$的绝对连续单调递增函数^[8−9]。ψ(x)其中一种表示形式为：

为简化计算，可将双指数函数简写成节点与权重的形式，即：

相应地，式(5)可改写成：

因此，当y≤4时将式(5)以双指数函数变换表示后，可得：

其中：$ f\left( x \right) = {x^2}{\sigma _{{T_1}}}\left( x \right)[{{\text{e}}^{ - {{\left( {x - y} \right)}^2}}} - {{\text{e}}^{ - {{\left( {x + y} \right)}^2}}}]$ 。

为验证方法的有效性，表 1给出了反应堆常用核素(¹H、¹⁰B、¹⁶O、⁹⁰Zr、²³²Th、²³⁵U、²³⁸U)在y≤4，步长h=1/16，k∈[−4, 4]条件下，分别使用双指数方法与Kernel Broadening方法生成不同温度(600 K、900 K与1200 K)总截面时的最大相对偏差。

表 1

表 1 不同方法在线生成不同温度总截面的最大相对偏差 Table 1 Max relative deviation of the total cross section of the various target temperatures generated with different methods 典型核素 Typical nuclides 最大相对偏差 Max relative deviation / % 600 K 900 K 1200 K 1H 0.00259 0.00128 0.00172 10B 0.00577 0.00467 0.00356 16O 0.00171 0.00173 0.00241 90Zr 0.00242 0.00151 0.00127 232Th 0.00124 0.00376 0.00212 235U 0.00350 0.00548 0.00381 238U 0.00252 0.00259 0.00241

表 1 不同方法在线生成不同温度总截面的最大相对偏差 Table 1 Max relative deviation of the total cross section of the various target temperatures generated with different methods

从表 1可以看出，在步长h=1/16时使用双指数方法在线生成的核截面与Kernel Broadening方法相对偏差均小于0.006%，证明了该方法的准确性。

当y > 4时，令x=z+y，代入式(2)可得：

对于式(10)中指定的积分项$f\left( z \right){{\text{e}}^{\text{-}{{z}^{\text{2}}}}}$，可使用Gauss-Hermite积分公式近似表示为：

其中：$f(z) = {(z + y)^2}\sigma (z + y)$，${{z}_{k}}$为Hermite多项式${{H}_{n}}$的节点，定义为：

将式(2)进一步推导得：

考虑到Kernel Broadening方法中x的取值范围(y−4≤x < y+4)，当y > 4时式(13)积分项中的 $ \int_{-\infty }^{-y}{~}{{(z+y)}^{2}}{{\sigma }_{{{T}_{1}}}}\left( z+y \right){{\text{e}}^{-{{z}^{2}}}}\text{d}z$ 贡献很小，可忽略不计。此时目标温度的截面${\sigma _{{T_2}}}\left( y \right)$可表示为：

根据上述分析，表 2给出了反应堆常用核素(¹H、¹⁰B、¹⁶O、⁹⁰Zr、²³²Th、²³⁵U、²³⁸U)在y > 4、节点k=16条件下，使用Gauss-Hermite方法与Kernel Broadening方法生成不同温度(600 K、900 K、1200K)总截面时的最大相对偏差。

表 2

表 2 不同方法生成目标温度总截面的最大相对偏差 Table 2 Max relative deviation of the total cross section of the target temperature generated with different methods 典型核素 Typical nuclides 最大相对偏差 Max relative deviation / % 600 K 900 K 1200 K 1H 0.00108 0.00029 0.00059 10B 0.03804 0.03825 0.03541 16O 0.03956 0.05587 0.06790 90Zr 0.08398 0.09205 0.09857 232Th 0.04038 0.05001 0.08901 235U 0.03635 0.04156 0.08487 238U 0.04789 0.05563 0.08834

表 2 不同方法生成目标温度总截面的最大相对偏差 Table 2 Max relative deviation of the total cross section of the target temperature generated with different methods

从表 2可以得出，在节点k=16时，使用Gauss- Hermite方法生成的核截面与Kernel Broadening方法相对偏差均小于0.1%，证明了该方法的准确性。

MCNP6的拟合参数法首先基于某一温度截面，通过Kernel Broadening方法生成某一能量E_i在T₀, T₁, …, T_n温度点的等效截面${\sigma _0}, {\sigma _1}, \cdots , {\sigma _n}$，通过这些温度点与等效截面建立如下关系：

式中：k取值与截面随温度变化关系有关，通常值取为8；系数${a_i}, {b_i}, c$与能量及反应截面类型呈线性关系，其结果可采用矩阵奇异值分解(Singular Value Decomposition, SVD)求解。经一系列推导后，可得任意温度总截面(${\sigma _t}$)、辐射俘获截面(${\sigma _\gamma }$)与裂变截面(${\sigma _f}$)的拟合形式：

其具体计算流程如图 1所示。

图 1

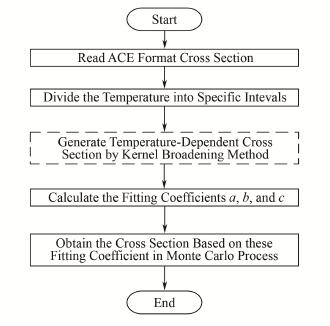
图 1 原曲线拟合法截面在线生成流程 Figure 1 On-the-fly generation procedure of cross section using original curve fitting method

该方法主要的时间消耗为指定温度间隔的Kernel Broadening截面展宽(图 1虚框显示)。为此，本文基于MCNP6拟合参数程序fit_otf，编写了基于数值积分法的拟合参数程序ni_fit_otf，在截面展宽中使用本文提出的数值积分法代替Kernel Broadening方法(图 1虚框显示)，提高截面的生成效率，其生成流程见图 2。

图 2

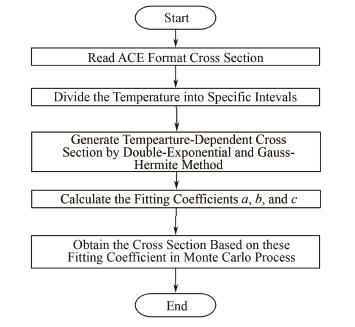
图 2 基于本文方法的曲线拟合法截面在线生成流程 Figure 2 Curve fitting method of cross section on-the-fly generation process based on integration method

图 3给出了使用ni_fit_otf与fit_otf生成300 K温度间隔下典型核素总截面的生成效率之比。从图 3可以看出，前者中的数值积分方法的计算效率比后者中的Kernel Broadening方法平均高10倍以上，轻核部分加速近40倍，证明了该方法核截面生成效率相对于原始方法获得了较大的提升。

图 3

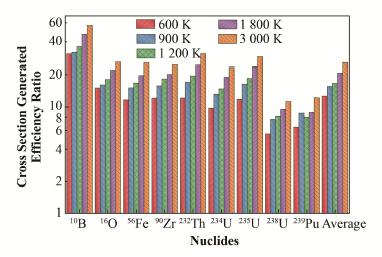
图 3 不同方法生成典型核素截面的生成效率比 Figure 3 Generation efficiency ratio of typical cross sections generated by using different methods

本文采用多普勒反应性系数基准例题测试数值积分方法的有效性，该基准例题采用一个栅元结构模型，中心燃料为UO₂，燃料外的包壳材料为Zr，最外层为含¹⁰B及轻水的正方体反射层，反应性多普勒系数基准例题轴向设置为无穷大，使用全反射边界条件^[10]。模型结构如图 4所示。

图 4

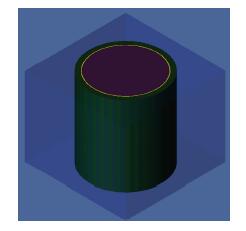
图 4 反应性多普勒系数基准例题模型 Figure 4 Model of Doppler coefficient of reactivity

该例题中慢化剂的温度固定为600 K，其中燃料区的温度有600 K和900 K两种，分别代表热态零功率(Hot Zero Power)与热态满功率(Hot Full Power)。该基准模型中通过分别计算燃料温度为600 K和900 K时的有效增殖因数，得到温度引起的反应性多普勒系数 $\text{ }\!\!~\!\!\text{ }{{D}_{\text{c}}}$ ，其表达形式如下：

其中：Δρ_Dop=(k_HFP−k_HZP)/(k_HFP×k_HZP)，ΔT_fuel=300 K，分别计算0.711%、1.6%、2.4%、3.1%、3.9%、4.5%、5.0%富集度下的燃料多普勒系数。反应性多普勒系数基准模型旨在验证反应性多普勒系数计算结果的准确性，要求计算结果与基准值的相对偏差不超过10%^[10]。

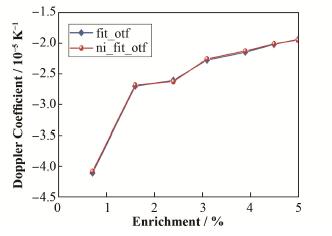
本文使用原始温度为293.6 K的ACE格式截面^[11]，分别使用ni_fit_otf与fit_otf曲线拟合法生成拟合参数，通过MCNP6计算反应性多普勒系数。每代计算粒子数为100000，总计模拟5100代并舍去前100个非活跃代。UO₂燃料的反应性多普勒系数的计算结果如图 5所示。

图 5

图 5 反应性多普勒系数结果对比 Figure 5 Results comparison of reactive Doppler coefficient

结果显示：使用ni_fit_otf方法计算得到的不同富集度下反应性多普勒系数均与fit_otf方法计算结果相当，最大相对偏差仅为1.54%，表明本文方法计算结果的精度符合基准例题要求，验证了本文方法的准确性与有效性。

本文针对MCNP6的曲线拟合在线截面生成方法中截面展宽效率较低问题，提出使用数值积分法代替Kernel Broadening方法，按能量范围不同分别使用双指数方法与Gauss-Hermite方法生成不同温度截面，提高截面的生成效率。典型核素测试结果显示，数值积分方法的曲线拟合计算效率比采用Kernel Broadening方法平均高10倍以上，多普勒反应性系数基准例题结果显示，数值积分方法的曲线拟合与原始方法精度相对偏差在1.54%内，验证了本文方法的有效性，可用于反应堆多物理耦合计算。