最佳估算与不确定性分析方法已经成为核电站性能与安全的重要评价依据，已受到国内外学者、工业界和安全评审当局的重视。其中，核反应堆物理计算的不确定性分析是核电厂最佳估算与不确定性分析的重要内容之一。影响核反应堆物理计算结果的不确定性因素有很多，比如核截面、反应堆物理计算模型和计算方法等，而由积分实验测量的不精确的中子截面已经成为了影响核反应堆物理计算重要的不确定度来源之一^[1]。为了研究中子截面造成的计算结果的不确定度，国际上已经研发了较多的核数据不确定性分析程序，主要有：TSUNAMI (1D, 2D, 3D)、XSUSA、CASMO-4、SUS3D、UNICORN、SAINT等。SCALE中TSUNAMI与XSUSA分析核数据为238截面库，协方差数据是SCALE中44GROUPCOV产生协方差矩阵ZZ-SCALE6.0/COVA-44G；而CASMO-4分析的E60200的70群截面库，采用的协方差数据与TSUNAMI相同；UNICORN与SAINT的分析对象分别是WIMS-172库、107群，两者的协方差数据是由NJOY在ENDF/B-Ⅶ.1或JENDL-4.0下直接产生^[2-4]。在进行不确定性分析时，以上程序大多使用了NJOY程序产生协方差数据，而实际的协方差数据信息均由程序使用的核评价数据库决定。

进行截面不确定性分析时，首先需得到分反应道的截面数值，比如辐射俘获截面、弹性散射截面和非弹性散射截面等。由于这些分反应道截面不常用于反应堆物理计算中，因此部分WIMS-D核数据库中并未直接存储这些反应道的具体截面数值。但不确定性分析中需要直接调用这些截面数值，因此，截面数值的计算方法对不确定性分析结果也会产生影响。本文依托于自主开发的基于抽样方法的不确定性分析程序SUACL，对这些截面的计算方法进行了深入研究。对于SUACL程序验证详见文献[5]。根据测试结果，提出在不确定性分析中扰动前的截面初值应与初始核评价库中的截面理论值尽可能保持一致的建议。通常截面的不确定度信息储存于其协方差数据中，因此，协方差数据是不确定性分析的必要条件。考虑到基于不同的核评价数据库产生的协方差矩阵存在显著的差异，而少有程序系统分析了其间差异给不确定性分析结果的影响，本文利用NJOY基于不同核评价数据库产生的协方差，在SUACL程序上开展与分析其对核反应堆物理计算响应的不确定性分析的影响。发现基于不同核评价数据库制作的协方差可使同一分析对象的不确定性分析结果发生量级以上的波动。以²³⁸U的裂变截面为例，由JEFF3.2产生的协方差数据库下得到的不确定度比基于ENDF/B-Ⅶ.1与JENDL4.0产生的协方差计算的结果小4个数量级。因此，挑选与分析堆型相关核评价数据库产生的协方差数据也是实施核数据不确定性分析的关键。

目前常用的核数据不确定性与敏感性分析(U/S)方法可分为两类：确定论分析方法和统计抽样法。与确定论方法相比，基于统计抽样方法的不确定性分析方法具有方法简单、程序易实现和考虑高阶效应影响的优势，且在反应堆不确定性分析中越来越受到重视^[6-7]。但基于抽样方法的不确定性分析方法难以进行灵敏性系数计算，特别是进行局部灵敏度计算。即使某些条件可以进行计算，比如对特定反应道每个能群的截面单独做微扰计算，但计算工作量巨大，计算效率较低。已有观点提出基于抽样方法的不确定性分析方法的灵敏性系数计算新方法，未来有望实现统计抽样法的敏感性分析的功能^[8]。统计抽样法可以用4个步骤来概括^[9]：确定分析问题中输入参数的概率分布；产生不确定性分析的输入样本；所有样本进行指定计算程序计算（输运计算、燃耗方程等），得到的响应值；对输出结果进行统计处理，进行不确定性分析与敏感性分析。

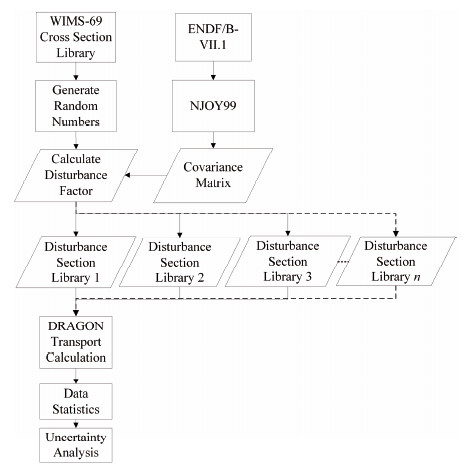
考虑到反应堆物理分析的系统具有多输入多响应、数值分析过程较为复杂、计算精度的需求与编程实现的难易等特点，SUACL程序采用统计抽样法来分析核数据的不确定度。核数据不确定性分析的实现流程详见图 1。首先利用NJOY产生的协方差矩阵和WIMSD格式的数据库产生微扰后的数据库样本，分析数据库的样本容量根据Wilks^[10]公式(1)决定。当置信度γ与覆盖范围α都等于0.95，则最小取样数N≥93，样本容量设定为100^[11]。然后利用这些数据库样本和组件计算程序DRAGON进行多相变量的不确定性分析。目前，SUACL程序已实现了多核素多反应道的截面微扰功能。最后利用式(2)进行标准偏差计算，然后利用式(3)计算相对不确定度。

图 1

图 1 SUACL不确定性分析的计算流程图 Figure 1 Calculation flow chart of uncertainty analysis in the SUACL

式中：σ_R为相应量R的标准偏差；$\bar R$为相应量的平均值；U_r为对应量的相对不确定度。

核数据不确定性分析过程中，扰动截面的一致性原则是指扰动的截面各个反应道之间是否满足自洽的要求，而本文讨论截面一致性是未扰动的截面初值与原始库中截面理论真值是否保持一致的问题，即截面初值的计算应符合截面库中截面存放的规律的问题。核数据不确定性分析的目的是为了确定由输入参数的不确定传递给输出响应的不确定度大小^[9]。因此，实施不确定性分析的首要步骤是获得实际分析的截面值。截面在截面库中是按照核素与反应道的类型存放的，常见的反应道(MT)如表 1所示^[12]。

表 1

表 1 常见的截面反应道与符号 Table 1 The common reaction types of cross section and its label 反应道 Reaction type 反应 Reaction 截面符号 Lable 1 (n, total) ${\sigma _{\rm{t}}}$ 2 (n, elas) ${\sigma _{{\rm{elas}}}}$ 4 (n, inelas) ${\sigma _{{\rm{inel}}}}$ 16 (n, 2n) ${\sigma _{2{\rm{n}}}}$ 17 (n, 3n) ${\sigma _{3{\rm{n}}}}$ 18 (n, fiss) ${\sigma _{\rm{f}}}$ 102 (n, capture) ${\sigma _{\rm{ \mathsf{ γ} }}}$ 452 ${v_{{\rm{total}}}}$ ${v_{{\rm{total}}}}$

表 1 常见的截面反应道与符号 Table 1 The common reaction types of cross section and its label

除了表 1中提到各种截面外，还有吸收截面(${\sigma _{{\rm{a}}}}$)、输运截面(${\sigma _{{\rm{tr}}}}$)、总散射截面(${\sigma _{\rm{s}}}$)等。在不确定性分析中将截面视为两大类：基础型截面与合成型截面。上述的截面按类分别为：${\sigma _{{\rm{elas}}}}$、${\sigma _{{\rm{inel}}}}$、${\sigma _{{\rm{2n}}}}$、${\sigma _{{\rm{3n}}}}$、${\sigma _{\mathop{\rm f}\nolimits} }$、${\sigma _{\rm{r}}}$均为基础型截面，${\sigma _{\rm{t}}}$、${\sigma _{\rm{a}}}$、${\sigma _{{\rm{tr}}}}$、${\sigma _{\rm{s}}}$属于合成型截面，合成型截面都是由基础型截面组成，具体的关系由计算式(4)、(5)、(6)表示。

并非所有截面数据都直接存放在库中，通常一些基础型截面会以合成型截面的形式存放在数据库中。(n, 2n)截面就不仅存放在总散射截面，同时还存放于吸收截面等。对于部分未存放的截面，可以考虑直接将截面值视为0或调用协方差库中截面的值。适用条件是该反应仅高能中子发生且发生概率较小。下面将这两种数据处理方法引入到实际的截面处理中。

辐射俘获截面对反应堆物理计算可引入较大的不确定度，因此，一直都是核数据不确定性分析的重要研究对象。而在WIMS-69截面库中，未直接存放辐射俘获的截面的值。根据式(4)可以计算辐射俘获截面。鉴于(n, 2n)、(n, 3n)、(n, p)与(n, α)反应均为阈能反应，满足前面的处理条件。根据前面的数据处理方法提出两种计算方法，方法1是将这些反应的截面均假定为零，则辐射俘获截面只需将吸收截面中裂变截面的部分去除即可。方法2是协方差数据库${\sigma _{{\rm{2n}}}}$与${\sigma _{{\rm{3n}}}}$为截面库中的${\sigma _{{\rm{2n}}}}$与${\sigma _{{\rm{3n}}}}$。相比方法1，方法2计算得到的辐射俘获截面除去${\sigma _{{\rm{2n}}}}$与${\sigma _{{\rm{3n}}}}$的影响。显然，当核素本身具有(n, 2n)、(n, 3n)反应时，方法2的分析流程结果更加符合截面库中吸收截面与${\sigma _{{\rm{2n}}}}$、${\sigma _{{\rm{3n}}}}$之间的关系。

截面库中的散射截面也是截面库中重要的不确定度来源之一，并通常在截面库中以散射矩阵的形式存在。散射截面中不仅包含${\sigma _{{\rm{else}}}}$与${\sigma _{{\rm{inel}}}}$，还有${\sigma _{{\rm{2n}}}}$与${\sigma _{{\rm{3n}}}}$。由前文可知，${\sigma _{{\rm{2n}}}}$与${\sigma _{{\rm{3n}}}}$可直接参考协方差数据库中的截面值，但即使已知${\sigma _{{\rm{2n}}}}$与${\sigma _{{\rm{3n}}}}$的值，式(5)仍然是一个多元未知函数，无法直接计算出截面初值。

类似于获取${\sigma _{{\rm{2n}}}}$与${\sigma _{{\rm{3n}}}}$的途径，提出散射截面计算方法1，由于非弹性散射反应发生的条件与(n, 2n)、(n, 3n)反应发生的条件相似，同样考虑直接从协方差数据借用${\sigma _{{\rm{inel}}}}$的值，然后再用式(7)求解${\sigma _{{\rm{elas}}}}$。方法2考虑不直接调用协方差数据库中截面值，考虑WIMS-69群截面的数据来源为核评价数据库，则在相同反应道的截面的存储方式应与原核评价数据库中数据的存储方式尽可能保持一致。若协方差中的截面由相同核评价数据库的截面并群而来，假定协方差${\sigma _{{\rm{elas\_cov}}}}$与${\sigma _{{\rm{inel\_cov}}}}$之比与截面库中的${\sigma _{{\rm{else}}}}$与${\sigma _{{\rm{inel}}}}$之比相等，利用式(8)和式(9)求扰动前的${\sigma _{{\rm{else}}}}$与${\sigma _{{\rm{inel}}}}$的初始值。

协方差数据不仅储存了截面自身的不确定度，还描述截面各能群之间的关联性。目前协方差矩阵的数据来源主要分为两种情况，其一为SCALE程序中自带44GROUPCOV模块产生的44群协方差矩阵，通过线性插值的方法将44群转化为分析的截面库的能群数。而SCALE程序中的协方差数据(ZZ-SCALE6.0/COVA-44G)的数据来源：ENDF/ B-Ⅶ、ENDF/B-Ⅵ以及JENDL3.3，包含300多种核素，55种材料，中子能量范围10^-5~20 MeV。其二是借助NJOY程序的ERRORR模块对核评价数据库处理得到所需分析的能群结构的协方差数据。NJOY则可以根据核评价数据库中的协方差信息产生的协方差数据库，具体的核素与截面信息均由使用的核评价数据库决定。不同核评价数据库中拥有协方差矩阵的核素各异，目前普遍使用的是ENDF/B-Ⅶ.1产生的协方差数据，ENDF/B-Ⅶ.1拥有190种材料的协方差数据，并且绝大多数是完成的。其数据来源可以分为三条途径：5大研究机构(BOLNA= Brookhaven- OakRidge- LosAlamos- NRGPetten- Argonne)研究出的一些核素协方差数据；从COMMARA-2.0（先进核反应堆应用的多群协方差矩阵，又称AFCI-2.0 library）参考部分核素的协方差数据；沿用一部分ENDF/B-Ⅶ.0的协方差数据以及参考JENDL4.0中某些次锕系元素的协方差数据^[13]。因此，比较ENDF/B-Ⅶ.1、JEFF3.2以及JENDL4.0三大核评价数据库，ENDF/B-Ⅶ.1具有协方差数据的核素最多，达到了238种；JEFF3.2中有协方差数据的核素总数为218种；JENDL4.0该项数据指标为99种。因此，由NJOY处理各大核评价数据库产生的协方差数据会存在一定的差异。为了验证这种差异给不确定性分析结果带来的影响，选用OECD/NEA设定的不确定性分析建模(UAM)中三哩岛核电厂1号机组(Three Mile Island unit 1, TMI-1)基准题^[14]，利用SUACL程序对不同的协方差数据库进行了具体的分析。

根据两种辐射俘获截面处理方法得到的截面，在基于ENDF/B-Ⅶ.1制作的协方差分析TMI-1基准题在热态满功率(Hot Full Power)条件下得到的无限介质增殖因子K_inf的不确定度结果如表 2所示。

表 2

表 2 扰动不同截面处理方法得到的σr对TMI-1栅元(HFP)中Kinf的不确定度(Δk/k (%)) Table 2 The uncertainty of Kinf (Δk/k (%)) caused by perturbed sr calculated by different methods 核素 Isotope 反应 Reaction 方法1 Method 1 方法2 Mothed 2 UNICORN[15] 235U (n, γ) 0.183 0.183 0.195 238U (n, γ) 0.361 0.364 0.377

表 2 扰动不同截面处理方法得到的σr对TMI-1栅元(HFP)中Kinf的不确定度(Δk/k (%)) Table 2 The uncertainty of Kinf (Δk/k (%)) caused by perturbed sr calculated by different methods

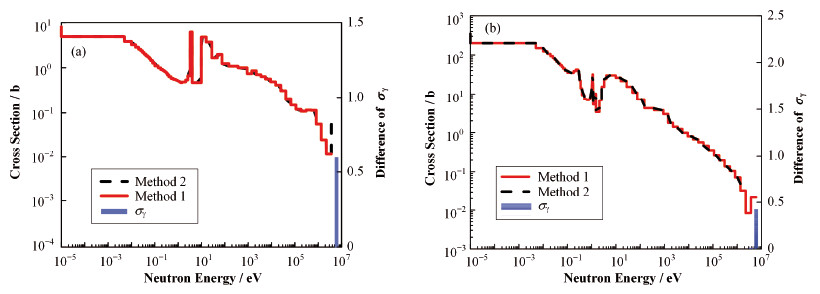
由表 2可知，方法1与方法2得到的不确定性分析结果虽然都很相近，但不确定性分析结果产生了一定的偏差，²³⁸U的导致结果更加显著。对比图 2(a)与图 2(b)，发现²³⁵U的辐射俘获截面在高能区较²³⁸U的辐射俘获截面差别较大，但不确定性分析结果相差更小，主要是因为²³⁸U的辐射俘获截面本身的扰动对不确定度分析结果影响更大，即使不同能群的截面的细微差别也会导致${\sigma _{\rm{r}}}$的不确定度偏差更大。在计算的截面值上，方法2得到截面值在数值上相对方法1的增加了1倍${\sigma _{{\rm{2n}}}}$与2倍${\sigma _{{\rm{3n}}}}$。对应的方法2计算不确定度也大于方法1的结果。以同样采用协方差均为NJOY基于ENDF/B-Ⅶ.1的UNICORN计算结果来看方法2更加接近参考值，由此，分析采用的截面值越与截面实际值接近，计算的不确定度更加可靠。并且在相同扰动下，截面初值越大，则引起的响应的不确定度越大。

图 2

图 2 293 K温度不同方法下238U (a)、235U (b)辐射俘获截面对比 Figure 2 Capture cross section comparison of 238U (a) and 235U (b) calculated by different methods in 293K

基于两种散射截面处理方法得到的散射截面，ENDF/B-Ⅶ.1制作的协方差分析TMI-1基准题热态满功率条件下的无限介质增殖因子(K_inf)的不确定度结果如表 3所示。

表 3

表 3 扰动不同截面处理方法的σelse与σinel对TMI-1栅元(HFP)中Kinf的不确定度(Δk/k (%)) Table 3 The uncertainty of Kinf (Δk/k (%)) caused by perturbed selse and σinel calculated by different methods 核素 Isotope 反应 Reaction 方法1 Method 1 方法2 Method 2 TSUNAMI-1D CASMO-4%[1] 235U (n, elas) 3.43×10-4 6.60×10-4 4.07×10-4 — 235U (n, inelas) 7.87×10-4 3.88×10-4 — — 238U (n, elas) 3.51×10-2 6.22×10-2 2.90×10-2 3.94×10-2 238U (n, inelas) 7.37×10-2 3.98×10-2 — — 1H (n, elas) 3.68×10-2 3.68×10-2 2.63×10-2 2.74×10-2

表 3 扰动不同截面处理方法的σelse与σinel对TMI-1栅元(HFP)中Kinf的不确定度(Δk/k (%)) Table 3 The uncertainty of Kinf (Δk/k (%)) caused by perturbed selse and σinel calculated by different methods

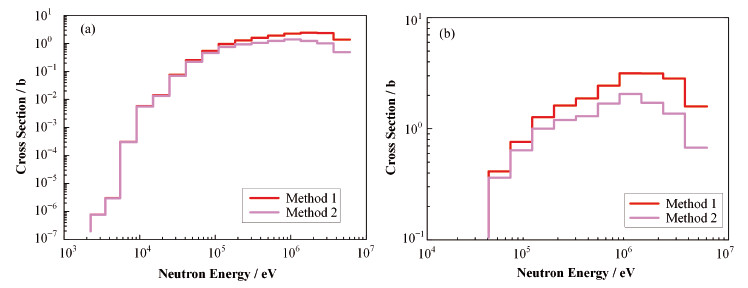
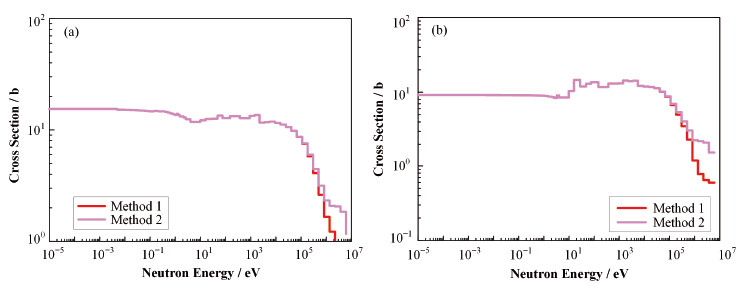
由表 3可知，两种方法计算的结果在同一数量级，而在弹性散射与非弹性散射截面所引起的计算结果的大小却相反。方法1得到的非弹性散射截面引起的不确定度大于方法2，而方法二弹性散射截面引起的不确定度大于方法1。由于总散射截面在计算截面时为常量，方法1中非弹性散射截面直接调用协方差矩阵中的值，比方法2中采用按照协方差中弹性散射截面与非弹性散射截面的比例得到的非弹性散射截面要大，正如图 3所示，差异主要表现在高能区。而弹性散射截面小于方法2，能群截面比较如图 4。这种数值上的差异在²³⁵U还是²³⁸U均是如此。这也说明截面初值越大，在扰动一定时，引入的不确定度越大。而¹H的弹性散射计算结果保持不变，因为¹H没有非弹性散射截面。对比参考值，方法1中的计算结果更加靠近。这也说明相同数据来源的截面库与协方差数据中截面的理论值是近似的。而方法1计算的截面在理论本身是更接近截面库中理论值。

图 3

图 3 293K温度下不同方法计算235U (a)、238U (b)非弹性散射截面对比 Figure 3 Inelastic scattering cross section comparison of 235U (a) and 238U (b) calculated by different methods in 293K

图 4

图 4 293K温度下不同方法计算235U (a)、238U (b)弹性散射截面对比 Figure 4 Elastic scattering cross section comparison of 235U (a) and 238U (b) calculated by different methods in 293K

当进行数据处理来求取截面时，都应保证扰动的截面值的计算方法与截面库界面存放的规律保持一致，才能让不确定性分析的结果更加可靠。同时，在扰动一定的条件下，截面初值越大，引入给同一响应的不确定度更大。因此，在常规压水堆的反应堆物理计算的不确定性分析中，辐射俘获截面的计算适合采用辐射俘获截面处理方法2，而散射截面的计算适合采用散射截面处理方法1。

为了验证不同数据库的协方差数据给截面不确定性分析带来的影响，在自主开发的SUACL截面不确定性分析程序上，依次验证三大核评价数据库产生的协方差数据。因为²³⁸U三个核评价数据库均有协方差数据的核素，以²³⁸U作为分析核素，分析的反应道为裂变反应与辐射俘获反应。讨论在HFP条件下，²³⁸U裂变截面与辐射俘获截面所引入的K_inf不确定度，计算结果由表 4给出，各核评价数据库的协方差数据库中的截面分布见图 5。

表 4

表 4 基于不同协方差数据库，扰动238U裂变截面与辐射俘获截面下TMI-1栅元(HFP)中Kinf的不确定度(Δk/k (%)) Table 4 The uncertainty of Kinf (Δk/k (%)) caused by perturbed 238U σf and σr by using different covariance database in TMI-1 cell 协方差Covariance ENDF/B-Ⅶ.1 JENDL4.0 JEFF3.2 (n, f) 0.0152 0.173 0.000071 8 (n, γ) 0.364 0.380 0.522 注：参考值（fission/Kinf的不确定度/%）：TSUNAMI-1D: 0.0152%, CASMO-4: N/A, UNICORN: 0.0147%；参考值（capture/Kinf的不确定度/%）：TSUNAMI-1D: 0.279%, CASMO-4: 0.325%, UNICORN: 0.377% Notes: Reference value (uncertainty of fission/Kinf): TSUNAMI-1D: 0.0152%, CASMO-4: N/A, UNICORN: 0.0147%; reference value (uncertainty of capture/Kinf): TSUNAMI-1D: 0.279%, CASMO-4: 0.325%, UNICORN: 0.377%

表 4 基于不同协方差数据库，扰动238U裂变截面与辐射俘获截面下TMI-1栅元(HFP)中Kinf的不确定度(Δk/k (%)) Table 4 The uncertainty of Kinf (Δk/k (%)) caused by perturbed 238U σf and σr by using different covariance database in TMI-1 cell

图 5

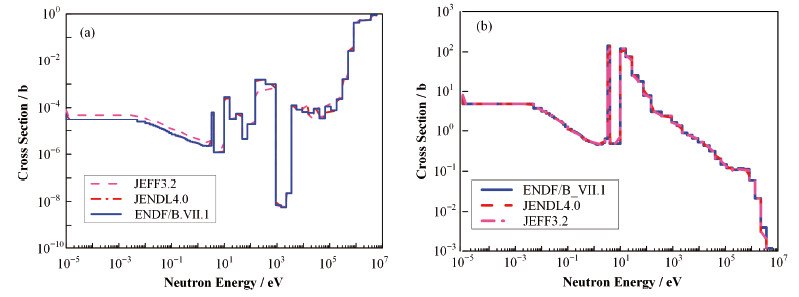
图 5 三大核评价数据库的协方差数据库中238U的裂变截面(a)和辐射俘获截面(b)变化趋势 Figure 5 Variation tendency of 238U fission cross section (a) and capture cross section (b) obtained from covariance libraries of three evaluated nuclear database

由表 4可知，无论是裂变截面还是辐射俘获截面，采用由NJOY在ENDF/B-Ⅶ.1数据库与JENDL4.0数据库下产生的协方差数据更为接近，并且计算结果与参考值更为符合。其中原因可以从以下几个方面解释：TSUNAMI-1D与CASMO-4所采用的协方差是基于ENDF/B-Ⅶ、ENDF/B-Ⅵ以及JENDL3.3制作的，截面的不确定度是由其协方差数据决定，因此，基于ENDF/B-Ⅶ.1与JENDL4.0的协方差计算的不确定度与参考值更相符。而基于JEFF3.2制作的协方差所计算结果会与前两者差别较大，主要是由库中协方差截面差别所致。由图 5(a)可知，由ENDF/B-Ⅶ.1与JENDL4.0得到的协方差库中的中子裂变截面无论是热区还是共振能群几乎是完全重合，只有高能区部分裂变截面有较显著的差异。但JEFF3.2产生协方差数据库的裂变截面在热区与共振能区与其他两个数据库中存在明显的差异。截面之间差异较大时，对相应传递的不确定度也差异较大。在辐射俘获反应道上，三者计算的不确定度相较裂变反应道的更加接近，这与能谱差异相符。在图 5(b)中，基于三大核评价数据库的协方差数据库中辐射俘获的截面差异比三者在裂变截面上差异更小，只有高能区能量范围为10⁶~10⁷截面的差异略微较大，其他区域ENDF/B-Ⅶ.1的协方差与JENDL4.0的协方差截面值更加符合。

压水堆中其他重要核素反应道的不确定性分析结果由表 5展示。由于核评价数据中部分核素协方差数据不全，因此，只描述了在基于含有核素协方差数据的核评价数据制作的协方差数据下分析的结果，并以SAINT与UNICORN计算的结果以作为参考值。

表 5

表 5 基于不同协方差数据库，扰动235U的裂变、辐射俘获截面与1H辐射俘获截面下，TMI-1栅元(HFP)中Kinf的不确定度(Δk/k (%)) Table 5 The uncertainty of Kinf (Δk/k (%)) caused by others important perturbed cross section of 235U and 1H by using different covariance database in TMI-1 cell 核素Nuclides 反应Reaction ENDF/B-Ⅶ.1 JENDL4.0 JEFF3.2 235U (SUACL) (n, f) 0.084 0.089 N/A 235U (SAINT[4]) (n, f) 0.095 0.101 N/A 235U (SUACL) (n, γ) 0.209 0.157 N/A 235U (SAINT[4]) (n, γ) 0.194 0.157 N/A 1H (SUACL) (n, elas) 0.037 N/A 0.037 1H (UNICORN[15]) (n, elas) 0.035 N/A N/A

表 5 基于不同协方差数据库，扰动235U的裂变、辐射俘获截面与1H辐射俘获截面下，TMI-1栅元(HFP)中Kinf的不确定度(Δk/k (%)) Table 5 The uncertainty of Kinf (Δk/k (%)) caused by others important perturbed cross section of 235U and 1H by using different covariance database in TMI-1 cell

与参考程序SAINT、UNICORN的分析结果相比，SUACL程序的结果均符合较好，说明SUACL计算结果具有较好的可靠性。比较²³⁵U两种反应道，无论是SUACL还是SAINT分析的²³⁵U裂变截面不确定度，采用JENDL4.0协方差分析的不确定度要略微大于ENDF/B-Ⅶ.1的，相反，²³⁵U的辐射俘获截面计算的不确定度在ENDF/B-Ⅶ.1的协方差下数值更大。¹H的弹性散射截面由ENDF/B-Ⅶ.1与JENDL4.0产生的协方差数据下两者计算结果相同，且与参考值相比也非常接近。说明不同核评价数据库中协方差数据虽可能存在相同之处，但也存在不可忽视的差别。

由以上结果分析可知，基于不同核评价数据库制作的协方差下，虽各反应道的结果比较接近，但测量的不确定度仍然存在一定的差异。不同的核评价数据库中所含有协方差信息并不完全一致，在不确定性分析中选用协方差矩阵时，要根据实际的堆型问题的需要，合理挑选适用的核评价数据库下得到的协方差矩阵。

围绕核数据的不确定性分析，本文采用统计抽样法来分析截面初值的一致性与协方差数据对核数据不确定性分析结果的影响。通过分析截面一致性与协方差数据结果可知，计算的不确定度均与参考值符合较好，表明自主开发的程序SUACL对核数据不确定性分析具有较高的可靠性。而采用不同的初值计算方法得到的截面引入的不确定度确实存在一定偏差。具体表现为：在近似求解某些截面时，在相同的扰动条件下，截面值越大，对输出响应引入的不确定度越大，而不确定度的偏差大小由该反应道所引起的不确定度大小决定。比较²³⁵U、²³⁸U的辐射俘获反应道的不确定性分析结果，²³⁸U引入不确定度相对²³⁵U要大，即使²³⁸U截面差别小于²³⁵U，但这种不确定度的偏差²³⁸U比²³⁵U的波动更加明显。主要是²³⁸U辐射俘获截面引入的K_inf不确定度比²³⁵U辐射俘获截面引入的不确定度要大。因此，截面本身的不确定度以及截面的初值都是影响分析响应不确定度的重要因素。而观察不同截面计算方法的结果，得出无论是何种反应道截面，都应保证计算扰动前的截面值要符合截面库中截面存储的原则，才能让不确定性分析的结果更加可靠。

协方差数据对于不确定性分析结果影响较为显著，原因在于截面的不确定度的信息都直接存储到相关的协方差矩阵中。对比核评价数据库产生的协方差数据，对同一反应道的分析结果，发现扰动²³⁸U的裂变截面与辐射俘获截面，虽在JENDL4.0协方差数据库下得到的不确定度与ENDF/B-Ⅶ.1的协方差结果比较接近，但与JEFF3.2的协方差计算不确定度有较大的差别。而且JENDL4.0协方差数据库计算的不确定度会大于在ENDF/B-Ⅶ.1的结果。对于²³⁵U的裂变反应道上，同样ENDF/B-Ⅶ.1与JENDL4.0的协方差计算的不确定度比较接近，JENDL4.0协方差数据库计算的不确定度大于在ENDF/B-Ⅶ.1的结果。而²³⁵U的辐射俘获截面则完全相反，在JENDL4.0协方差数据计算的不确定度会小于在ENDF/B-Ⅶ.1的分析的结果。说明不同评价数据库下制作的协方差数据彼此之间并不相同。因此，若考虑实际核电站性能与安全评价时，对于中子截面引起的核反应堆物理的不确定性分析应该从实际堆型出发，找到适合于实际堆型的核评价数据库制作的协方差，才能使得计算结果更加精准与可靠。