2. 中国科学院大学 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
熔盐堆在运行过程需要不断地去除中子吸收截面较大的气态裂变产物,如氪、氙、氚等[1]。目前熔盐堆脱气系统的研究是在美国橡树岭国家实验室(Molten Salt Reactor Experiment, MSRE)设计基础上展开的[2-3],其中脱气的主要过程是通过气泡发生器注入载气体并碎化形成粒径均匀的微气泡,然后经过传质过程吸收裂变产生的裂变气体,最后通过脱气回路中的分离器从熔盐中分离富含裂变产物的载气气泡,从而达到连续从熔盐燃料中去除氪、氙、氚的目的。气泡发生器作为熔盐堆脱气系统中的关键设备,其产生气泡的大小和均匀程度直接影响到系统的脱气效率,而文丘里气泡发生器因其结构简单、能够有效地产生均匀粒径的微气泡等优点,而被熔盐堆脱气系统采用。
文丘里气泡发生器产生气泡的原理,是通过扩散段的紊流作用打碎通入喉部的气体而产生[4]。1955年,Hinze[5]就开展了湍流场中气泡破碎的理论研究。目前针对文丘里气泡发生器也已开展了流量参数、结构参数等相关参数与气泡碎化的研究,同时取得了许多研究成果[6-11]:气泡从喉部流出后会经历减速形变以及碎化过程,而气泡碎化主要发生在扩张段;在扩张段入口处,流场的压力梯度出现峰值,并且此处湍动能较大,可能是造成气泡在扩张段碎化的原因;扩张段处扩张角的大小是影响气泡碎化后尺寸大小的关键因素等。然而,由于文丘里气泡发生器中气液两相流动以及气泡的碎化过程十分复杂,并且目前的研究结果没有给出气泡在管道中的速度分布与碎化之间的关系,所以本文在熔盐堆脱气系统水力试验台架的实验基础上,针对气泡在文丘里气泡发生器喉部以及扩张段处的具体运动、碎化以及碎化前后气泡粒径大小的情况展开研究,来探究气泡在喉部和扩张段的速度分布与气泡发生碎化的关系。
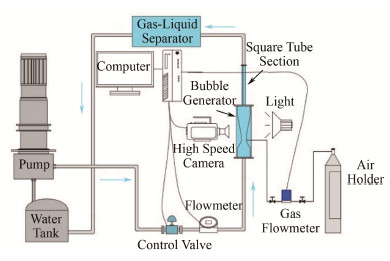
1 实验系统与流程 1.1 实验系统实验系统包括主回路系统、供气系统、高速摄像系统以及控制系统组成,实验回路如图 1所示。主回路系统包括实验段、储水箱和循环泵。水箱中的去离子水通过泵的驱动进入到文丘里气泡发生器中,储气钢瓶中的氩气进入到文丘里气泡发生器的喉部与水混合形成较大的气泡,然后流经扩张段碎化成较小的气泡,随后分别流经观测段和气液分离器,最终流回水箱。观测段是用来观测氩气流经文丘里气泡发生器后碎化后的气泡大小,气泡分离器用于将水中的氩气从回路中去除。为方便观测和记录气泡的碎化和运动情况,回路中的气泡发生器,观测段及气泡分离器是由透明有机玻璃材料制成。
|
图 1 试验系统回路图 Figure 1 Schematic diagram of the experimental system |
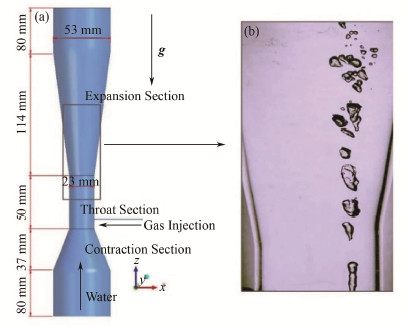
试验段文丘里气泡发生器的具体结构尺寸如图 2所示。文丘里气泡发生器由圆柱形入口段、圆锥形收缩段、圆柱形喉部、圆锥形扩张段、圆柱形出口段以及喉部的进气支管组成。其中实验中采用的文丘里气泡发生器喉部的进气孔径有三组,分别为1.5 mm、2.0 mm、2.5 mm。
|
图 2 文丘里式气泡发生器结构尺寸图 Figure 2 Structure dimention figure of the Venturi-type bubble generator |
实验的主要目的就是观测和记录喉部和扩张段处的气泡运动、碎化以及与水相的相互作用情况等。具体试验流程,首先通过计算机控制泵以及主回路上的流量控制阀来控制文丘里气泡发生器的入口水流量,实验中水流量设置分别为5 m3·h-1、8 m3·h-1、14 m3·h-1、20 m3·h-1。然后打开储气钢瓶阀门,利用北京七星华创电子公司生产的型号为cs200、测量范围0~2000 mL·min-1、工作压力0~3 MPa的氩气气体质量流量计来控制进入到文丘里气泡发生器喉部的氩气流量,流场氩气体积含气率为0.2%。每组实验中在使用美国Vision Research公司生产的型号V-1210高速摄像机拍摄记录前要保证流场至少稳定20 min。在本文中高速相机拍摄记录图像帧率为20000帧/秒,分辨率为512x800像素,曝光时间为4.19 μs。同时发光二极管(Light Emitting Diode, LED)灯放置在文丘里管的另一侧。本实验中高速相机拍摄记录的各组实验工况设置如表 1所示。
| 表 1 各组实验工况 Table 1 Experiment conditions |
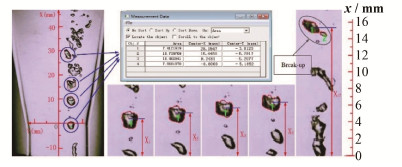
在进行气泡速度统计时,由于气泡并不是规则球体,因此在统计气泡的位置时本文中采用气泡在平面中像素加权后的质心位置作为气泡在该时刻的位置,如图 3所示。
|
图 3 数据处理过程 Figure 3 Processing of data analysis |
为了数据统计方便,本文将喉部与扩张段的交接处定义为参考点,即x=0 mm。同时每隔5张图片统计一次单个气泡的质心位置,即每隔0.00025 s量取气泡移动的距离。由于时间间隔较小,因此可以近似认为在0.00025 s内气泡是匀速运动,这样就可以得到某一位置的气泡速度大小:
| ${v_{{x_n}}} = \frac{{{x_{n + 1}} - {x_n}}}{{\Delta t}}$ | (1) |
式中:
为了更直观显示气泡速度在文丘里气泡发生器的变化情况,以及分析气泡碎化的原因,我们将气泡的速度与无进气条件下流场中水流速度的变化情况进行对比。由于实验中难以直接测得水流速度在某一轴向位置上的连续变化情况,因此通过计算机数值模拟的方法来得到水流速度在文丘里管中的变化情况。
首先建立如图 4所示的喉部无进气支管,且与实验中所采用的文丘里管尺寸比例为1:1的三维计算模型,然后进行网划分,得到三套不同尺度的网格模型,网格数分别是a: 1168638、b: 1587707、c: 2219192。
|
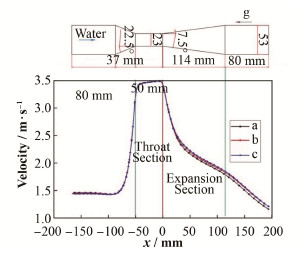
图 4 不同网格密度流场中速度分布对比 Figure 4 Comparison of the velocity distribution from different grid densities |
分别对上述三种不同尺度的网格模型进行计算,计算边界条件如下:采用速度入口边界条件,入口速度为0.63 m·s-1即入口水流量为5 m3·h-1,出口采用压力出口边界条件,出口压力由实验测得,其值为2.5×104 Pa。计算得到在无进气情况下管内水流速度在平行于文丘里气泡发生器轴向,并且距离中心轴6.6 mm处的压强和速度分布如图 4所示,此处约为气泡运动的路径。可以看出,a网格所得计算结果与b网格的计算结果有一定的误差,而b、c网格的计算结果较为吻合,所以采用b尺度的网格模型就可以得到较准确的水流速度在文丘里管中的变化情况。因此,本文中不同流量水流速度在文丘里管中的变化情况都将采用b尺寸的网格模型来计算。
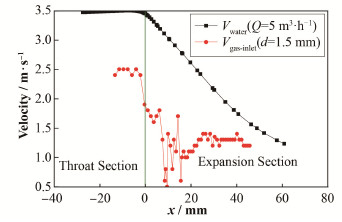
2 结果与讨论 2.1 喉部与扩张段处的气泡速度变化情况图 5是水流量为5 m3·h-1、进气孔径为1.5 mm时的喉部与扩张段处气泡速的变化情况与无进气条件下流场中水流速度的变化情况对比图。从图 5可以看出,气泡的运动可以分成4个明显不同阶段:第一阶段,当-20 mm < x < 0 mm时,气泡高速稳定运动阶段;第二阶段,当0 mm < x < 20 mm时,气泡速度剧烈变化阶段;第三阶段,当20 mm < x < 40 mm时,气泡速度稳定波动阶段;第四阶段,当40mm < x < 50 mm时,气泡低速稳定运动阶段。
|
图 5 水流量为5 m3·h-1、进气孔径为1.5 mm时气泡速度分布与无进气条件下流场中水流速度分布对比 Figure 5 Comparison of bubble velocity distribution with water velocity distribution without gas inlet under condition of Qwater= 5 m3·h-1, dgas-inlet=1.5 mm |
在第一阶段中,由图 5可以看出,在文丘里管喉部产生的气泡速度较大,且气泡流速较为稳定。但是与无进气条件下的该处水流速度相比气泡速度明显偏小,如此明显的气液两相的速度差并没有使得此处气泡迅速碎化成小的气泡,如图 6所示。分析其原因如下,首先在水流量为5 m3·h-1、进气量为167 mL×min-1、进气孔径为1.5 mm的条件下,通过换算,可以得到进入到喉部的氩气具有一个约为1.6 m·s-1的初速度;同时,实验中测得文丘里气泡发生器喉部压力约为2.1x104 Pa,进气支管处的压力为3.0x104 Pa,这就使得氩气更容易进入到文丘里管喉部。其次,实验中观察到氩气通过注气孔进入文丘里管喉部时,并没有立即形成一个个独立的球形气泡,而是以细长的气泡柱的形式存在,随着气柱向上运动,在强烈的气液两相的相互作用以及表面张力的作用下,气柱开始断裂形成独立的气泡,但此时气体仍以细长的气体柱形式存在,随着气体的不断向上运动,气柱开始收缩形变成偏球状的气泡,而在此过程中气泡柱的横截面较小,使得气泡与液体水在横向上产生的相互作用较小。而在流动方向上气液相互作用的面积较大。喉部的氩气迅速增大到约为2.5 m·s-1,同时也可以推测出在-20mm < x < 0 mm阶段中气泡周围的流场较为稳定,其流场速度也约为2.5 m·s-1。因此气泡流速在该阶段较为稳定。最后小气柱变为球形气泡主要是在靠近x=0 mm附近,在喉部气泡没有发生剧烈的形变和碎化。
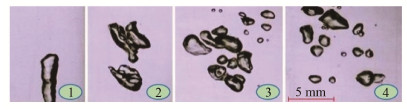
|
图 6 气泡运动的4个阶段 Figure 6 Four stages of bubble motion |
第二阶段中,气泡的速度发生剧烈的变化,这种变化首先是速度迅速变小,然后气泡速度无规律的波动。造成这种现象的原因是进入到扩张段时管径加大,流场速度变小,由于氩气和水的性质不同并且氩气泡所受惯性力较小,使得流场中氩气泡的速度减小更为明显,同时流场从相对稳定的流场转变成强烈的湍流场[12]。在该阶段气液两相的速度差造成了气泡和水发生较强的相互作用,气泡开始发生形变、破碎成小的气泡,并伴随着与相邻气泡的相互作用,所以该阶段的气泡速度波动较大。
在第三阶段,大气泡已经由第二阶段碎化成了较小的气泡,但是该阶段气泡的速度仍然不稳定,原因是在20 mm < x < 40 mm处流场不稳定,水流量为5 m3·h-1工况下湍流强度并不是特别强烈,因此气泡在该处的速度波动不是很剧烈,但是在该区域内气泡会进一步碎化形成更小的气泡。经过前面两个阶段后气泡已经基本碎化形成较为稳定大小的气泡并且流场也趋于稳定,因此在第四阶段中气泡能够保持低速稳定地运动。
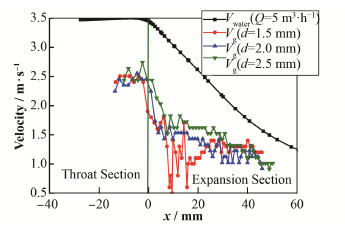
2.2 不同进气孔径,喉部与扩张段处的气泡速度变化情况图 7是水流量为5 m3·h-1,进气孔径分别为1.5mm、2.0 mm、2.5 mm时的喉部与扩张段处气泡
|
图 7 水流量为5 m3·h-1,进气孔径分别为1.5 mm、2.0 mm、2.5 mm时气泡速度分布与无进气条件下流场中水流速度分布对比 Figure 7 Comparison of bubble velocity distribution with water velocity distribution without gas inlet under condition of Qwater=5 m3·h-1, dgas-inlet=1.5 mm, 2.0 mm, 2.5 mm |
速度的变化情况与无进气条件下流场中水流速度的变化情况对比。通过分析我们仍然能够将气泡速度在喉部和扩张段处的变化情况分成上述4个阶段。且通过对比不同进气孔径形成的气泡在喉部与扩张段处的速度分布情况我们发现,随着进气孔径的增大,气泡的在4个阶段的稳定性增加,尤其是在气泡主要碎化的第二和第三阶段。从图 8可以看出,造成这一现象的原因是进气孔径越大,文丘里气泡发生器喉部形成的独立气泡的体积越小。
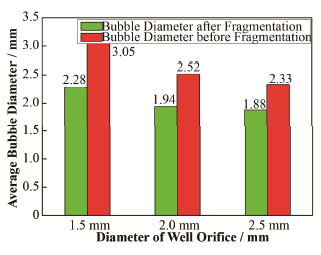
|
图 8 不同进气孔径气泡破碎前的平均粒径和破碎后的平均粒径的对比 Figure 8 Comparison of average bubble size before and after bubble breakup with different gas inlet |
进气孔径大时喉部形成的气泡较小,因而气泡在第二阶段的速度变化的剧烈程度降低,这也使得气泡的形变程度和碎化程度减小。总之在喉部形成的气泡越小,气泡在0 mm < x < 40 mm处形状越稳定,剪切相互作用等也越小,气泡的碎化程度也越小,因而气泡速度的不稳定性减小。
定义气泡的碎化率如下,即碎化前气泡平均直径减去气泡破碎后平均直径,然后比上碎化前气泡平均直径:
| $Fra = \frac{{{D_{\rm{b}}} - {D_{\rm{a}}}}}{{{D_{\rm{b}}}}} \times 100\% $ | (1) |
式中:
对图 8中不同进气孔径条件下的气泡碎化率分别进行计算得到,当管道中水流量为5 m3·h-1,进气孔径为1.5 mm、2.0 mm、2.5 mm时,气泡的碎化率分别为25.25%、23.01%、19.31%。所以在相同的流量情况下,随着喉部进气孔径的增大,气泡碎化率减小,也就是说气泡碎化的剧烈程度降低。因此我们同样可以得出这样的结论:进气孔径的增大,气泡在4个阶段的稳定性增加。
2.3 不同工况下,气泡在各个位置的变化情况通过上面的分析知道,当水流量为5 m3·h-1时,气泡在0 mm < x < 20 mm处是速度剧烈变化阶段,气泡在该阶段速度迅速减小,气液两相的强烈相互作用等使得气泡开始发生形变、碎化。图 9是水流量分别为8 m3·h-1、14 m3·h-1、20 m3·h-1,进气孔为1.5mm时扩散段的气泡变化情况。从图 9中可以明显看到,气泡在刚进入到扩散段时,气泡形状发生强烈的变化,同时气泡开始破碎,并且主要的破碎区域仍然在0 mm < x < 20 mm。然而随着液体流量的增加,该破碎区域会向着靠近x=0 mm的位置逐渐缩小,即液体流量的增加,气泡主要碎化区域范围会向着靠近x=0 mm的位置逐渐缩小。

|
图 9 水流量分别为8 m3·h-1、14 m3·h-1、20 m3·h-1,进气孔为1.5 mm时扩散段的气泡变化情况 Figure 9 Bubble motion in expansion section (Qwater=8 m3·h-1, 14 m3·h-1, 20 m3·h-1, dgas-inlet=1.5 mm) |
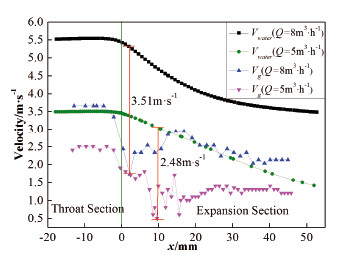
图 10是入口水流量分别为5 m3·h-1、8 m3·h-1,进气孔径为1.5 mm时的喉部与扩张段处气泡速的变化情况对比,以及对应流量下水流速度的变化曲线。当液体流速分别为5 m3·h-1、8 m3·h-1时,对应水流量条件下的气泡速度与水流速度的最大差值分别为2.48 m·s-1、3.51m·s-1,即液体流速增加到8m3·h-1后,气泡在进入扩张段时的速度梯度增大,气液间的相互作用更加剧烈,所以气泡在第二阶段的碎化程度增强。而且随着入口水流量的增加,流场在第三阶段的湍流强度也增强,使得气泡速度在该阶段的波动增大,可以推测气泡在该阶段的碎化程度增强,但是与第二阶段的气泡碎化相对比,仍然可以断定气泡的主要碎化区域还是在第二阶段。
|
图 10 水流量分别为5 m3·h-1、8 m3·h-1,进气孔径为1.5 mm时气泡速分布 Figure 10 Bubble velocity distribution under condition of Qwater=5 m3·h-1, 8 m3·h-1, dgas-inlet=1.5 mm |
基于熔盐堆脱气系统水力试验台架的实验基础上,采用高速摄像的方法,研究了气泡在文丘里气泡发生器喉部以及扩张段处的运动和碎化情况,分析了气泡在喉部和扩张段的速度分布与气泡发生碎化的关系,得到以下结论:
1) 气泡在文丘里气泡发生器的喉部和扩张段入口处的运动可以分为4个阶段:第一阶段,气泡高速稳定运动阶段;第二阶段,气泡速度剧烈变化阶段;第三阶段,气泡速度稳定波动阶段;第四阶段,气泡低速稳定运动阶段。其中气泡的碎化过程主要是在第二阶段发生的。
2) 当进气孔径的增大,文丘里气泡发生器喉部形成的独立气泡体积将会减小,气泡在进入到扩张段时形变和碎化程度降低,气泡的碎化率减小,同时气泡在4个阶段的稳定性增加。
3) 随着液体流量的增加,气泡主要碎化区域范围会向着靠近x=0 mm的位置逐渐缩小,即碎化区域会向着靠近喉部与扩张段交界位置缩小,并且气泡在第三阶段的碎化程度增强。
| [1] |
Robertson R C. MSRE design and operation report I[R]. ORNL-0728, U.S. Atomic Energy Commission, 1965: 205-243.
|
| [2] |
Robertson R C. Two-fluid molten-salt breeder reactor design study[R]. ORNL-4528, U.S. Atomic Energy Commission, 1970.
|
| [3] |
Robertson R C. Conceptual design study of a single-fluid molten-salt breeder reactor[R]. ORNL-4541, U.S. Atomic Energy Commission, 1971.
|
| [4] |
唐文偲, 阎昌琪, 孙立成, 等. 文丘里式气泡发生器气泡碎化特性研究[J]. 原子能科学技术, 2014, 48(5): 844-848. TANG Wencai, YAN Changqi, SUN Licheng, et al. Characteristics of bubble breakup in venturi-type bubble generator[J]. Atomic Energy Science and Technology, 2014, 48(5): 844-848. |
| [5] |
Hinze J O. Fundamentals of the hydrodynamic mechanism of splitting in dispersion processes[J]. American Institute of Chemical Engineers, 1955, 1(3): 289-295. DOI:10.1002/(ISSN)1547-5905 |
| [6] |
Cottrell W B. Operation of aircraft reactor experiment[R]. ORNL-1854, U.S. Atomic Energy Commission, 1955.
|
| [7] |
居晓峰, 孙立成, 唐文偲, 等. 文丘里式气泡发生器工作特性分析[J]. 核技术, 2014, 37(12): 120605. JU Xiaofeng, SUN Licheng, TANG Wencai, et al. Analysis of the operating characteristics of a Venturi-type bubble generator for MSR[J]. Nuclear Techniques, 2014, 37(12): 120605. DOI:10.11889/j.0253-3219.2014.hjs.37.120605 |
| [8] |
Kaneko A, Nomura Y, Takagi S, et al. Bubble break-up phenomena in Venture tube[J]. The Japan Society of Mechanical Engineers (B), 2012, 2(78): 207-217. |
| [9] |
莫政宇, 杜敏, 孙立成, 等. 底含气率条件下文丘里管气泡发生器内气泡碎裂过程研究[J]. 核动力工程, 2016, 37(6): 41-44. MO Zhengyu, DU Min, SUN Licheng, et al. Investigation on bubble breakup in a Venturi-tube bubble generator under low gas fraction condition[J]. Nuclear Power Engineering, 2016, 37(6): 41-44. |
| [10] |
Yu X, Felicia P. Optimization of cavitation venturi tube design for pico and nano bubbles generation[J]. International Journal of Mining Science and Technology, 2015, 25(4): 523-529. DOI:10.1016/j.ijmst.2015.05.002 |
| [11] |
Li J J, Song Y C, Yin J L, et al. Investigation on the effect of geometrical parameters on the performance of a Venturi type bubble generator[J]. Nuclear Engineering and Design, 2017, 325: 90-96. DOI:10.1016/j.nucengdes.2017.10.006 |
| [12] |
Azad R S. Turbulent flow in a conical diffuser:a review[J]. Experimental Thermal and Fluid Science, 1996, 13(4): 318-337. DOI:10.1016/S0894-1777(96)00091-X |


