2. 中国科学院大学 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
无论环形正负电子对撞机为提高对撞亮度,还是高能同步辐射光源为提高亮度,都追求多束团、高流强运行[1-2]。束流通过高频腔和束流管道时,由于高次模与阻抗壁的影响而产生的耦合束团不稳定性必将限制流强的提升。因此,加速器需要设计横向或纵向逐束团反馈系统。反馈系统为束团产生一个合适的反馈校正信号,该信号再提供给冲击器(Kicker)作用到该束团,冲击器处的相位与束流位置监测器(Beam Position Monitor, BPM)处的相位成90°差[3],可采用最小二乘法或选择滤波器法,设计有限长单位冲激响应(Finite Impulse Response, FIR)滤波器来获得该反馈校正信号。深入研究这两种方法的差异,并比较在横向反馈系统和纵向反馈系统中处理的差别,为反馈系统选择更合适的滤波器设计方法。另外,无论横向工作点还是纵向工作点在加速器工作时会有一定漂移,进而影响FIR滤波器的工作,所以,需要优化滤波器算法,设计具有一定工作带宽且可靠的滤波器。
1 加速器逐束团数字反馈系统束流在高频腔和束流管道中运行,前面的束团会受到高次模与阻抗壁的影响而产生尾场[4],尾场反作用于后续的束团,产生耦合束团不稳定性,这必将限制流强的提升,甚至会使束流质量变差和丢失。所以,采用逐束团反馈系统来抑制耦合束团不稳定性。
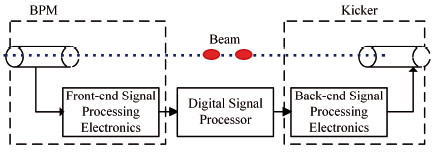
逐束团数字反馈系统如图 1所示[5],是由拾取电极BPM、前端信号处理电子学、数字信号处理电子学、后端信号处理电子学以及冲击器等部分组成。首先拾取电极BPM获取束流信号,经由前端信号处理电子学处理,再传输给数字信号处理电子学,经过反馈算法计算出反馈所需的校正信号,输出给后端信号处理电子学。最后,由冲击器产生校正力作用于相应束团。
|
图 1 逐束团数字反馈系统 Figure 1 Diagram of digital bunch-by-bunch feedback system |
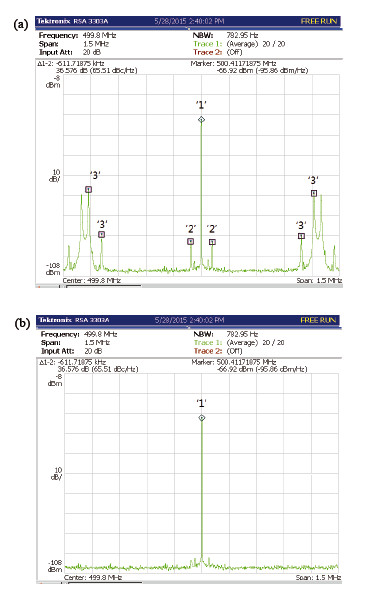
加速器储存环中束流频谱图如图 2所示,图 2(a)是启动反馈系统前束流的频谱图,图中标号‘1’对应的分量是直流分量,对应于加速器束流回旋频率;‘2’是加速器纵向工作点,对应于加速器纵向振荡的频率;‘3’是加速器横向工作点,对应于加速器横向振荡的频率;图 2(b)是启动反馈系统后束流的频谱图,表明束流经反馈系统后,纵向振荡和横向振荡得到有效消除抑制。
|
图 2 启动反馈系统前(a)、后(b)束流的频谱图 Figure 2 Spectrum of the beam before (a) and after (b) the feedback system is opened |
为了得到所需的反馈校正力,需要提取与反馈相关振荡信号,滤除直流分量,抑制与该反馈无关的振荡信号,同时对提取出的信号移相,该过程可采用滤波器来实现。与模拟滤波器相比,FIR滤波器更灵活、方便,因而受到越来越多的加速器实验室青睐。
2 反馈系统中FIR滤波器的设计 2.1 FIR滤波器基本原理在逐束团反馈系统中,需先将逐束团的数字信号分离成单束团的逐圈信号,再将单束团的逐圈信号输入FIR滤波器,乘以相应滤波器系数,计算出反馈所需的校正信号。FIR滤波器基本原理表达式:
| $ y[n] = \sum\limits_{k = 0}^N {{a_k}} {x_{n -k}} $ | (1) |
式中:xk是n号束团第k圈输入数据;y[n]是n号束团校正信号;ak是FIR滤波器系数;N+1是滤波器阶数。
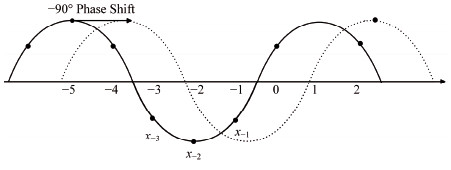
反馈信号处理前后相位变化如图 3所示,滤波器系数可通过选择滤波器法和最小二乘法得到。
|
图 3 反馈信号处理前后相位变化情况 Figure 3 Phase variation of the feedback signal before and after processing |
储存环中,理想束团的k圈位置信号表达式[6]:
| $ x(k) = \sum\limits_{m = 0}^M {{A^{(m)}}} \sin (k{\phi ^{(m)}} + {\Delta ^{(m)}} + {\psi ^{(m)}}) $ | (2) |
式中:m表示运动的方向,m=0是直流偏移;A(m)是幅值;ϕ(m)表示每圈相位偏移;ψ(m)表示补偿相位;Δ(m)为每圈由于工作点偏移引起的相位偏移。
将最小二乘法应用到反馈系统算法中的理念是由日本同步辐射光源科学家Nakamura提出[7],其原理:让束团的k圈理想位置x[-k]与束团的k圈真实位置x-k之差的平方和最小,即S最小:
| $ S = \sum\limits_{k = 1}^N {{{(x[-k] -{x_{ -k}})}^2}} $ | (3) |
可得,FIR滤波器的各阶系数:
| $ \begin{array}{c} {a_k} = \sum\limits_{m = 0}^M {{G^{(m)}}} ({{\boldsymbol{D}}_{{j_m}, k}}{\rm{cos}}{\zeta ^{(m)}} + {{\boldsymbol{D}}_{{j_{m + 2}}, k}}{\varphi ^{(m)}}{\rm{sin}}{\zeta ^{(m)}} + \\ \;{{\boldsymbol{D}}_{{j_{m + 1}}, k}}{\rm{sin}}{\zeta ^{(m)}} + {{\boldsymbol{D}}_{{j_{m + 3}}, k}}{\varphi ^{(m)}}{\rm{cos}}{\zeta ^{(m)}}) \end{array} $ | (4) |
式中:φ(m)是BPM与Kicker的夹角;ζ(m)是反馈信号所需的相移;G(m)是反馈所需的增益;矩阵D可参见文献[5]。
2.3 选择滤波器法选择FIR滤波器法的核心思想,是对一个与储存环的工作点相同频率正弦信号进行抽样作为冲击响应[8],FIR滤波器的系数:
| $ {a_k} = \sin (2{\rm{ \mathsf{ π} }}\upsilon (n-1)-\phi ) $ | (5) |
式中:1≤n<N,N是FIR滤波器的阶数;υ是储存环工作点;ϕ是可调相位。
3 反馈系统FIR滤波器设计方法分析 3.1 FIR滤波器的设计要求反馈系统的FIR滤波器主要功能是滤波。校正信号会受到来自信号中的直流分量和与反馈无关的振荡信号的干扰。直流分量会使放大器饱和[9],而且会干扰有效反馈信号,因而应优先考虑滤除直流分量。与该反馈无关的振荡信号会干扰有效的校正信号,故而应该抑制与该反馈无关的振荡信号。如果BPM和Kicker放置在同一位置,FIR滤波器要对检出信号移相90°。
很多同步辐射光源并没有使用纵向反馈系统,对撞机往往需要纵向反馈系统,但是为了方便后续研究,研究滤波器在纵向反馈中信号处理的使用是必要的。在纵向和横向反馈系统中,分别采用选择滤波器法和最小二乘法设计FIR滤波器,通过FIR滤波器的幅频响应和相频响应,分析滤波器的性能,选择最佳设计方法。以北京正负电子对撞机二期(BEPC-Ⅱ)的反馈系统为例,纵向工作点为0.037,横向垂直工作点为0.43,为简单起见,暂不考虑横向水平工作点。
3.2 纵向反馈中FIR滤波器的设计及分析在BEPC-Ⅱ纵向反馈系统中,采用选择滤波器法设计20阶FIR滤波器的幅频响应及相频响应如图 4所示。由图 4可知,FIR滤波器在纵向工作点的相位为-90°,纵向工作点处与0点处的信噪比为87.4dB,纵向工作点处与横向垂直工作点处的信噪比为19.6 dB。数据表明:该滤波器不仅可以实现信号的90°相移,也可以滤除直流分量,还在一定程度上抑制与该反馈无关的横向振荡信号,符合设计要求。

|
图 4 20阶FIR滤波器的幅频响应及相频响应 Figure 4 Amplitude-frequency response and phase-frequency response of 20-tap FIR filter |
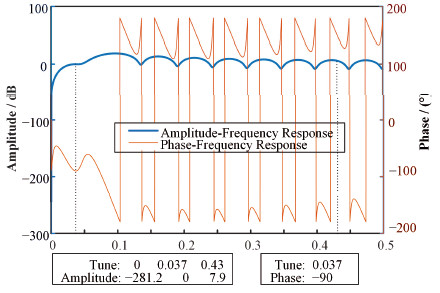
在BEPC-Ⅱ纵向反馈系统中,采用最小二乘法设计20阶FIR滤波器,相应的幅频响应及相频响应如图 5所示。由图 5可知,20阶FIR滤波器在纵向工作点处与横向垂直工作点处的信噪比是-7.9dB,所以,该滤波器不能有效抑制与该反馈无关的横向振荡信号。
|
图 5 20阶FIR滤波器的幅频响应及相频响应 Figure 5 Amplitude-frequency response and phase-frequency response of 20-tap FIR filter |
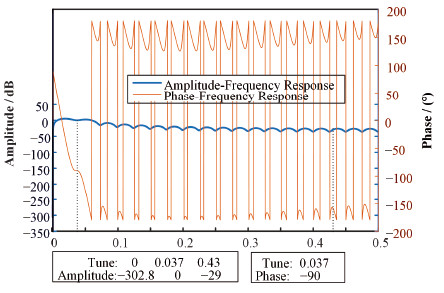
采用最小二乘法,增加FIR滤波器的阶数,设计40阶FIR滤波器,相应的幅频响应及相频响应如图 6所示。40阶FIR滤波器在纵向工作点的相位为-90°,纵向工作点处与0点处的信噪比为302.8dB,纵向工作点处与横向垂直工作点处的信噪比为29 dB,数据表明该滤波器符合设计要求。
|
图 6 40阶FIR滤波器的幅频响应及相频响应 Figure 6 Amplitude-frequency response and phase-frequency response of 40-tap FIR filter |
由上可见,在纵向反馈系统中,采用最小二乘法设计,可通过增加FIR滤波器阶数的方法,获得好的反馈信号。但是,随着滤波器阶数的增加,会占用更多的逻辑资源,增加设计复杂度。采用选择滤波器法设计FIR滤波器,较低阶FIR滤波器就可以获得同样好的反馈校正信号,结构也相对简单。
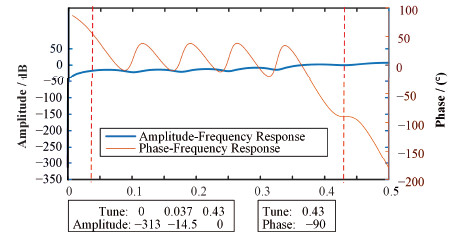
3.3 横向反馈中FIR滤波器的设计及分析在BEPC-Ⅱ横向反馈系统中,采用最小二乘法设计14阶FIR滤波器,其幅频响应和相频响应如图 7所示。从图 7可以看到,FIR滤波器在横向垂直工作点的相位为-90°,横向垂直工作点处与0点处的信噪比为313 dB,纵向工作点处与横向垂直工作点处的信噪比为14.5dB。数据表明:该滤波器可以实现信号的90°相移,滤除直流分量,还能抑制与该反馈无关的纵向振荡信号,符合设计的要求。
|
图 7 14阶FIR滤波器的幅频响应及相频响应 Figure 7 Amplitude-frequency response and phase-frequency response of 14-tap FIR filter designed by using the least square method |
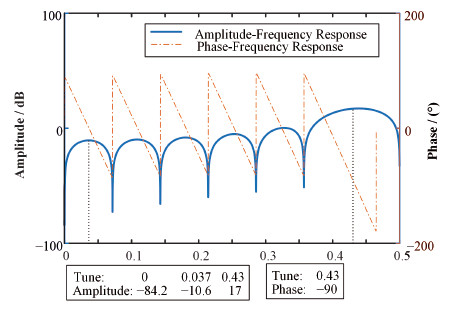
在BEPC-Ⅱ横向反馈系统中,采用选择滤波器法设计FIR滤波器,得到相应的幅频和相频响应如图 8所示。由图 8可知,14阶FIR滤波器在横向垂直工作点的相位为-90°,横向垂直工作点处与0点处的信噪比是101.2 dB,横向垂直工作点处与纵向工作点处的信噪比是27.6 dB,数据表明该滤波器也符合设计的要求,与最小二乘法设计的14阶滤波器相比,抑制与该反馈无关的纵向振荡信号效果更好。
|
图 8 14阶FIR滤波器的幅频响应及相频响应 Figure 8 Amplitude-frequency response and phase-frequency response of 14-tap FIR filter designed by using the selective filter method |
在反馈系统中,无论最小二乘法还是选择滤波法都能设计性能较好的FIR滤波器,由于最小二乘法涉及矩阵变换,算法复杂,为获得较好性能,需要较高的阶数,而选择滤波法设计FIR滤波器不需要太高阶数,算法简单,是最佳方案。
4 选择滤波器法设计FIR滤波器分析及优化 4.1 选择滤波器法设计FIR滤波器的优化在满足反馈系统FIR滤波器设计要求条件下,为了使选择滤波器法通用性更好,不再区分横向和纵向反馈系统。在工作点的相位可以线性调整,在相位调整过程中,围绕工作点具有带通响应,工作点处的增益基本恒定。原来的算法不能满足设计的要求。所以,需要对该滤波算法进行优化。
在原有选择滤波器法的基础上,令:
| $ \nu \cdot N{\rm{ }} = {P_0} $ | (5) |
式中:ν是工作点;N是滤波器阶数;P0是中间变量。
对P0近似求整,得整数P1:
| $ {P_1} \approx {P_0} $ | (6) |
当P1/N= 0时,p= 1;当P1/N= 0.5时,p= P1– 1;当P1/N≠ 0.5且P1/N≠ 0时,p= P1。
对于可调相位ϕ,令:
| $ \phi = \pi /m $ | (7) |
式中:m为相位调节系数,m值在一定范围内与相位之间有正向或反向的关系,只需小范围调节m值就可以轻松调节相位,进而得到相应的滤波系数。
优化后的表达式为:
| $ {a_k} = \sin (2\pi (n-1)\frac{p}{N}-\pi /m) $ | (8) |
式中:1≤n<N,N是FIR滤波器的阶数,N≥4;p是整数且大于0。
4.2 选择滤波器法设计FIR滤波器的滤波效果分析采用优化的选择滤波器法设计FIR滤波器,保证滤除直流分量以及能对检出信号移相90°的情况下,围绕工作点具有合适的带通,滤除无关振荡信号。所以,需要分析不同阶数FIR滤波器的幅频响应,研究滤波器阶数对围绕工作点的带通响应的影响,而带通响应一定程度上反映在围绕工作点的平滑曲线的水平跨度上,在此,研究围绕工作点的平滑曲线的水平跨度与滤波器阶数的关系。
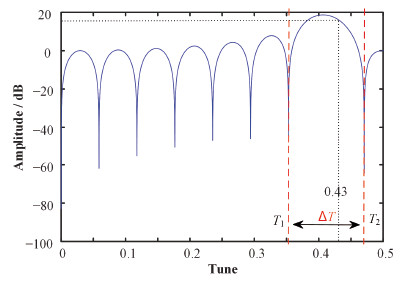
当工作点是0.43时,采用优化的选择滤波器法设计17阶FIR滤波器,其幅频响应如图 9所示,图 9中虚线1和虚线2之间“花瓣状”曲线即是围绕工作点0.43的平滑曲线,虚线1处工作点T1对应的幅值是该平滑曲线左边最小值,虚线2处工作点T2对应的幅值是该平滑曲线右边最小值,所以,该平滑曲线的水平跨度ΔT是从T1到T2,即ΔT = T2 - T1。
|
图 9 17阶FIR滤波器的幅频响应 Figure 9 Amplitude-frequency response of 17-tap FIR filter |
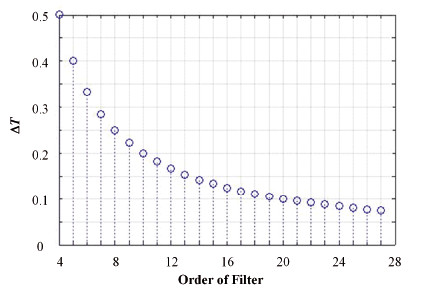
ΔT随滤波器阶数增加的变化情况如图 10所示,从图 10中数据可知,ΔT与滤波器阶数N有如下关系:
| $ \Delta T = 2/N $ | (9) |
|
图 10 ΔT随滤波器阶数增加的变化情况 Figure 10 ΔT changes with the increase of the filter order |
随着滤波器的阶数的增加,ΔT逐渐变小,反映了围绕工作点的通带变窄。因此,选择滤波器法设计FIR滤波器时,适当增加FIR滤波器的阶数,并观察此工作点与反馈无关振荡信号的信噪比,得到合适的窄带通,将与该反馈无关的振荡信号有效地滤除。
4.3 选择滤波器法设计FIR滤波器的可靠性分析加速器运行过程中,储存环的工作点会发生微小的漂移[10],这会引起FIR滤波器对信号移相变化,严重时,可导致反馈校正力的作用方向变化,使振荡程度加大,因而工作点漂移对FIR滤波器的影响不容忽视。采用优化的选择滤波器法设计FIR滤波器,通过FIR滤波器的相频响应,分析工作点漂移对不同阶数的FIR滤波器的相位影响,提高FIR滤波器工作的可靠性。
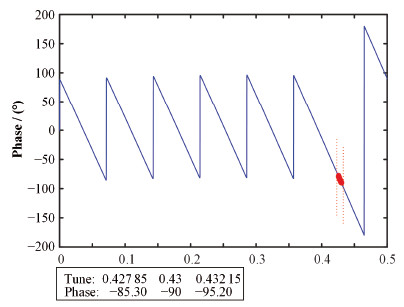
对于BEPCⅡ横向反馈系统,横向垂直工作点为0.43,选择滤波器法设计的14阶FIR滤波器的相频响应如图 11所示,横向垂直工作点在±0.5%之间漂移时,相位在- 84.30°~ - 95.20°之间变化,引起相位变化的峰峰值为10.90°。所以,横向垂直工作点漂移会引起FIR滤波器相位变化,相位变化的峰峰值的大小反映了影响的程度。
|
图 11 14阶FIR滤波器的相频响应 Figure 11 Phase-frequency response of 14-tap FIR filter |
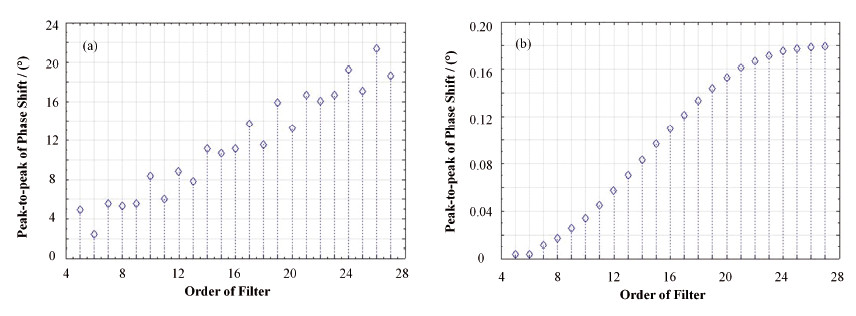
对不同阶数的FIR滤波器,横向垂直工作点漂移会引起FIR滤波器相位变化的峰峰值如图 12(a)所示,图中横坐标是滤波器的阶数,纵坐标是FIR滤波器相位变化的峰峰值。从图 12(a)可知,高阶的FIR滤波器从总体来看受到工作点漂移的影响较大。同样,对于BEPCⅡ纵向反馈系统,纵向工作点0.037在±0.5%之间漂移时,不同阶数的FIR滤波器相位变化的峰峰值如图 12(b)所示,随着阶数的增高,相位变化的峰峰值变大,即纵向工作点漂移影响变大。
|
图 12 横向垂直工作点(a)和纵向工作点(b)漂移引起不同阶数FIR滤波器相位变化的峰峰值 Figure 12 Peak-to-peak of the phase shift of different order of the FIR filter because of the vertical tune shift of transverse oscillation (a) and the tune shift of longitudinal oscillation (b) |
总之,采用选择滤波器法设计FIR滤波器时,适当减小滤波器的阶数,并在一定滤波器阶数范围内,选择工作可靠性更好的滤波器阶数。
5 结语在不同的反馈系统中,比较了采用最小二乘法和选择滤波器法设计FIR滤波器的差异,选择滤波器法设计FIR滤波器不仅性能好且设计简单,是较好的设计方法。通过对选择滤波器法的深入研究,提出选择滤波器法优化方法,设计FIR滤波器的过程中,根据实际需要选择合理的设计方法及参数,得到滤波器系数,当FIR滤波器满足滤波要求时,尽量采用较低阶的滤波器的设计。
| [1] |
Chen H J, Chen J, Gao B, et al. Bunch-by-bunch beam size measurement during injection at Shanghai Synchrotron Radiation Facility[J]. Nuclear Science and Techniques, 2018, 29: 79. DOI:10.1007/s41365-018-0420-2 |
| [2] |
Yang Y, Leng Y B, Yan Y B, et al. Development of the bunch-by-bunch beam position acquisition system based on BEEcube[J]. Nuclear Science and Techniques, 2016, 27: 47. DOI:10.1007/s41365-016-0035-4 |
| [3] |
Tobiyama M, Kikutani E. Development of a high-speed digital signal process system for bunch-by-bunch feedback systems[J]. Physical Review Special TopicsAccelerators and Beams, 2000, 3(1): 012801. DOI:10.1103/PhysRevSTAB.3.012801 |
| [4] |
栗武斌. HLS Ⅱ储存环数字逐束团反馈系统的研制[D].合肥: 中国科学技术大学, 2014. LI Wubin. Development of digital bunch-by-bunch feedback systems for the storage ring of HLS Ⅱ[D]. Hefei: University of Science and Technology of China, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10358-1014268805.htm |
| [5] |
Oxoby G, Serio M, Linscott I, et al. Bunch-by-bunch longitudinal feedback system for PEP-Ⅱ[R]. SCAN/9408216, 1994.
|
| [6] |
韩利峰, 袁任贤, 俞路阳, 等. FPGA横向反馈数字板在SSRF储存环的应用[J]. 核技术, 2008, 31(10): 736-739. HAN Lifeng, YUAN Renxian, YU Luyang, et al. The application of FPGA-based DSP module in the SSRF storage ring[J]. Nuclear Techniques, 2008, 31(10): 736-739. DOI:10.3321/j.issn:0253-3219.2008.10.004 |
| [7] |
Nakamura T. Single-loop multi-dimensional digital feedback by FIR filters[D]. Japan: Spring-8, 2009.
|
| [8] |
Hindi H, Eisen N, Fox J. Analysis of DSP-based longitudinal feedback system: trials at SPEAR and ALS[C]. Proceedings of the 1993 IEEE Particle Accelerator Conference, Washington, DC, 2002.
|
| [9] |
岳军会, 张磊, 马力, 等. BEPCⅡ横向束流反馈系统的梳状滤波器[J]. 强激光与粒子束, 2005, 17(12): 1917-1920. YUE Junhui, ZHANG Lei, MA Li, et al. Performance of a notch filter for BEPCⅡ[J]. High Power Laser and Particle Beams, 2005, 17(12): 1917-1920. |
| [10] |
邓庆勇, 曹建社, 岳军会, 等. BEPCⅡ储存环逐束团丢束监测系统及应用[J]. 强激光与粒子束, 2014, 26(10): 105101. DENG Qingyong, CAO Jianshe, YUE Junhui, et al. Bunch-by-bunch beam loss monitor system in BEPCⅡ storage ring[J]. High Power Laser and Particle Beams, 2014, 26(10): 105101. DOI:10.11884/HPLPB201426.105101 |


