X射线荧光光谱分析在生物医学、材料化学、探矿、有害物质检测等领域有着广泛的应用[1]。通过对X射线荧光光谱数据处理,实现样本中元素的定性分析和定量分析是X射线荧光分析的核心。在X射线荧光光谱分析数据处理[2]中,谱光滑可去除荧光光谱中由探测器的统计涨落和电子学噪声引起的噪声,直接影响定性分析和定量分析的效果。常用的谱光滑方法有移动平均法[3]、Savitzky-Golay多项式滤波器法(Savitzky-Golay Polynomial Filter Method, SGFM)[4]、傅里叶变换法[5]、小波阈值去噪法(Wavelet Threshold Denoising Method, WTDM)[6-7]等。移动平均法较为简单、快速,但容易引起光谱的失真,去噪效果较差。SGFM的去噪效果优于移动平均法,但需要选取合适的多项式次数和滤波器宽度。傅里叶变换法应用简单,效果较好,但阈值较难选取,这限制了傅里叶变换法的使用。WTDM光滑效果较佳,但过多的参数增加了WTDM的使用难度,如小波基函数[8]、分解层数、阈值函数、阈值等。
本研究通过交叉验证[9-10]确定傅里叶变换的最优阈值,使傅里叶变换法能自动执行。用仿真光谱测试基于交叉验证的最优阈值(Optimal Threshold based on Cross Validation, CVOT)和理论最优阈值(Theoretical Optimal threshold, TOT)之间的相对误差,并研究基于交叉验证的傅里叶变换法(Fourier Transform Method based on Cross Validation, CVFTM)和SGFM的去噪效果差异。
1 基本原理 1.1 傅里叶变换法傅里叶变换法是基于离散傅里叶变换进行的,离散傅里叶变换实现离散时间序列和离散频域序列间的变换。当含噪信号在时域不能分离噪声时,可考虑有用信号和噪声的频率差异,在频域实现去噪。
1) 将离散时间序列x(n)用离散傅里叶正变换转换到频域,得到离散频域序列Fx(m),变换式为[11]:
| $ {F_x}(m) = \sum\limits_{n = 0}^{N - 1} {x(n){{\rm{e}}^{ - j\frac{{2\pi }}{N}nm}}} \;\;\;(m = 0, 1, \ldots, N - 1) $ | (1) |
式中:N为时间序列的长度,频域序列和时间序列长度相同。
2) 设置阈值t,将频域序列中频率高于t的幅值置0,以滤除高频噪声,得到光滑后的频域序列
| $ {\hat F_x}\left( m \right) = \left\{ {\begin{array}{*{20}{c}} 0&{t < \frac{{{f_s} \times m}}{N} < {f_s} - t}\\ {{F_x}(m)}&{\rm{others}} \end{array}} \right. $ | (2) |
式中:fs为时间序列采样频率;(fs×m)/N为频域序列中第m个值对应频率。
3) 根据离散傅里叶反变换,将光滑后的频域序列
| $ \mathop x\limits^ \wedge (n) = \frac{1}{N}\sum\limits_{m = 0}^{N - 1} {{{\mathop F\limits^ \wedge }_x}(m){{\rm{e}}^{j\frac{{2\pi }}{N}nm}}} \;\;(n = 0, 1, \ldots, N - 1) $ | (3) |
为提高离散傅里叶变换的执行速度,在计算机上,使用快速傅里叶变换算法(Fast Fourier Transform, FFT)[11]编程实现离散傅里叶变换。为使用傅里叶变换去噪,时间序列的采样频率需满足奈奎斯特采样定理[11],即采样频率大于模拟信号最大频率的两倍。荧光光谱的自变量为道址,不具有时域特性,也没有采样频率的概念。当峰变化较为平缓,可以认为峰不包含高频信号,可以使用傅里叶变换。一般试验获得的峰均满足该条件,对于特别尖的峰,可以认为实验效果良好,不需要去噪。为将傅里叶变换法应用到荧光分析中,假定荧光光谱的采样频率fs为1。采样频率仅用于获得光谱序列和频率的对应关系,具体数值不影响傅里叶变换法的使用。
1.2 CVFTM为衡量信号光滑的效果,在式(4)中定义误差平方和函数M(t)为:
| $ M(t) = \sum\limits_{n = 0}^{N-1} {(\mathop x\limits^ \wedge (n)-} \dot x(n){)^2}\;\;(n = 0, 1, \ldots, N-1) $ | (4) |
式中:
|
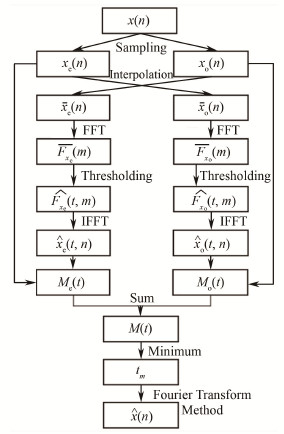
图 1 CVFTM的流程图 Figure 1 The flow chart of CVFTM |
1) 将原始光谱数据x(n)按照序号的奇偶性分为偶序号序列xe(n)和奇序号序列xo(n) (n=0, 1, …, N/2-1),其中:N为光谱数据x(n)的长度,一般取偶数。
2) 对奇序号序列xo(n)进行插值,得到偶序号序列的估计序列
| $ {\overline x _{\rm{e}}}(n) = \frac{{{x_{\rm{o}}}(n) + {x_{\rm{o}}}(n + 1)}}{2}\;(n = 0, 1, \ldots, N/2 - 1) $ | (5) |
规定xo(N/2)= xo(0)。
3) 对估计序列
4) 将xe(n)作为参考值,根据式(4)计算xe(n)和
| $ M(t) = \sum\limits_{n = 0}^{N/2 - 1} {{{\left( {{{\mathop x\limits^ \wedge }_{\rm{e}}}(t, n) - {x_{\rm{e}}}(n)} \right)}^2}} $ | (6) |
5) 对偶序号序列xe(n)应用步骤2)~6),得到估计的奇序号序列
| $ M(t) = {M_e}(t) + {M_o}(t) $ | (7) |
6) M(t)取最小值时的阈值即为最佳阈值tm,用其对x(n)做傅里叶变换去噪,得到光滑后的光滑信号
根据奈奎斯特采样定理,当x(n)的最大频率为fm时,xe(n)和xo(n)的采样频率应大于2×fm。因为xe(n)和xo(n)的采样频率是x(n)的采样频率的一半,所以x(n)的采样频率应大于4×fm。当假定x(n)的采样频率fs=1时,xe(n)和xo(n)的最大频率为0.25。因此,阈值t的取值范围为0~0.25,以间隔0.001获得阈值序列。对于不同的应用场合,可以适当改变阈值间隔。加大阈值间隔可以增加最优阈值精度,但也会增大算法运行时间,适应于精度要求高的场合。
2 实验 2.1 用仿真光谱测试CVOT的准确性在X射线荧光分析中,光谱的特征峰可以看作由高斯函数构成[2],在此基础上添加高斯本底,得到仿真光谱Sdata为:
| $ \begin{array}{l} {S_{\rm{data}}} = 10 \times {{\rm{e}}^{-\frac{{{{(i-200)}^2}}}{{15}}}} + 10 \times {{\rm{e}}^{-\frac{{{{(i - 475)}^2}}}{{90}}}} + 10 \times {{\rm{e}}^{ - \frac{{{{(i - 500)}^2}}}{{90}}}} + \\ {\begin{array}{*{20}{c}} {}&{} \end{array}^{}}{^{}_{}}10 \times {{\rm{e}}^{ - \frac{{{{(i - 540)}^2}}}{{200}}}} + 10 \times {{\rm{e}}^{ - \frac{{{{(i - 568)}^2}}}{{60}}}} + 10 \times {{\rm{e}}^{ - \frac{{{{(i - 790)}^2}}}{{120}}}} + \\ {\begin{array}{*{20}{c}} {}&{} \end{array}^{}}{^{}_{}}10 \times {{\rm{e}}^{ - \frac{{{{(i - 900)}^2}}}{{120}}}} + 10 \times {{\rm{e}}^{ - \frac{{{{(i - 600)}^2}}}{{180 000}}}} \end{array} $ | (8) |
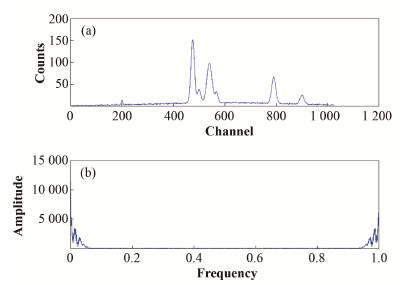
式中:i为道址(1~1024)。向仿真光谱添加高斯白噪声,得到信噪比为30 dB的含噪仿真光谱,如图 2(a)所示。图 2(b)为含噪仿真光谱的频谱图,采样频率为1。由图 2(b)得,有用信号的最大频率小于采样频率的1/4,可以使用CVFTM。
|
图 2 含噪仿真光谱的时域图(a)和频谱图(b) Figure 2 The time graph (a) and the frequency graph (b) of the noise simulation spectrum |
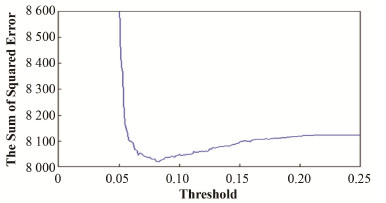
对图 2(a)中的仿真光谱应用CVFTM,根据式(7)得到误差平方和函数,如图 3所示。由误差平方和函数得到CVOT为0.083,此时误差平方和最小。用CVOT进行傅里叶变换去噪,得到光滑后仿真光谱的信噪比为36.29。
|
图 3 CVOT的误差平方和函数曲线 Figure 3 The sum of square error curve of CVOT |
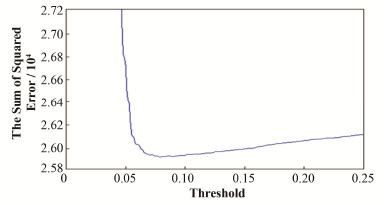
用傅里叶变换对图 2(a)中的仿真光谱做光滑处理,根据式(4)计算光滑后仿真光谱的误差平方和,如图 4所示。当阈值为0.080时,误差平方和最小,将其作为TOT。计算TOT对应的光滑后仿真光谱,其信噪比为36.51。比较CVOT和TOT可得,两个阈值相接近,去噪效果相同。
|
图 4 TOT的误差平方和函数曲线 Figure 4 The sum of square error curve of TOT |
向式(8)生成的仿真光谱添加不同大小的噪声,获得不同信噪比的含噪仿真光谱。对含噪仿真光谱,分别计算TOT和CVOT,由如下公式计算两个阈值的相对误差:
| $ \delta = |{t_{\rm{c}}} - {t_{\rm{r}}}|/{t_{\rm{r}}} $ | (9) |
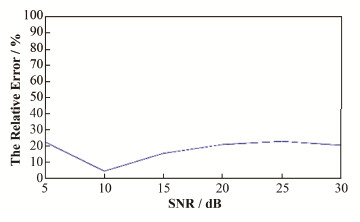
式中:δ为相对误差;tc为CVOT;tr为TOT。不同信噪比的含噪仿真光谱,由式(9)获得相对误差函数示于图 5。试验表明,相对误差的最大值小于30%。因此,CVOT在不同信噪比(Signal-to-Noise Ratio, SNR)下均是合适的。
|
图 5 不同信噪比下TOT和CVOT的相对误差 Figure 5 The relative error of TOT and CVOT under different SNR |
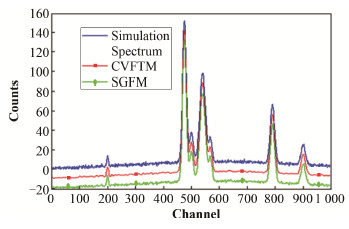
为测试CVFTM的光滑效果,将SGFM作为参照,分别对图 2(a)中的含噪仿真光谱做光滑处理。SGFM的滤波器宽度为5,多项式次数为3,执行次数为1。图 6为CVFTM和SGFM的光滑效果图,将两种方法光滑后的光谱在坐标轴上分别下移10和20。由图 6得,CVFTM去噪后的光谱更加平滑,效果更好。
|
图 6 CVFTM和SGFM的光滑效果图 Figure 6 The smoothed simulation spectra of CVFTM and SGFM |
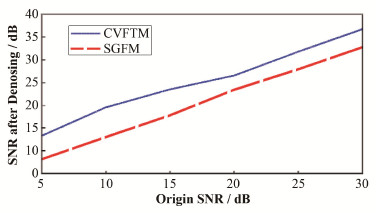
为比较不同信噪比下,CVFTM和SGFM的去噪效果,向式(8)生成的仿真光谱添加不同大小的噪声,获得不同信噪比的含噪仿真光谱。用CVFTM和SGFM分别对不同信噪比的含噪仿真光谱做光滑,计算光滑后光谱的信噪比,结果如图 7所示。由图 7得,在不同信噪比下,CVFTM的去噪效果远优于SGFM。
|
图 7 不同信噪比下CVFTM和SGFM光滑后光谱的信噪比 Figure 7 SNR of the smoothed simulation spectrum of CVFTM and SGFM at different SNR |
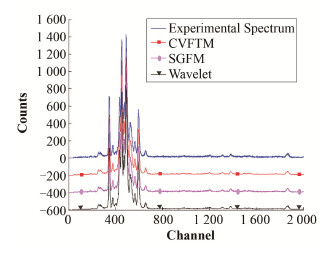
通过能量色散型X射线荧光光谱仪获得实际光谱,分别将CVFTM、SGFM和小波阈值去噪法应用到实际光谱,得到如图 8所示的效果图。对比原始光谱曲线和CVFTM处理后的光谱曲线,CVFTM曲线更加平滑,未引起特征峰的失真,去噪效果良好。在CVFTM和SGFM的对比试验中,SGFM的滤波器宽度为5,多项式次数为3,执行次数为1,CVFTM光滑效果优于SGFM。在CVFTM和小波阈值去噪法的对比试验中,CVFTM能达到小波阈值去噪法的光滑效果,但CVFTM使用更加简洁。
|
图 8 三种方法应用到实际光谱的效果图 Figure 8 The denoising results of three denosing methods for experimental spectrum |
本文提出了利用交叉验证傅里叶变换法进行光谱光滑处理的新方法,由交叉验证自动确定傅里叶去噪的最佳阈值。将该方法应用于仿真光谱和实际光谱。结果表明:CVOT和TOT之间的相对误差小于30%,该方法可以准确地去除噪声。和SGFM相比,CVFTM的光滑效果更优。和小波阈值去噪法相比,CVFTM在使用时不需人为确定参数。因此,在X射线荧光光谱光滑处理中,CVFTM是一种准确、便捷的方法。该方法对使用人员要求不高,在要求光谱仪自动给出分析结果、便携式应用等场合具有很大的应用前景。
| [1] |
杨明太, 唐慧. 能量色散X射线荧光光谱仪现状及其发展趋势[J]. 核电子学与探测技术, 2011, 31(12): 1307-1311. YANG Mingtai, TANG Hui. The actualities and trend of energy dispersive X-ray fluorescence spectrometry[J]. Nuclear Electronics & Detection Technology, 2011, 31(12): 1307-1311. DOI:10.3969/j.issn.0258-0934.2011.12.001 |
| [2] |
赵奉奎.能量色散型X射线荧光光谱仪关键技术研究[D].南京: 东南大学, 2015. ZHAO Fengkui. Research on key technologies of energy dispersive X-ray fluorescence spectrometer[D]. Nanjing: Southeast University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10286-1016050274.htm |
| [3] |
Azami H, Mohammadi K, Bozorgtabar B. An improved signal segmentation using moving average and Savitzky-Golay filter[J]. Journal of Signal and Information Processing, 2012, 03(01): 39-44. DOI:10.4236/jsip.2012.31006 |
| [4] |
Savitzky A, Golay M J E. Smoothing and differentiation of data by simplified least squares procedures[J]. Analytical Chemistry, 1964, 36(8): 1627-1639. DOI:10.1021/ac60214a047 |
| [5] |
Zhang Q, Ge L, Gu Y, et al. Background estimation based on Fourier transform in the energy-dispersive X-ray fluorescence analysis[J]. X-ray Spectrometry, 2012, 41(2): 75-79. DOI:10.1002/xrs.2360 |
| [6] |
Donoho D L, Johnstone I M. Adapting to unknown smoothness via wavelet shrinkage[J]. Journal of the American Statistical Association, 1995, 90(432): 1200-1224. DOI:10.1080/01621459.1995.10476626 |
| [7] |
Donoho D L, Johnstone I M. Ideal spatial adaptation by wavelet shrinkage[J]. Biometrika, 1994, 81(3): 425-455. DOI:10.2307/2337118 |
| [8] |
Cunha C F F C, Carvalho A T, Petraglia M R, et al. A new wavelet selection method for partial discharge denoising[J]. Electric Power Systems Research, 2015, 125: 184-195. DOI:10.1016/j.epsr.2015.04.005 |
| [9] |
Pasti L, Walczak B, Massart D L, et al. Optimization of signal denoising in discrete wavelet transform[J]. Chemometrics and Intelligent Laboratory Systems, 1999, 48(1): 21-34. DOI:10.1016/S0169-7439(99)00002-7 |
| [10] |
Nason G P. Wavelet shrinkage using cross-validation[J]. Journal of the Royal Statistical Society, 1996, 58(2): 463-479. |
| [11] |
MitraS K. 数字信号处理-基于计算机的方法[M]. 2版. 北京: 清华大学出版社, 2001. Mitra S K. Digital signal processing:a computer-based approach[M]. 2nd ed. Beijing: Tsinghua University Press, 2001. |


