反应堆、铀矿开采、乏燃料后处理等核设施在运行期间,将不可避免产生裂变产物、衰变子体及活化产物[1]。其中裂变及衰变输运过程中产生的可能以固体粒子形态存在[2]的有90Sr、83Br、137Cs、212-218Po、212Pb、212Bi等,具有很强附着力及α或β放射性,能与空气微粒形成结合态;此外,以气体形态存在如131I、41Ar、85Kr、133Xe等也能与空气微粒相结合,由此产生放射性气溶胶。放射性气溶胶具有多形、多孔和吸附性[3],能较长时间悬浮于空气中。工作人员吸入后可引起呼吸系统、免疫功能、内分泌系统损伤,增加心脏疾病、慢性阻塞性肺病、肺肿瘤发病率等一系列健康危害[4]。因此,必须对工作环境中的放射性气溶胶含量进行在线监测。
放射性气溶胶粒子在实际的测量过程中将发生一定的损失,主要是因为气溶胶颗粒在输运过程中发生沉积作用。如何提高放射性气溶胶颗粒测量的有效性,需对相关监测仪的气溶胶颗粒运动及穿透率进行模拟分析,并结合实验,给出较好的测量途径及指导意见[5-6]。关于气溶胶监测仪内相关的颗粒输运沉积模拟国内开展较少,主要集中在如圆管、弯管、立方体管内及普通室内等[7-9]。如采用fluent-滑移通量模型进行室内220Rn及其子体输运的计算流体力学(Computational Fluid Dynamics, CFD)模拟等[10];采用fluent-DPM模型进行文丘里管气固模拟[11]等。结果表明:Fluent对于气固两相流模拟具有一定的适用性。
本文使用流体力学仿真软件Fluent,对计算模型离散相模型(Discrete Phase Model, DPM)进行文献验证,证明该模型的可行性。然后以一种放射性气体气溶胶连续监测仪的测量腔室[5]作为研究对象,对空气动力学直径为1~5 μm的气溶胶颗粒沉积特性进行模拟研究,为放射性气溶胶连续监测仪的探测效率提供参考。
1 研究方法CFD是目前研究气溶胶输运沉积的主要手段。Fluent作为CFD软件中典型的一种,针对气固两(多)相流输运研究方法有三种[11-15]:1)拉格朗日法,即DPM模型;2)欧拉法;3)滑移模型。其中,DPM模型可以对不同粒径大小的颗粒在流场中进行跟踪模拟,对复杂几何流场适应性较强;滑移模型对于使用的滑移系数依赖性较高;欧拉法计算过程更为复杂,对计算机要求较高。
1.1 DPM模型DPM模型是Fluent开发的专门的离散相模型,由Crowe[16]和Smoot[17]等提出,是研究气固两相流离散相最有力的工具。具体解法分为两步:1)对连续相流体,在Euler坐标系下,求解Navier-Stokes方程,当计算结果收敛到适当程度(如残差设为0.001),将颗粒注入流场;2)对离散相流体,在拉格朗日坐标系下,以单个颗粒为对象,求解颗粒轨道方程,当计算再次收敛时,得到计算结果,对其进行统计处理,得出颗粒浓度、轨迹及其它统计量。Fluent中通过对颗粒作用力微分方程进行积分,来求解离散相颗粒轨迹。根据牛顿定律,颗粒的作用力平衡方程在笛卡尔坐标系下的形式(以x方向为例),如式(1)所示:
| $ m(\frac{{{\rm{d}}{u_{\rm{p}}}}}{{{\rm{d}}t}}) = {F_{\rm{d}}} + m{g_x}\frac{{{\rho _{\rm{p}}}-\rho }}{{{\rho _{\rm{p}}}}} + {F_x} $ | (1) |
式中:m为单颗粒质量,kg;up为颗粒速度,m·s-1;Fd为颗粒所受曳力;ρp为颗粒密度,kg·m-3;ρ为空气密度,kg·m-3;Fx为x方向上其它力。
通过对式(1)进行积分,可以得到颗粒轨道上每个位置的颗粒速度,对其运动方程积分,可以得到离散相颗粒的轨迹等。使用DPM模型需忽略颗粒间的相互作用,因此要求颗粒相的体积分数低于或等于10%。
1.2 颗粒受力离散相固体颗粒在稀疏气固两相流场中运动时,颗粒之间、颗粒与周围气体之间将不断发生相互作用,可分为以下几类:1)流体-颗粒相对运动无关的力,如惯性力、重力、布朗扩散力、压差力、热泳力、磁泳力、电泳力等;2)依赖于流体-颗粒间相对运动的力,如曳力、附加质量力、Basset力、Magnus升力和Saffman升力等。不同的力在颗粒运动中起到的作用不同,因而处理的方式不同。式(2)~(5)分别对颗粒所受的曳力、Saffman升力、虚假质量力及压力梯度力进行了介绍。
颗粒在流体中受到的曳力是颗粒与流体间相互作用的最基本形式。如式(2)所示:
| $ {F_{\rm{d}}} = \frac{\pi }{2}r_{\rm{p}}^{^2}{C_{\rm{D}}}\rho \left| {\mu-{\mu _{\rm{p}}}} \right|(\mu-{\mu _{\rm{p}}}) $ | (2) |
式中:μ为气相流体速度,m·s-1;ρ为气体密度,kg·m-3;rp为颗粒半径,μm;CD为曳力系数;μp为颗粒速度,m·s-1。
Saffman升力是由于颗粒在具有速度梯度的流场中运动,颗粒上下侧流体的速度差对颗粒产生的升力,如式(3)所示:
| $ {F_{\rm{Saf}}} = 1.61 \times {(\mu \rho )^{1/2}} \times d{{\rm{p}}^2} \times (\mu-{\mu _{\rm{p}}}) \times {\left| {\frac{{{\rm{d}}u}}{{{\rm{d}}y}}} \right|^{1/2}} $ | (3) |
式中:μ为空气的动力粘度;dp为颗粒粒径。
由表观质量效应产生虚假质量力,如式(4)所示:
| $ {F_{\rm{\nu m}}} = \frac{\rho }{2}{V_{\rm{p}}}(\frac{{{\rm{d}}u}}{{{\rm{d}}t}}-\frac{{{\rm{d}}{u_{\rm{p}}}}}{{{\rm{d}}t}}) $ | (4) |
式中:Vp为颗粒体积,m3。
颗粒在有压力梯度的气相流场中运动,受到由于压力梯度对颗粒引起的作用力,即压力梯度力,如式(5)所示:
| $ {F_{\rm{p}}} =-\frac{4}{3}\pi \times r_{\rm{p}}^3 \times \frac{{\partial p}}{{\partial x}} $ | (5) |
这个力实际就是通常所说的浮力,其中:rp为颗粒半径,μm;p为压力,Pa。
颗粒所受的曳力、Saffman力、虚假质量力及压力梯度力等,在DPM相应面板里可以进行勾选设置及修改。其他相关的受力在§1.3进行简单介绍。
1.3 颗粒受力大小与取舍气固两相流中离散相颗粒受力种类繁多,结合具体气体流场特点,对颗粒所受各种力进行有效取舍。岑可法[15]在《工程气固多相流动的理论及计算》中,对颗粒在周期性脉动平直气流中运动的颗粒作用力进行了比较。一般来说,颗粒曳力最大最明显,一定条件下,其他形式作用力可忽略,但曳力必须考虑。颗粒所受重力约比曳力小1~2个数量级,随颗粒尺寸增大,重力与曳力相差比例越小;Saffman升力及虚假质量力比曳力小大3~4个数量级。
在DPM模型中,考虑曳力、重力、虚假质量力、Saffman力、Magnus升力等情况。但是不考虑Basset力。
Basset力只在加速初期产生,针对本文研究稳态工况,颗粒比气体密度大三个量级,该力忽略不计。对于Magnus力,除非是颗粒旋转很强,或转动的大颗粒,否则可以忽略不计。此外,热泳力、电泳力、光泳力等通常情况下可以忽略不计。
1.4 壁面碰撞气固两相流中气溶胶颗粒在扩散及输运过程中将与接触的壁面发生碰撞,颗粒的物理性质及运动状态、速度、入射角度等都将对颗粒与壁面的碰撞沉积产生影响,目前没有适用于颗粒与壁面碰撞规律的通用模型。在DPM模型中,通常采用反射(reflect)、捕集(trap)和逃逸(escape)这三种边界条件进行处理。
2 方法验证针对不同管道模型下的空气动力学直径为1~2mm的气溶胶颗粒沉积进行模拟研究,通过与文献比较[18-19],以确定本文采用计算方法的准确性。
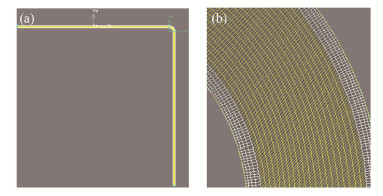
2.1 建模及网格划分模型1[18]分为平直段、弯管段和垂直段。平直段尺寸为3000 mm×50 mm(长×直径)。弯管段为外圆半径100 mm、内圆半径50 mm的1/4圆环。垂直段尺寸为2000 mm ×50 mm(长×直径)。采用四边形网格进行划分。管壁采用局部加密法,分为4层。文献中采用fluent-拉格朗日(即DPM)模型进行模拟计算,假定气体速度为2 m·s-1。在此,建立模型如图 1所示。
|
图 1 管道模型1 (a)示意图,(b)放大图 Figure 1 Pipe model 1 (a) Schematic diagram, (b) Enlargement diagram |
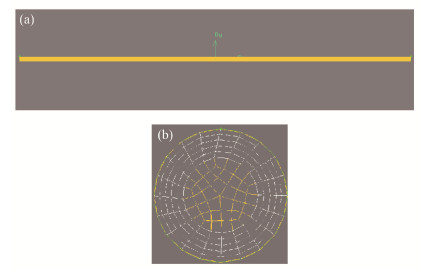
模型2[19]中参数大致为:气溶胶取样系统管长为2.5 m,管内径为2.5 cm,文献中采用实验方法进行测量,取气流速度35 L·min-1(即2 m·s-1)。建立模型,对管道近壁面处进行加密处理,细分为5层,比例为1.2。管道建模图及放大图见图 2所示。
|
图 2 管道模型2 (a)示意图,(b)放大图 Figure 2 Pipe model 2 (a) Schematic diagram, (b) Enlargement diagram |
在DPM的设置选项-“Discrete Phase Model”面板中,通过定义颗粒的初始位置、速度、粒径、温度等参数,再加上颗粒的物理属性,以此作为计算颗粒轨迹和颗粒热、质传递的初始化条件。对上述模型1-弯管及模型2-横管的气相场均采用湍流模式,颗粒相采用DPM模型。
在此假设颗粒为惰性固体颗粒,即非液滴形态,不考虑蒸发、流失等情况(该两种现象所占份额较小,约0.6%),主要考虑的受力有:曳力、重力、Saffman升力、虚假质量力等,出入口设为escape模式,壁面采用trap捕集模式。计算结果如表 1所示。
| 表 1 模拟结果比较 Table 1 Comparison of simulation results |
由表 1可见,采用Fluent中DPM模型对于粒径为1~2 μm的气溶胶颗粒输运沉积行为具有较高的准确性:与模型1(弯管)中采用的Fluent气固两相流模型及模型2(横管)中的实验测量结果的穿透率均具有98%以上的一致性。
3 放射性气溶胶测量腔室模拟放射性气溶胶连续监测仪[5]主要由采样测量系统(腔室)、探测器、滤膜(滤纸)、数据信号采集与处理、上位机及软件等组成。总体尺寸为330mm×229 mm×213.5 mm。其中,采样测量腔室分为两部分:外部球形气体收集腔以及锥形分流体。外部气体收集测量腔采用球形设计,以保证气流方向在腔室内部能够平滑变化,以减小粒子在腔室中的损失;赤道位置为上下两半球分界线,此位置设置凹槽,以便在采样时放置O形密封圈进行密封;内表面精抛光,尽量减小气溶胶粒子在其表面的粘附;下部开孔小于滤膜托盘尺寸,以防止气体泄漏致下部滤膜腔室。
监测仪内的抽气流量范围为20~70 L·min-1,具体工作过程为:采样测量系统(腔室)完成对工作场所空气的采样,气溶胶颗粒流过腔室并经腔室出口流出,直接进入滤膜上以进行放射性气溶胶颗粒收集,送给能谱探测器进行辐射检测;过滤后的气体输送至气体腔室,进行相关测量。
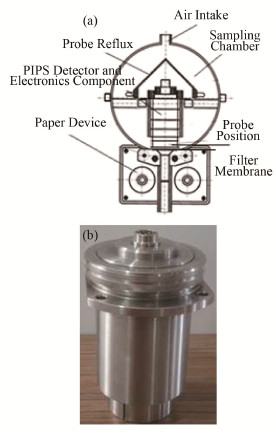
放射性气溶胶连续监测仪如图 3所示。
|
图 3 放射性气体气溶胶连续监测仪 (a)设计图,(b)实体图 Figure 3 Radioactive gas aerosol continuous monitor (a) Designer model, (b) Entity model |
以放射性气溶胶连续监测仪的测量腔室作为研究对象,使用gambit软件建立物理模型,并采用四面体进行结构化网格划分。本次在入口流速、颗粒大小流量等均不变的情况下,进行三种不同尺寸网格划分,对测量腔室内的倒流冒等内部壁面进行适当网格加密。网格栅元数分别为:26964、106954、425100个。节点数、最小体积尺寸、最小面积等均大于0,不存在负网格。其中网格划分方式二的建模如图 4所示。

|
图 4 放射性气体气溶胶监测仪测量腔室 (a)示意图,(b)放大图 Figure 4 Measuring chamber of radioactive gas aerosol monitoring system (a) Schematic diagram, (b) Enlargement diagram |
使用Fluent软件进行流体仿真模拟,设定合理的算法及边界条件。采用气流出口流速为35L·min-1,由此得出稳态时,入口流速为1.855m·s-1,对测量腔室进行收敛性计算。模拟气相控制方程采用k-ε模型,三维单精度求解器,残差设为1×10-5,离散格式为一阶迎风格式,管道入口采用速度入口模式,出口为自由流模式。对三种网格划分方式进行模拟,在计算达到5000步以上,收敛系数低于1×10-5,达到收敛目标。
3.3 流体流场计算由于网格划分方式二的网格数目适中,因此本次采用此网格模型进行流体流场计算。本次采用DPM模型,主要考虑重力、曳力、Saffman力、压力梯度力及虚假质量力等。出入口采用escape模式,与颗粒相接触的壁面采用trap捕集模式。计算结果如图 5所示。

|
图 5 放射性气溶胶测量腔室内流场计算 (a)流体流速分布,(b)颗粒浓度分布 Figure 5 Flow field calculations of radiative aerosol (a) Velocity distribution, (b) Particles distribution |
由图 5(a)可见,流体在监测仪测量腔室内发生射流及弥散,存在一定的气流漩涡,气流在沿流场方向速度相对较大,如靠近探头倒流帽、监测仪下半部及靠近出口等位置,其余区域气流速度较小。由图 5(b)可见,气溶胶颗粒在沿流场方向浓度较高,其中在探头倒流帽的下部分布最高。根据颗粒注入动态显示,大量的气溶胶颗粒(主要受曳力、重力及流场作用)沿着主流道进行射流。其中,少部分气溶胶颗粒将直接沉积于监测仪测量腔室的下半部壁面上。其余气溶胶颗粒在碰到下半部壁面后,发生反弹、涡流及流出:1)其中一部分气溶胶颗粒向下反弹流动,随着涡流沉积于测量腔室的内部取样管上,或由腔室出口流出,到达测量滤膜上供实际探测;2)还有少量气溶胶颗粒向上反弹,进入测量腔室的上半部分区域。与此同时,还有部分气溶胶颗粒在进入腔室之后,进行弥散流动,最终沉积于壁面或由出口流出达到测量滤膜。
3.4 穿透率计算根据文献[14],DPM模型主要用来模拟单个大颗粒的运动,一般是1 mm以上颗粒,即超微米颗粒,不能很好地模拟超细颗粒的运动,因此在此对粒径为1 mm、2 mm、5 mm的气溶胶颗粒进行输运沉积模拟,分别取入口流速为1.855 m·s-1、3.183m·s-1,计算结果如表 2所示。
| 表 2 放射性气体气溶胶连续监测系统穿透率 Table 2 Penetration rate of particles in gas aerosol continuous monitoring system |
由表 2可以得出以下结论:1)在流速不变的情况下,随着气溶胶颗粒尺寸的增加,相应的穿透率有所减小。此时的气溶胶主要受重力影响,布朗扩散及剪切应力等作用较小,颗粒越重,气溶胶颗粒沉积越多,穿透率越低,其中当粒径为5 μm时,穿透率低至30%左右;2)在气溶胶颗粒粒径不变的情况下,随着颗粒流速的增加,颗粒穿透率在一定程度上有所增加,此时流场更趋于紊流,颗粒穿过率越高。因此,适当增加颗粒流速,减小颗粒尺寸,有利于增加测量腔室内气溶胶颗粒的透过率,即达到测量滤膜可供探测的效率更高。
4 结语本文对计算流体力学fluent-DPM模型进行了介绍,经与相关文献内气溶胶颗粒输运沉积进行了模拟比较。结果表明:DPM模型对于气溶胶颗粒粒径为1~2 μm的输运沉积模拟,与参考文献模拟以及实验测量结果达到98%以上的一致性,因此验证了DPM模型对于气固两相流模拟的准确性。
采用DPM模型对放射性气溶胶监测仪测量腔室内的颗粒沉积情况进行了研究。得出以下结论:1)气溶胶颗粒流动过程中受到探头密封盖(倒流冒)、下半球壳体等的冲击,产生气流漩涡及进行沉积;2)气溶胶颗粒穿透率受气溶胶尺寸、流速、流动空间的形状等影响。一定范围内,流速增加、颗粒尺寸减小,颗粒穿透率则越大,即颗粒透过测量腔室到达测量滤膜的效率越高;3)对于入口流速为1.85~3.18 m·s-1、粒径为1~2 μm的气溶胶颗粒,在测量腔室内的透过率在80%~60%,对于粒径为5μm的气溶胶颗粒透过率低至30%左右。
由于气溶胶颗粒输运沉积过程较为复杂,与颗粒本身(尺寸、流速、比例)、流动区域、壁面粗糙度、颗粒悬浮与再悬浮等有关,目前国内外没有统一的研究结果及经验公式。相关参数的选择及设置是对实际流场的简化。本文为放射性气溶胶监测仪的探测效率提供了分析及参考。在下一步的工作中将结合实验进行各项因素分析。
| [1] |
彭红花, 严睿, 朱贵凤, 等. MCNP5在固态燃料熔盐堆功率分布计算的应用[J]. 强激光与粒子束, 2018, 30(01): 144-149. PENG Honghua, YAN Rui, ZHU Guifeng, et al. Application of MCNP5 in power distribution calculations of solid fuel molten salt reactor[J]. High Power Laser and Particle Beams, 2018, 30(01): 144-149. DOI:10.11884/HPLPB201830.170230 |
| [2] |
陈祥磊, 王益元, 熊启发, 等. 核电站放射性气溶胶探测器入射粒子模拟分析[J]. 舰船科学技术, 2011, 33(8): 53-57. CHEN Xianglei, WANG Yiyuan, XIONG Qifa, et al. Simulation of radioactive aerosol monitoring of nuclear power plant[J]. Ship Science and Technology, 2011, 33(8): 53-57. DOI:10.3404/j.issn.1672-7649.2011.08.012 |
| [3] |
刘祥宝, 张金萍, 朱琳琳. 室内颗粒物分布运动的研究进展[J]. 建筑热能通风空调, 2009, 28(5): 39-44. LIU Xiangbao, ZHANG Jinping, ZHU Linlin. The study development of particle dispersion and motion in indoor environments[J]. Building Energy & Environment, 2009, 28(5): 39-44. DOI:10.3969/j.issn.1003-0344.2009.05.010 |
| [4] |
高红武. 室内空气中可吸入颗粒物的监测与研究[J]. 云南冶金, 2006, 35(3): 75-77. GAO Hongwu. Monitoring and studying the inhalable particulate matter in indoor air[J]. Yunnan Metallurgy, 2006, 35(3): 75-77. DOI:10.3969/j.issn.1006-0308.2006.03.020 |
| [5] |
蔡军, 陈明明, 徐杰, 等.放射性气体气溶胶连续监测仪的研制[C].辐射防护年会论集, 2017. CAI Jun, CHEN Mingming, XU Jie, et al. The development of radioactive aerosols and nobel gases continuous monitor[C]. Annual Conference on Radiation Protection, 2017. |
| [6] |
陈峰, 夏晓彬, 张志宏, 等. 放射性α气溶胶监测仪数据采集系统的设计[J]. 核技术, 2015, 38(6): 060401. CHEN Feng, XIA Xiaobin, ZHANG Zhihong, et al. Design of data acquisition system for radioactive α aerosols monitor[J]. Nuclear Techniques, 2015, 38(6): 060401. DOI:10.11889/j.0253-3219.2015.hjs.38.060401 |
| [7] |
Abhijit Guha. Transport and deposition of particles in turbulent and laminar flow[J]. Annual Review of Fluid Mechanics, 2008, 40: 311-341. DOI:10.1146/annurev.fluid.40.111406.102220 |
| [8] |
Mark R S, William W N. Particle deposition in ventilation ducts:connectors, bends and developing turbulent flow[J]. Aerosol Science and Technology, 2005, 39(2): 139-150. DOI:10.1080/027868290908795 |
| [9] |
刘洪涛.气固两相流中微细颗粒沉积与扩散特性的数值研究[D].重庆: 重庆大学, 2010. LIU Hongtao. Numerical simulation of micro-particle deposition and diffusion characteristics in gas-solid two-phase flow[D]. Chongqing: Chongqing University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10611-2010215514.htm |
| [10] |
宋想.室内220Rn及其子体输运的CFD模拟[D].衡阳: 南华大学, 2013. SONG Xiang. The CFD simulation of indoor thoron and it's progeny migrations[D]. Hengyang: University of South China, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10555-1013341050.htm |
| [11] |
李红文, 张涛. 文丘里管内气固两相流离散相仿真模型优化[J]. 合肥工业大学学报(自然科学版), 2014, 37(1): 42-47. LI Hongwen, ZHANG Tao. Optimization of DPM simulation model of gas-solid two-phase flow in venture tube[J]. Journal of Hefei University of Technology (Natural Science), 2014, 37(1): 42-47. DOI:10.3969/j.issn.1003-5060.2014.01.010 |
| [12] |
江帆, 黄鹏. FLUENT高级应用与实例分析[M]. 北京: 清华大学出版社, 2008: 7. JIANG Fan, HUANG Peng. FLUENT advanced application and example analysis[M]. Beijing: Tsinghua University Press, 2008: 7. |
| [13] |
王福军. 计算流体动力学分析-CFD软件原理及应用[M]. 北京: 清华大学出版社, 2004. WANG Fujun. Computational fluid dynamics analysis-the principle and application of CFD software[M]. Beijing: Tsinghua University Press, 2004. |
| [14] |
李孔清, 龚光彩, 汤广发, 等. 悬浮颗粒数值模拟模型改进研究及应用[J]. 建筑热能通风空调, 2006, 25: 86-90. LI Kongqing, GONG Guangcai, TANG Guangfa, et al. Improving model for simulation of indoor suspension particles and its application[J]. Builiding Energy & Environment, 2006, 25: 86-90. DOI:10.3969/j.issn.1003-0344.2006.02.020 |
| [15] |
岑可法, 樊建人. 工程气固多相流动的理论及计算[M]. 杭州: 浙江大学出版社, 1990. CEN Kefa, FAN Jianren. Theory and calculation of engineering gas solid multiphase flow[M]. Hangzhou: Zhejiang University Press, 1990. |
| [16] |
Crowe C T, Chung J N, Troutt T R. Particle mixing in free shear flows[J]. Progress in Energy and Combustion Science, 1988, 14: 171-194. DOI:10.1016/0360-1285(88)90008-1 |
| [17] |
Smoot L D, Smith P J. Coal combustion and gasification[M]. New York: Plenum Press, 1985. DOI:10.1007/978-1-4757-9721-3
|
| [18] |
李成果, 屈国普, 屈世骏, 等. 核电站一回路压力边界泄漏监测氟-18传输效率分析[J]. 核电子学与探测技术, 2012, 32(3): 316-320, 351. LI Chengguo, QU Guopu, QU Shijun, et al. 18F transit efficiency analysis for press boundary of the first loop leak monitoring in nuclear plant[J]. Nuclear Electronics & Detection Technology, 2012, 32(3): 316-320, 351. DOI:10.3969/j.issn.0258-0934.2012.03.017 |
| [19] |
李爱武, 张志龙, 傅翠明, 等.气溶胶取样管道中粒子损失的实验研究[A].全国放射性流出物和环境监测与评价研讨会论文汇编[C].北京: 中国核学会, 2003: 9. LI Aiwu, ZHANG Zhilong, FU Cuiming, et al. Experimental study on particle loss in aerosol sampling pipeline[A]. National symposium on radioactive effluent and environmental monitoring and evaluation[C]. Beijing: China Nuclear Society, 2003: 9. |


