2. 海洋国家实验室海洋矿产资源评价与探测技术功能实验室 青岛 266071;
3. 长庆油田分公司第六采气厂 西安 710000
2. Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266071, China;
3. Changqing Oil Field Branch Sixth Gas Production Plant, Xi'an 710000, China
在随钻测井中,井眼尺寸(井径)的变化影响着仪器测量精度,不仅是消除密度、中子孔隙度、自然γ测井等方法井眼影响的重要参数,同时还可以利用井径信息估算固井所需的水泥量、定位石油开采过程中裂缝带的位置、直观形象地反应井壁稳定性。传统电缆测井是在钻井完后利用机械推靠臂测量井径。而随钻测井是在钻井的钻进过程中测量地下信息,这与电缆测井的仪器结构、施工方式以及测量环境上存在很大的差别。Maeso等[1]提出了在随钻测井中利用超声回波时间差确定仪器与井壁的距离并计算井径尺寸的方法,但泥浆比重的增大会使超声波信号衰减严重,测量的可靠性就会下降,一般常规测量技术仅适用泥浆比重小于1.3g·cm-3的条件。另外,超声波井径仪在工作时探头和仪器壳体会产生余震以及超声波反射时电路的电流瞬间很强会使仪器测量产生盲区,目前超声波井径仪的测量范围基本上在3 cm以上[2-3]。而当间隙在超声井径的测量盲区内,密度、中子孔隙度等参数测量就无法进行精确的井眼校正,因此利用超声波测量井径存在一定的局限性。除此之外,密度测井的两个探测器也对仪器与井壁的间隙比较敏感。黄隆基[4]认为在密度测井中,间隙厚度、间隙填充物(泥浆)、地层密度会影响探测器测量的密度。Ellis等[5]认为密度测井的探测响应是地层密度和泥浆密度的综合加权,且权重与间隙厚度、间隙填充物(泥浆)类型有关。因此,研究随钻密度测井在各种井眼和间隙情况下的响应,可以得到间隙及井眼的精确计算关系,从而更好地弥补超声井径测量的不足。
本文针对随钻环境中的不同地层、仪器与井壁间隙及泥浆类型情况,利用蒙特卡罗程序构建仪器模型,利用实验数据对模拟结果进行了基准校正和刻度。研究了地层密度、泥浆密度和间隙尺寸对探测器响应的影响,通过分析得到间隙尺寸与远探测器测量密度、地层体积密度和泥浆密度之间的关系,并初步得到计算间隙尺寸公式和计算图版。另外,本文还利用随钻密度测井仪器在不同方位确定的仪器、井壁和间隙的几何关系,确定了井径计算方法。
1 随钻密度测井响应原理密度测井利用γ源向地层发射γ射线,γ射线经过康普顿散射被探测器接收,利用康普顿散射与被测物质密度的关系确定地层密度。随钻密度测井中使用137Cs作为γ源,其释放的0.662MeV的γ射线与岩石地层的相互作用中,康普顿效应占绝对优势。在理想情况下,测井仪器紧贴地层,则探测器的计数响应[6-7]:
| $N = {N_0}{{\rm{e}}^{\sigma \rho {d_{\rm{a}}}}} $ | (1) |
式中:N为探测器的计数率;N0为零源距的探测器计数率;σ为康普顿衰减系数;da为视源距;
而随钻密度测井在旋转过程中,由于受到间隙填充物(如泥浆、岩屑等)的影响,探测器探测的γ射线不完全来自地层的贡献,所以测量密度不等于地层真实密度[4-5],此时的γ射线衰减模型不再符合式(1)。从γ源释放的γ射线与泥浆、地层发生康普顿散射先后顺序:泥浆—地层—泥浆,最终被探测器接收。根据这相互作用的先后顺序,远探测器探测的γ射线计数与泥浆密度、地层密度的关系为:
| $ N = {N_0}{{\rm{e}}^{ - \sigma {\rho _{\rm{m}}}2{t_{\rm{m}}} - \sigma {\rho _{\rm{b}}}\left( {{d_{\rm{a}}} - 2{t_{\rm{m}}}} \right)}} $ | (2) |
式中:
| $ {\rho _{{\rm{far}}}} = \frac{{{\rho _{\rm{m}}}2{t_{\rm{m}}}}}{{{d_{\rm{a}}}}} + \frac{{{\rho _{\rm{b}}}\left( {{d_{\rm{a}}} - 2{t_{\rm{m}}}} \right)}}{{\left( {{d_{\rm{a}}} - 2{t_{\rm{m}}}} \right)}} $ | (3) |
将式(3)变形可以得到:
| $ {t_{\rm{m}}} = \frac{{{d_{\rm{a}}}\left( {{\rho _{\rm{b}}} - {\rho _{{\rm{far}}}}} \right)}}{{2\left( {{\rho _{\rm{b}}} - {\rho _{\rm{m}}}} \right)}} $ | (4) |
从式(3)可知,探测器测量到的密度不仅与地层密度相关,还与间隙尺寸、泥浆密度相关。根据式(4),只要地层密度与泥浆密度差值(介质密度差,用
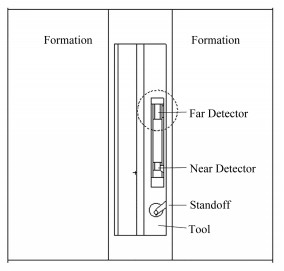
本文根据某公司研制的随钻密度测井仪,利用蒙特卡罗模拟程序(Monte Carlo N Particle Transport Code, MCNP)建立仪器、井眼、地层的三维模型,见图 1。其中远探测器的源距为39 cm,近源距为16.5 cm。用F8卡分别记录两探测器的脉冲幅度谱,取长短源距探测器的密度测量能窗为0.24~ 0.50 MeV;为了保证计算结果的可靠性,每次模拟时抽样109个光子,并利用DXTRAN球和Imp卡降低统计误差,使结果误差小于1%[7-8]。
|
图 1 随钻密度测井模型 Figure 1 Model of the drilling density log |
MCNP程序虽然克服了对空间-时间-能量-方向多维问题的系统复杂性的限制,但是模拟过于简单化、理想化,缺少基准的校正,计算的结果在统计性和准确性方面就存在问题。因此,要对蒙特卡罗模拟与实验结果进行基准检测研究[7-8]。
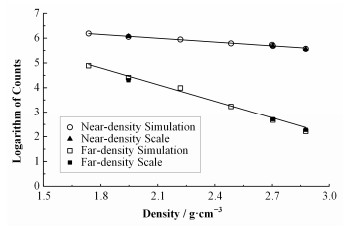
根据图 2所示,刻度的数据点是随钻密度测井仪器在标准刻度井中测量的数据,而模拟的数据点是利用MCNP程序模拟实际情况所测得结果,通过对比模拟结果与实际结果的数据,确定使用的计算模型,并进一步得到地层密度和近、远探测器的计数关系式(5)和(6)[9]。
| $ {\rho _{{\rm{near}}}} = - 0.515{\rm{ln}}{N_{{\rm{near}}}} + 7.078\;4 $ | (5) |
| $ {\rho _{{\rm{far}}}} = - 2.295{\rm{ln}}{N_{{\rm{far}}}} + 8.846\;2 $ | (6) |
|
图 2 探测器计数与地层密度之间关系 Figure 2 Relationship between experience density and detector counts |
式中:
远探测器测量的密度值反映了γ射线在地层和泥浆两种介质中的响应。为了能在复杂的井眼和地层环境得到精确的间隙计算公式,本文分别研究了间隙与介质密度差、间隙与测量密度差的关系。利用MCNP模拟了1~1.5g·cm-3的泥浆、孔隙度0%~30%饱和水的石灰岩、砂岩的地层情况。
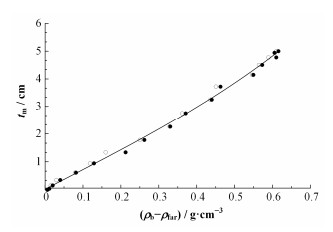
3.1.1 间隙对测量密度差影响为了详细研究间隙对测量密度差的影响,根据模拟数据建立介质密度差均为1.155g·cm-3,间隙尺寸与测量密度差的关系见图 3,横坐标表示测量密度差,纵坐标表示间隙尺寸。图 3中的空心圆代表密度为1 g·cm-3的淡水泥浆,孔隙度30%饱含水的砂岩地层;实心圆代表密度为1.393g·cm-3的轻泥浆,孔隙度8.5%饱含水的石灰岩地层。
|
图 3 间隙和测量密度差的关系 Figure 3 Relationship between the standoff and measurement density difference |
由图 3可知,在不同的地层、泥浆环境下,只要确定介质密度差不变,间隙厚度的增大会使测量密度差变大。间隙尺寸越大,γ射线在泥浆发生康普顿效应散射光子数越多,从而对远探测器计数贡献越大,则远探测器响应泥浆信息就越强烈。
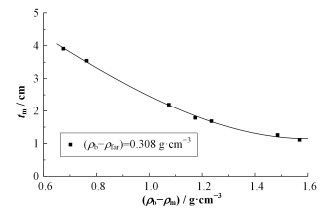
3.1.2 间隙与介质密度差的关系为了弄清间隙尺寸与介质密度差之间的关系,利用模拟数据建立图 4。图 4为测量密度差保持在0.308 g·cm-3时,间隙尺寸和介质密度两者之间的关系,其横坐标表示地层密度与泥浆密度差值,纵坐标表示间隙厚度
|
图 4 间隙与介质密度差的关系 Figure 4 Relationship of standoff and difference between formation density and mud density |
由图 4可知,当测量密度差保持一定时,间隙厚度越大,介质密度差就越小。当测量密度差保持一定时,说明γ射线经过泥浆发生康普顿散射的光子数对远探测器计数的贡献是保持一定;当间隙厚度越大时,泥浆对远探测器计数的贡献就增大;只有泥浆密度增大,被泥浆吸收的光子数越多,能保证泥浆对远探测器的计数贡献保持一定,这样介质密度差就越小。
通过分析图 3和图 4可以得到,当介质密度差确定时,间隙与测量密度差存在很好的函数关系,从而得到间隙的计算公式。结合图 3,通过数据拟合可以得到间隙尺寸的计算公式,即在
| $ {t_{\rm{m}}} = a{({\rho _{\rm{b}}} - {\rho _{\rm{far}}})^3} + b{({\rho _{\rm{b}}} - {\rho _{\rm{far}}})^2} + c({\rho _{\rm{b}}} - {\rho _{\rm{far}}}) + d $ | (7) |
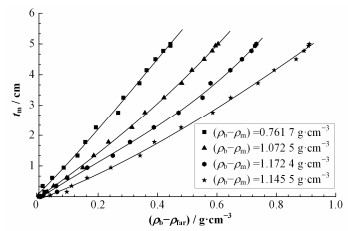
随钻密度测井在实际测量过程中,介质密度差时刻在变化,由于式(7)只是对于特定的介质密度差适用。为了确定在不同介质密度差情况下的间隙尺寸计算公式,根据模拟数据建立不同介质密度差的间隙尺寸计算图版,如图 5所示,通过数据拟合的方法可以得到在不同介质密度差情况下的间隙尺寸计算公式,类似于式(7)。
|
图 5 间隙的计算图版 Figure 5 Calculation chart for the standoff measurement |
图 5画出了介质密度差分别为0.762 g·cm-3、1.073 g·cm-3、1.174 g·cm-3、1.485 g·cm-3的情况下,间隙、测量密度差两者之间的关系。在实际的工程运用中,地层密度
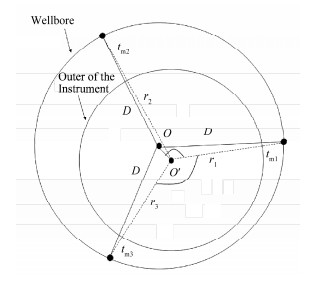
在随钻测井仪器在井下旋转过程中,仪器在井眼中难以避免会晃动,不能良好地贴壁,即仪器与井壁之间存在一定的间隙。在传统电缆测井中采用推靠器使其避免出现间隙,而在钻井过程中,仪器在高速旋转,无法使用推靠器[13]。本文利用仪器和井眼的几何关系来计算井径。其中:
| $ \begin{array}{l} {D^2} = {d^2} + S_1^2 - 2dS_1^2{\rm{cos}}\alpha \\ {D^2} = {d^2} + S_2^2 - 2dS_2^2{\rm{cos}}\left( {120^\circ - \alpha } \right)\\ {D^2} = {d^2} + S_3^2 - 2dS_3^2{\rm{cos}}\left( {120^\circ + \alpha } \right) \end{array} $ |
|
图 6 井眼和仪器几何关系示意图 Figure 6 Geometric diagram of borehole and tool |
对方程组进行求解得到井眼的半径D,结果如下:
| $ \begin{array}{c} {D^2} = \frac{{\left( {{S_1} + {S_2} + 3} \right){S_1}{S_2}{S_3}}}{{\left( {{S_2}{S_3} + {S_1}{S_3} + {S_1}{S_2}} \right)}} + \frac{{{{\left[{\left( {S_1^2-P} \right)/{S_1}} \right]}^2}}}{4} + \\ \;\;{\left[{\left( {S_2^2-P} \right)/{S_2}-\left( {S_3^2-P} \right)/{S_3}} \right]^2}/12\\ P = \left( {\left( {{S_1} + {S_2} + {S_3}} \right){S_1}{S_2}{S_3}} \right)/\left( {{S_2}{S_3} + {S_1}{S_3} + {S_1}{S_2}} \right) \end{array} $ |
其中,为了表示方便,设P是临时变量。
4 模拟结果与分析为了验证本文设计的间隙与井径计算效果。本文利用MCNP模拟了半径为10.4 cm的仪器分别在井眼半径为12.4 cm并充满淡水泥浆(1.000 g·cm-3)的5%孔隙的砂岩地层、充满轻泥浆(1.393 g·cm-3)半径为12.9 cm和孔隙度20%砂岩地层、充满淡水泥浆(1.000 g·cm-3)半径为13.4 cm的井眼和20%砂岩地层这三种情况下探测器的响应,远探测器接收的γ计数代入式(1)得到远密度,根据计数图版(5)选择计算间隙公式,从而计算井眼半径。
表 1为仪器在井眼半径(12.4 cm、12.9 cm、13.4 cm)模拟的结果,其中间隙的位置两两相隔120°。分析表 1,本文计算间隙的精度为±0.100 cm,井眼半径的精度为±0.090 cm,与超声井径仪在非盲区测量精度(0.100 cm)相差无几[15],这可以有效弥补超声井径仪在盲区的测量。
| 表 1 设计井眼半径、间隙与计算井眼半径、间隙的对比 Table 1 Comparison of designed borehole's radius, standoff and calculated borehole's radius, standoff |
根据随钻密度测井原理,使用了蒙特卡罗模拟,首先把地层的响应结果与前人实际测量的结果进行了基准校正,确保模拟数据的可行性,在此基础上来研究间隙尺寸、介质密度差、测量密度差三者的关系,通过分析,拟合得到计算间隙厚度的公式,使通过拟合公式计算出的间隙和井径的精确度达到了毫米级。本文所用的方法在超声测量的盲区内也能精确计算,弥补了超声井径仪的盲区的不足,可以为井径测量及各种测井方法的井眼校正提供更好的补充。
| [1] |
Yang C M, Jiang S B, Lin D Y, et al. An innovative ultrasonic time-of-flight measurement method using peak time sequences of different frequencies-part ⅱ:implementation[J]. IEEE Transactions on Instrumentation & Measurement, 2011, 60(3): 745-757. DOI:10.1109/TIM.2010.2063870 |
| [2] |
胡凯利.超声随钻井径检测仪方案设计和模拟与控制部分实现[D].荆州: 长江大学, 2014. HU Kaili. Ultrasonic design of drilling diameter detector and simulation and control part[D]. Jingzhou: Yangtze University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10489-1014345383.htm |
| [3] |
Paske W C, Mack S G, Rao M V, et al. Twist Sperry-sun drilling services-measurement of hole size while drilling[C]. Lafayette, Louisiana: SPWLA 31st Annual Logging Symposium, 1990.
|
| [4] |
黄隆基. 核测井原理[M]. 东营: 石油大学出版社, 2000. HUANG Longji. Nuclear logging principle[M]. Dongying: University of Petroleum Press, 2000. |
| [5] |
Ellis D V, Singer J M. Well logging for earth scientists[M]. Elsevier, 2007.
|
| [6] |
于华伟, 孙建孟. 蒙特卡罗模拟研究水平井密度测井中岩屑层的影响[J]. 核技术, 2009, 32(10): 751-755. YU Huawei, SUN Jianmeng. Monte Carlo simulation study of the influence of cuttings in horizontal well density logging[J]. Nuclear Techniques, 2009, 32(10): 751-755. |
| [7] |
于华伟, 孙建孟.水平井岩屑层对密度测井影响的蒙特卡罗模拟研究[C].全国核技术及应用研究学术研讨会大会, 2009. YU Huawei, SUN Jianmeng. Monte Carlo simulation of the influence of horizontal well cuttings on density logging[C]. National Conference on Nuclear Technology and Applied Research, 2009. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-HWLX200905001019.htm |
| [8] |
张丽, 孙建孟, 于华伟, 等. 不同井斜角情况下随钻密度测井探测特性[J]. 测井技术, 2013, 37(1): 31-34. ZHANG Li, SUN Jianmeng, YU Huawei, et al. Detection characteristics of logging while drilling under different well inclination angles[J]. Well Logging Technology, 2013, 37(1): 31-34. DOI:10.16489/j.issn.1004-1338.2013.01.005 |
| [9] |
Holenka J M, Evans M L, Kurkoski P L, et al. Logging while drilling method and apparatus for measuring standoff as a function of angular position within a borehole[P]. USA: US5513528A, 1996.
|
| [10] |
张锋, 韩忠悦, 吴赫, 等. 随钻脉冲中子伽马密度测井最佳源距的优化设计[J]. 同位素, 2016, 29(2): 93-97. ZHANG Feng, HAN Zhongyue, WU He, et al. Optimization design of the optimal source distance of the drilling pulse neutron gamma density logging[J]. Isotope, 2016, 29(2): 93-97. DOI:10.7538/tws.2016.29.02.0093 |
| [11] |
张丽, 孙建孟, 于华伟, 等. 重晶石泥浆对随钻密度测井中探测器能窗划分的影响[J]. 核技术, 2012, 35(11): 849-853. ZHANG Li, SUN Jianmeng, YU Huawei, et al. Influence of barite slurry on dividing the energy window of density logging detector with drilling[J]. Nuclear Techniques, 2012, 35(11): 849-853. |
| [12] |
Mickael M, Jones D, Phelps D. Standoff compensation and hole size correction of a new LWD density/neutron logging system[C]. Midland, Texas, US: SPE Technical Conference and Exhibition, 2002. DOI: 10.2118/77478-MS.
|
| [13] |
Best D, Wraight P, Holenka J. An innovation approach to correct density measurements while drillings for hole size effect[C]. SPWLA 31st Annual Logging Symposium, 1990. http://www.onepetro.org/conference-paper/SPWLA-1990-G
|
| [14] |
倪卫宁, 李三国, 李继博, 等. 基于超声测距的随钻井径测量系统设计[J]. 科技导报, 2013, 31(3): 48-51. NI Weining, LI Sanguo, LI Jibo, et al. Design of drilling diameter measurement system based on ultrasonic ranging[J]. Science & Technology Review, 2013, 31(3): 48-51. DOI:10.3981/j.issn.1000-7857.2013.03.006 |
| [15] |
刘之的, 李桂秋, 夏宏泉, 等. 随钻密度测井偏心影响校正方法研究[J]. 国外测井技术, 2007, 38(4): 43-44. LIU Zhidi, LI Guiqiu, XIA Hongquan, et al. Research on logging eccentricity influence correction method while drilling[J]. World Well Logging Technology, 2007, 38(4): 43-44. |


