2. 电子科技大学 资源与环境学院 成都 611731
2. School of Resources and Environment, University of Electronic Science and Technology, Chengdu 611731, China
航空γ能谱测量已成为主要的区域性航空物探方法之一,我国约80%大中型铀矿床是通过该方法发现的[1-2]。航空γ能谱测量结果强度低,矿致信号易与其他信息(岩性、土壤类型、湿度、植被覆盖密度和水域分布等诸多外界测量因素在探测器上响应)产生叠加[3-4],且受测量高度、大气氡浓度及宇宙射线等因素影响,测得的原始数据出现大量非矿致信息引起的异常,而矿致异常信息由于强度太弱,易被淹没于干扰信号中。对实测原始数据进行合理校正,是目前航空γ能谱测量亟待解决的问题。
对于航空γ能谱数据校正技术,目前学者主要以γ谱线解析为手段[5-7],致力于测量高度、地形和大气氡校正等前处理研究。Courbin[8]、Billings[9]、Eugene[10]等先后发表了定量反演问题的研究成果,而Brian[11]提出的三维(3 Dimensions, 3D)定量反演技术对航空γ能谱测量数据进行3D地形校正,取得了良好的应用效果;米耀辉等[12]结合航测动态测量特点,采用地形校正系数对航空γ能谱数据进行地形影响校正;孙海仁等[13]研究了大气氡变化对航空γ能谱测量的影响,提出三种排除大气氡干扰的方法;葛良全[14]、谷懿等[15]提出了基于改进谱线比法的航空γ能谱大气氡校正技术,有效校正了大气氡对航空γ能谱测量数据的干扰。
航空γ能谱测量载体——飞行器受地形、天气条件等因素的制约,野外飞行并不能全程保持匀速,导致航空γ能谱数据具有非均匀采样点距这一特性,且实测单点核素比活度值是该点沿测线方向相邻若干个非等距测点组成的区域核素比活度值的叠加结果。故测量结果易呈现出时域批次性特征,反映在等值图上则出现沿飞行测线的“条带状”异常分布,严重影响测量结果的准确性。而怎样合理地校正和滤除这些“条带状”假异常,目前国内外相关文献报道较少。
随着数字化地图的广泛使用和计算机图形学的不断发展,借鉴空间滤波等数字地图和数字图像处理理论,数据后处理技术成为航空γ能谱数据处理领域新的研究方向。本次研究采用基于小波变换的线单元校正法以调平测区内航空γ能谱原始测线数据,以单条测线为校正单元做小波域滤波处理,试图消除数据出现的“条带状”异常分布状况。目前在航空γ能谱数据中,学者多利用小波变换对谱线数据进行降噪[2-4],小波域方法在航空γ能谱数据后处理方法研究中报道较少。原理以各条测线上地质单元小波分解后近似信号值为背景值,用各条测线上相应地质单元段与该测线背景值的差值作为校正系数,尝试对相应测线内各点进行校正。
1 小波线单元校正方法由于航空γ能谱探测的目标为浅表地层介质中(土壤、岩石)的放射性核素值的分布与变化,探测器接收得到的均为非稳态数据信号。相较于傅里叶变换,小波变换具有多分辨率分析的特点,可根据需要任意调整观测尺度,对处理航空γ能谱数据这类结构复杂且非等间距、非稳态数据信号具有良好的适用性。
小波线单元校正法,是一种基于小波域的航空能谱测线数据调平方法。此方法将测区原始数据视作由若干条测线数据排列而成的一维数组,以测线为校正单元,通过对各一维数组进行不同尺度的小波分解、滤波和重构处理,达到校正测线数据目的。
小波变换的基本原理如下:设f(x)∈L表示一条航测线信号,x表示测点,ψ(x)表示小波基函数,则连续小波定义[16]:
| $ {\psi _{a, b}}(x) = \left| {\frac{1}{{\sqrt a }}} \right|\psi \left( {\frac{{x - b}}{a}} \right), \;\;a > 0;\;b \in R $ | (1) |
式中:ψa, b(x)为小波母函数;a为缩放因子;b为平移因子。令a=2j,b=ka,j∈Z,则可将连续小波变换离散化:
| $ {\psi _{j, k}}(x) = {2^{ - j/2}}\psi ({2^{ - j}}x - k) $ | (2) |
则离散小波变换为:
| $ W{T_f}(j, k) = \left\langle {f(x), {\psi _{j, k}}(x)} \right\rangle \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = {2^{ - j}}\int {f(x)\psi ({2^{ - j}}x - k){\rm{d}}x} $ | (3) |
通常使用现有的尺度函数φ(x)和小波函数ψ(x)。
航空γ能谱野外实测飞行中,时域批次性干扰产生的原因有如下两点:1)航空γ能谱为非定点测量,探测器每秒测量并记录一个全谱数据,受飞行测区地形制约,航测工作中不可能保持全程匀速,导致实测值并非全球定位系统(Global Positioning System, GPS)定位单点核素比活度值,而是定位点沿测线方向相邻若干非等距测点的核素比活度值的综合反映;2)测线之间由于测量飞行区域大,每条测线距离,同一区域相邻测线间的飞行时间间隔较大,而测量受多种因素影响,导致不同测线间的数据出现明显的阶梯效应。
由于异常信息在频域上对应为细节信号,而背景对应为近似信号。测线数据经多重小波分解后可分为若干个不同尺度的细节部分和一个近似部分,该近似部分可视为地质背景信息和“条带状”假异常信息的叠加。航空γ测量在矿产资源勘查重点关注异常信息,即小波分解后的细节部分,故从异常信息提取角度看,可将近似部分滤除。
2 小波基函数的选取不同的小波基函数和分解层数会导致不同的效果,仅凭肉眼无法分辨出分解效果的优劣,这里选取标准差变异系数判断小波分解后是否达到最优分解层数。由于成矿区域均处于高变异系数区[17-18],γ能谱的变异系数可反映测区U、Th、K含量的变化程度,因此可用于研究放射性元素的空间分布差异、普查找矿及远景预测。在航空γ能谱数据异常提取中一般采用标准差变异系数CV (Coefficient of Variation)[18-19]衡量数据离散程度,预测成矿概率,其计算公式如式(4)所示。
| ${\rm{CV}} = \frac{{\sqrt {\frac{1}{{n - 1}}\sum\limits_{j = 1}^n {({X_i} - \bar X} {)^2}} }}{X} $ | (4) |
式中:
航空γ能谱数据为离散数据,故应选取可进行离散小波变换的小波基函数进行分析。目前常用的可处理离散数据的小波基函数有5种,特点如表 1所示。
| 表 1 小波基函数特点对比 Table 1 Comparison of wavelet base functions |
由于dbN小波不具有对称性,重构时会产生相位失真,故对symN、coifN、biorNr.Nd和rbioNr.Nd小波进行对比,选取最优小波基函数。
使用小波线单元校正法对测线进行校正流程:
1) 选取小波基函数,利用式(3),对单条测线进行小波变换;
2) 将小波变换后的高频部分进行重构;
3) 计算重构后测线的变异系数;
4) 增加分解层数,重复步骤1)、2),直到达到测预设的分解层数。由于小波分解迭代算法为下采样,每迭代一次数据量减少一半,故预设分解层数根据测线数据量而定,不可设置过大;
5) 选取变异系数发生突变前的分解层数为最优分解层数,逐条对原始测线进行校正。
3 结果与分析 3.1 仪器与测区概况选取内蒙古某金属矿测区1:50000航空放射性野外试生产数据(仪器为成都理工大学自主研发的AGS863航空γ能谱仪)中铀元素含量作为数据源。测区地质简图如图 1所示。区内主要以花岗岩、砂岩和火山碎屑沉积岩为主,测区东南部有金属矿点(铅锌矿、铁矿)分布。AGS863航空γ能谱仪采用两箱,每箱由5条4L装阵列式NaI晶体探测器组成(其中1条上视晶体进行宇宙射线与大气氡浓度监测)。探测器安装在Y-12型运输机上。测量平台搭载数据采集系统、无线电测高仪、GPS等。测区面积约300km2,设计测线21条,测点6705个。铀含量均值为3.968 μg·g-1,最高值为37.204 μg·g-1,最低值为0.049 μg·g-1,标准偏差为3.186 μg·g-1。
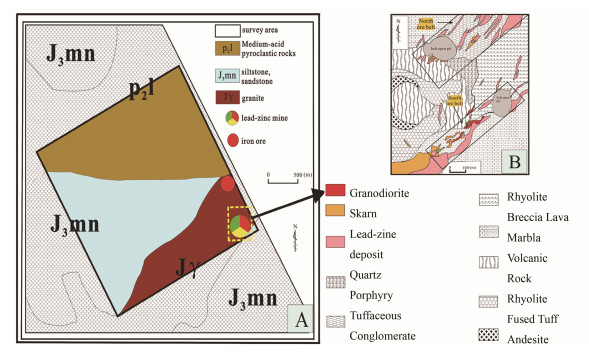
|
图 1 测区地质(A)和地面查证区域地质(B)简图 Figure 1 Geological map of the unsurveyed area (A) and anomaly inspection area (B) |
选取symN、coifN、biorNr.Nd和rbioNr.Nd典型离散小波基函数进行对比。测线选取“条带状”最严重的第20号测线,最大分解层数依据测点数量设定为6。处理后的变异系数如表 2所示。
| 表 2 变异系数分解表 Table 2 Coefficient of variation decomposition table |
表 2中,变异系数最高值为1.00665,对应为rbio3.7的4层分解。为更直观体现变异系数的变化趋势,将变异系数绘制折线图,如图 2所示。
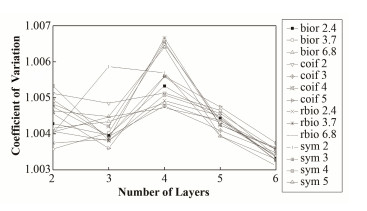
|
图 2 变异系数对比 Figure 2 Coefficient of variation comparison chart |
图 2中,同一小波基函数中,随着分解层数的增加,变异系数大多数的变化趋势为先增后减,在4层分解处达到极值。4层分解后,可将原测线的高、低频部分较为完整地分离。在4层分解时,rbio3.7的变异系数最大,且变化最为剧烈。故选取rbio3.7为小波基函数,逐条对测线进行4层分解并对高频部分重构。rbio3.7的尺度函数和小波函数图如图 3所示,校正前后某测线对比图如图 4所示。
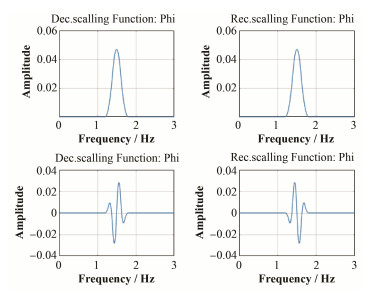
|
图 3 rbio3.7的尺度函数和小波函数 Figure 3 Scale and wavelet functions of rbio3.7 |
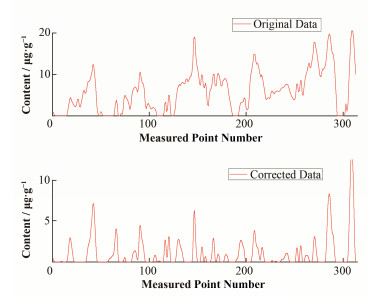
|
图 4 校正前后对比图 Figure 4 Comparison of original data and corrected data |
由图 4可知,校正前后测线中铀含量整体趋势保持一致。校正前部分测点出现剧烈不规则波动,且140号测点、260号测点附近比活度呈平台状;校正后波动处部分区域变为平稳,高值区域峰形基本不变,测线中平台状异常点消失。
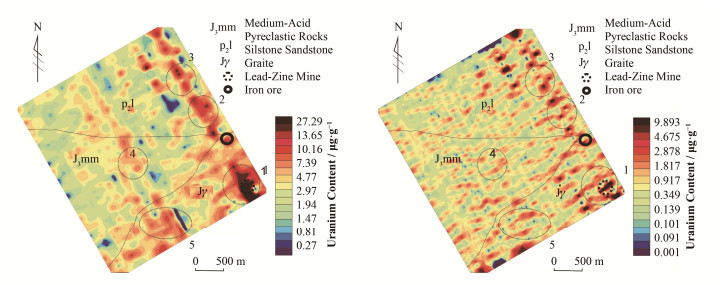
3.3 校正结果与分析使用克里金网格化法分别对实测原始离散点位数据、4层rbio3.7分解线单元校正数据进行(128×128)空间插值,参照《EJ-T 1032-2005航空伽玛能谱测量规范》绘制等值线图(图 5)。
|
图 5 原始铀(a)和校正后铀(b)含量等值线图 Figure 5 Isogram of original uranium (a) and corrected uranium (b) contents |
图 5(a)中,由于时域批次性的影响,1~4号区域皆出现了不同程度的条带状异常分布。其中1号区域由于金属矿点的存在,矿致异常与条带状假异常叠加并连接成片,呈现出长椭圆状的异常区域;2、3、4号区域出现了不规则连接成片的异常区域,呈现出沿航测线分布的条带状异常形态;5号区域出现因数据畸变产生的条带状正、负异常区域沿测线方向相邻分布。这些条带状异常明显为非矿致异常造成的大范围干扰信息,且与矿点异常叠加,对矿致异常识别和下一步异常查证工作造成严重干扰。
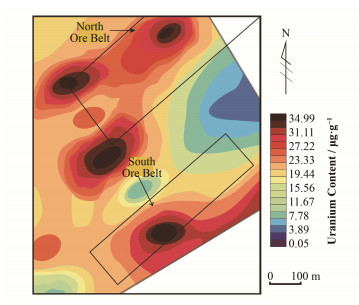
图 5(b)中,原始测线数据经小波线单元校正法校正后,1号区域连接成片的异常带被划分为两个小范围强异常,呈近似“C”型;将其与1号区域航空γ能谱地面异常查证结果等值线图(图 6)进行比较,发现相比于原始数据所呈现的异常信息,经小波线单元校正法处理后的异常形态、矿致异常点位置和异常区范围等信息均与地面查证结果保持一致,说明小波线单元校正法能滤除因时域批次性造成的条带状假异常信息,准确地从带干扰的数据中识别航空γ能谱矿致异常信息;2、3、4号区域经地面查证均为无异常的航空伽马能谱条带状假异常分布区,经小波线单元校正法校正后,条带异常强度和范围明显降低,但假异常的浓集趋势并未被完全滤除;5号区域经处理后条带状负异常完全消失,正异常范围减小,但异常强度和背景值基本保持不变,可以看出线单元校正法可在保持地质背景信息基本不变的前提下修正因测线数据畸变引起的异常。
|
图 6 航空伽马能谱地面异常查证铀等值图 Figure 6 Uranium isogram of airborne gamma spectrum ground anomaly inspection |
小波线单元校正法,利用标准差变异系数选取最优小波基函数及最优分解层数,避免了主观因素对小波选取的影响;利用选取的小波基函数对测线进行小波变换,校正了时域批次性对探测结果的影响。结果表明:原始数据经校正后,矿致异常位置清晰准确,异常面积减小,矿点周围因时域批次性造成的干扰信息消失,条带异常强度和范围明显降低,数据畸变造成的假异常信息滤除,客观地还原了测区内的放射性核素分布情况,缩小矿致异常信息范围,为下一步勘查工作的开展提供了可靠的信息支持。
针对2、3、4号区域条带状假异常的浓集趋势并未被完全滤除的局限性及垂直测线方向的条带异常未完全滤除,下一步考虑在小波域滤波尺度的选择和小波重构算法的改进这两方面作进一步优化,以增强航空伽马能谱异常信息线单元校正方法的适用性。
| [1] |
万建华, 熊盛青, 范正国. 航空伽马能谱测量方法技术现状与展望[J]. 物探与化探, 2012, 36(3): 386-391. WAN Jianhua, XIONG Shengqing, FAN Zhengguo. The status and prospects of airborne gamma-ray spectrometry technology and its application[J]. Geophysical and Geochemical Exploration, 2012, 36(3): 386-391. |
| [2] |
刘裕华, 顾仁康, 候振荣. 航空放射性测量[J]. 物探与化探, 2002, 26(4): 250-252. LIU Yuhua, GU Renkang, HOU Zhenrong. Airborne radiometrics survey[J]. Geophysical and Geochemical Exploration, 2002, 26(4): 250-252. DOI:10.3969/j.issn.1000-8918.2002.04.002 |
| [3] |
葛良全, 熊盛青, 曾国强, 等. 航空伽马能谱探测技术与应用[M]. 北京: 科学出版社, 2016. GE Liangquan, XIONG Shengqing, ZENG Guoqiang, et al. Airborne gamma-ray spectrum detection and application[M]. Beijing: Science Press, 2016. |
| [4] |
熊超.航空伽马能谱异常信息提取方法研究[D].成都: 成都理工大学, 2016. XIONG Chao. The research on anomaly information extraction method of airborne gamma-ray spectrum survey[D]. Chengdu: Chengdu University of Technology, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10616-1016226771.htm |
| [5] |
张庆贤, 葛良全, 谷懿, 等. 基于极大似然估计的NaI(Tl)晶体仪器谱解析方法研究[J]. 核技术, 2011, 34(8): 569-574. ZHANG Qingxian, GE Liangquan, GU Yi, et al. The unfolding of NaI(Tl) γ-ray spectrum based on maximum likelihood method[J]. Nuclear Techniques, 2011, 34(8): 569-574. |
| [6] |
吴和喜, 葛良全, 罗耀耀, 等. 基于最小二乘法的航空伽马能谱解析[J]. 核技术, 2016, 39(11): 110201. WU Hexi, GE Liangquan, LUO Yaoyao, et al. Analyzing airborne gamma-ray spectrum by the least square method[J]. Nuclear Techniques, 2016, 39(11): 110201. DOI:10.11889/j.0253-3219.2016.hjs.39.110201 |
| [7] |
吴和喜, 葛良全, 魏强林, 等. 航空伽马能谱仪无源效率刻度方法研究[J]. 核技术, 2016, 39(12): 120202. WU Hexi, GE Liangquan, WEI Qianglin, et al. Methodology study on the sourceless efficiency calibration of airborne gamma-ray spectrometry[J]. Nuclear Techniques, 2016, 39(12): 120202. DOI:10.11889/j.0253-3219.2016.hjs.39.120202 |
| [8] |
Courbin F, Magain P, Kirkove M, et al. A method for spatial deconvolution of spectra[J]. OALib Journal, 1999, 529(2): 1136-1144. DOI:10.1086/308291 |
| [9] |
Billings S D, Minty B R, Newsam G N, et al. Deconvolution and spatial resolution of airborne gamma-ray surveys[J]. Geophysics, 2003, 68(4): 1257-1266. DOI:10.1190/1.1598118 |
| [10] |
Eugene D. Processing of airborne gamma-ray spectrometry using inversions[C]. 25th International Geophysical Conference and Exhibition, 2016: 1033-1040. http://www.publish.csiro.au/EX/ASEG2016ab147
|
| [11] |
Brian M, Ross B. The 3D inversion of airborne gamma-ray spectrometric data[C]. Exploration Geophysics, 2016, 47(2): 150-157. http://www.publish.csiro.au/?paper=EG14110
|
| [12] |
米耀辉, 范正国, 周锡华, 等. 航空伽马能谱测量地形影响改正实现方法[J]. 物探与化探, 2013, 37(6): 1034-1038. MI Yaohui, FAN Zhengguo, ZHOU Xihua, et al. The terrain correction method for airborne gamma-ray spectrometry survey[J]. Geophysical and Geochemical Exploration, 2013, 37(6): 1034-1038. DOI:10.11720/j.issn.1000-8918.2013.6.15.issn.1000-8918.2013.6.15 |
| [13] |
孙海仁, 李毅, 曾晶荣, 等. 大气氡变化对航空伽马能谱测量的影响[J]. 物探与化探, 2017, 41(2): 283-290. SUN Hairen, LI Yi, ZENG Jingrong, et al. The influence of the radon on the airborne gamma-ray spectrometry survey[J]. Geophysical and Geochemical Exploration, 2017, 41(2): 283-290. DOI:10.11720/wtyht.2017.2.14 |
| [14] |
葛良全, 谷懿, 张庆贤, 等. 航空伽马能谱测量谱线比法大气氡校正的理论研究[J]. 核技术, 2010, 33(11): 844-848. GE Liangquan, GU Yi, ZHANG Qingxian, et al. Radon background correlation using spectral-ratio method in natural gamma-ray spectrometry[J]. Nuclear Techniques, 2010, 33(11): 844-848. |
| [15] |
谷懿, 葛良全, 熊盛青, 等. 基于康普顿散射本底扣除的航空伽马能谱测量谱线比大气氡校正方法[J]. 原子能科学技术, 2014, 48(1): 147-151. GU Yi, GE Liangquan, XIONG Shengqing, et al. Spectral-ratio radon background correction method in airborne gamma-ray spectrometry based on Compton scattering deduction[J]. Atomic Energy Science and Technology, 2014, 48(1): 147-151. DOI:10.7538/yzk.2014.48.01.0147 |
| [16] |
IngridDaubechies. 小波十讲[M]. 北京: 国防工业出版社, 2011. Ingrid Daubechies. Ten lectures on wavelets[M]. Beijing: National Defend Industry Press, 2011. |
| [17] |
孙中任. 变异系数用于标本磁参数统计工作的研究[J]. 地质与勘探, 2009, 45(1): 65-69. SUN Zhongren. Study on usage of coefficient of variation for statistics of magnetic parameters of samples[J]. Geology and Prospecting, 2009, 45(1): 65-69. |
| [18] |
张文斌, 熊盛青. 一种有用的解释参数——航空伽玛能谱变异系数[J]. 物探与化探, 1990, 14(4): 276-284. ZHANG Wenbin, XIONG Shengqing. Airborne gamma-ray spectrometric variation coefficient-a useful parameter for interpretation[J]. Geophysical and Geochemical Exploration, 1990, 14(4): 276-284. |
| [19] |
Cressie N. Statistics for spatial data[J]. Terra Nova, 1992, 35(3): 321-323. |


