自由电子激光(X-ray Free-Electron Laser, XFEL)是目前世界上最亮的X射线光源，其最主要的特点是能产生超快（飞秒）的X光脉冲，并且具有极高的相干性和极高的亮度。XFEL的出现促使实验新技术的进一步发展，如X射线关联谱^[1-2]、相干衍射成像^[3-4]、X射线相衬成像^[5]等。脉冲相干性信息是开展先进实验以及科研人员准确提取样品结构的前提条件，此外，XFEL横向相干性测量作为一种束流诊断方法用于监测电子束横向分布结构，提供装置的运行状态等信息^[6]。所以准确测量XFEL的相干性，对XFEL装置运行和用户提供光脉冲相干性信息是非常必要的，也是本文重要的研究内容。

光场的横向特性通常使用物理量横向相干长度来描述，现代光学定义了更一般的复相干函数(Complex Coherence Function, CCF)来描述其横向相干性^[7]。目前测量XFEL和同步辐射横向相干性的实验方法主要分为两类^[8]：分波前干涉法，如经典的杨氏双缝干涉仪、光栅的方法等。此类方法可直接获得光的相干性信息，但需多次改变实验参数（双缝间距、探测距离等）来获得不同空间位置的相干性^[9-10]；强度关联法，如Hanbury Brown-Twiss强度干涉仪。这种方法测量系统简单，但无法实现单发脉冲相干性测量，同时光强度分布容易受到光学元件表面粗糙度及其安装精度的影响^[11-12]。外差散斑技术是一种测量系统简单、可实现单发脉冲二维相干性获取的实验方法。此方法在2009年由Alaimo提出^[13]，并用于测量同步辐射的横向相干性，而后推广到可见光波段SASE-FEL^[14]。

自放大自发辐射模式(Self-Amplified Spontaneous Emission, SASE)是XFEL的基本运行模式之一，这种模式下XFEL光输出功率极不稳定且强度分布极不均匀。目前国内已经建成上海软XFEL，但对其光脉冲的空间相干性研究还是空白。因此，本文研究使用近场外差散斑技术测量SASE-XFEL单发脉冲横向相干性问题，为克服SASE-XFEL输出功率不稳定和强度分布不均匀对复相干函数测量(Complex Coherence Function, CCF)的影响^[13-14]，首次提出“孪生测量”的实验方案。该方案把每束光脉冲平均分为两束，其差值信号只与外差散斑信号有关，从而有效提取出外差散斑信号。通过建立外差散斑的动力学模型，结合SASE模式的上海软XFEL，利用Genesis、光学传播软件(Optical Propagation Code, OPC)和MATLAB，数值仿真了单粒子、多粒子的外差散斑，分析了这种方案的可行性。可以期望这种测量方案在将来上海软X射线自由电子激光以及国际上的自由电子激光装置上得到实际应用。

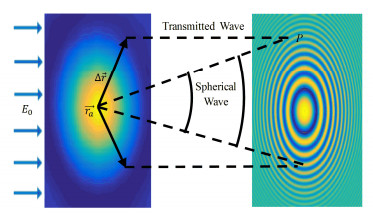
当一束相干光E₀照射在单个粒子上时，粒子散射球面波与较强的透射波在空间产生叠加效应。在近场区域内，透射波受散射球面波的外差调制，形成圆形外差干涉条纹^[15]，如图 1所示。条纹可见度与其互强度函数(Mutual Intensity Function, MIF)J的模相关，J表示为^{[7, 16]}：

图 1

图 1 透射波与散射波的干涉条纹，P点条纹可见度与复相干函数$\mu (\overrightarrow {{r_a}}, \overrightarrow {{r_a}} + \Delta r)$的模相关 Figure 1 Interference fringe between a spherical wave and a single coherent patch. The visibility of point P is relevant to the modulus of $\mu (\overrightarrow {{r_a}}, \overrightarrow {{r_a}} + \Delta r)$

式中：${E_0}(\overrightarrow {{r_a}} )$表示位置处$\overrightarrow {{r_a}} $的光场复振幅；$\Delta \overrightarrow r $表示相对横向位移；尖括号〈…〉代表脉冲统计平均值，通常也等于时间平均值^[16]。互强度函数描述了粒子所在位置光场与周围其他所有横向位置光场的关联性，对应归一化复相干函数(CCF)表示为μ：

式中：${I_0}(\overrightarrow {{r_a}} )$表示位置$\overrightarrow {{r_a}} $处的光场强度；${I_0}(\overrightarrow {{r_a}} {\rm{ + }}\Delta \overrightarrow r )$表示$\overrightarrow {{r_a}} {\rm{ + }}\Delta \overrightarrow r $处的光场强度。

但单粒子散射信号太弱，通常使用大量粒子悬浮液获得可测的信号强度。大量单粒子外差干涉信号的叠加形成近场外差散斑，其傅里叶空间功率谱包含了相干性信息，由此获得距离光源${Z_0}$、样品位置处的互强度函数。对于粒子悬浮液，探测器位置光场强度$I(\overrightarrow r )$表示为^{[6, 14]}：

其中：${E_s} = \sum\nolimits_{a = 1}^N {\frac{{S(0)}}{{k{R_a}}}} {E_0}(\overrightarrow {{r_a}} ){{\rm{e}}^{ik{R_a}}}$；$k = \frac{{2\pi }}{\lambda }$表示波数；${R_a}$表示粒子中心$\overrightarrow {{r_a}} $到探测点$\overrightarrow r $的距离；$S(0)$表示粒子的形状因子^[17]；$\Re e$为取复数的实部；${I_0}$表示透射强度。散射波之间的交叉项已忽略^{[6, 14-15]}。式(3)第二项表示外差信号，其傅里叶空间功率谱I(q)正比于互强度函数J的平方和^[14]：

其中：动量转移$\overrightarrow q {\rm{ = }}2k\sin (\theta /2)$，$\theta $表示散射角，$k$是波数；$\Delta \overrightarrow r = z\overrightarrow q /k$；$z$表示探测器与样品之间距离，理论和实验已证明式(4)第二个等式在粒子数很大时成立^{[7, 14]}。$\widetilde J$为平均互强度函数，表示所有散射粒子位置处的互强度函数的平均值，仅是相对横向距离的函数，因傅里叶功率谱未保留与粒子位置有关的相位信息。考虑到探测器的传递函数$H(q)$以及噪声、杂散信号$P(q)$等，外差信号的功率谱$I(\overrightarrow q )$为：

其中：$T(\overrightarrow q ) = {\sin ^2}(\frac{{{q^2}z}}{{2k}})$；$S(\overrightarrow q )$表示实际粒子的形状因子^{[14, 17-18]}（通常适当选择布朗粒子大小使其在所考虑的动量范围内近似为常数1，可记为$S(0)$=1）。

探测器传递函数$H(q)$，噪声、杂散信号$P(q)$可用相同实验装置测量，$S(q)$可通过米氏散射理论(Mie Theory)^[17]计算或由实验测量。一旦得到了式(5)中的这些项，平均互强度函数的模方由振荡项${\left| {\widetilde J(\Delta \overrightarrow r )} \right|^2}T(\overrightarrow q )$的包络确定^{[6, 14, 19]}。

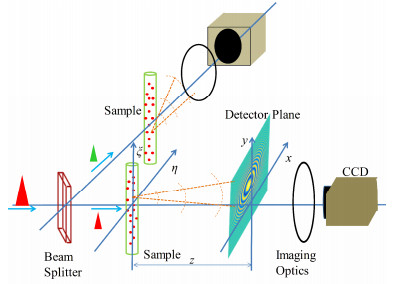
基于上述原理，获取近场外差散斑信号是此方法的关键，但基于SASE的软XFEL光输出不稳定性和光强度分布极不均匀不利于近场外差干涉信号的提取和平均复相干函数的测量^[20]。为有效获得外差信号，提出“孪生测量”的实验方案，如图 2所示。

图 2

图 2 “孪生测量”的实验方案 Figure 2 Diagram of twin measurement experimental setup

选择将布朗粒子的悬浮液盛在两个相同的毛细管中，其与分束镜(Beam Splitter)的距离相等，与探测相机(Charged Couple Device, CCD)的距离都等于$z$，改变测量距离$z$值可在不同距离上得到复相干函数。实际上，近场外差的实验条件如下^{[13, 20]}：

1) 布朗粒子横向尺寸小于XFEL光场的横向相干长度${\sigma _{\rm{c}}}$（约是光束的横向尺寸）且粒子散射光场分布在散射角${\theta _{\rm{s}}}$内，${\theta _{\rm{s}}}z \gg {\sigma _{\rm{c}}}$；

2) 探测距离在光场相干面积$\sigma _{\rm{c}}^2$的近场区域以内，$z$≪k$\sigma _{\rm{c}}^2$；

3) 散射强度约为入射光强的$1\% $等。

在上述条件下，外差散斑的强度分布可认为是大量随机单粒子干涉条纹的叠加，散斑信号的功率谱与平均复相干函数相关。基于以上测量方案，获得散斑信号的基本方法是：单发的XFEL光脉冲信号被分成等幅值的两束（或者幅值成比例的两束脉冲），分别照射在两个统计独立的粒子悬浮液上。因两组粒子的统计性不同，同时采集到两组CCD信号强度分布不同，其差值信号不依赖于透射强度，只与散射信号相关。此外，粒子系统是统计独立的，两组散斑信号强度可认为是相互独立^{[13, 21-22]}。每个单发脉冲都对应两组信号，如果$f({\vec r_1},z)$和$f({\overrightarrow r _2}, z)$表示采集到的两组强度分布，外差散斑信号表示如下：

式中：$\overrightarrow r 1$、$\overrightarrow r 2$表示两个CCD上的横向位置。散斑信号的傅里叶空间功率谱$I(\overrightarrow q, z)$正比于平均互强度函数的模方，$I(\overrightarrow q, z)$表示为：

考虑到XFEL强度分布不均匀性对平均互强度函数归一化的影响，适当选择毛细管的直径使得布朗粒子处于光强近似均匀处。利用CCD采集到的强度信号，实时计算光场的强度关联函数^{[14, 20]}${A_l}(\Delta \overrightarrow r ) = \langle I(\overrightarrow r )I(\overrightarrow r + \Delta \overrightarrow r )\rangle $，其中：$I(\overrightarrow r )$为布朗粒子处的透射光强；$I(\overrightarrow r + \Delta \overrightarrow r )$表示其他位置的强度。平均复相干函数$\widetilde \mu $的模可如下得到：

将要建成的上海软X射线自由电子激光(Shanghai Soft X-ray Free Electron Laser, XFEL)用户装置是我国的第一台基于自放大自发辐射(Self-Amplified Spontaneous Emission, SASE)和种子模式(Seeds Mode)的软X射线自由电子激光装置^[23]，全长540m，其工作波长范围为2~10nm。SASE模式是基于在磁场中做横向周期性运动的相对论性电子束与其自发辐射场之间的相互作用。光阴极发射出的电子束团经直线加速段加速到最终能量为1.5GeV，而后注入波荡器中（波荡器共10节，每节周期为16mm，总长度40m）。用户装置直线加速段的主要参数：电子束能量1.5 GeV，束团电荷量0.5 nC，能散（均方根）≤0.1%，束团长度≤0.7 ps，归一化发射度≤1.5 mm·mrad，重复频率50 Hz，辐射波长1.922 nm，峰值流强≥700 A。其中，辐射带宽$\Delta \lambda /\lambda $与波荡器的周期数有关，为$1\%$，由此可以估算光脉冲的纵向相干长度${l_{\text{c}}} = {\lambda ^2}/2\Delta \lambda $=192nm，大于仿真中最大光程差$\Delta l = {L^2}/(2z) = $69nm（$L$取300μm，z取650mm），仿真计算可忽略纵向相干效应^[20]。由以上数据以及波荡器参数等，用FEL模拟软件Genesis，仿真计算上海SASE-SXFEL用户装置光场输出，如图 3所示。

图 3

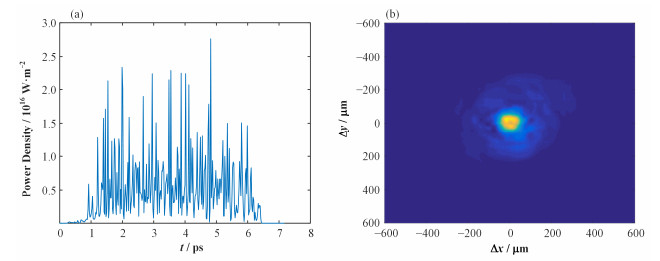
图 3 脉冲功率的时间分布(a)和光场空间强度分布(b) Figure 3 Temporal distribution of a single radiation (a) and spatial intensity distribution of a single pulse (b)

由图 3(a)可见，源于束团电荷密度涨落的SASE-SXFEL输出功率是极不稳定的，体现出SASE模式的特点。辐射场的光脉冲长度约是550fs，比电子束纵向长度稍短。此外，还表明XFEL辐射场可看成准静态随机过程，Wiener-Khinchine定理成立^{[7, 24-25]}。该定理指出准静态随机变量的功率谱密度可通过其时间关联函数（纵向相干函数）进行傅里叶变换得到，但这里只考虑横向相干性。

图 3(b)表示波荡器末端的光脉冲强度分布。光强在横向上是极不均匀的，主要分布在中心位置且空间对称，这是因为电子束团横向对称分布，束团发射度很小且辐射场具有较高的相干性^[16]。辐射光强的水平与垂直尺寸是120μm（半高全宽）。

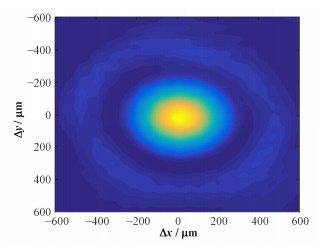
通常实验装置距波荡器有一定距离，得到Genesis模拟计算的光场复振幅数据后，利用光学传播软件OPC计算距波荡器任意位置的光场分布。以距波荡器30m位置为例，该位置对应测量方案中分束镜(Beam Splitter)位置。OPC的结果显示光场的水平、垂直尺寸在传播中有所增加，分别为604.8μm和600μm，呈圆对称性分布，横向强度近似均匀尺寸为200μm，见图 4。

图 4

图 4 OPC输出光强分布 Figure 4 Intensity distribution from OPC

为验证测量方案的可行性，基于测量方案和实验条件，利用MATLAB软件编程仿真探测器CCD上采集到的两组信号。限于计算能力，光场的横向尺寸同比例缩小一半，分别为302.4μm（水平）和300μm（垂直），有效像素大小为0.5μm，布朗粒子大小为0.45μm，粒子透射率为99%。仿真采用如下简化的散射模型：1)布朗粒子随机分布在二维平面上；2)不考虑粒子对X射线的吸收，暂不考虑溶剂的影响；3) X射线仅被散射一次，即单粒子散射；4)由于探测器的传递函数以及噪声等无法建立对应的物理模型，仿真中暂不考虑这些因素。

首先考虑单粒子情形。在上述条件下，仿真计算样品与探测器相距650mm位置处单粒子的外差信号，如图 5(a)所示。

图 5

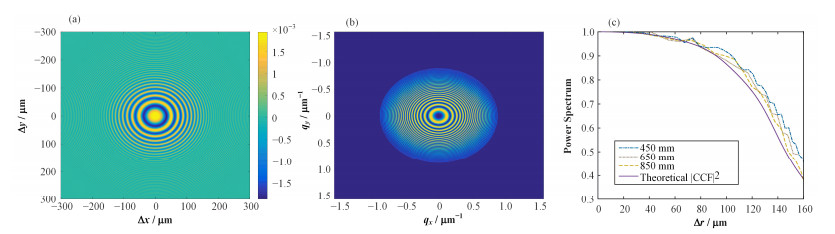
图 5 单粒子近场外差信号(a)、单粒子外差信号功率谱(b)和不同探测距离下径向复相干函数的模方(c) Figure 5 Near-field heterodyne signal particle (a), power spectrum of heterodyne signal from single particle (b) and radial profile of the squared modulus of complex coherence function for different distances (c)

结果表明：XFEL横向相位分布产生的单发脉冲XFEL外差信号近似是圆形的。相干性信息可由傅里叶功率谱得到，如图 5(b)所示。功率谱呈圆对称分布，且有明显的振荡现象，其振荡包络为互强度函数的模方。样品位置处光场横向相干性是确定的，因而在不同探测距离$z$上，散斑的傅里叶功率谱的包络对应相同的复相干函数的模方，如图 5(c)所示。图 5(c)表明距离光场中心160μm处（真实尺寸320μm处），复相干函数数值为0.65，而光场横向尺寸为600μm。仿真不同位置的复相干函数，得到总横向相干度$\zeta $为0.97。$\zeta $是归一化的平均横向相干函数$\widetilde \mu {\rm{(}}\overrightarrow r {\rm{1, }}\overrightarrow r {\rm{2)}}$的光强度加权平均值，其定义为：

式中：$I(\overrightarrow r 1)$和$I(\overrightarrow r 2)$为透射强度。XFEL光场具有极好的横向相干性。图 5(c)中计算与理论的曲线有偏差，主要是计算曲线考虑了粒子的散射与透射。

仿真计算多粒子外差散斑信号如图 6(a)所示，傅里叶功率谱如图 6(b)所示。图 6表明，多粒子产生的外差散斑相比于单粒子散斑，信号强度明显增大且散斑分布具有随机性，而其傅里叶功率谱具有明显的振荡现象。限于计算能力和使用的简化散射模型，多粒子仿真下没有重现实验上与粒子位置有关的相位之间抵消作用^{[7, 14]}，因而未得到有效的数值结果。真实实验散斑的产生必须考虑粒子的空间分布，大量空间分布粒子的位置相位相互抵消^{[7, 14]}，式(4)中第二个等式严格成立。在除去式(5)中传递函数H和噪声$P$后，傅里叶功率谱的包络正是平均互强度函数的模方^[14]，归一化后得到平均复相干函数的模，获得光场二维相干性信息。

图 6

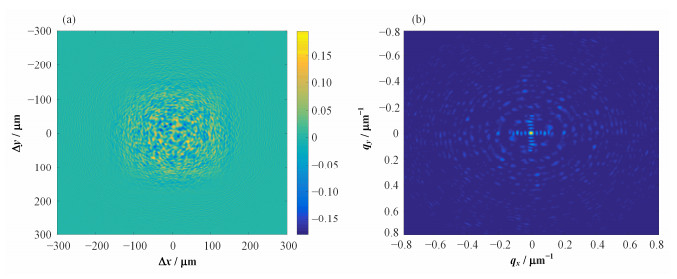
图 6 多粒子外差散斑(a)和傅里叶功率谱(b) Figure 6 Speckle field from colloidal particles (a) and Fourier space of the speckle field (b)

本文首次提出了基于近场外差散斑“孪生测量”的实验方案，该方案采用两组统计独立粒子系统的差值提取外差散斑信号，并使用Genesis、OPC和MATLAB编程仿真计算了单发光脉冲的单粒子和多粒子外差散斑，获得了单粒子情形的横向相干性。结果表明：此方案适用于SASE-SXFEL横向相干性测量。单粒子外差散斑的傅里叶功率谱有明显的振荡现象，其包络曲线归一化后表示复相干函数的模方，结果与理论曲线符合得很好。多粒子外差散斑信号有一定的随机性，但傅里叶功率谱表现有规律的振荡，多粒子情形并没有得到很好的数值结果，但多粒子情况只是单粒子的推广，很容易看出其原理和单粒子类似。从更实际的角度看，仿真计算还有许多可以改进的地方，考虑分束镜对结果的影响，利用更大的计算平台考虑空间分布的多粒子的外差散斑，实验探究不同粒子大小以及粒子的数目对相干性测量的影响等。需要说明的是，这里的仿真仅作为实验参考，真实相干函数的数值还需实验测量。期待此方法可以在将要建成的上海软X-FEL用户装置以及其他的XFEL装置上得到实际应用。