随着X荧光(X-ray Fluorescence, XRF)仪性能的不断提高，其越来越广泛地被应用在低含量元素的分析中，因此对于X荧光仪检出限的研究具有重要意义。检出限由德国学者Kaiser于1947年提出后，国内外学者对其进行了大量的研究^[1-5]。2003年，梁国立等^[6]就XRF低含量元素分析的检出限问题进行了多方面的探讨，力求确定具有可比性、精确度一致的检出限，并给出了X射线荧光分析的检出限表达式。检出限受测量仪器、测量条件、测量时间与背景等多种因素的影响。对于特定的仪器，确定最佳测量条件、测量时间与合适的背景扣除方法对降低检出限值和提高对痕量元素的分析具有重要意义。2011年马晏等^[7]分析了测量时间对检出限的影响，指出测量时间对检出限有一定的影响，但其影响是有限的。本实验选取As元素为研究对象，使用分析纯的SiO₂粉末和金属As粉末，配制了浓度为100 μg·g^-1的As样品^[8]，研究了空白样本底扣除法、线性本底扣除法以及斯托林斯基法(Sterlinski)三种本底扣除法对检出限的影响，以及不同背景扣除法中管电压、管电流对X荧光仪检出限的影响。比较了三种不同背景扣除法的优劣，得到了不同背景扣除法对应的适宜管电压与管电流范围，为相关工作人员更加精准地测量低含量As及其它重金属元素提供参考。

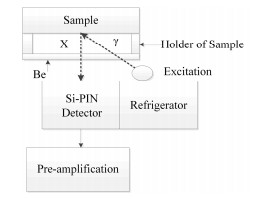
IED-2000T型手持式X荧光仪（探头部分的几何布局见图 1）：Rh靶材，最大管压为40kV；万分之一精度电子分析天平（德国Sartorius公司生产）；300目的分析纯金属As粉末与SiO₂粉末。

图 1

图 1 X荧光仪探头几何布局图 Figure 1 Geometric distribution of detector in X-ray fluorescence.

测量环境：距离探测器前0.3 m处是一面水泥墙，探测器距地面的距离为1m，地面是地板砖。

先配制含As为3000 μg·g^-1的样品500g，使用电子天平称取金属As粉末1.500g，SiO₂粉末498.500g，放入玛瑙碾钵中混合均匀。再依次称取3000 μg·g^-1的As样品3.333 g、6.667 g、10.000 g、13.333 g、16.667 g、20.000 g、33.333 g、40.000 g、66.667g加入到质量为96.667 g、93.333 g、90.000 g、89.667 g、83.333 g、80.000 g、66.667 g、60.000 g、33.333g的SiO₂粉末中，在玛瑙碾钵中混合均匀，得到As浓度分别为100 μg·g^-1、200 μg·g^-1、300 μg·g^-1、400 μg·g^-1、500 μg·g^-1、600 μg·g^-1、1000 μg·g^-1、1200 μg·g^-1、2000 μg·g^-1的样品。再称取100 μg·g^-1的As样品40.000 g加入到质量为40.000g的SiO₂粉末中，在玛瑙碾钵中混合均匀，得到As浓度为50 μg·g^-1的样品；同理配置As浓度分别为25 μg·g^-1和12.5 μg·g^-1的样品。取各浓度的样品8g以及SiO₂粉末8g（作为空白样品），置于以聚乙烯薄膜为垫底的塑料环中制样，待测。

检出限是指产生一个能可靠被检出的分析信号所需要的某元素最小含量，用于X荧光检出限的公式如下^[6]：

式中：C_L是检出限，μg·g^-1；m是灵敏度，s^-1· μg^-1·g，m=I_P/w_i，I_P是净计数率，w_i是目标元素的含量；S₀是本底标准偏差即$\sqrt{{{I}_{0}}/t}$；I₀是本底的计数率；t是测量时间，s。

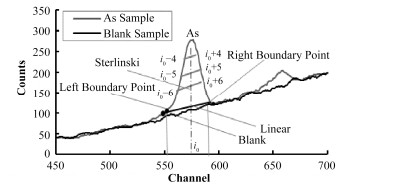
空白样扣本底法：在相同的实验条件下分别测量含As的样品与空白样，其中空白样用SiO₂粉末制备；见图 2，将空白样在左右边界内的计数作为本底计数的方法（图 2为对As含量400 μg·g^-1与空白样品测量后，运用5点算术平均法进行谱光滑处理后得到的峰谱图）。

图 2

图 2 谱光滑后的As峰谱 Figure 2 Smooth spectrum of As.

线性本底扣除法：如图 2所示将左右边界点直线连接作为本底线，本底计算表达式见式(2)。由于存在统计涨落，以左右边界点两点计算本底，误差较大。本实验将在边界点左右再各取1点，如图 2所示，将3点所对应计数的平均值作为左右边界点计数值。

式中：y_L、y_R是左、右边界点的计数；m_L、m_R是峰区左、右边界点的道址。

斯托林斯基法：在峰位两侧较光滑处选取计数值相对偏差较小的道作为边界道计算峰面积。如图 2所示，本实验在As峰位i₀左右选取离峰位4道处i₀-4、i₀+4道分别作为左右边界道，将左右边界点直线连接作为本底线，按式(2)扣本底A_{B, 1}得到净峰面积A_{P, 1}。由于边界道计数的统计涨落会严重影响峰面积的计算精度，因此在选取的左右边界道基础上分别再向左、向右扩展1道，再将i₀-5、i₀+5道分别作为左右边界道，按上述方法扣本底A_{B, 2}得到净峰面积A_{P, 2}。同上，得到A_{B, 3}、A_{P, 3}。将A_{B, 1}、A_{B, 2}、A_{B, 3}的和作为本底计数，A_{P, 1}、A_{P, 2}、A_{P, 3}的和作为净计数。

设置X荧光仪的测量时间为300s，管电压与管电流分别为32kV、16 μA，测量含As量分别为100 μg·g^-1、200 μg·g^-1、300 μg·g^-1、400 μg·g^-1、500 μg·g^-1、600 μg·g^-1、1000 μg·g^-1、1200 μg·g^-1、2000 μg·g^-1、3000 μg·g^-1的样品。分别采用空白样本底法、线性本底法、斯托林斯基法处理谱数据建立刻度曲线，使用As浓度为400 μg·g^-1的样品进行准确度分析，测量值的相对偏差如表 1所示。测量数据采用空白样本底扣除法、线性本底扣除法、斯托林斯基法处理后，其计算值与推荐值的相对偏差分别为1.84%、4.42%和4.59%，均小于5%。因此采用空白样、线性本底法、斯托林斯基法扣背景是可行的。

表 1

表 1 各方法计算值与相对偏差 Table 1 Calculated value and relative deviation of each method. 背景扣除方法 Background subtraction method 推荐值 Recommended value / μg·g-1 计算值 Calculated value / μg·g-1 相对偏差 Relative deviation / % 空白样扣本底 Blank sample deduct background 400.00 392.64 1.84 线性本底法 Linear background deduction 400.00 417.66 4.42 斯托林斯基法 Sterlinski method 400.00 418.37 4.59

表 1 各方法计算值与相对偏差 Table 1 Calculated value and relative deviation of each method.

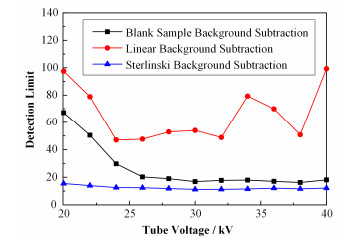
设置X荧光仪的测量时间为300s，管电流30 μA恒定，在20-40kV内不停改变管电压值，测量含As量为100 μg·g^-1的样品及空白样。分别采用上述的三种本底扣除方法处理谱数据，得到检出限值见表 2，得到检出限随管电压的变化见图 3。由图 3可知，线性本底扣除法得到的检出限随着管电压增大的变化趋势为先降低后增高；测As元素时，采用线性本底扣除法适宜的管电压范围为24-26kV。采用空白样扣本底与斯托林斯基法得到检出限随着管电压增大先降低后趋于平缓；测As元素时，采用空白样扣本底与斯托林斯基法适宜的管电压范围为28-40kV。

表 2

表 2 检出限随电压的变化 Table 2 Detection limit varies with tube voltage. 电压 Tube voltage / kV 空白样扣本底 Blank sample deduct background 线性本底法 Linear background deduction 斯托林斯基法 Sterlinski method 20 67.13 97.54 15.48 22 50.46 78.88 13.99 24 29.74 47.08 12.52 26 20.25 47.64 12.43 28 18.98 52.94 11.83 30 16.82 54.02 11.22 32 17.72 48.87 11.27 34 17.93 79.31 11.52 36 17.04 69.94 12.13 38 16.21 50.83 11.65 40 18.10 99.35 12.17

表 2 检出限随电压的变化 Table 2 Detection limit varies with tube voltage.

图 3

图 3 各方法检出限随管电压的变化 Figure 3 Change of detection limit along with the tube voltage.

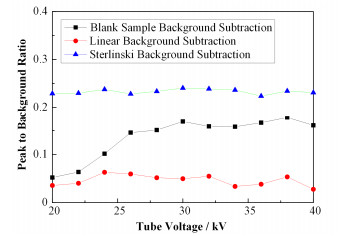
分析检出限受管电压的影响，可能是散射受管电压的影响，因此分析峰背比随管电压的变化，如图 4所示。峰背比最高的点应与检出限最低的点对应。由图 4可知，峰背比随管电压的变化与表 2刚好对应。

图 4

图 4 各方法峰背比随管电压的变化 Figure 4 Change of peak to background ratio along with tube voltage.

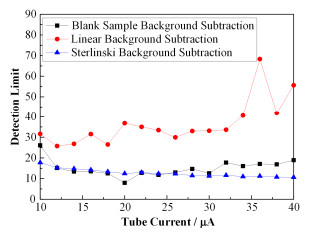
设置X荧光仪的测量时间为300s，管电压32kV恒定，在10-40 μA内不停改变管电流值，测量含As量为100 μg·g^-1的样品及空白样。分别采用上述的三种背景扣除方法处理谱数据，得到检出限值见表 3，得到的检出限随管电流的变化见图 5。由图 5可知，采用空白样扣本底与线性本底法处理谱数据得到的检出限随管电流的增大先有降低的趋势后升高；测As元素时，采用空白样扣本底适宜的管电流范围是18-24 μA，采用线性本底法适宜的管电流范围是12-14 μA。采用斯托林斯基法得到的检出限随管电流的增大而降低；测As元素时，适宜的管电流范围为18-40 μA。

表 3

表 3 各方法检出限随管电流的变化 Table 3 Detection limit varies with tube current of each method. 管电流 Tube current / μA 空白样扣本底 Blank sample deduct background 线性本底法 Linear background deduction 斯托林斯基法 Sterlinski method 10 26.07 31.62 17.76 12 15.11 25.74 15.27 14 13.41 26.78 14.78 16 13.50 31.53 14.19 18 12.50 26.50 13.33 20 7.96 36.83 12.46 22 12.77 35.04 12.96 24 11.81 33.45 12.39 26 12.99 29.94 12.33 28 14.67 33.01 11.47 30 12.57 33.14 11.27 32 17.75 33.63 11.62 34 16.04 40.65 10.99 36 17.10 68.32 11.23 38 16.89 41.82 10.77 40 18.91 55.64 10.66

表 3 各方法检出限随管电流的变化 Table 3 Detection limit varies with tube current of each method.

图 5

图 5 各方法检出限随管电流的变化 Figure 5 Change of detection limit along with tube current.

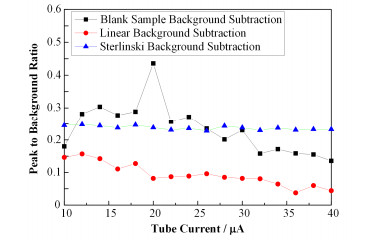
同样分析峰背比随管电流的变化，如图 6所示。由图 6和表 3可知，峰背比最高的点刚好是检出限最低的点，其随测量条件的变化与检出限的变化刚好对应，因此可以通过确定峰背比达到最高的测量条件来确定检出限测量的最佳条件。

图 6

图 6 各方法峰背比随管电流的变化 Figure 6 Change of peak to background ratio along with tube current.

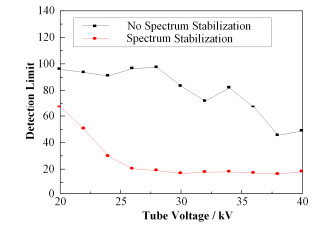
分别设置两组对比实验。将X荧光仪的测量时间设置为300s，保持管电流30 μA恒定，在20-40kV范围内改变管电压值，分析As浓度为100 μg·g^-1的样品以及空白样。其中第一组实验测量过程中不进行稳谱，测完含As样品后测空白样前不对X荧光仪重新刻度、重新寻峰使用空白样本底法对谱数据进行处理；第二组实验测量过程中进行稳谱处理，每次测空白样前都对X荧光仪重新刻度、重新寻峰。得到检出限在相同激发电流下随管电压的变化关系如图 7所示。

图 7

图 7 谱漂对检出限的影响 Figure 7 Influence of detection limit owing to the spectrum drift.

如图 7所示，在同样的实验条件下不进行稳谱，得到的检出限远高于稳谱后得到的检出限。稳谱后的检出限，在30 μA恒定激发电流下，随着激发电压的增加，其变化程度逐渐趋于平缓。由此可见，稳谱对手持XRF仪的稳定性和检出限具有重要的影响。

低含量元素的检测，不仅受到仪器噪声的限制，还受空白背景绝对水平的限制，只有当分析信号比噪声和空白背景大到一定程度时才能可靠地被分辨与检测出来。因此当元素的含量相当于检出限水平时，只能证明仪器可靠地检测出了该元素的分析信号，但不能用于定量分析。

与检出限不同，测定限(C_D)是定量分析方法实际可能测定到某元素的下限，是定量分析实际可达到的极限。元素的测定限根据检出限和分析的质量要求来确定，三者之间的对应关系^[6]见表 4。

表 4

表 4 测定限与检出限和分析误差的对应关系 Table 4 Relation between determination limit, detection limit and the range of allowable error. 分析允许误差 Range of allowable error 测定限(CD)与检出限(CL)的关系 Relation between determination limit and detection limit ±25% CD=1.333CL ±16.66% CD=2.0CL ±11.11% CD=3.0CL

表 4 测定限与检出限和分析误差的对应关系 Table 4 Relation between determination limit, detection limit and the range of allowable error.

设置管电压为32kV，管电流为20 μA，测量时间300s。将误差允许范围设定为±11.11%，采用各背景扣除方法得到的检出限与测定限见表 5。

表 5

表 5 测定限含量 Table 5 Content of determination limit. 背景扣除方法 Background subtraction method 空白样扣本底 Blank sample deduct background 线性本底法 Linear background deduction 斯托林斯基法 Sterlinski method 检出限 Detection limit 7.96 36.83 12.46 测定限 Determination limit 23.88 110.49 37.38 取整 Rounding 25 110 40

表 5 测定限含量 Table 5 Content of determination limit.

由表 5可知，利用空白样扣本底得到的测定限含量最低，约为25 μg·g^-1。建立背景扣除方法下的工作曲线，分析25 μg·g^-1的样品，所得结果见表 6。

表 6

表 6 利用刻度曲线测25 μg·g-1含As样品所得结果 Table 6 Results of the content of As 25 μg·g-1 sample by calibrating curve. 背景扣除方法 Background subtraction method 推荐值 Recommended value 计算值 Calculated value 相对偏差 Relative deviation / % 空白样扣本底 Blank sample deduct background 25.00 27.14 8.57 线性本底法 Linear background deduction 25.00 38.16 52.65 斯托林斯基法 Sterlinski method 25.00 29.39 17.54

表 6 利用刻度曲线测25 μg·g-1含As样品所得结果 Table 6 Results of the content of As 25 μg·g-1 sample by calibrating curve.

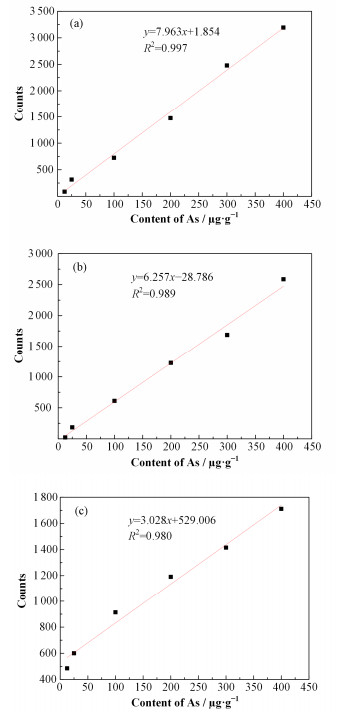
由表 5可知，在±11.11%误差范围内，空白样扣本底法的测定限含量约25 μg·g^-1，线性本底法的测定限含量约110 μg·g^-1，斯托林斯基法的测定限含量约40 μg·g^-1。由表 6可知，利用空白样扣本底所得结果的相对标准偏差为8.57%；在误差允许的范围内，利用线性本底法所得结果的相对偏差远超出了误差允许的范围，然后测量了110 μg·g^-1，所得结果相对误差为4.43%；利用斯托林斯基法所得结果也高出了误差允许的范围，然后测量了40 μg·g^-1，所得结果相对误差为4.11%。验证了元素的含量高于测定限含量时，方可得到较为可靠的结果。因此可通过检出限得到测定限对低含量元素的定量分析。空白样本底扣除法、线性本底扣除法及斯托林斯基法分析As的刻度曲线如图 8所示。

图 8

图 8 空白样本底扣除法(a)、线性本底扣除法(b)及斯托林斯基法(c)分析As的刻度曲线 Figure 8 Calibration cure of the As by the blank sample deduction method (a), linear background deduction method (b) and As by Sterlinski method (c).

采用线性本底法获得的检出限随管电压与管电流的变化较大；采用斯托林斯基法得到的检出限随管电流的增大趋于平稳。线性本底扣除法属于全峰法，斯托林斯基法属于半峰法，因此可知峰边界处对管电压与管电流的变化反应最为敏感，使用全峰法适宜的管电压与管电流范围较小，因而使用全峰法处理谱数据时应严格设置管电压与管电流在适宜的范围内。

本底谱的形成除受仪器噪声的影响外，由于散射和谱线重叠干扰，还受周围材料的散射、样品基体和所要测量的元素等因素的影响。但仪器的稳定性较好时，采用空白样品本底可以反映出周围材料散射和样品基体的干扰因素，此方法受仪器稳定性的影响较大；斯托林斯基法主要反映的是峰区的情况，本底对峰区的影响相对较小，因此采用斯托林斯基法便减弱了本底对元素测量的影响，因此斯托林斯基法随管电压与管电流的变化也较为平稳。斯托林斯基法属于半峰分析方法，并不能反映真实的本底情况，在测量真实本底时不适用此方法。

使用Rh靶便携式能量色散型X荧光仪测量As元素时，检出限随管电压与管电流的变化因背景扣除方法的不同呈现不同的趋势。测As时，采用空白样扣本底适宜管电压范围是28-40kV；适宜管电流范围是18-24 μA。线性本底法扣本底适宜管电压范围是24-26kV；最佳管电流范围是12-14 μA。采用斯托林斯基法适宜管电压范围是28-40kV；适宜管电流范围18-40 μA。三种背景扣除方法中空白样扣本底为最佳的本底扣除方法，斯托林斯基法次之，低含量元素分析中不适宜使用线性本底法扣本底。在对于低含量目标元素的谱数据处理，采用半峰法优于全峰法。峰背比随测量条件的变化刚好与检出限对应，可以通过确定峰背比达到最高的测量条件来确定检出限测量的最佳条件。本文所采用的方法可用于对其它重金属元素的分析。