2. 中国科学院大学 北京 100049;
3. 上海科技大学 上海 201800
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. ShanghaiTech University, Shanghai 201800, China
钍基熔盐堆核能系统(Thorium-based Molten Salt Reactor, TMSR)是中国科学院先导科技专项之一,以研发第四代裂变反应堆核能系统为其战略目标[1]。10MW热功率固态燃料钍基熔盐实验堆(The Solid Fuel Thorium-Based Molten Salt Experimental Reactor, TMSR-SF1) 是一个熔盐冷却球床堆,采用传统的三结构同向性型(Tri-structural Iso-tropic, TRISO)包覆颗粒燃料,低压高温熔盐作为冷却剂[2]。TMSR-SF1功率控制系统是反应堆一个关键控制系统。它采用手动操作或自动调节方式,通过改变控制棒的位置来调节或维持反应堆功率。此外,功率调节系统需与核测系统、反应堆保护系统、棒位测量与指示系统,以及其他控制、调节系统相互作用、联锁,是一逻辑较复杂、规模较庞大的系统。反应堆功率控制系统的主要设计要求就是在反应堆正常运行条件下,实现反应堆功率自动跟随负载变化,并且其超调量、响应时间、稳态误差等各动态性能指标应满足安全运行的要求[3-4]。同时,反应堆在运行过程中会受到不确定性因素的影响,如在不同的运行功率下导致系统模型参数发生变化等[5-6]。这些不确定性因素的影响都可能导致功率控制系统的控制性能变差。因此,反应堆功率控制系统除了具备良好的动态性能外,还应具有良好的抗干扰能力,以保证反应堆在运行过程中始终是稳定可靠的。
为了满足上述的设计要求,大量研究人员采用不同的控制方法设计反应堆的功率控制系统。如文献[7]采用三回路比例、积分、微分(Proportional Integral Derivative, PID)控制方法,与传统PID控制相比,其控制效果有了显著的提高。文献[8]采用自适应反馈控制方法控制堆芯输出功率,取得了很好的控制效果。文献[9]在堆芯功率跟随负载的控制系统中采用自适应模糊控制方法,其仿真结果表明所设计的控制系统比经典的控制系统更稳定、响应速度更快、鲁棒性更强。
由于反应堆在运行过程中受到的不确定性因素的影响(如在不同运行功率下模型参数的变化),会使得功率控制系统的性能变差。而自适应控制能根据系统的动态特性实时改变控制参数,控制精度高,确保控制系统在受到不确定性因素影响时能快速调整控制参数,使控制系统保持在最优工作状态下。因此,本文采用模型参考自适应控制算法来设计反应堆功率控制系统。根据文献[10]中的自适应控制理论与稳定性定理,设计固态燃料熔盐堆的自适应功率控制器,并分析其控制特性,以确保TMSR-SF1堆芯的输出功率跟随负载实时变化。
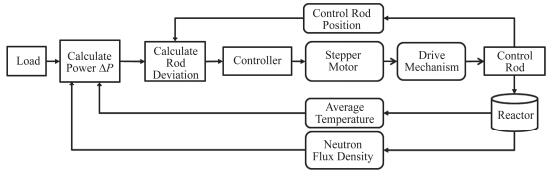
1 反应堆功率控制系统 1.1 一般堆功率控制系统反应堆功率控制系统主要包括信号测量单元和控制执行单元[11]。信号测量单元主要包括堆芯输出功率水平测量设备、堆芯进(出)口温度测量设备和步进电机转速测量设备,能够实时地监测反应堆的工作状态,并将检测到的反馈信号输入到控制器。控制执行单元包括输入输出接口、步进电机、减速器和控制棒驱动机构,其直接调节控制棒的棒位,间接达到调节堆芯功率的目的。反应堆控制系统框图如图 1所示。
|
图 1 堆功率控制系统框图 Figure 1 Block diagram of reactor power control system. |
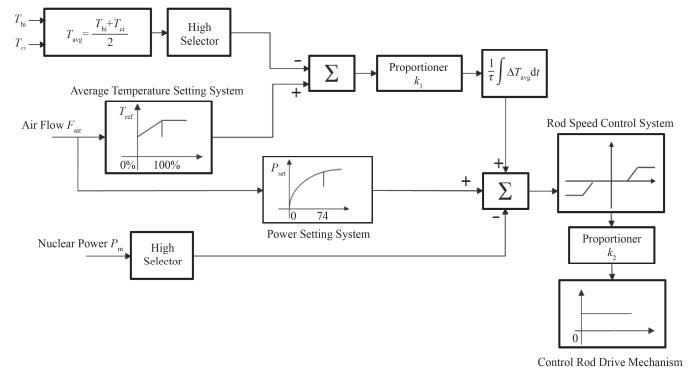
TMSR-SF1功率控制方案如图 2所示[12]。图 2中符号∑表示的是求和,符号∫表示的是对信号进行积分运算。TMSR-SF1是一个固态燃料熔盐实验堆,堆芯核热功率通过一回路换热器转移到二回路,再通过二回路散热器将热量排到大气中。通过调节散热器的空气流量来调节空气带走的热功率,也即可以将调节空气流量当作是负载功率调节方式。其控制流程如下:
|
图 2 TMSR-SF1功率控制系统框图 Figure 2 Block diagram of TMSR-SF1 power control system. |
1) 将过程测量系统来的若干组反应堆入口温度信号、出口温度信号分别送入控制系统信号甄别器;
2) 经甄别器后反应堆入口温度和出口温度作为平均温度计算单元的输入量;
3) 平均温度计算单元利用甄别器送出的入口温度和出口温度计算一回路熔盐平均温度;
4) 各组平均温度经高选单元产生高选平均温度作为反应堆一回路熔盐平均温度Tavg;
5) 将经过滤波后的反应堆一回路熔盐平均温度Tavg与相应工况下的参考平均温度Tref比较,产生平均温度偏差信号ΔTavg=Tref−Tavg;
6) ΔTavg经比例积分环节处理转换成归一化的热功率参数ΔPT;
7) 从核测量系统送来三路功率信号,经高选单元产生高选核功率信号(实测功率信号)Pm;
8) ΔPT参数与总空气流量经比例器转换为归一化的外负荷参数及归一化的核功率参数三者求代数和;
9) 将功率偏差信号ΔP送入棒速程序单元,产生控制棒移动速度和移动方向信号,棒速信号经过转换单元处理转换成开关量信号,再将棒速和棒方向信号送入棒控系统,驱动控制棒移动,改变堆芯反应性,调节反应堆功率,从而达到功率控制的目的。
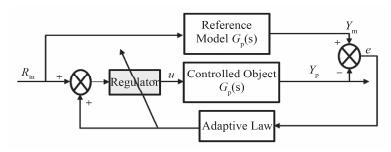
2 自适应功率控制器设计 2.1 自适应控制系统核反应堆在正常运行过程中,由于在不同的功率水平下,系统模型的参数会改变,致使控制特性变差。为了保证反应堆的正常运行,本文采用参考模型自适应控制算法,设计TMSR-SF1的功率控制系统。目前比较常见的参考模型自适应控制系统设计方法有两种,分别是:基于局部参数最优化理论为基础的设计方法(MIT方法)和基于Lyapunov稳定性理论的设计方法。一个合适可行的模型参考自适应控制系统首先应当是全局稳定的。基于MIT律的模型参考自适应控制系统往往很难保证稳定。为了解决这个问题,利用稳定性理论来设计模型参考自适应控制系统的方法被提出。该方法与局部参数优化方法相比不仅可以保证设计出的系统的全局稳定性,还有调节过程用时较短的优点。因此,本文采用基于Lyapunov稳定性理论的设计方法。模型参考自适应控制结构框图如图 3所示。
|
图 3 模型参考自适应控制器结构框图 Figure 3 Structure of model reference adaptive controller. |
图 3中符号⊗表示的是加减运算,符号
在反应堆跟随负载稳定运行时,负载保持不变,根据平均温度设定系统计算出的平均温度设定值为一定值,而堆芯平均温度是一个动态值,故堆芯平均温度与设定值的偏差ΔTavg是动态误差,这会导致补偿功率的波动。若波动过大会引起功率控制系统的波动,不利于堆芯输出功率的控制。为了稳定平均温度偏差ΔTavg的波动,引入一个单输入单输出的二阶调节系统,其调节系统的模型描述为:
| $\frac{{{Y}_{\text{p}}}\left( s \right)}{U\left( s \right)}={{G}_{\text{p}}}\left( s \right)={{k}_{\text{p}}}\cdot \frac{as+b}{{{s}^{2}}+cs+d}$ | (1) |
式中:kp为缓时变参数;a、b、c、d均大于0。根据图 3所示,需要根据温度偏差-功率补偿的特性和偏差控制要求设计参考模型。由式(1) 可知,设计的参考模型如式(2) 所示。
| $\frac{{{Y}_{\text{m}}}\left( s \right)}{{{R}_{\text{in}}}\left( s \right)}={{G}_{\text{m}}}\left( s \right)={{k}_{\text{m}}}\cdot \frac{\alpha s+\beta }{{{s}^{2}}+\xi s+\omega }$ | (2) |
根据可调增益模型参考自适应控制的设计原理,故有α=a、β=b、ξ=c、ω=d,且当被控对象追踪到参考模型时,应满足km=kckp,其中kc为可调的控制增益。因此,设计参考模型的km就显得尤其重要。对于被控对象中的参数,为了降低调节过程中的超调量和缩短系统的响应时间,经过反复计算得出a=1、b=10、c=18、d=100,则根据输入与理想输出的关系,可以得到理想km值为10。然后根据关系式km=kckp来设计自适应增益调节律。
将传递函数转化为状态空间可观测型为:
| $\begin{align} &\dot{x}=Ax+Bu \\ &y=Cx+Du \\ \end{align}$ | (3) |
式中:A为系统矩阵,表示系统内部各状态变量的关系;B为控制矩阵,表示输入信号对状态变量的影响;C为输出矩阵,表示状态变量与输出信号的关系;D为直联矩阵,表示输入信号对输出信号的影响;x为状态向量;u为输入向量;y为输出向量;
此时,状态空间各矩阵为:
| $A=\left[ \begin{matrix} -18&-100 \\ 1&0 \\ \end{matrix} \right],\ B=\left[ \begin{matrix} 1 \\ 0 \\ \end{matrix} \right],\ C=\left[ \begin{matrix} 1&10 \\ \end{matrix} \right],\ D=0$ | (4) |
根据Lyapunov稳定性理论寻求可调增益的调节规律,使参考模型输出与系统实际输出的广义误差e趋于0。由自适应模型结构框图 3可得广义误差为:
| $e={{Y}_{m}}-{{Y}_{p}}$ | (5) |
根据Lyapunov稳定性定理可知,构造一个Lyapunov函数为:
| $V=\gamma {{x}^{T}}Px+{{k}^{2}}$ | (6) |
式中:γ > 0,为常量;k=km−kpkc;xT表示对x向量进行转置运算;P为对称正定矩阵,且满足ATP+PA=−Q(Q为正定对称矩阵)。故V是正定函数。对V进行求导化简计算得:
| $\dot{V}=\gamma {{x}^{T}}Qx+2\gamma u{{B}^{T}}Px+2k\dot{k}$ | (7) |
因u=kRin(Rin为控制器的输入信号),代入到式(7) 中得到:
| $\dot{V}=\gamma {{x}^{T}}Qx+2k\left( \gamma {{R}_{\text{in}}}{{B}^{T}}Px+\dot{k} \right)$ | (8) |
若令
| $\dot{k}=\gamma {{R}_{\text{in}}}{{B}^{T}}Px$ | (9) |
因k=km−kpkc,而kp变化相对于kc变化可以近似忽略不计,则可以得到自适应律为:
| ${{\dot{k}}_{\text{c}}}\approx \dot{k}=\gamma {{R}_{\text{in}}}{{B}^{T}}Px$ | (10) |
因传递函数为严格正实函数,有C=BTP,根据关系式可以求出P和Q皆为正定对称矩阵:
| $p=\left[ \begin{matrix} 1&10 \\ 10&120 \\ \end{matrix} \right],\ Q=\left[ \begin{matrix} 16&160 \\ 160&2\,000 \\ \end{matrix} \right]$ | (11) |
并代入到式(10) 中,则简化得到:
| ${{\dot{k}}_{\text{c}}}=\gamma {{R}_{\text{in}}}e$ | (12) |
即式(12) 为控制器设计的自适应增益调节律。
故设计的自适应增益调节律能保证系统是全局渐近稳定的,自适应控制系统也是全局渐近稳定的系统。
2.3 自适应增益律的Simulink实现根据式(12) 可知,自适应增益调整律与自适应增益γ、控制器输入Rin和广义误差e相关,故在Simulink中实现自适应增益调整律如图 4所示。

|
图 4 自适应律的Simulink实现 Figure 4 Simulink implementation of adaptive law. |
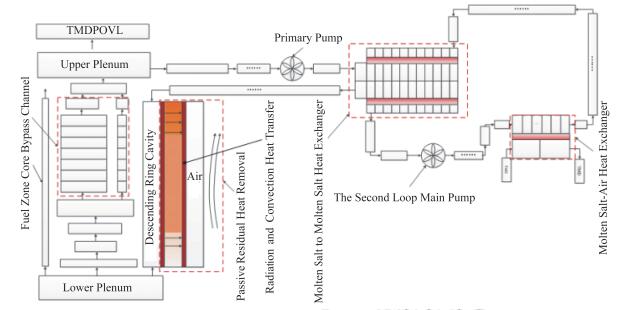
TMSR仿真平台是一个基于EPICS (Experimental Physics and Industrial Control System)[13-14]架构的实时运行控制仿真平台,其包括:EPICS实时数据库、控制与保护逻辑、系统分析程序、三维中子动力学、人机界面、教控台、关系数据库和管理配置等程序模块。各个功能模块通过EPICS通道访问协议(CA协议),使用EPICS实时数据库进行数据交互。TMSR仿真平台的系统结构图见图 5。本文使用实时版本RELAP5系统程序建模TMSR-SF1实验堆系统[15],其系统模型如图 6所示。采用MATLAB/Simulink作为控制与保护逻辑建模工具建立模型参考自适应功率控制模型,如图 7所示。

|
图 5 TMSR仿真平台系统结构图 Figure 5 Block diagram of TMSR simulation platform. |
|
图 6 反应堆系统模型 Figure 6 Schematic diagram of the reactor system model. |

|
图 7 模型参考自适应功率控制模型 Figure 7 Model reference adaptive power control model. |
首先,通过研究不同自适应增益γ对控制系统的影响,以获得合适的自适应增益γ值。在选定合适γ值的情况下,分析自适应过程中自适应率的调节规律、自适应追踪效果以及负载跟随特性。为验证控制器的抗干扰能力,引入不确定性干扰信号进行抗干扰分析。
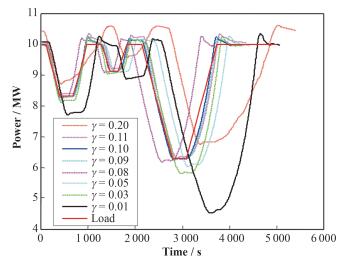
3.2.1 自适应增益γ对控制器的影响对于不同的自适应增益γ,自适应控制器的性能也会有所不同,对功率跟随负载的控制性能影响也各有差异。当自适应增益γ取值过大(小)时,根据式(12) 可知,自适应率也会相应的过大(小),导致自适应过程波动。对于动态系统而言,控制系统的波动会导致整个系统的超调量增大、响应迟滞。如图 8(横坐标表示运行时间,纵坐标表示功率值)所示,当γ取值大于0.11(为0.2)时,控制系统的超调量偏大,响应延迟大,不能保证堆芯功率跟随负载运行;当γ取值小于0.03(为0.01)时,控制系统的负载跟随能力变差,超调量偏大(功率从100%下降到60%左右),响应延迟大。当取值在0.03−0.2之间时,其负载跟随控制超调量小,响应速度快,有利于堆芯功率负荷跟随的控制和提升控制系统的可靠性。通过分析比较,当γ值为0.11或0.09(0.08)时,控制系统的超调量会增大,响应时间会延长(相对于γ=0.1时)。因此,选取合适的γ值为0.1,并对控制器的其它特性进行分析研究。
|
图 8 不同自适应增益的控制效果对比 Figure 8 Comparison of control effects of different adaptive gains. |
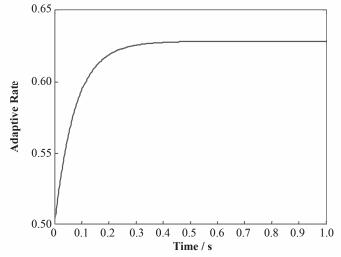
堆芯功率控制系统运行时,由式(12) 可知,自适应控制器的自适应调整率
|
图 9 自适应率的调节规律 Figure 9 Regulation of adaptive rate. |

|
图 10 自适应追踪效果 Figure 10 Effectiveness of adaptive tracking. |
根据选取的γ值,进行控制器负载跟随的特性分析。假定负载以5%·min−1的速率按照100%-50%-100%变化[16],堆芯功率的变化如图 11所示。在没有控制器时,堆功率跟随负载运行效果不是很理想,功率下降到50%满功率(Full Power, FP)时,超调量较大,功率误差也大;负载从50% FP上升到100% FP时,功率在开始上升时,偏离负载的误差较大,达到2%左右,跟随控制不理想;达到100% FP时,堆芯功率与负载误差较大,有1%左右。加入自适应控制器后,到达50% FP时,超调量较小,与设定功率的误差小;负载从50%-100% FP时,堆芯功率在负载开始变化时,会偏离一点,误差在1%左右;达到100% FP时,堆芯功率与负载几乎没有偏差。因此,对于γ取值为0.1的自适应控制器可以保证TMSR-SF1的堆芯功率跟随负载运行,说明了所设计的自适应控制系统是可靠的。

|
图 11 100%-50%-100%负载功率以5%·min−1的速率变化时的堆芯功率变化 Figure 11 Changes of reactor core power vs. 100%-50%-100% ramp load with 5%·min−1 rate. |
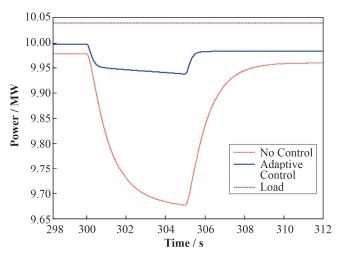
堆芯输出功率跟随负荷稳定运行过程中,由于干扰信号的影响,导致控制棒驱动系统产生误动作,促使堆芯功率发生改变。功率控制系统迅速响应,调节控制棒,吸收掉干扰信号,保证堆芯功率跟随负载运行,如图 12所示。控制棒误动作下插后,在没有自适应控制器时,堆芯功率迅速下降,功率控制系统根据功率偏差信号,输出控制棒驱动信号调节控制棒上提,使堆芯热功率降到9.675MW后,功率再迅速上升到9.95MW,随后渐渐达到稳定运行状态。在有自适应控制器的情况下,堆芯功率在下降到与负载偏差超过0.1MW时,控制系统迅速响应,促使控制棒驱动机构调节控制棒,堆芯功率缓慢下降,再调整堆芯功率跟随负载功率运行,偏差值在0.1MW范围内。因此,这说明了自适应控制系统具有较强的抗干扰能力。在控制系统受到干扰信号影响时,控制回路能迅速将其吸收掉,保证了反应堆的正常运行。
|
图 12 自适应控制系统抗干扰特性 Figure 12 Anti interference characteristics of adaptive control system. |
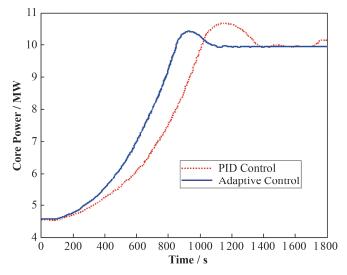
堆芯功率从低功率运行条件(45% FP)下攀升到满负荷运行时,在经典PID控制器的情况下,堆芯功率在100s附近开始攀升,在1150 s时达到10.7MW后再下降至10MW附近波动并最终稳定在10MW运行;而在自适应控制器情形下,功率在100s处开始攀升,在900s攀升到10.35MW后开始下降至10MW稳定运行,几乎没有功率波动,见图 13。表明了自适应控制器比PID控制器的响应速度快,超调量更小,稳定性更高,大大提升了功率控制系统的性能。
|
图 13 自适应与PID功率攀升控制对比 Figure 13 Comparison of adaptive and PID control when the power is climbing up. |
依据TMSR-SF1实验堆功率控制的要求,结合模型参考自适应控制理论,设计固态燃料熔盐堆功率自适应控制器。采用Lyapunov稳定性理论对控制器的自适应律进行设计,根据定理设计的自适应调节律可以保证自适应功率控制系统是全局渐近稳定的。并基于TMSR仿真平台,使用MATLAB/ Simulink模块建立自适应功率控制系统模型,开展控制器特性分析。分析了自适应增益γ对自适应控制器的性能影响,模拟结果表明自适应参数过大或者太小不利于控制性能的提升,并获得合适的自适应增益γ=0.1。基于确定的γ参数值,分析了控制器自适应率的调节规律,以及被控对象追踪参考模型的控制效果,验证了自适应控制器在全局渐近稳定和具有可靠的控制性能。反应堆功率跟随负荷的模拟分析,进一步验证了自适应控制器控制堆芯功率跟随负荷变化的稳定性和可靠性。在系统存在干扰噪声的情况下,分析控制系统的抗干扰能力,结果表明自适应控制系统能快速响应,吸收掉这些噪声,控制器具有很强的抗干扰能力。与经典PID控制进行对比,表明自适应控制比PID控制响应速度更快,超调量更小,更有利于控制系统的稳定。因此,所设计的模型参考自适应功率控制器是稳定和可靠的,具有很强的抗干扰能力,满足TMSR-SF1功率负载跟随控制的要求。
| [1] |
江绵恒, 徐洪杰, 戴志敏. 未来先进核裂变能——TMSR核能系统[J].
中国科学院院刊, 2012, 27(3): 366–374.
JIANG Mianheng, XU Hongjie, DAI Zhimin. Advanced fission energy program-TMSR nuclear energy system[J]. Bulletin of Chinese Academy of Sciences, 2012, 27(3): 366–374. DOI: 10.3969/j.issn.1000-3045.2012.03.016 |
| [2] |
TMSR卓越中心. 10 MWth固态燃料钍基熔盐实验堆概念设计报告[R]. 上海: 中国科学院上海应用物理研究所, 2014.
TMSR Research Center. The conceptual design report 10 MWth solid thorium-based molten salt experiment reactor[R]. Shanghai:Shanghai Institute of Applied Physics, Chinese Academy of Sciences, 2014. |
| [3] |
郭胤, 黄晓津. 反应堆功率保成本控制器设计[J].
核科学与工程, 2009, 29(2): 118–122.
GUO Yin, HUANG Xiaojin. Design of nuclear reactor power guaranteed cost controller[J]. Chinese Journal of Nuclear Science and Engineering, 2009, 29(2): 118–122. DOI: 10.3321/j.issn:0258-0918.2009.02.004 |
| [4] |
杜晓光, 张君, 关济实. 软件仿真核电站堆芯核测量系统的设计与实现[J].
核技术, 2012, 35(2): 151–155.
DU Xiaoguang, ZHANG Jun, GUAN Jishi. Development of a simulation system for designing in-core neutron flux measurement in an NPP[J]. Nuclear Techniques, 2012, 35(2): 151–155. |
| [5] |
李琦, 杜建勇, 柳琳琳, 等. AP1000主控室设备抗震鉴定试验研究[J].
核技术, 2013, 36(4): 69–72.
LI Qi, DU Jianyong, LIU Linlin, et al. Experimental study on seismic qualification test of AP1000 main control room equipment[J]. Nuclear Techniques, 2013, 36(4): 69–72. |
| [6] |
程懋松, 戴志敏. 熔盐增殖堆初步安全分析[J].
核技术, 2013, 36(6): 060601.
CHENG Maosong, DAI Zhimin. Preliminary safety analysis of molten salt breeder reactor[J]. Nuclear Techniques, 2013, 36(6): 060601. DOI: 10.11889/j.0253-3219.2013.hjs.36.060601 |
| [7] |
朱昊, 韦钢, 翟春荣. 核电站堆功率调节器的设计与改进[J].
核技术, 2013, 36(12): 120605.
ZHU Hao, WEI Gang, ZHAI Chunrong. Design and improvement of nuclear power plant reactor power controller[J]. Nuclear Techniques, 2013, 36(12): 120605. DOI: 10.11889/j.0253-3219.2013.hjs.36.120605 |
| [8] | Zhe D. Adaptive output-feedback power-level control for modular high temperature gas-cooled reactors[J]. Chinese Journal of Chemical Engineering, 2015, 23(12): 2092–2097. DOI: 10.1016/j.cjche.2015.08.027 |
| [9] | Rojas-Ramírez E, Benítez-Read J S, Ríos S D L. A stable adaptive fuzzy control scheme for tracking an optimal power profile in a research nuclear reactor[J]. Annals of Nuclear Energy, 2013, 58(8): 238–245. DOI: 10.1016/j.anucene.2013.03.026 |
| [10] |
庞中华, 崔红.
系统辨识与自适应控制MATLAB仿真[M]. 北京: 北京航空航天大学出版社, 2009.
PANG Zhonghua, CUI Hong. System identification and adaptive control MATLAB simulation[M]. Beijing: Beihang University Press, 2009. |
| [11] |
汪全全, 尹聪聪, 孙雪静, 等. TMSR核功率控制系统的PID设计与仿真[J].
核技术, 2015, 38(2): 020601.
WANG Quanquan, YIN Congcong, SUN Xuejing, et al. PID design and simulation of TMSR nuclear power control system[J]. Nuclear Techniques, 2015, 38(2): 020601. DOI: 10.11889/j.0253-3219.2015.hjs.38.020601 |
| [12] |
程懋松. 反应堆功率控制系统设计说明书[R]. 上海: 中国科学院上海应用物理研究所, 2015.
CHENG Maosong. Manual of reactor power control system[R]. Shanghai:Shanghai Institute of Applied Physics, Chinese Academy of Sciences, 2015. |
| [13] | EPICS home page[EB/OL]. 2014-7-9. http://www.aps.anl.gov/epics. http://www.aps.anl.gov/epics/base/R3-15/0-docs/AppDevGuide.pdf |
| [14] | Kraimer M R, Anderson J B, Johnson A N, et al. EPICS application developer's guide[EB/OL]. 2014-12-5. http://www.Aps.anl.gov/epics/base/R3-14/12.php. |
| [15] |
王凯, 施承斌, 程懋松. TMSR-SF1工程仿真机系统建模说明书[R]. 上海: 中国科学院上海应用物理研究所, 2016.
WANG Kai, SHI Chengbin, CHENG Maosong. Manual of TMSR-SF1 engineering simulator system modeling[R]. Shanghai:Shanghai Institute of Applied Physics, Chinese Academy of Sciences, 2016. |
| [16] | Khorramabadi S S, Boroushaki M, Lucas C. Emotional learning based intelligent controller for a PWR nuclear reactor core during load following operation[J]. Annals of Nuclear Energy, 2008, 35(11): 2051–2058. DOI: 10.1016/j.anucene.2008.05.014 |


