2. 中国科学院大学 北京 100049;
3. Advanced Photon Source, Argonne National Laboratory, Argonne, IL 60439, USA
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Advanced Photon Source, Argonne National Laboratory, Argonne, IL 60439, USA
由于硬X射线微米、纳米探针具有高能量、高穿透能力、高探测灵敏度、高空间分辨率等特点,因此被广泛应用于众多学科领域的研究探索中。为了追求更好的空间分辨率、更高的通量,科学家们在一个多世纪里发展出了一系列的聚焦方法和技术,如基于折射方法的复合折射透镜CRLs[1]、Kino透镜[2-3]、AFLs透镜[4];基于反射方法的波导[5-6]、毛细管、非球面反射镜[7-8];基于衍射方法的波带片[9-11]、多层膜劳厄透镜[12-14]等。
在众多聚焦方法和技术中,采用动态压弯的非球面弹性压弯镜系统由于具有聚焦效率高、空间分辨率高、加工难度较低、光学参数可调、消色散等特点而被广泛应用。目前国际上已经发展了一系列弹性压弯的方法和技术,其中欧洲同步辐射光源(European Synchrotron Radiation Facility, ESRF)已经实现了小于50nm的聚焦光斑[15]。国内也进行了弹性压弯机理的研究和相关技术的研制,并取得了一系列的结果。作为国内第一条实现硬X射线微米和亚微米聚焦的探针线站,上海光源硬X射线微聚焦及应用线站采用压弯K-B镜实现了小于2μm的聚焦光斑[16]。在压弯机理方面,我们提出了没有任何近似的几何精确压弯理论[17]。根据实际情况,提出复杂姿态下通过调节宽度方式补偿重力的方法[18]。在此基础上并针对上海光源硬X射线微聚焦线站的光束线条件,与美国阿贡国家实验室APS (Advanced Photon Source)合作研制了基于Weak-Link[19]的柔性铰链压弯机构。
非球面压弯聚焦镜系统主要由镜体、压弯机构构成。与硬X射线微米尺度的聚焦相比,纳米聚焦对镜子面形的要求更为苛刻,如本文的光学参数设计中水平方向聚焦镜的面形误差要求小于0.5μrad。因此压弯镜的设计需要考虑以下因素:非球面形压弯的精确计算与分析;根据设计指标,选择合理的镜体物理参数;分析和设计高精度的压弯机构;误差的分析与控制。
1 压弯镜和压弯机构的设计硬X射线亚微米聚焦压弯镜系统主要由镜体和压弯机构组成,其光学参数设计主要基于上海光源硬X射线微聚焦线站BL15U1的束线条件。BL15U1线站采用了一块超环面镜用于对垂直方向准直、水平方向聚焦。因此垂直方向为平行光,压弯镜的理想面形为抛物面;水平方向为次级点光源,次级光源点光斑尺寸由狭缝控制(本文采用10μm),压弯镜的理想面形为椭圆柱面。由于BL15U1线站主要开展微米探针实验且并未针对纳米聚焦优化,因此本工作中设计的非球面压弯镜的理论聚焦光斑尺寸为亚微米级别。上海光源二期纳米探针线站建成以后,可开展聚焦光斑尺寸小于50nm的非球面压弯镜的设计。
压弯机构和镜体的设计和分析采用了几何精确压弯理论[17]。传统压弯理论,为了简化计算采用了较多近似。考虑压弯镜实际工作情况:镜子具有一定厚度;工作面为压弯过程中被压缩的非球面表面;镜子的设计和加工采用的是稳定的镜中心面;镜体被压弯后,镜面和镜中心面由平面变成曲面,空间坐标系发生了变化。传统理论并没有区分这些情况并做了简化近似处理,会在计算和设计中引入初始误差,之前的分析结果[17]表明会在局域(如镜两端)产生从几百纳弧度到几个微弧度的面形误差。为了分析和消除传统理论产生的误差,我们采用了几何精确压弯理论:用严格解析的非球面方程,替代传统理论中泰勒级数展开并截断到有限阶数的多项式方程;采用三个笛卡尔坐标系、二个弧长坐标系及多重坐标系之间的相互转化,解决了镜体压弯前后空间变化的问题;采用考虑厚度的严格曲率方程,替代传统理论中面形的二阶导数表示方式;结合压弯非球面镜设计和分析的特点,推导了压弯半径与面形误差之间的关系,可精确分析误差并有利于优化改进设计。
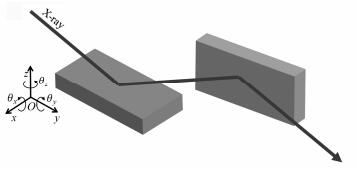
1.1 镜体参数的设计为了对水平和垂直两个方向聚焦,采用互相垂直的两块镜子即K-B镜分别对两个方向聚焦,如图 1所示。对于光源点尺寸、发散度在水平方向与垂直方向存在较大差异的同步辐射光源来说,K-B镜保留了两个方向参数设计的自由度,可以对光通量等指标进行必要的优化。两块镜子相互垂直的精度要求较高,以避免镜子面形的相互耦合影响聚焦效果。
|
图 1 聚焦K-B镜布局图 Figure 1 Schematic of K-B focusing mirrors. |
为了能对两个方向进行聚焦,采用一前一后且相互垂直的K-B镜模式。水平和垂直方向聚焦的压弯镜,设计和分析基本一致。由于经费的局限,本文目前完成了水平聚焦压弯镜的研制,因此主要讨论了水平方向聚焦镜。水平聚焦镜参数为:掠入射角3mrad,镜体长度9cm,镜体工作长度大于等于4cm,镜体面形为椭圆面形,源距600cm,像距8cm,10keV下衍射极限分辨率约100nm。
光学参数配置需要与光束线条件匹配,并由此确定空间分辨率的设计。上海光源硬X射线微聚焦光束线的水平方向为点光源,因此水平方向聚焦镜为椭圆面镜。受限于光束线条件,设计的压弯镜理论聚焦光斑尺寸为亚微米级别。
K-B镜尺寸和材质的选择,需要在镜体刚度与电机驱动力之间平衡。保证镜体足够的刚度以避免扭曲和拉伸的同时,需要电机有足够的驱动力压弯镜体。我们拟采用美国NEWPORT公司的电机Picomotor 8301可提供的最大驱动力为22N,根据电机特性为了保持稳定有效实际最大驱动力按减半处理,因此结合力臂长度压弯力矩需要控制在1N·m以内。
水平方向的椭圆面聚焦镜的宽度为25mm、厚度5.5mm、材料为单晶硅。在几何精确压弯理论[17]中,镜体的宽度分布为:
| $b(s) = \frac{{{b_0}{\rho _{\rm{c}}}(s)M(s)}}{{E{I_0}}}$ | (1) |
式中:ρc为用s坐标系描述的镜中轴面曲率方程;b0为镜中心的宽度;E为镜体材料的杨氏模量;I0为镜中心截面的惯性矩;M(s)为镜体在压弯情况下长度方向的力矩分布。
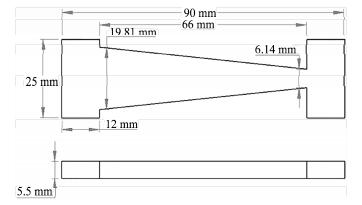
由于采用等力矩压弯模式,因此镜体的宽度变化与压弯后镜表面的曲率半径成正比关系,采用前文所述的光学参数,根据几何精确压弯理论[17],镜体设计如图 2所示。
|
图 2 镜体工程图 Figure 2 Engineering drawing of bent mirror. |
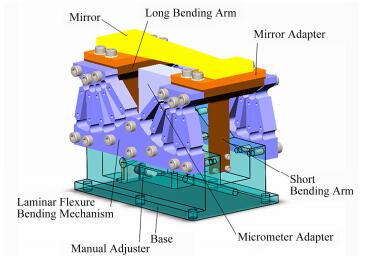
针对研究要求,与APS合作设计了一套微型动态压弯机构(图 3)。机构包括基底、一对层状柔性铰链机构、一个压电电机、长压弯力臂、短压弯力臂以及手动调节装置。
|
图 3 微型动态压弯机构的三维模型图 Figure 3 Three dimension model of the miniature dynamic mirror bender. |
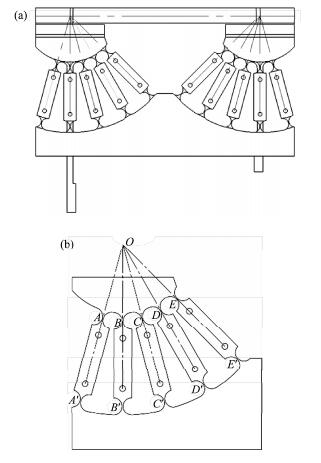
作为弹性压弯实现非球面形的动力学压弯装置,压弯机构及姿态调节是机械设计的关键部分。为了实现微米、亚微米X射线光斑聚焦,压弯机构的设计要求为可高精度调节压弯力矩、结构具备高刚性和高稳定性,可避免或减弱镜体的拉伸、挤压、扭曲。为了满足技术指标,本设计采用了基于Weak-Link[19]的柔性铰链压弯机构,如图 4所示。
|
图 4 柔性铰链压弯机构原理示意图 Figure 4 Schematic diagram of flexure hinge mechanism. |
该型压弯机构具备如下特点:
1) 高精度、高刚性和高稳定性:采用的Weak-Link柔性铰链,是基于光刻技术的光化学加工工艺制作[20],8mm厚的层状柔性铰链机构由40层厚度为200μm刻蚀薄片堆叠而成。这种加工工艺可以在超高调节精度的情况下保证柔性铰链的位置高精度、结构高刚性和高稳定性。
2) 避免镜体的拉伸、压缩:镜体在压弯过程中,作为工作面的镜表面弯曲且被压缩,而镜中心面则保持稳定。基于这个特点,镜子的每端被多组柔性铰链对固定(见图 4上的A-A′、B-B′、C-C′、D-D′、E-E′),弯矩的旋转中心与镜体中心面重合,每组圆形柔性铰链对的轴线均相交于镜中心面上同一个点O。这种结构可确保O点在压弯前后的位置变化量极小,这样镜体压弯时受到拉伸或压缩的影响足够小,可以忽略不计。由于镜体的曲率半径较大、面形起伏较小、调节精度高,因此采用高精度高、小量程的圆形柔性铰链对。
3) 等力矩压弯:为了保证结构稳定性,采用了等力矩压弯模式,即镜子两端施加相同的力矩。两端通过电机驱动近似等量的位移来施加力矩,可便于压弯调节。
4) 较长力臂压弯:在满足刚性和稳定性的基础上,采用较长的力臂压弯。较长的臂长可以保证电机能施加足够的压弯力矩,同时长臂的适度变形也能增加力矩调节的精度。
2 压弯机构的有限元分析及镜体的优化镜体的设计基于几何精确压弯理论[17],但是要想获得理想的压弯面形,压弯镜的宽度需要多次的优化,来补偿由机构、工艺等带来的误差。从ESRF[21-22]提供的经验来看,对装置进行有限元分析(Finite Element Analysis, FEA),并根据结果对镜体宽度进行优化是一个可行的方法。
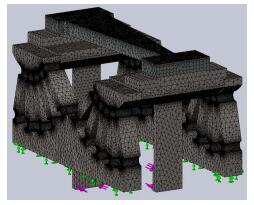
2.1 压弯机构的有限元分析图 5-7为压弯机构的有限元分析模型图。光学参数选择如下:源距p=6m,像距q=0.08m,掠入射角θ=3mrad,镜体厚度t=0.0055m,镜中心宽度b0=0.0127m,镜子材料硅的弹性模量E=1.124×1011Pa,根据几何精确压弯理论[17],压弯力矩:
| $ M = \frac{{4{a_2}E{I_0}}}{{2(1 + {a_2}t)}} $ | (2) |
|
图 5 压弯机构有限元分析网格划分图 Figure 5 3-D model of the flexure bending mechanism with solid mesh for FEA. |
|
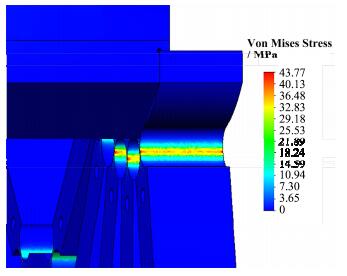
图 6 柔性铰链有限元分析应力图 Figure 6 The stress diagram of flexure hinge for FEA. |
|
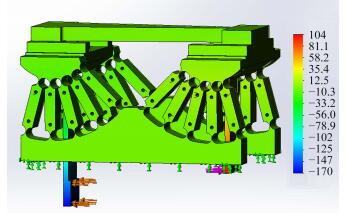
图 7 压弯机构有限元分析水平位移图 Figure 7 The displacement diagram of bending mechanism for FEA. |
其中:a2表示椭圆方程级数展开系数:
| $ {a_2} = \frac{{(p + q)\sin \theta }}{{4pq}} $ | (3) |
则压弯力矩M=0.376N·m,故可算得压弯机构有限元分析时,长压弯力臂的载荷为5.945N,短压弯力臂的载荷为7.635N。
根据有限元分析结果,柔性铰链的最大应力约为43MPa,远小于因瓦-36合金的屈服强度(276MPa),证明此装置可以在材料弹性范围内工作。此外,长压弯力臂的受力点水平位移约为149μm,短压弯力臂的受力点水平位移约为88.4μm。
2.2 镜体宽度优化的理论基础压弯机构压弯效率的最终检测方案是探测压弯镜体表面的位移,并计算出曲率半径分布,与理论椭圆面形进行对比。
由于压弯机构的设计方案是确定的,所以我们可以根据有限元分析中探测计算出的镜表面曲率分布与理论曲率分布的关系,来优化镜体的宽度,从而使实际镜表面的曲率分布接近于理论值。
在几何精确压弯理论[17]中,理论曲率半径分布为:
| $ {R_{\rm{c}}}(x) = \frac{{{{({{Z'}^2} + 1)}^{3/2}}}}{{Z''}} + \frac{t}{2} $ | (4) |
式中:Z′与Z″为标准椭圆面形方程的一阶和二阶导数。
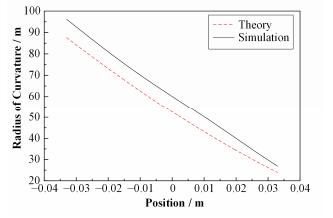
根据以上公式可计算出理论曲率半径分布rs(图 8中Theory线),实际镜表面的曲率半径分布r(图 8中Simulation线)则根据有限元分析中探测的镜体表面中心线坐标及Y方向位移数据,经MATLAB数据处理后由式(4) 计算得出,如图 8所示。
|
图 8 镜体镜表面曲率与理论曲率 Figure 8 Comparison of surface curvature between simulation and theoretical calculation of mirror. |
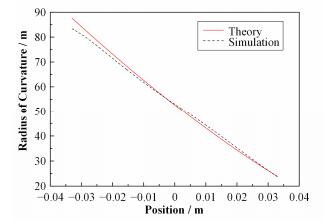
由图 8可看出,实际曲率半径分布整体大于理论曲率半径分布,这是由于施加的压弯力有一部分用来克服压弯机构自身阻力。我们需要将这部分力的影响排除。采用的方法就是计算实际曲率半径与理论曲率半径的平均比值,之后将压弯力乘以两者比值。优化后对比如图 9所示。
|
图 9 镜表面曲率分布与理论曲率分布优化对比 Figure 9 Comparison of surface curvature distribution and theoretical curvature distribution of mirror. |
根据式(1),式中的b0、E、M(s)、I0均为已知数,则可得出b(s)与ρ(s)成定系数的正比例关系。若用b1表示当前镜体的宽度分布,b2表示优化后镜体的宽度分布,则b1与b2的关系可表示为:
| ${b_2} = \frac{{{b_1} \cdot {r_{\rm{s}}}}}{r}$ | (5) |
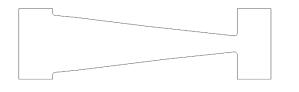
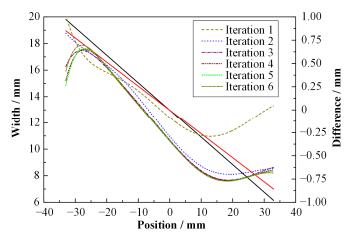
根据式(5) 和对原镜体的有限元分析结果,我们对镜体宽度进行了6次迭代优化,最终的镜体工程图如图 10所示,每次迭代优化后的镜体宽度与原镜体的宽度差分布如图 11所示,其中实线为原镜体的宽度分布,虚线为宽度差分布曲线。
|
图 10 优化后镜体工程图 Figure 10 Engineering drawing of optimized mirror. |
|
图 11 迭代优化镜体与原镜体宽度差分布 Figure 11 Distribution of the width difference between the iterative mirrors and the original mirror. |
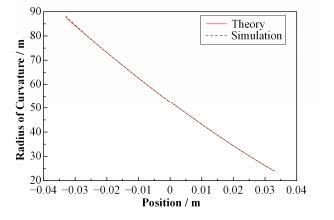
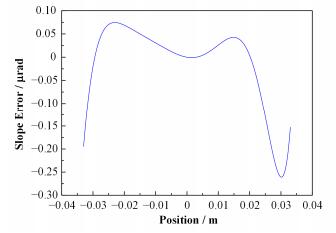
最终优化后的镜体压弯后的表面曲率半径分布与理论分布对比如图 12所示。经过最终优化的镜体经压弯后的曲率半径分布相较于理论值的误差已经很小。为进一步检测压弯镜体面形与标准面形的误差,我们计算出优化后的压弯镜体上表面的斜率误差分布如图 13所示,由图 13可知,优化后的压弯镜体的最大斜率误差约400nrad,斜率误差的均方根值(Root Mean Square, RMS)值经MATLAB计算为89nrad。根据光斑经验方程:
| $W = \sqrt {{A^2} + {B^2} + {C^2}} $ | (6) |
|
图 12 优化后镜体曲率半径对比 Figure 12 Comparison of curvature radius of optimized mirror between theory and simulation. |
|
图 13 优化后镜体表面斜率误差 Figure 13 Slope errors of the optimized bent mirror. |
式中:A表示衍射极限分辨率,为100nm;B表示光斑压缩比,根据前文所述的光学参数计算为125nm;C为误差展宽,计算公式为:
| $C = {S_{{\rm{RMS}}}} \cdot 2 \cdot 2.355 \cdot q$ | (7) |
式中:SRMS为斜率误差的RMS值。根据计算,以上优化后的镜体在理论上可以将光斑聚焦到164nm。
3 实验测量与对比将柔性铰链压弯机构与变宽度镜体装调后,成功构建了非球面压弯镜机构(图 14)。装调好的压弯镜机构采用上海光源自主研发的长程面形仪(Long Trace Profiler, LTP) LTP-1200[23-24]进行了压弯面形的离线测试。

|
图 14 压弯机构样机 Figure 14 Prototype of the bending mechanism. |
压弯机构采用驱动悬臂的方式施加力矩。由于实际测试过程中无法直接测量力矩,因此只能测量压弯力臂的位移间接推算压弯力矩。压弯镜的一个重要特点是光学参数具有可调性。之前的研究结果表明[25],针对特定参数(如源距、像距、掠入射角等)设计的压弯镜,可以通过调节力矩的方式压弯产生具有新参数的非球面形并保持较小的面形误差。考虑到压弯机构调节特性和压弯镜具有光学参数可调性[26-29],因此离线测试分析采用如下步骤:
1) LTP离线测试;2) 数据初步分析;3) 调节悬臂位移,继续离线测试;4) 面形分析及压弯力矩的拟合计算;5) 面形误差分析。
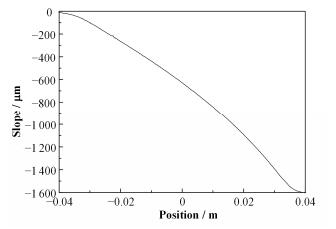
经反复调节后测试得到的斜率分布见图 15。
|
图 15 实际测量压弯镜斜率分布 Figure 15 Slope curve of bent mirror in experiment. |
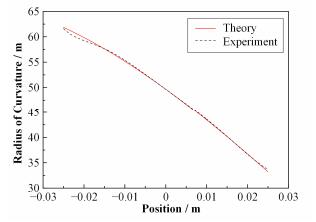
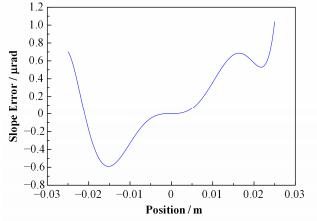
根据斜率分布图,取镜体的工作长度为5cm进行斜率分布的计算,根据几何精确压弯理论[17]对实测参数下的理论面形的曲率半径分布进行拟合(图 16),根据斜率与面形误差的关系[17]计算出实测的面形误差分布(图 17)。
|
图 16 实测压弯镜曲率半径分布 Figure 16 Radius of curvature of bent mirror in experiment compared with theorial calculation. |
|
图 17 实际测量压弯镜面形斜率误差分布 Figure 17 Slope errors of the bent mirror in experiment. |
经过计算,实际测量的压弯镜面形斜率误差的RMS值为430nrad。将该面形误差导入式(6) 和(7),计算得出在不考虑光束线误差的情况下,该压弯机构能够将光斑聚焦到230nm。
4 讨论基于上海光源硬X射线微聚焦及应用线站的光束线条件,在几何非球面镜精确压弯理论[17]的基础上设计并分析了高精度柔性铰链压弯机构。采用LTP-1200型号长程面形仪离线测试了压弯镜面形,并完成了数据分析。LTP测试结果表明,本文设计的柔性铰链压弯机构与匹配的镜体装配,压弯非球面形产生的面形误差RMS值约430nrad,理论上可在BL15U1线站实现230nm的硬X射线聚焦光斑。该光斑尺寸略大于164nm的有限元分析和优化设计的结果,其误差主要来源于镜子和压弯机构的装配误差,以及压弯机构与基座的安装应力。
本文系统性地开展了柔性铰链压弯机构的物理设计、有限元分析优化和LTP的离线测试工作。LTP测试结果与有限元分析结果基本相符,表明本文设计的压弯机构能够实现硬X射线的亚微米聚焦,并验证了基于精确压弯理论的有限元设计和优化方法的有效性,对进一步实现更高空间分辨率的纳米聚焦压弯镜具有指导意义。
| [1] | Snigirev A, Kohn V, Snigireva I, et al. A compound refractive lens for focusing high-energy X-rays[J]. Nature, 1996, 384: 49–51. DOI: 10.1038/384049a0 |
| [2] | Evans-Lutterodt K, Stein A, Ablett J M, et al. Using compound kinoform hard-X-ray lenses to exceed the critical angle limit[J]. Physical Review Letters, 2007, 99: 134801. DOI: 10.1103/PhysRevLett.99.134801 |
| [3] | Yan H F. X-ray nanofocusing by kinoform lenses:a comparative study using different modeling approaches[J]. Physical Review B, 2010, 81: 075402. DOI: 10.1103/physrevb.81.075402 |
| [4] | Schroer C G, Lengeler B. Focusing hard X rays to nanometer dimensions by adiabatically focusing lenses[J]. Physical Review Letters, 2005, 94(5): 054802. DOI: 10.1103/physrevlett.94.054802 |
| [5] | Bergemann C, Keymeulen H, van der Veen J F. Focusing X-ray beams to nanometer dimensions[J]. Physical Review Letters, 2003, 91(20): 204801. DOI: 10.1103/physrevlett.91.204801 |
| [6] | Kruger S P, Neubauer H, Bartels M, et al. Sub-10 nm beam confinement by X-ray waveguides:design, fabrication and characterization of optical properties[J]. Journal of Synchrotron Radiation, 2012, 19(2): 227–236. DOI: 10.1107/s0909049511051983 |
| [7] | Mimura H, Yumoto H, Matsuyama S, et al. Efficient focusing of hard X rays to 25 nm by a total reflection mirror[J]. Applied Physics Letters, 2007, 90(5): 051903. DOI: 10.1063/1.2436469 |
| [8] | Mimura H, Handa S, Kimura T, et al. Breaking the 10 nm barrier in hard-X-ray focusing[J]. Nature Physics, 2009, 6(2): 146. DOI: 10.1038/nphys1457 |
| [9] | Chao W, Harteneck B D, Liddle J A, et al. Soft X-ray microscopy at a spatial resolution better than 15 nm[J]. Nature, 2005, 435(7046): 1210–1213. DOI: 10.1038/nature03719 |
| [10] | Chao W, Kim J, Rekawa S, et al. Demonstration of 12 nm resolution fresnel zone plate lens based soft X-ray microscopy[J]. Optics Express, 2009, 17(20): 17669–17677. DOI: 10.1364/oe.17.017669 |
| [11] | Suzuki Y, Takeuchi A, Takenaka H, et al. Fabrication and performance test of fresnel zone plate with 35 nm outermost zone width in hard X-ray region[J]. X-ray Optics and Instrumentation, 2010, 2010: 6. DOI: 10.1155/2010/824387 |
| [12] | Kang H C, Yan H F, Winarski R P, et al. Focusing of hard X-rays to 16 nanometers with a multilayer Laue lens[J]. Applied Physics Letters, 2008, 92(22): 221114. DOI: 10.1063/1.2912503 |
| [13] | Kang H C, Stephenson G B, Liu C, et al. Sectioning of multilayers to make a multilayer Laue lens[J]. Review of Scientific Instruments, 2007, 78(4): 046103. DOI: 10.1063/1.2713439 |
| [14] | Yan H F, Rose V, Shu D M, et al. Two dimensional hard X-ray nanofocusing with crossed multilayer Laue lenses[J]. Optics Express, 2011, 19(16): 15069–15076. DOI: 10.1364/oe.19.015069 |
| [15] | Barrett R, Härtwig J, Morawe C, et al. X-ray optics at the ESRF[J]. Synchrotron Radiation News, 2010, 23(1): 36–42. DOI: 10.1080/08940880903547363 |
| [16] | Zhang L L, Yan S, Jiang S, et al. Hard X-ray micro-focusing beamline at SSRF[J]. Nuclear Science and Techniques, 2015, 26(6): 060101. DOI: 10.13538/j.1001-8042/nst.26.060101 |
| [17] | Mao C W, Yu X H, Xiao T Q, et al. Exact revision of the elliptically bent mirror theory[J]. Applied Optics, 2011, 50(16): 2413–2417. DOI: 10.1364/ao.50.002413 |
| [18] | Mao C W, Jiang H, He Y, et al. Compensation for gravitational sag of bent mirror[J]. Nuclear Instruments and Methods in Physics Research Section A, 2017, 853: 20–26. DOI: 10.1016/j.nima.2016.12.020 |
| [19] | Shu D, Toellner S, Alp E. Modular overconstrained weak-link mechanism for ultraprecision motion control[J]. Nuclear Instruments and Methods in Physics Research Section A, 2000, 467-468(2001): 771–774. DOI: 10.1016/s0168-9002(01)00499-5 |
| [20] | Shu D, Toellner T S, Alp E E. Redundantly constrained laminar structure as weak-link mechanisms[P]. US Patent No.6984335, 2006. http://www.freepatentsonline.com/6607840.html |
| [21] | Zhang L, Baker R, Barrett R, et al. Mirror profile optimization for nano-focusing K-B mirror[C]. AIP Conference Proceedings, 2010:801-804. DOI:10.1063/1.3463335. |
| [22] | Kelez N, Chuang Y, Smith-Baumann A, et al. Design of an elliptically bent refocus mirror for the MERLIN beamline at the advanced light source[J]. Nuclear Instruments and Methods in Physics Research Section A, 2007, 582: 135–137. DOI: 10.1016/j.nima.2007.08.092 |
| [23] | Xiao T Q, Xia S J. New long trace profiler for aspheric optical surface metrology[J]. Proceedings of SPIE, 2002, 4927: 208–213. DOI: 10.1117/12.471438 |
| [24] |
罗红心, 王劼, 肖体乔. 大尺度非球面光学元件的高精度检测[J].
光电产品与资讯, 2013, 3(5): 39–41.
LUO Hongxin, WANG Jie, XIAO Tiqiao. High precision inspection of large scale aspheric optical elements[J]. OE Product and News, 2013, 3(5): 39–41. |
| [25] |
毛成文, 余笑寒, 肖体乔. 变宽度压弯椭圆柱面聚焦镜的光学参数可调性[J].
核技术, 2009, 32(5): 333–336.
MAO Chengwen, YU Xiaohan, XIAO Tiqiao. Tunability of optical parameters of width-variable bent elliptical microfocus mirror[J]. Nuclear Techniques, 2009, 32(5): 333–336. |
| [26] | Zhang L, Hustache R, Hignette O, et al. Design optimization of a flexural hinge-based bender for X-ray optics[J]. Synchrotron Radiation, 1998, 5: 804–807. DOI: 10.1107/s0909049597015288 |
| [27] | Underwood J H, Thompson A C, Kortright J B, et al. Focusing X-rays to a 1 μm spot using elastically bent, graded multilayer coated mirrors[J]. Review of Scientific Instruments, 1996, 67: 3359. DOI: 10.2172/603683 |
| [28] | Yang B X, Rivers M, Schildkamp W, et al. GeoCARS microfocusing Kirkpatrick-Baez mirror bender development[J]. Review of Scientific Instruments, 1995, 66(2): 2278–2280. DOI: 10.1063/1.1145663 |
| [29] | Howells M R, Cambie D, Duarte R M, et al. Theory and practice of elliptically bent X-ray mirrors[J]. Optical Engineering, 2000, 39(10): 2748–2762. DOI: 10.1117/1.1289879 |


