2. 中国科学院大学 北京 100049;
3. 重庆理工大学 重庆 400054
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Chongqing University of Technology, Chongqing 400054, China
X射线反射镜是同步辐射光源、自由电子激光、大型天文望远镜等领域的重要光学元件,其品质直接决定了相关领域实验结果的好坏。长程面形检测系统如:LTP[1-4] (Long Trace Profiler)、NOM[5-6] (Nanometer Optical Component Measuring Machine)、DLTP[7] (Development LTP)、ESAD[8] (Extended Shear Angle Difference)等,是这类大尺度光学元件的重要检测仪器。为了满足第三代同步辐射光源、自由电子激光等领域对X射线反射镜品质的更高要求,X射线反射镜的检测系统需要做到在大角度范围内(比如10mrad范围内)检测精度优于50nrad。对于如此高的检测需求,传统长程面形检测系统的测量精度需要进一步提升。
传统长程面形检测系统是基于f-theta系统原理来实现对待测镜面面形进行检测。在传统长程面形检测系统中,通过引入一束沿固定方向入射的光束在待测镜面上逐点扫描,待测镜面的反射光束形成测量光束,当待测镜面上不同测量点间倾角改变角度θ时,测量光束将会产生2θ的角度改变。通过测量光束的角度变化,可以得到待测镜面的面形信息,实现对待测镜面进行检测。
为了提高长程面形检测系统的检测精度,在过去20多年间,许多研究人员对传统长程面形检测系统进行了大量的改进,提出了各种具体系统误差源的处理方案[9-15]。其中,由长程面形检测系统中各光学元件加工缺陷引入的误差[4, 16-17]也是研究的重点之一。
当各光学元件加工好以后,由于加工精度的限制,在光学元件的表面会出现加工缺陷,这种加工缺陷将会改变入射光的既定传播方向,对角度测量引入误差。对于透射体光学元件,其介质折射率的不均匀也会导致光束在透射体中传播时发生偏离,从而对角度测量引入误差。
在对镜面进行检测时,待测镜面上不同点的角度不同,对应的测量光束将入射到测量系统中不同光学元件的不同位置,形成测量光束在光学元件上的横移。测量光束在不同光学元件上的横移量越大,所引入的角度误差可能就越大。当测量角度范围较大时,这类误差可达到微弧度量级。对大范围高精度角度测量而言,这是必须要消除或减小的系统误差源。
要消除或减小这类由光学元件加工缺陷引入的误差,通常有两种方法:首先,可以通过提高长程面形检测系统中每个光学元件的品质来减少由单个光学元件加工缺陷引入的误差。但受加工技术条件的限制,光学元件总会出现加工缺陷,通过提高光学元件的品质来减小其引入的误差往往是非常困难且非常昂贵的;其次,光学元件加工缺陷引入的误差是测量光束口径区域内的平均值,若在两次测量中,测量光束在光学元件上的横移量很小,则光学元件对这两次测量角度的差值引入的误差可以忽略。所以,除了应用高品质的光学元件减小误差以外,还可以通过巧妙的光学设计来减少测量光束在光学元件上的横移量以及减少光路系统中光学元件的数量,来减少由光学元件加工缺陷引入的误差。
Qian等[4]提出了改进的长程面形检测系统的设计方案,以减少长程面形检测系统中各测量光束在各光学元件上的横移量。Barber等[17]提出利用双反射镜代替长程面形检测系统中的五棱镜以减少由介质折射率不均匀以及入射面加工缺陷引入的角度误差。但是由于对待测镜面进行检测时为了保护待测镜面,待测镜面与系统光学元件间需要预留特定的操作空间[4]。在进行大角度范围检测时,测量光束在光学元件上的横移量很难减小,光学元件上的缺陷就会因为横移量而引入测量误差。为了降低这类误差的影响,传统的方法是对测量结果进行校正,但由于测量过程中诸多不确定因素的影响,这样的校正工作也是很困难的[18]。为了实现大角度范围内高精度角度检测,光学元件的加工缺陷是一个必须要减小的误差源。
为了减小由于测量光束横移及光学元件加工缺陷引入的测量误差,本文提出了基于法线追迹原理的高精度角度测量系统方案。通过法线追迹原理设计的面形检测系统,既可以为待测镜面预留足够大的操作空间,又能大大减少测量光束在光学元件上的横移量,从而减小由光学元件加工缺陷引入的测量误差。
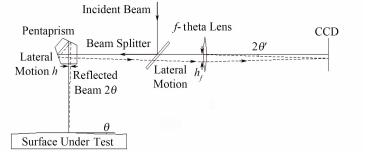
1 长程面形检测系统原理长程面形检测系统是基于f-theta原理发展起来的高精度角度检测系统。如图 1所示,入射光束经分束镜、五棱镜反射后垂直入射到待测镜面,待测镜面反射的光束形成测量光束。若待测镜面上测量点处与水平面成θ角,则测量光束与入射光束成2θ反射回五棱镜。测量光束经过五棱镜、分束镜后入射到f-theta系统,经f-theta系统的透镜聚焦后在位于焦平面的电耦合元件(Charge-coupled Device, CCD)上形成测量光斑。通过确定测量光斑的位置可以得到测量光束的角度。通过沿待测镜面子午方向逐点移动五棱镜,则可测出待测镜面在子午方向的面形数据。
|
图 1 长程面形检测系统原理 Figure 1 Principle of long trace profiler system. |
当测量待测镜面上不同点时,由于测量点的角度改变以及测量点到测量系统中各光学元件光程的改变,测量光束将会在光学元件上横向移动,正是这种测量光束的横移导致了系统光学元件不同位置的加工缺陷对测量角度引入误差。
从图 1可以看出,光学元件距离测量点光程越大,对同样的测量角度θ,测量光束在光学元件上的横移量就越大,光路中光学元件越多,测量角度θ'中的误差也就越大。
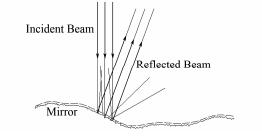
光学元件加工好后,因为加工精度的限制其表面会出现加工缺陷(图 2)。在长程面形检测系统中,其所用到的测量光束口径往往在毫米量级,这样的光束入射到光学表面后,加工缺陷中的高频缺陷将导致部分测量光线以杂散光的形式反射,其低频缺陷将会导致测量光束偏离理想的传播方向,只有这部分引入低频加工缺陷信息的测量光束能够被测量到。所以对于反射镜面而言,毫米量级的测量光束相当于是对加工缺陷进行了平滑处理,只有平滑后的低频误差(图 2中虚线)进入了测量结果。
|
图 2 测量光束对镜面缺陷的平滑效应 Figure 2 Smoothing effect of probe beam on the manufacture defect of a reflected surface. |
对于透射体而言,其介质存在不均匀性,这会导致测量光线偏离理想方向从而引入角度测量误差。对于毫米量级的测量光束,当光束通过透射体后,其效果也相当于是对透射体缺陷进行了平滑处理,只有低频不均匀性引入的误差能进入测量结果。
文献[16]对由于表面加工缺陷及介质不均匀性引入的误差进行了比较详细的分析,对于口径为20mm、折射率为1.5的透射光学元件,如果其表面存在±1nm(峰谷值(Peak-to-Valley, P-V))正弦形面形缺陷,其将有可能引入约157nrad的角度测量误差,而对于同样的反射表面其将有可能引入约628nrad的角度测量误差。目前光学元件表面加工的最高精度约为λ,此类光学元件极其昂贵。
对于介质不均匀性而言,如果相应的光学元件采用目前最高品质(等级H5或等级0AA)的美国康宁玻璃(折射率不均匀性约为δn=5e-7),对于约2mm厚的光学元件而言,其引入的角度误差也可能达到约157nrad。
文献[16]的分析可以看出,就算采用最好的材料、运用最好的加工工艺得到的光学元件,要想在大角度范围内实现误差优于50nrad的高精度角度测量,对于传统的长程面形检测系统而言,现有的光学元件加工品质很难满足要求。
在利用长程面形检测系统进行角度测量时,只有测量角度的相对变化量是需要的结果。虽然加工缺陷一定会对测量角度引入误差,但如果在测量不同角度时,光学元件加工缺陷引入的测量误差都相同,或者变化很小,则对测量的角度差而言,这样的光学元件相当于没有引入误差。
在长程面形检测系统中某光学元件加工缺陷引入的误差经测量光束平滑后的低频部分ε,可以展开为测量光束在该光学元件上横移量h的级数:
| $\varepsilon = \sum\nolimits_{m = 0}^\infty {{A_i}{h^i}} $ | (1) |
式中:Ai为常数,设相邻两次不同位置测量角度分别为θ1、θ2,测量光束在该光学元件上的横移量分别为h1、h2,则该光学元件对两次测量角度所引入的误差分别为:
| ${\varepsilon _1} = \sum\nolimits_{m = 0}^\infty {{A_i}h_1^i} $ | (2) |
| ${\varepsilon _2} = \sum\nolimits_{m = 0}^\infty {{A_i}h_2^i} $ | (3) |
对测量角度的相对变化量
| $\Delta \varepsilon = {\varepsilon _1} - {\varepsilon _2} = \sum\nolimits_{m = 0}^\infty {{A_i}(h_1^i - h_2^i)} $ | (4) |
若两次测量光束的相对横移量
| $\Delta \varepsilon = \sum\nolimits_{m = 1}^\infty {i{A_i}h_1^{i - 1}\Delta h} $ | (5) |
从式(5) 可以看出,若能减小测量光束的相对横移量Δh,则可以减小光学元件对测量角度相对变化量Δθ引入的误差Δε。
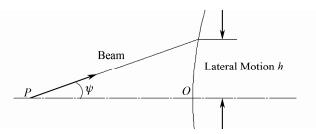
设入射到某光学元件的测量光束与该光学元件光轴相交于P点(图 3),从交点P到光学元件的距离为LOP,当测量光束角度Ψ较小时,测量光束与光轴之间的横移量可近似表示为:
| $h = {L_{OP}} \times \mathit{\Psi} $ | (6) |
|
图 3 测量光束与光轴的横移量 Figure 3 Lateral motions of probe beam from optical axis. |
由于长程面形检测系统是通过逐点扫描的方式对待测镜面面形进行检测,在测量不同点的角度时,对于测量系统中的某个光学元件而言,对应的距离LOP及入射到该光学元件上的测量光束的角度Ψ均会发生变化。在测量不同点时,对应的测量光束的相对横移量Δh可表示为:
| $\Delta h = \Delta {L_{OP}} \times \mathit{\Psi} + {L_{OP}} \times \Delta \mathit{\Psi} $ | (7) |
从式(7) 可以看出,相对横移量Δh可分为两部分。要减小式(7) 中的第一部分,至少要求ΔLOP或Ψ非常小。对于移动五棱镜式的长程面形检测系统(如NOM、DLTP等),ΔLOP往往可达到几百毫米甚至上千毫米,这要求在放置待测镜面时,待测镜面应该尽可能水平放置以减小Ψ。而对于移动扫描头式的长程面形检测系统(如LTP II[19]),ΔLOP主要来源于待测镜面面形起伏以及气浮导轨起伏,在整个测量过程中其变化量约在微米量级。通过调整待测镜面姿态减小Ψ后,对于这类系统,式(7) 中的第一部分可以忽略不计。
对式(7) 中的第二部分
从式(5) 可以看出,当测量光束横移量Δh较小时,由系统光学元件加工缺陷引入的误差正比于测量光束的横移量Δh:
| $\Delta \varepsilon = (\sum\nolimits_{m = 1}^\infty {i{A_i}h_1^{i - 1}} )\Delta h = C\Delta h$ | (8) |
式中:C为比例系数。
通过调整待测镜面姿态减小式(7) 中Ψ以后,Δh主要来自于式(7) 中的第二部分。对同样的角度变化ΔΨ,Δh正比于LOP:
| $\Delta h \approx {L_{OP}} \times \Delta \mathit{\Psi} $ | (9) |
从式(8)、(9) 可以看出,当测量光束的相对横移量较小时,光学元件所引入的误差正比于入射光线与光轴交点到该光学元件的距离LOP。
| $\Delta \varepsilon = D \times {L_{OP}}$ | (10) |
式中:D为比例系数。
从图 1可以看出,对传统的长程面形检测系统,要减小LOP只能要求长程面形检测系统中所有的光学元件尽可能地靠近待测镜面上的测量点。但是为了保护待测镜面[4],需要为待测镜面预留一定的操作空间。对系统中各光学元件而言,LOP往往能达到几百毫米甚至上千毫米。所以对于传统的长程面形检测系统而言,要实现为待测镜面保留一定的操作空间,同时又要减小系统光学元件加工缺陷引入的角度测量误差,这样的系统往往是很难实现的。
2 法线追迹原理传统的长程面形检测系统是通过测量待测镜面反射光束的角度变化来实现对待测镜面面形测量。在这个系统里,待测镜面反射的光束包含了待测镜面面形的信息。如果能够通过其他方式获得一束包含待测镜面面形信息的光束,通过测量该光束的角度变化也能获得待测镜面的面形信息。基于这样的思路,本文提出法线追迹原理。
图 4是第一类法线追迹原理光路示意图。在图 4中,点光源被放置在小孔的中心。由点光源发出的光入射到镜面,经镜面反射的光返回小孔,这部分反射回的光线只有一部分能通过小孔并向小孔后传播。通过这样的体系我们总能从点光源发出的光线中筛选出一光束。
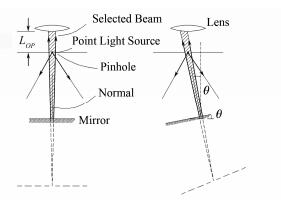
|
图 4 基于点光源的法线追迹系统 Figure 4 Normal tracing method based on point light source. |
图 4中镜面以下的虚线是镜面对小孔成的像及筛选出的光束的反向延长线。通过小孔筛选出的光束可以看成是由孔像的中心点发出的光束,从简单的几何光学原理可知,这样的一束光总是沿镜面的法线方向传播且具有一定锥角的光束。其锥角的大小由孔到镜面间的距离及孔的口径决定。当镜面旋转一个角度θ时,通过小孔选择的光束也旋转θ角。
从图 4中还可以看出,通过法线追迹原理筛选出的光束总是通过小孔,对于光路系统中的光学元件(比如图 4中透镜)其用于计算光束横移量的距离LOP是从小孔到该光学元件的光程。所以只要将系统中的光学元件尽可能地靠近小孔,则可以减小测量光束在该光学元件上的横移量,从而减小该光学元件加工缺陷引入的角度误差。对于待测镜面而言,小孔与待测镜面间可以留出很大的操作空间,这样在减小系统光学元件加工缺陷引入误差的同时又为待测镜面留出了较大的操作空间,从而解决了传统长程面形检测系统所面临的两难问题。
图 5是第二类法线追迹原理的光路示意图。与图 4基于点光源的法线追迹原理不同,图 5基于面光源的法线追迹系统其光源不用放置在小孔中心。面光源发出的光被小孔限制后,只有少部分光能通过小孔入射到待测镜面,待测镜面反射的光被小孔筛选后透过小孔的部分形成测量光束。小孔筛选出来的光束也是一束沿待测镜面上测量点处法线方向传播的光束。该光束具有一定的发散角,其发散角的大小由孔的口径及孔到镜面间的距离决定。运用图 5的光路系统,能够实时选出一束沿待测镜面测量点处法线方向传播的光束。通过测量该光束的角度值就能够获得待测镜面的面形数据。
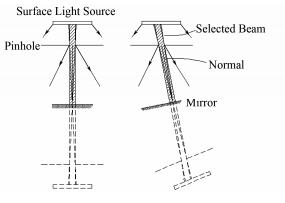
|
图 5 基于面光源的法线追迹系统 Figure 5 Normal tracing system based on surface light source. |
基于法线追迹原理可以设计出许多新型的长程面形检测系统,在进行设计时为了减少系统中光学元件加工缺陷引入的误差,我们需要将相应的光学元件尽可能地靠近法线追迹系统中的小孔,并且减少系统中所用到的透射或反射光学元件的数目。
图 6是基于点光源法线追迹原理设计的长程面形检测系统。在图 6中点光源、小孔、分束镜(Beam Splitter, BS)、傅里叶变换透镜(Fourier Transform Lens, FT Lens)及CCD放置在平移台上形成长程面形检测系统的扫描头。
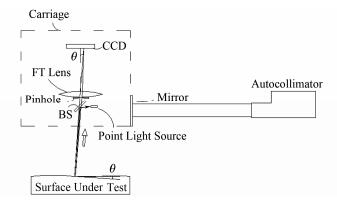
|
图 6 基于点光源法线追迹原理的长行程面形检测系统 Figure 6 Long trace profiler system based on point light source normal tracing principle. |
由点光源发出的光经过BS反射后入射到待测镜面,通过适当调节点光源、BS及小孔的位置,由BS反射的光可以看成是由小孔中心发出的光,由待测镜面反射的光透过BS后被小孔筛选,通过小孔的光束形成测量光束。该测量光束是一束沿待测镜面上测量点处法线方向传播的光束。傅里叶变换透镜紧靠小孔放置,并将测量光束汇聚到CCD处形成测量光斑。
图 6中紧贴扫描头放置的反射镜与放置于光学平台的自准直仪形成角度校正系统,用于校正测量过程中平移台转动引入的角度测量误差。对于高精度的平移台,在运行过程中其引入的转动角度约在微弧度量级,在校正系统中光束的横移量约在微米量级,相对于几十毫米口径的校正光束,该横移量可忽略不计。
从图 6可以看出,在该测量光路中所用到的透射、反射光学元件只有傅里叶变换透镜及分束镜。由于傅里叶变换透镜紧贴小孔放置,测量光束在傅里叶变换透镜上引起的光束横移量是非常小的。分束镜可以尽可能地靠近小孔放置,这样测量光束在分束镜上的横移量也能做到非常小。
由式(10) 可知,在横移量较小时光学元件加工缺陷引入的测量误差正比于测量光束与光轴的交点到光学元件的距离LOP。在传统的长程面形检测系统中,LOP可能达到几百甚至上千毫米。而在本文提出的系统中,只要将相应的光学元件紧贴小孔放置,LOP可以做到几个毫米甚至更小。对于同样的光学元件,在本系统中其引入的角度测量误差将有可能比在传统系统中小约两个数量级。
图 7是基于面光源法线追迹原理设计的长程面形检测系统。与图 6不同的是,在图 7中小孔与BS紧贴放置,面光源发出的光被小孔后的分束镜反射到待测镜面,待测镜面反射回来的光束通过小孔部分形成测量光束。在这个系统中,分束镜与小孔紧贴放置,测量光束在分束镜上的横移量几乎为零。分束镜后的傅里叶变换透镜可以紧贴分束镜放置,从而减小傅里叶变换透镜上测量光束的横移量。
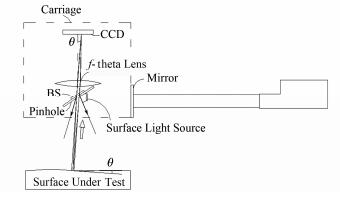
|
图 7 基于面光源法线追迹原理的长行程面形检测系统 Figure 7 Long trace profiler system based on surface light source normal tracing principle. |
对于基于点光源的法线追迹系统,若点光源与小孔中心位置不重合,则会引入角度测量误差。由于测量光束都是经过小孔的光束,在理想情况下测量光束角度的改变等于经过小孔中心光线角度的改变,如图 8所示,其中:h为小孔到镜面间距离;dv、dh为小孔中心与点光源竖直及水平方向的偏移量。
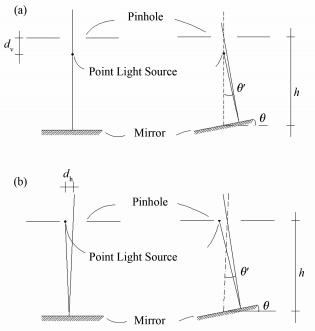
|
图 8 点光源与小孔中心位置偏离引入误差(a)在竖直方向偏离dv,(b)在水平方向偏离dh Figure 8 Diagram of systematic errors introduced by position deviations of point light source and the center of the pinhole with vertical position deviation dv (a) and horizontal position deviation dh (b). |
从图 8可以看出,当点光源中心与小孔中心存在偏离时,当待测镜面角度改变θ时,测量光束的角度改变量为θ'。在利用长程面形系统进行角度测量时,只有不同测量点间角度的相对改变量具有测量意义,由光源点位置变化引入的角度测量误差Δθ可以定义为:
| $ \Delta \theta = ({\theta '_1}-{\theta '_0})-({\theta _1}-{\theta _0}) $ | (11) |
式中:θ0为镜面的初始角度;θ1为镜面转动后的角度。转动角度θ=θ1-θ0,对应的测量角度分别为θ'0及θ'1,通过简单的几何关系可以得到:
| $\Delta {\theta _{\rm{v}}} = \arctan (\frac{{{d_{\rm{v}}}}}{{2h + {d_{\rm{v}}}}}\tan ({\theta _1})) - \arctan (\frac{{{d_{\rm{v}}}}}{{2h + {d_{\rm{v}}}}}\tan ({\theta _0}))$ | (12) |
| $\Delta {\theta _h} = \arctan (\frac{{{d_{\rm{h}}}}}{{2h - {d_{\rm{h}}}\tan ({\theta _1})}}) - \arctan (\frac{{{d_{\rm{h}}}}}{{2h - {d_{\rm{h}}}\tan ({\theta _0})}})$ | (13) |
式中:Δθv与Δθh分别为光源点与小孔中心存在竖直偏离及水平偏离引入的测量误差。
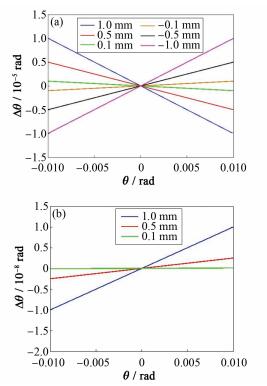
图 9是令式(12) 和(13) 中θ0等于0时计算得到的在不同的dv及dh时,测量角度误差与测量角度关系图。
|
图 9 点光源与小孔中心位置偏离引入误差分析(h=500 mm) (a)竖直方向偏离从-1mm到1mm时,(b)水平方向偏离从0.1mm到1mm时 Figure 9 Analysis of systematic errors introduced by position deviations of point light source and the center of the pinhole with h=500 mm. (a) Vertical position deviations within ±1 mm, (b) Horizontal position deviations from 0.1 mm to 1mm |
从图 9可以看出,当点光源与小孔中心存在竖直方向的偏离时会产生较大的系统误差。在测量量程范围内(如图 9中,±10mrad)这种由点光源位置与小孔中心偏离引入的误差具有很好的线性,在搭建系统时可以尽可能地调节点光源与小孔中心位置重合以减小这类误差,而对于剩余的这类系统误差,由于其具有很好的线性,可在最后系统定标环节进行消除。
对于基于面光源的法线追迹系统,则不存在此类问题。
4.2 光强均匀性引入误差分析传统的LTP系统在进行测量时采用同一束光束对不同测量点进行测量,与此不同的是,基于法线追迹原理的系统采用的是从同一扩展光源筛选出的不同光束,当测量不同角度时测量光束存在横向强度分布的变化,在CCD上的测量光斑能量分布也会随之发生相应的改变,这种强度的变化会导致CCD上测量光斑质心位置改变,从而引入角度测量误差。
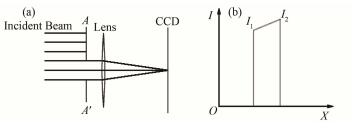
在ZEMAX软件的非序列模式下,我们构造类似图 10(a)的光学系统,通过设置平行光束的参数,可让平行光束产生类似图 10(b)的强度变化。
|
图 10 光源强度分布不均匀引入误差分析(a) ZEMAX模拟光路,(b)通过A-A′光阑后子午面内光强分布 Figure 10 Systematic errors introduced by beam intensity inhomogeneity. (a) Schematic of simulation system created in ZEMAX non-sequential mode, (b) Intensity distribution in the meridional plane of the incident beam |
在ZEMAX的非序列模式下,选用“Source Diode”光源来生成横向具有高斯分布的光束平行。
式(14) 为光源“Source Diode”横向光强分布关系,通过在ZEMAX中设置光源的X-Width、X-Sigma、X-Width Hx、Y-Width、Y-Sigma、Y-Width Hy等参数,获得横向高斯分布的平行光束。
| $I(x, y) = {I_0}\exp ( - 2({(\frac{x}{{{S_x}}})^{2{H_x}}} + {(\frac{y}{{{S_y}}})^{2{H_y}}}))$ | (14) |
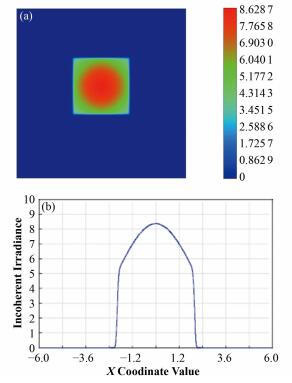
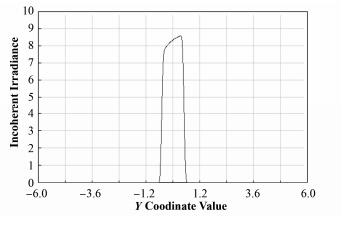
在光源传播方向上加上适当的光阑(图 10(a)中A-A′),则可以从类似图 11光强分布的光束中获得类似图 10(b)的强分布不均的平行光束(图 12)。
|
图 11 ZEMAX非序列模式小区域内横向强度高斯分布平行光束(a)高斯光束横向强度分布,(b)横向强度子午面内光束强度分布 Figure 11 Intensity distribution of Gauss beam generated within non-sequential mode of ZEMAX. (a) The transverse section, (b) The row cross-section |
|
图 12 通过光阑筛选出的光束子午面内光强分布 Figure 12 Intensity distribution of the row cross-section of the beam filtered by light diaphragm. |
设光束边缘最弱点与最强点光强分别为I1与I2,则差值I2-I1与最强点I2的比例S为:
| $S = \frac{{{I_2} - {I_1}}}{{{I_2}}}$ | (15) |
通过设置光源“Source Diode”的参数,得到不同比例S的光束。当不同比例S的平行光束经过类似图 10(a)的系统后,在CCD上可得到透镜聚焦后的测量光斑的光强分布。利用质心算法,可以得到不同光强分布S的光束在CCD上质心位置。比较不同比例S的光束在CCD上质心位置差别Δy,利用f-theta关系Δθ=fΔy(f为透镜焦距),可以计算出由于S引入的角度测量误差。
通过ZEMAX的模拟可以比较测量光束强度变化对CCD处测量光斑质心位置影响。经过ZEMAX模拟图 10(a)的系统后发现,当S < 4%时,光强不均匀性引入的误差小于60nrad。
4.3 光源强度分析基于法线追迹原理的面形测量系统是从光源发出的光线中选出一小部分来进行测量,对于同样的光源,其所获得的光束强度比传统LTP系统要弱许多,若最后在CCD上不能获得足够强的测量光斑,则没法实现高精度测量。
若待测镜面为平面镜,设点光源强度为I0且分布于半锥角为ϕ的锥形区域内。设光源距待测镜面间距为h,小孔口径为d,则通过小孔选出的光束半锥角可近似表示为d/4h,光源光束对应立体角Ωs与小孔选出光束对应立体角Ωh可分别表示为:
| $\begin{array}{l} {\Omega _s} = 2{\rm{\pi }}\int_0^\phi {\sin \varphi d\varphi } \\ {\rm{ = }}2{\rm{\pi }}(1 - \cos (\phi )) \end{array}$ | (16) |
| $\begin{array}{l} {\mathit{\Omega} _h} = 2{\rm{\pi }}\int_0^{d/4h} {\sin \varphi d\varphi } \\ {\rm{ = }}2{\rm{\pi }}(1 - \cos (d/4h)) \end{array}$ | (17) |
则通过小孔选出光强可表示为:
| ${I_h} = {I_0}\frac{{1 - \cos (d/4h)}}{{1 - \cos (\phi )}}$ | (18) |
对于±10mrad量程的测量系统(图 6),设光源强度为1mW,分布于半锥角为12mrad的锥形区域内,待测镜面与小孔间距约为230mm,当小孔直径为1mm时,可得到测量光束总强度
根据图 6的光源系统,可在ZEMAX非序列模式下来分析CCD上获得的光强。在ZEMAX模拟过程中,光源、小孔直径及小孔到待测镜面间距与上面分析相同。通过软件模拟后,在透镜的焦平面上能获得总强度约1.6 μW的测量光斑,而测量光斑中心则达到了约740W·m-2的辐照度,这样强度的测量光斑足以满足大多数CCD探测需求,若采用强度大于1mw的光源则能获得更强的测量光斑。
从以上分析可看出,理论分析结果略大于ZEMAX模拟结果,这主要是因为ZEMAX在模拟过程中考虑了其他形式的光能损耗,如半反半透镜及透镜上多个分界面上光束来回反射造成的光能损失。利用式(18) 可以对测量光束光强进行初步估计。
4.4 横移量引入误差分析通过前面的分析可知,测量光束在系统光学元件上横移量越大,则其引入的系统误差可能越大(图 13)。
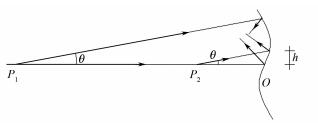
|
图 13 面形缺陷引入误差分析 Figure 13 Systematic errors introduced by surface figure error. |
图 13中,OP1与OP2为计算横移量对应的光程差;θ为测量角度差;h为测量光束横移量。从图 13可以看出,对于同样的角度差,P1位置测量光束间横移量大于P2位置,反射光束间的角度误差也因横移量而减少。
对于具有正弦形缺陷的反射镜面,其正弦形表面可表示为:
| $f(x) = A\sin (2{\rm{\pi }}x/D)$ | (19) |
在该光学表面上每个点,其法线方向偏离理想法线方向的角度为:
| $f'(x) = \frac{{2{\rm{\pi }}A}}{D}\cos (2{\rm{\pi }}x/D)$ | (20) |
式中:A表示正弦形缺陷的幅度;x为反射面上对应点的位置;D为反射面口径。由于是反射,面形缺陷在点x处引入的误差应为2f'(x)。
对于口径为20mm的反射表面,若其表面存在±1nm(P-V值)周期20mm的正弦形面形缺陷,则测量光线会在x=0mm处引入约628nrad的测量误差,在x=10mm处引入约-628nrad的测量误差。若待测面形上测量点到反射镜面间距(如图 13中OP1)为1m(在移动五棱镜式的长程面形系统中这个距离可能会大于1m,而对于移动扫描头式的系统这个距离可能达到几百毫米),设系统满量程为20mrad,则测量光束会经过该反射面的整个区域,若测量起始角度时光束位于镜面上x=0mm处,当测量角度差为10mrad时,光束将位于镜面上x=10mm处,则对于10mrad的角度差,该镜面将引入约1.256 μrad的角度误差。
若能减小测量光束的横移量,比如通过特殊的光路设计将图 13中的P1位置减小到P2位置,从图 13可以看出,对于同样的测量角度差θ,其引入的误差大为减少。
通过法线追迹方法,尽可能地将光学器件靠近小孔放置,若小孔到光学器件间的距离为10mm(紧凑放置时,此距离还可更小),在20mrad满量程内,横移量h最大为0.2mm,根据式(20) 由横移量引入的误差
| $\begin{array}{l} \Delta \theta = \frac{{4{\rm{\pi }}A}}{D}\left( {\cos (\frac{{2{\rm{\pi }}(x + h)}}{D}) - \cos (\frac{{2{\rm{\pi }}x}}{D})} \right)\\ {\rm{ }} = - \frac{{8{{\rm{\pi }}^2}A}}{{{D^2}}}\sin (\frac{{2{\rm{\pi }}x}}{D})h \end{array}$ | (21) |
从式(21) 可以看出,h越大引入的误差越大,则当h取最大0.2mm时,根据式(21) 得到在整个反射面区域内,测量角度量程为20mrad时该反射面形引入的误差(图 14)。
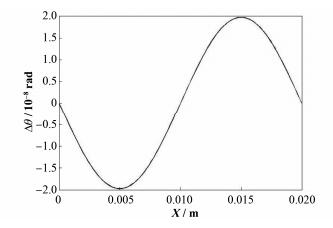
|
图 14 横移量为0.2mm时正弦形缺陷引入误差 Figure 14 Systematic errors introduced by surface figure error with beam lateral motion equals to 0.2mm. |
从图 14可以看出,当减小横移量后,相同缺陷的反射镜面对相同的角度测量量程,其引入的误差大大减小。
5 结语与传统的直接采用平行细光束的长程面形检测系统不同,本文通过法线追迹原理设计了新型的长程面形检测系统,在该系统中小孔与点光源或面光源通过适当的放置,可以用来筛选出沿待测镜面上测量点处法线方向传播的光束,实现对测量点处法线方向的自动追迹,通过测量不同点法线光束的角度变化,获得待测镜面的面形数据。
通过本文的分析可知,光学元件加工缺陷引入的角度测量误差正比于测量光束与光轴交点到光学元件的距离LOP。在传统的长程面形检测系统中,该距离往往在几百毫米甚至上千毫米,而且很难减小。在测量不同角度时,这样的距离会导致测量光束在系统光学元件上产生较大的横移量,从而引入光学元件上不同位置加工缺陷导致的角度测量误差。这类由系统光学元件加工缺陷引入的误差通常会达到几百纳弧度甚至微弧度量级,对于大范围内50nrad的高精度检测要求而言,这是一个必须要消除或减小的误差源。而在本文设计的系统中,通过将光学元件紧贴小孔放置,LOP可以减小到毫米量级。于是对于同样的光学元件,当应用于本文的系统中时,其所引入的角度测量误差将会被大大减小。
| [1] | Irick S C. Improved measurement accuracy in a long trace profiler:compensation for laser pointing instability[J]. Nuclear Instruments & Methods in Physics Research A, 1994, 347(1-3): 226–230. DOI: 10.1016/168-9002(94)91882-1 |
| [2] | Takacs P Z, Qian S N. Accuracy limitations in long-trace profilometry[C]. AIP Conference Proceedings, Sacramento, California, USA, 2004, 708:831-834. DOI:10.1063/1.1757924. http://scitation.aip.org/content/aip/proceeding/aipcp/10.1063/1.1757924 |
| [3] | Ritucci A, Rossi M. A long trace profiler with large dynamical range[C]. Proceedings of SPIE, 2013:8788. DOI:10.1117/12.2020915. |
| [4] | Qian S N, Qian K, Idir M. Advance in a nano-accuracy surface profiler with an extended-angle test range[J]. Nuclear Instruments and Methods in Physics Research A, 2013, 710: 52–58. DOI: 10.1016/j.nima.2012.10.106 |
| [5] | Siewert F, Noll T, Schlegel T, et al. The nanometre optical component measuring machine:a new sub-nm topography measuring device for X-ray optics at BESSY[C]. AIP Conference Proceedings, 2004, 705:847-850. DOI:10.1063/1.1757928. |
| [6] | Siewert F, Buchheim J, Boutet S. Ultra-precise characterization of LCLS hard X-ray focusing mirrors by high resolution slope measuring deflectometery[J]. Optics Express, 2012, 20(4): 4525–4536. DOI: 10.1364/OE.20.004525 |
| [7] | Lacey I, Artemiev N A. The developmental long trace profiler (DLTP) optimized for metrology of side-facing optics[J]. Proceedings of SPIE, 2014, 9206: 920603. DOI: 10.1117/12.2061969 |
| [8] | Schulz M, Ehret G, Stavridis M, et al. Concept, design and capability analysis of the new deflectometric flatness reference at PTB[J]. Nuclear Instruments and Methods in Physics Research A, 2010, 616: 134–139. DOI: 10.1016/j.nima.2009.10.108 |
| [9] | Yashchuk V V, Barber S, Domning E E. Sub-microradian surface slope metrology with the ALS developmental long trace profiler[J]. Nuclear Instruments and Methods in Physics Research A, 2010, 616(2-3): 212–223. DOI: 10.1016/j.nima.2009.10.175 |
| [10] | Lammert H, Senf F, Berger M. Improvement of synchrotron radiation mirrors below the 0.1-arcsec RMS slope error limit with the help of a long trace profiler[J]. Proceedings of SPIE, 1997, 3152: 168–179. DOI: 10.1117/12.295556 |
| [11] | Yashchuk V V. Positioning errors of pencil-beam interferometers for long trace profilers[J]. Proceedings of SPIE, 2006, 6317: 63170A. DOI: 10.1117/12.677956 |
| [12] | Yashchuk V V. Optimal measurement strategies for effective suppression of drift errors[J]. Review of Scientific Instruments, 2009, 80: 115101. DOI: 10.1063/1.3249559 |
| [13] | Siewert F, Buchheim J, Zeschke T. Characterization and calibration of 2nd generation slope measuring profiler[J]. Nuclear Instruments and Methods in Physics Research A, 2010, 616(2-3): 119–127. DOI: 10.1016/j.nima.2009.12.033 |
| [14] | Qian S N, Wayne L, Idir M. Nano-accuracy measurements and the surface profiler by use of monolithic hollow penta-prism for precision mirror testing[J]. Nuclear Instruments and Methods in Physics Research A, 2014, 759: 36–43. DOI: 10.1016/j.nima.2014.03.043 |
| [15] |
童新宇, 彭川黔, 何玉梅, 等. 长程面形仪测量数据的拟合方法[J].
核技术, 2016, 39(8): 080102.
TONG Xinyu, PENG Chuanqian, HE Yumei, et al. Curve fitting algorithm for measurement data of long trace profiler[J]. Nuclear Techniques, 2016, 39(8): 080102. DOI: 10.11889/j.0253-3219.2016.hjs.39.080102 |
| [16] | Qian S N, Takacs P Z. Modern metrology concerns[M]. Rijeka, Croatia: InTech, 2012: 77-114. |
| [17] | Barber S K. Developmental long-trace profiler using optimally aligned mirror based pentaprism[J]. Optical Engineering, 2011, 50(5): 053601. DOI: 10.1117/1.3572113 |
| [18] | Yashchuk V V, McKinney W R. Proposal for a universal test mirror for characterization of slope measuring instruments[J]. Proceedings of SPIE, 2007, 6704: 67040A–1. DOI: 10.1117/12.732719 |
| [19] | Qian S N, Qian K. Study and considerations of nanometer and nano-radian surface profiler[J]. Proceedings of SPIE, 2010, 7656: 76560D–1. DOI: 10.1117/12.871258 |


