冷却剂丧失事故(Loss of Coolant Accident, LOCA)是核电厂中常见的事故类型，是指一回路压力边界产生破口或发生破裂，或是阀门误开启导致的一回路冷却剂装量减少的事故。由于一回路高温高压的特性，当压力边界出现破口时，系统压力、流量、温度、放射性等状态参数会迅速失衡，同时核电厂的安全设备也将投入运行^[1]。LOCA事故的后果相对严重，即使发生中小破口也有导致堆芯熔毁的可能性（例如三里岛事故）。CPR1000核电厂的《状态导向法事故处理规程》^[2]中指出：“操纵员根据所能获得的信息，找出发生特定事件或事故的特有征兆，判明并确认瞬变或事故的种类与性质”。当LOCA事故发生时，操纵员易于将LOCA事故与其他类型的事故区分开，但难于判断LOCA的破口尺寸和破口位置，而不同的破口尺寸和位置将直接影响到事故的处置和后果。目前，操纵员仅能凭借仪表参数和操作经验对破口尺寸和位置进行诊断，但这样的诊断方式存在很大的风险。若能根据核电厂实时监控的状态参数自动诊断出LOCA事故的破口位置和尺寸并将信息提供给操纵员，将会减轻操纵员的压力，提高事故处理的准确性与效率。

随着人工神经网络(Artificial Neural Network, ANN)的兴起与发展，运用神经网络对核电厂事故进行诊断成为新的突破点^[3]。在国内外的研究中，已将多种类型的神经网络运用在了核电厂的故障诊断中^[4]。文献[5]将BP (Back Propagation)神经网络运用在AP1000核电厂的蒸汽发生器泄压阀或安全阀误开启、蒸汽系统管道破裂、丧失正常给水与给水管道破裂这4类事故的诊断中，诊断结果较为准确。文献[6]利用遗传算法对蒸汽发生器的U型管破裂事故进行故障诊断仿真，诊断结果准确地识别出了发生破口的蒸汽发生器。文献[7]将BP神经网络和RBF (Radial Basis Function)神经网络相结合，对5类典型的核电厂设计基准事故进行了诊断，在诊断耗时和准确率上均取得了较好的效果。在调研中发现，基于神经网络的诊断研究多集中在区分不同事故类型上，尚未有对LOCA事故中破口尺寸和破口位置进行诊断的详细研究。本文以CPR1000核电系统为对象^[8]，将BP神经网络、Elman神经网络、RBF神经网络和支持向量机运用在LOCA事故的诊断中，验证了神经网络用于LOCA事故诊断的可行性并对比了4种神经网络方法的诊断效果。其中，支持向量机在选取多项式核函数和利用GSA (Grid Search Algorithm)算法或PSO (Particle Swarm Optimization)算法对c、g参数进行寻优后，可达到接近100%的诊断准确率。

人工神经网络是一种受生物神经网络启发建立的数据处理算法，具有强大的模式识别和数据拟合能力。本文选取了常用的BP神经网络、有反馈的Elman神经网络、有空间变换的RBF神经网络和支持向量机这4种各具特点的神经网络算法用于诊断研究。

BP神经网络是一种多层前馈神经网络，信号从输入层进入隐含层最终到达输出层，误差则反向传播。网络内部利用测试误差不断反向地调整权值和阈值，使输出结果不断地逼近期望的输出结果，从而实现模式识别的功能。BP神经网络的传递函数一般选取sigmoid函数，学习过程属于有监督的方式，因此需要使用带有目标输出的样本集。当训练数据完成对神经网络的训练后，输入测试数据就可以进行模式识别^[9]。BP神经网络的缺陷在于容易陷入局部最优而无法逼近目标输出。

RBF神经网络是一种三层的前向网络，由输入层、隐含层和输出层构成。在隐含层中一般采用径向基函数将输入向量空间转换到隐含层空间中，这样就实现了将原来线性不可分的情况转换成线性可分的情况^[10]。RBF神经网络的学习过程同样是有监督的学习方式。RBF神经网络结果简单、学习收敛速度快，能逼近任意的非线性函数。

Elman神经网络是一种有反馈的神经网络，网络的结构一般有4层，分别为输入层、隐含层、承接层和输出层^[11]。其中，输入层用于传入数据；隐含层利用非线性的传递函数对数据进行变换；输出层用于线性加权输出；承接层用来记忆隐含层单元前一时刻的输出值并返回给网络的输入，可以认为一个一步延时算子^[12]。由于存在承接层，其对于历史状态的数据具有敏感性，增强了网络的模式识别能力。

支持向量机(Support Vector Machine, SVM)由Vapnik^[13]在20世纪90年代基于统计学理论提出，是机器学习和数据挖掘领域的有力工具。支持向量机基于结构风险最小化和VC (Vapnik-Chervonenkis Dimension)维理论，通过建立一个分类超平面也可称为决策曲面，使在决策曲面两侧数据之间的隔离边缘最大化来实现模式识别的功能^[14]。

超平面的方程可表示为：ωx+b=0，最优分类超平面所要达到的目的有两个：一是要将两类样本正确地区分开，使模型训练误差为零；二是使分类间隔达到最大。

要实现准确地对样本进行分类，需要满足：

要使分类间隔达到最大，需要满足：

对于类似核电系统的非线性问题，可以在约束条件中引入一个松弛因子ε_i (ε_i≥0)，松弛因子的引入是为了允许一定的分类误差。上述两个条件可修改为：

式中：0 < ε_i < 1说明样本都被正确地进行了分类；ε_i≥1说明x_i被错误分类。$C\mathop \sum \limits_{i = 1}^l {\varepsilon _i}$可理解为一个惩罚项，C用于控制对错分样本的惩罚程度。

对该问题，可以利用拉格朗日函数将最优分类问题转化为其对偶形式：

经计算，最优权值向量和最优偏置分别为：

因此，最优分类超平面可表示为：

最优分类函数为：

在非线性问题中，将原空间数据点通过非线性变换到高维空间内，这一变换通过核函数完成。为了实现不同类型的模式分类，可选取不同类型的核函数K(x_i, x)。常见的核函数类型有^[15]：

线性核函数：

多项式核函数：

径向基核函数：

Sigmoid核函数：

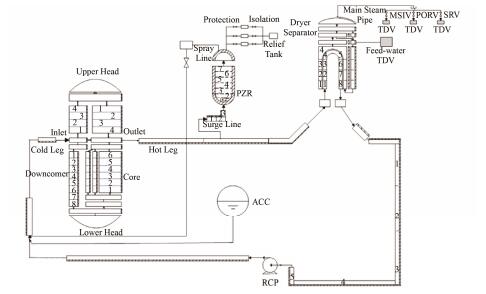
由于真实核电厂的事故状态参数难以获取，因此本文利用CATHARE程序对核电厂事故进行了模拟。CATHARE是一款应用于压水堆的安全分析程序，可计算事故状态下的热工水力学参数和进行安全评价^[16]。本文利用该程序对CPR1000核电系统进行建模，如图 1所示。在此基础上模拟了冷管段和热管段分别出现1-9 cm破口的情况，并提取了事故发生后6种热工水力参数0-500 s的变化值，具体参数类型如表 1所示。发生LOCA后的事故序列如表 2所示。

图 1

图 1 CPR1000一回路建模 Figure 1 The CPR1000 model of the primary loop.

表 1

表 1 LOCA事故参数 Table 1 Accident parameters of LOCA. 破口位置Location of break 破口尺寸Size of break / cm 热工水力参数Thermal-hydraulic parameters 冷管段Cold-leg 1, 2, 3, 4 稳压器压力Pressure of pressurizer 热管段Hot-leg 5 环路流量Loop flow 6 堆芯入口温度Inlet temperature of reactor core 7 堆芯出口温度Outlet temperature of reactor core 8 蒸汽发生器蒸汽压力Steam pressure of steam generator 9 蒸汽发生器蒸汽流量Steam flow of steam generator

表 1 LOCA事故参数 Table 1 Accident parameters of LOCA.

表 2

表 2 LOCA事故序列（冷管段5 cm破口） Table 2 Accident sequence of LOCA (5-cm break in cold-leg). 事件Accident sequence 时间Time / s 破口发生Break happens 0 停堆信号Scram signal 43.748 安注信号Safety injection signal 64.735 停止给水信号Stop feedwater signal 69.964 打开辅助给水信号Open auxiliary water signal 125.12

表 2 LOCA事故序列（冷管段5 cm破口） Table 2 Accident sequence of LOCA (5-cm break in cold-leg).

LOCA事故中稳压器压力、环路流量、堆芯入口温度、堆芯出口温度、SG蒸汽压力和SG蒸汽流量的各时点参数值将作为神经网络的输入量，破口位置和尺寸作为网络输出量，利用多种神经网络对破口位置和破口尺寸进行诊断。

在模拟计算得到的6种热工水力参数中，由于0-200 s处于安全设备投入阶段，参数跳动范围较大而无法诊断。因此提取200-500 s的各时点参数值用于训练和测试网络。网络的训练样本集利用60%的数据，其余40%的数据用于测试样本集的构建。

本文首先利用BP神经网络、Elman神经网络和RBF神经网络对破口尺寸进行诊断，诊断准确率如表 3所示。BP神经网络的诊断准确率最低且极不稳定，Elman神经网络的准确率要优于BP神经网络，但依然不能达到要求。BP神经网络和Elman神经网络的准确率低是因为他们都采用了误差梯度下降算法。当误差函数不是严格的凸函数时，就会存在局部极小点，当误差梯度下降到这些点时就会停留在该处而无法继续下降，但这些点却不是全局的最小误差点，因此实际输出与期望输出的差距较大。RBF神经网络对LOCA破口尺寸的诊断准确率较高，在大多数情况下都达到了100%的精度。

表 3

表 3 神经网络对破口尺寸的诊断结果 Table 3 The diagnosis results of break sizes by ANN methods. 破口尺寸 Break size / cm 冷管段破口Cold-leg break 热管段破口Hot-leg break BP神经网络 BP ANN / % Elman神经网络 Elman ANN / % RBF神经网络 RBF ANN / % BP神经网络 BP ANN / % Elman神经网络 Elman ANN / % RBF神经网络 RBF ANN / % 1 50.00 100.00 100.00 80.00 100.00 100.00 2 73.00 96.67 91.67 70.00 100.00 100.00 3 67.67 100.00 100.00 89.42 99.17 94.17 4 69.83 100.00 100.00 74.25 96.67 100.00 5 80.00 100.00 100.00 80.00 98.33 100.00 6 60.67 98.33 100.00 59.25 96.67 100.00 7 74.00 81.67 100.00 88.75 82.50 100.00 8 69.67 100.00 100.00 85.00 88.33 100.00 9 78.33 98.33 100.00 76.33 100.00 100.00

表 3 神经网络对破口尺寸的诊断结果 Table 3 The diagnosis results of break sizes by ANN methods.

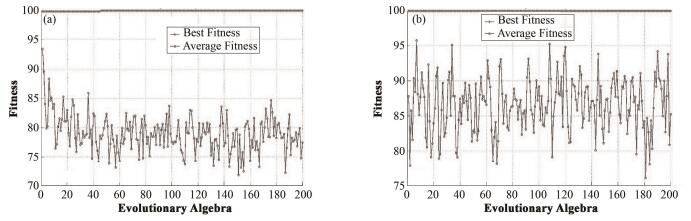
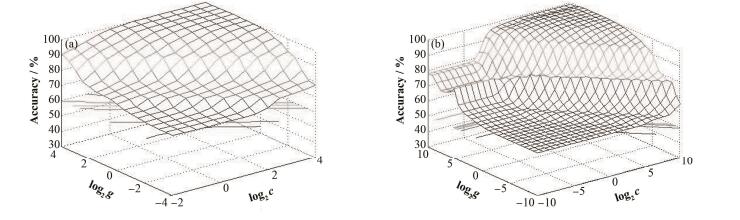
除以上三种神经网络方法外，本文还利用了支持向量机方法^[17]对破口尺寸进行了诊断。在进行诊断前，首先利用PSO算法和GSA算法对支持向量机中关键的惩罚参数(c)与核函数参数(g)进行了寻优^[18]。PSO算法通过对鸟群捕食行为的模仿来求解最优化问题，具有算法简单易行、收敛速度快和内部参数设置少的特点，已广泛运用于算法优化领域。GSA算法通过在参数搜索区域内划分网格，然后遍历网格内的所有参数点进行寻优。由于是对所有区域进行搜索，所以可以克服陷入局部最小值的问题。PSO算法对c、g参数寻优的适应度曲线如图 2所示。GSA算法对c、g参数寻优的准确率变化趋势如图 3所示。将PSO方法和GSA方法计算得到的最优c、g参数分别带入支持向量机中，对破口尺寸进行了诊断，结果见表 4。经过参数优化后的支持向量机对破口尺寸的诊断准确率在冷管段破口尺寸较大时出现少数未达到100%准确性的情况，其余均达到了100%的准确率。

图 2

图 2 PSO方法对SVM内c、g值寻优的适应度曲线(a)冷管段破口，(b)热管段破口 Figure 2 The fitness curves of SVM optimized by PSO to confirm c and g. (a) Cold-leg break, (b) Hot-leg break

图 3

图 3 GSA方法对SVM内c、g值寻优的准确率变化曲线(a)冷管段破口，(b)热管段破口 Figure 3 The accuracy curves of SVM optimized by GAS to confirm c and g. (a) Cold-leg break, (b) Hot-leg break

表 4

表 4 参数优化后的支持向量机对破口尺寸的诊断结果 Table 4 The diagnosis results of break sizes by optimized SVM. 破口尺寸 Break size / cm 冷管段Cold-leg break 热管段Hot-leg break PSO / % c=5.772 4, g=6.464 1 GAS / % c=5.656 9, g=5.656 9 PSO / % c=11.628 0, g=244.137 4 GSA / % c=21.112 1, g=111.430 5 1 100.00 100.00 100.00 100.00 2 100.00 100.00 100.00 100.00 3 100.00 100.00 100.00 100.00 4 100.00 100.00 100.00 100.00 5 100.00 100.00 100.00 100.00 6 100.00 100.00 100.00 100.00 7 95.00 95.00 99.17 100.00 8 100.00 100.00 100.00 100.00 9 98.33 98.33 100.00 100.00

表 4 参数优化后的支持向量机对破口尺寸的诊断结果 Table 4 The diagnosis results of break sizes by optimized SVM.

在支持向量机中，核函数的作用是将原空间样本非线性变换到高维空间中，不同的变换方式必然导致变换后的样本分类难度存在差异，因此本文针对影响支持向量机诊断性能的三种核函数：线性核函数、多项式核函数与RBF核函数^[19]进行了探究。将三种核函数用于热管段和冷管段1-9 cm破口尺寸的诊断后，得到的结果如表 5所示。表 5中的准确率表示对9类(1-9 cm)破口尺寸诊断准确率的平均值。从表 5数据可以看出，多项式核函数的效果最优，其次是RBF核函数，线性核函数的效果最差。

表 5

表 5 三种核函数的诊断结果 Table 5 The diagnosis results of 3 types of kernels. 破口位置 Location of break 诊断准确率Accuracy of diagnosis / % 线性核函数Linear kernel 多项式核函数Polynomial kernel RBF核函数RBF kernel 热管段Hot-leg 79.80 100.00 99.66 冷管段Cold-leg 68.01 100.00 98.65

表 5 三种核函数的诊断结果 Table 5 The diagnosis results of 3 types of kernels.

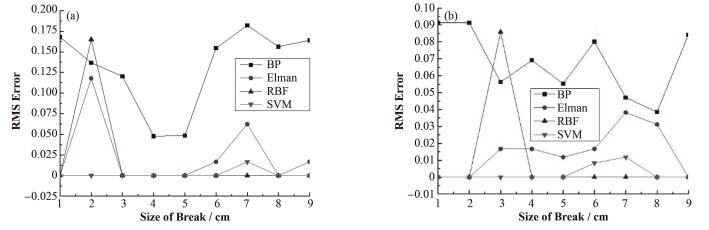
将神经网络用于核电厂的事故诊断，除了要考虑诊断的准确率外，还应考虑诊断的稳定性。因此本文对以上所涉及的4种神经网络的诊断稳定性进行了研究。将4种神经网络对相同破口位置和破口尺寸进行20次重复诊断实验，并计算了20次实验结果的均方根(Root Mean Square, RMS)误差，如图 4所示。BP神经网络和Elman神经网络的诊断稳定性较差，RBF神经网络在破口尺寸较小的情况下表现出较大的不稳定性。支持向量机在4种网络中的稳定性最好，且在大多数情况下都能达到0，表明支持向量机在多次诊断时不会存在结果的波动性。

图 4

图 4 诊断结果的均方根误差(a)冷管段破口，(b)热管段破口 Figure 4 he RMS error of diagnosis. (a) Cold-leg break, (b) Hot-leg break

除对破口尺寸识别外，本文还利用了神经网络方法对破口位置进行了识别。BP神经网络、RBF神经网络、Elman神经网络和支持向量机对破口位置识别的准确率如表 6所示。结果表明，这4种神经网络对于破口位置的诊断准确度相似，都可以达到较高的精度。这是由于破口位置的诊断只涉及两种类型，因此易于区分。

表 6

表 6 4种神经网络对破口位置的诊断结果 Table 6 The diagnosis result of break location by 4 types of ANN methods. 破口位置 Location of break 诊断准确率Accuracy of diagnosis / % BP神经网络 BP ANN Elman神经网络 Elman ANN RBF神经网络 RBF ANN 支持向量 SVM 冷管段Cold-leg 99.66 99.66 100.00 99.66 热管段Hot-leg 99.33 99.33 99.33 98.65

表 6 4种神经网络对破口位置的诊断结果 Table 6 The diagnosis result of break location by 4 types of ANN methods.

1) BP神经网络、Elman神经网络、RBF神经网络和支持向量机对于LOCA事故中破口位置和破口尺寸的诊断均可以达到一定的识别精度，因此利用神经网络方法对LOCA事故类型进行诊断具有较强的可行性。

2) 对比4种神经网络可以发现：BP神经网络的误差较大且分布不均匀、收敛速度较慢；Elman神经网络的诊断准确率不高且耗时过长；RBF神经网络的准确率较高但在某些情况下诊断稳定性较差；支持向量机在选取多项式核函数和对c、g参数进行寻优后，可近似达到100%的准确率。因此在LOCA事故的诊断中，参数优化后的支持向量机是最佳的选择。

3) 该研究的缺陷在于核电厂事故数据是利用计算机程序模拟获得，与实际发生事故时的状态参数可能存在一定偏差，从而影响神经网络判断的准确性。因此考虑在今后的研究中利用已发生的真实的核电厂事故数据训练网络，并在事故发生时接收核电厂实时数据实现事故的在线诊断。