2. 中国科学院大学 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
固态熔盐堆是由美国科学家于2003年提出的第四代反应堆堆型之一[1],其主要特点包括:1) 使用氟化物熔盐冷却(熔盐堆);2) 使用三向同性(Tri-structural Isotropic, TRISO)包覆颗粒燃料(高温气冷堆)。包覆颗粒燃料元件有球形和柱形两种基本类型,其特点是能够在高温下运行,具有本征的安全性。固态燃料钍基熔盐堆(Thorium Molten Salt Reactor-Solid Fuel, TMSR-SF1) 是中国科学院“未来先进核裂变能”战略性先导科技专项优先选择并设计的两种反应堆堆型之一。2012年4月,中国科学院TMSR专项启动第一个固态燃料钍基熔盐堆的设计和建造[2]。该堆型采用球形燃料元件,利用熔盐冷却剂把固态燃料球产生的裂变能有效传递到热力系统进行能量转换。
核反应堆的运行是多物理场相互作用的过程,对核反应堆的分析研究已从单纯的中子物理学分析、热工水力分析、燃料性能分析、结构材料应力分析和系统响应分析,发展到如今的多物理场耦合分析。中子物理与热工耦合计算在反应堆分析中具有重要意义,其结果可用于更好地理解反应堆中的复杂现象。耦合计算时,分别使用中子物理计算程序和热工水力计算程序计算相同的模型问题并在迭代过程中交换数据,直到结果收敛达到稳定状态。
针对多种熔盐堆堆型的物理分析已有较多研究。Cheng等[3]针对熔盐快堆开发了三维稳态模拟程序,并用于模拟熔盐快堆的稳态运行状况。薛春等[4]则设计了一种将燃料球装入燃料组件的熔盐堆堆芯并对其进行了设计计算。Kophazi等[5]通过耦合DALTON和THERM程序,构建了一个三维耦合程序,并应用于MSRE稳态和瞬态多物理耦合分析。Zhang等[6]则针对2 MW熔盐实验堆的屏蔽层计算了中子注量分布和温度分布。Guo等[7-8]采用MCNP (Monte Carlo N Particle Transport Code)与多通道热工水力程序耦合的方式分析了简化的MSRE堆芯稳态功率分布、温度分布、压降和流量分配,并对堆芯设计进行了优化。Zhou等[9]采用MCNP与CFD (Computational Fluid Dynamics)热工水力程序耦合的方法,模拟了几种堆芯条件骤变时液态燃料熔盐堆的瞬态情况。而Li等[10]通过将PB-AHTR (Pebble Bed Advanced High Temperature Reactor)堆芯模型作为基础,利用清华大学自主开发的RMC (Reactor Monte Carlo codes)中子输运程序和热工水力程序CFX耦合,分析了固态燃料钍基熔盐堆稳态条件下该方法的准确性及耦合效率。何杰等[11]采用MCNP和ANSYS Fluent两种程序,利用Python语言编写了后处理程序MTF (MCNP to Fluent)并对液态熔盐堆TMSR-LF1的主屏蔽体开展了耦合计算分析。本文以TMSR-SF1为主要研究对象,以中子输运程序MCNP和热工水力程序ANSYS Fluent分别开展了TMSR-SF1的三维中子物理和三维热工水力模拟计算,通过C++编程语言进行上述两个模拟程序的数据交换以达到多物理耦合的目的,并对模拟结果中耦合前后的部分中子物理和热工水力指标进行了分析比较。本文对球床堆堆芯活性区的TRISO颗粒模型进行了简化以提高计算效率,并利用燃料球的堆积模块对球床进行了合理的划分,使球床堆的耦合数据交换得以进行。
1 计算方法及模型 1.1 堆芯结构TMSR-SF1堆芯包括堆芯活性区和石墨反射层,如图 1所示,其中活性区由燃料球随机堆积的球床和流经球床的熔盐组成,熔盐冷却剂在燃料球间的间隙中流动。上下圆台和侧面的环绕石墨构建了反射层,中间圆柱区为活性区,在反射层设有中子源、停堆系统、实验测量等专用通道。燃料元件为直径6 cm的固态燃料球,其中燃料UO2中235U富集度为17%,每个燃料球装有7.0 g铀。一回路冷却剂采用含高富集度7Li (99.995%)的FLiBe (2LiF-BeF2)熔盐。

|
图 1 TMSR-SF1堆芯示意图(a)横截面,(b)竖截面 Figure 1 Structure diagram of TMSR-SF1. (a) Cross section, (b) Vertical section |
以图 1堆芯模型为基础,建立中子物理模型用于蒙特卡罗方法计算,其中包括堆芯活性区、上下及侧面反射层、冷却剂腔室、控制棒通道等。
1.2 堆芯物理计算由于TMSR-SF1所装载的一万多个燃料球由基体石墨和包含有数千个TRISO燃料颗粒组成,而TRISO颗粒由4层包覆层和燃料核心构成,对如此众多的燃料球建模并得到精确计算结果是非常耗时的。因此,Fratoni等[12]提出通过将TRISO颗粒中的包覆层与基体石墨按照原子数之比合算成一种材料并保留燃料核心,从而达到简化模型结构、缩短计算时间的目的。表 1是对TMSR-SF1所使用燃料球的计算结果对比,从表 1中发现,该方法可用于TMSR-SF1并有效地缩短计算时间。
| 表 1 同质化TRISO颗粒效果 Table 1 Effect of TRISO particle homogenization. |
由于蒙特卡罗方法在计算有效增殖因子和反应率计数时存在概率性误差,因此在进行耦合模拟前,对该模型进行了所需中子数及计算误差分析。本文计算中每次迭代中子数为50 000,迭代次数为550次,跳过前50次迭代,计算的标准误差为0.000 16,统计误差小于0.1,计算时间约4 h。
进行中子物理计算所用截面数据库是在ENDF/B-Ⅶ数据库基础上,采用了针对熔盐高温特点加工的数据库ACEDATA,此截面数据库选取了300-2200 K之间共30个温度点,通过NJOY加工而成。堆芯活性区轴向向上划分为11层,径向按照燃料球体心立方堆积模块,每层划分为88份,总共836个栅元,并对其使用F7计数卡计数以供后续功率密度计算。
1.3 热工水力计算使用CFD方法进行针对球床堆堆芯的热工水力模拟研究中,球床的复杂性经常造成所需网格数庞大且难以得到精准的计算结果。Wu等[13]针对高温气冷堆HTGR (High Temperature Gas-cooled Reactor)的球床模型,运用CFD软件对比了真实燃料球间隙通道和多孔介质模型通道的计算结果,得出了多孔介质模型可用于计算堆芯活性区中冷却剂整体温度、流速、沿程压降、密度等主要参数的结论。因此,本文采用多孔介质模型描述燃料球球床结构,以简化网格、节省计算资源。
1.3.1 模型介绍热工水力模型根据中子物理模型的堆芯活性区冷却剂流动区域建立,包括上下石墨反射层的冷却剂通道及堆芯活性区,具体结构如图 2所示。该模型使用ANSYS ICEM划分网格,并与物理模型的相关区域在空间上完全重合。

|
图 2 热工水力模型示意图 Figure 2 Structural diagram of thermal-hydraulic model. |
1) 下反射层冷却剂入口通道边界条件。冷却剂进入下反射层入口通道,由下至上经过堆芯活性区并通过上反射层冷却剂通道离开堆芯。本文将各冷却剂入口通道流速设置为TMSR-SF1概念设计报告中参数,平均流速0.2235 m·s-1,最大流速0.744m·s-1,最小流速0.033 m·s-1,冷却剂入口温度设置为873.15 K。
2) 内热源加载。堆芯活性区内热源通过将MCNP计算得到的沉积能量转换为对应空间的功率密度,再通过耦合程序导入到设定热工水力模型功率密度、空间坐标信息的UDF (User-defined Function)中,内热源设置根据不同坐标位置加载对应的功率密度。
3) 其他边界条件。出口边界条件设置为压力出口。考虑重力影响,设置重力加速度为9.8 m·s-2。采用SIMPLE算法二阶迎风格式。
1.4 耦合过程冷却剂密度随温度的变化、核反应截面随温度的变化以及堆芯结构材料的热膨胀是中子物理模拟中最为重要的温度反馈信息[14]。本文耦合过程中热工水力模拟仅考虑温度及冷却剂密度变化的影响。
1.4.1 数据交换通过外耦合的方式耦合MCNP和ANSYS Fluent。在每一耦合循环中,两个模型分别进行计算,并通过C++语言开发程序完成数据交换过程。堆芯活性区在两个模型中皆在轴向分隔为11层;在每一次耦合循环中,耦合程序将中子物理模型中11层的沉积能量数据转换为功率密度并用于更新热工水力模型中内热源设置的更新。耦合步骤概括为如下步骤,图 3显示了模拟数据在两程序之间的传递过程。

|
图 3 MCNP与ANSYS Fluent耦合流程图 Figure 3 Coupling process between MCNP and ANSYS Fluent. |
1) MCNP以冷态堆芯为初始条件进行中子物理计算,从输出文件提取F7卡对各栅元的平均裂变沉积能计数,通过式(1) 转为功率密度:
| $ {P_i} = \frac{{{{({F_f})}_i}}}{{\sum\nolimits_i {{{({F_f})}_i}{V_i}} }}P $ | (1) |
式中:Pi是第i个栅元的功率密度,W·m-3;(Ff)i是第i个栅元裂变沉积能量,MeV;Vi是第i个栅元的体积,m3;P是反应堆堆芯热功率,W。
2) 以此功率密度分布更新ANSYS Fluent内热源设置,并进行热工水力计算,得到堆芯活性区温度分布和密度分布。
3) 以温度和密度分布数据更新MCNP输入文件中的栅元密度信息和调取的截面库,再次计算。
4) 比较前后两次中子物理计算结果中的有效增殖因子大小,判断耦合过程是否收敛。当偏差较大时,重复2)-4) 步骤的操作。
1.4.2 核反应截面的多普勒展宽多物理耦合的重要环节之一即更新中子物理计算的核反应截面。本文所采用的截面库更新方法为伪材料法[15]。通过伪材料法更新截面库,可大幅减少计算所需截面库的存储体积,且无需预处理截面库,节省计算资源;此方法的缺点是在更新MCNP计算的截面库时,并不是直接产生目标温度点所对应的截面库,而是通过计算目标温度点所在温度区间的上下两组截面库的比例分数,近似拟合截面库数据,且无法拟合热中子散射截面库S(α, β)数据,需要选择与目标温度最接近的温度点的热中子散射截面。
各核素的核反应截面自ACEDATA提取,在MCNP计算温度信息更新后,由式(2) 计算新的温度点所需提取截面库的分数:
| $ {f_1}(T) = \frac{{\sqrt {{T_2}}-\sqrt T }}{{\sqrt {{T_2}}-\sqrt {{T_1}} }} $ | (2) |
式中:T为新的栅元温度;T1和T2分别为截面库中T所在区间的最高温度和最低温度;f1为最低温度对应的核截面所占份额。所求栅元温度对应的截面为:
| $ \sum {(T) = {f_1}\sum {({T_1})} } + (1-{f_1})\sum {({T_2})} $ | (3) |
本文所使用的中子物理模型计算每次迭代使用50000个粒子,计算结果中有效增殖因子为1.04031,概念设计报告计算结果为1.03990,计算误差为0.0394%。
热工计算结果精度虽足够高,但在实际工程应用中达到毫米量级的流速变化对主要参数无明显影响,因此保留三位有效数字。热工水力模型耦合前后入口截面平均速度均为0.233 m·s-1,耦合情况下出口截面平均流速为0.215 m·s-1。未耦合情况下出口截面平均温度为903.935 K,耦合情况下出口截面平均温度为904.035 K,计算误差为0.01%。
耦合程序的验证采用Hu等[16]针对使用MCNP和Fluent进行中子物理与热工水力耦合可行性研究所采用的模型,对比手动输入功率密度与耦合程序转换的计算结果来验证计算方法是否正确。
验证模型由10 cm×10 cm×10 cm的正方体按4×4×4的方式堆积而成,共64块。左侧32个方块为235U富集度3%的UO2,右侧为轻水,MCNP模型与此对应。冷却剂流动方向为+y轴方向,入口流速为5 m·s-1。手动输入与程序输入的计算结果符合较好,验证了耦合程序的准确性和可靠性。
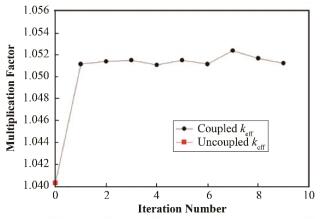
2.2 物理耦合计算结果分析TMSR-SF1堆芯经过耦合计算的有效增值因子keff如图 4所示。从图 4中可以看出,未耦合情况下keff为1.04031,经过一次耦合循环后,有效增殖因子相对于未耦合计算结果有明显变化,增大约1.08%,之后该因子不再随着耦合循环次数增加而变化,在1.051附近波动;耦合后,有效增殖因子明显增大的原因是MCNP输入文件中的材料截面库根据温度反馈更新后,部分位置的实际温度与初始冷态温度相差较大,材料与粒子相互作用的反应截面变化剧烈,最终影响有效增殖因子。而该因子在一定范围内波动的情况,则是由蒙特卡罗方法固有的统计误差造成的。
|
图 4 TMSR-SF1堆芯keff随耦合次数的变化 Figure 4 Difference in keff with the iteration number of TMSR-SF1. |
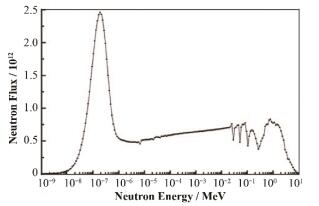
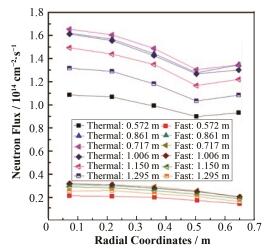
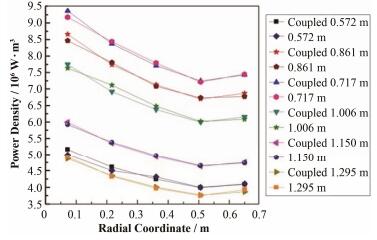
耦合计算后TMSR-SF1堆芯活性区中子能谱如图 5所示,不同轴向高度中子通量密度分布如图 6所示,活性区功率密度分布如图 7所示。堆芯活性区平均功率密度5.19 MW·m-3,未耦合状态下最大功率密度9.17 MW·m-3,耦合状态下最大功率密度9.37 MW·m-3,整个活性区耦合前后功率密度改变量为0.24%-3.31%。从图 6、7中可知,耦合前后不同轴向高度的功率密度与中子通量密度变化趋势相同,堆芯轴向中心部分的中子通量密度最高,在堆芯活性区中部最低,靠近反射层处,因部分中子自反射层返回堆芯,使堆芯边缘功率密度增大。对比相同轴高耦合前后的径向功率密度分布发现,功率密度分布一致,但部分位置功率密度值相差较大的原因是未耦合时MCNP计算使用平均温度,耦合后当部分位置实际温度与平均温度偏差较大时,功率密度值便产生更大变化。
|
图 5 堆芯活性区中子能谱 Figure 5 Neutron spectrum in the active region. |
|
图 6 不同轴向高度中子通量密度分布 Figure 6 Neutron flux density distribution at different axial heights. |
|
图 7 不同轴向高度功率密度分布 Figure 7 Power density distribution at different axial heights. |
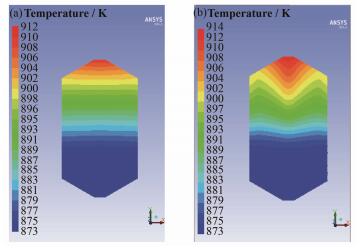
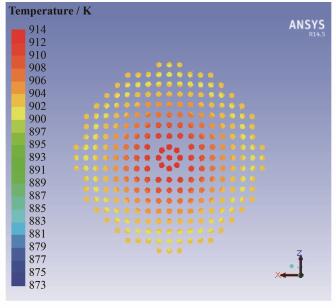
耦合前后堆芯活性区温度分布如图 8所示。由图 8可以看出,熔盐在堆芯活性区中向上流动,在球床下方空腔中温度变化较小,进入球床后被燃料球加热,温度逐渐升高,在顶部区域达到最高,与未耦合情况下堆芯最高温度912.098 K相比,耦合后变为913.793 K,升高1.695 K。图 9为出口孔道温度分布,中心出口孔道温度较高,外侧孔道温度较低。
|
图 8 活性区XY截面温度分布(a)未耦合,(b)耦合 Figure 8 Temperature distribution on XY plane of the core. (a) Not coupled, (b) Coupled |
|
图 9 堆芯出口截面温度分布 Figure 9 Temperature distribution on the exit plane of the core. |
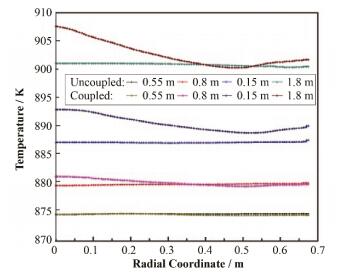
采用耦合计算前后的堆芯径向温度场如图 10所示。从图 10中可以看出,未耦合和耦合计算的径向温度在刚进入球床(0.55 m)处差别较小,但随着冷却剂在堆芯活性区中向上流动,温差逐渐增大,最大温差出现在堆芯中心轴向高度1.5 m处,为7.584 K。两者的温度分布变化趋势和温度值有明显差异,耦合计算的温度变化趋势与功率密度分布一致。
|
图 10 不同轴向高度的温度径向分布 Figure 10 Temperature distribution at different axial heights. |
本文根据现阶段10 MW TMSR-SF1的主要设计参数,建立了该堆型的中子物理及热工水力模型,并通过C++编程语言实现了两个模型间的耦合模拟,编制了用于在MCNP和ANSYS Fluent之间交换堆芯活性区功率密度分布、温度场等数据的耦合程序,并分析了稳态情况下的有效增殖因子、堆芯功率密度分布、温度分布等数据,主要结论如下:
1) TMSR-SF1堆芯在装料高度为130 cm、控制棒完全抽出的情况下,与未耦合时单用MCNP的计算数值相比,耦合后有效增殖因子从1.0403升至1.0515,增大约1.08%,堆芯功率密度改变范围为0.24%-3.31%。
2) 在入口温度为873.15 K、入口平均流速0.2335 m·s-1的情况下,与未耦合时单用Fluent的计算数值相比,耦合后堆芯最高温度由912.098 K升至913.793 K,升高1.695 K,而耦合前后冷却剂最大温差为7.584 K,出现在球床中心轴向高度1.5 m处。
中子物理-热工耦合研究可提供核反应堆运行中更为准确的信息,为研究TMSR-SF1中冷却剂流动状态、温度场、材料性质对反应堆运行的影响、功率密度分布及核燃料燃耗研究提供了重要参考。
| [1] | Ingersoll D T, Forsberg C W, Ott L J, et al. Status of preconceptual design of the advanced high-temperature reactor (AHTR)[M]. United States: Department of Energy, 2004. |
| [2] |
江绵恒, 徐洪杰, 戴志敏. 未来先进核裂变能——TMSR核能系统[J].
中国科学院院刊, 2012, 27(3): 366–374.
JIANG Mianheng, XU Hongjie, DAI Zhimin. Advanced fission energy program-TMSR nuclear energy system[J]. Bulletin of Chinese Academy of Sciences, 2012, 27(3): 366–374. DOI: 10.3969/j.issn.1000-3045.2012.03.016 |
| [3] | Cheng M S, Dai Z M. Development of a three dimension multi-physics code for molten salt fast reactor[J]. Nuclear Science and Techniques, 2014, 25(1): 010601. DOI: 10.13538/j.1001-8042/nst.25.010601 |
| [4] |
薛春, 张海青, 朱智勇, 等. 组件型熔盐堆燃料组件的设计研究[J].
核技术, 2016, 39(9): 090602.
XUE Chun, ZHANG Haiqing, ZHU Zhiyong, et al. Design of fuel assembly for molten-salt-cooled reactors[J]. Nuclear Techniques, 2016, 39(9): 090602. DOI: 10.11889/j.0253-3219.2016.hjs.39.090602 |
| [5] | Kophazi J, Lathouwers D, Kloosterman J L. Development of a three-dimensional time-dependent calculation scheme for molten salt reactors and validation of the measurement data of the molten salt reactor experiment[J]. Nuclear Science and Engineering, 2009, 163(2): 118–131. DOI: 10.13182/NSE163-118 |
| [6] | Zhang Z H, Xia X B, Cai J, et al. Simulation of radiation dose distribution and thermal analysis for the bulk shielding of an optimized molten salt reactor[J]. Nuclear Science and Techniques, 2015, 26(4): 040603. DOI: 10.13538/j.1001-8042/nst.26.040603 |
| [7] | Guo Z P, Wang C L, Zhang D L, et al. The effects of core zoning on optimization of design analysis of molten salt reactor[J]. Nuclear Engineering and Design, 2013, 265: 967–977. DOI: 10.1016/j.nucengdes.2013.09.036 |
| [8] | Guo Z P, Zhou J J, Zhang D L, et al. Coupled neutronics/thermal-hydraulics for analysis of molten salt reactor[J]. Nuclear Engineering and Design, 2013, 258(2): 144–156. DOI: 10.1016/j.nucengdes.2013.01.013 |
| [9] | Zhou J J, Wang C L, An H Z, et al. Three dimensional neutronic/thermal-hydraulic coupled simulation of MSR in steady state condition[J]. Nuclear Engineering and Design, 2014, 267(2): 88–99. DOI: 10.1016/j.nucengdes.2013.11.074 |
| [10] | Li L S, Yuan H M, Wang K. Coupling of RMC and CFX for analysis of Pebble Bed-Advanced High Temperature Reactor core[J]. Nuclear Engineering and Design, 2012, 250: 385–391. DOI: 10.1016/j.nucengdes.2012.05.036 |
| [11] |
何杰, 夏晓彬, 蔡军, 等. 2 MW液态钍基熔盐实验堆主屏蔽温度场分析[J].
核技术, 2016, 39(4): 040601.
HE Jie, XIA Xiaobin, CAI Jun, et al. Temperature field analysis for the main shielding of the 2-MW thorium-based molten salt experimental reactor[J]. Nuclear Techniques, 2016, 39(4): 040601. DOI: 10.11889/j.0253-3219.2016.hjs.39.040601 |
| [12] | Fratoni M, Greenspan E. Neutronic feasibility assessment of liquid salt-cooled pebble bed reactors[J]. Nuclear Science and Engineering, 2011, 168(1): 1–22. DOI: 10.13182/NSE10-38 |
| [13] | Wu C Y, Ferng Y M, Chieng C C, et al. Investigating the advantages and disadvantages of realistic approach and porous approach for closely packed pebbles in CFD simulation[J]. Nuclear Engineering and Design, 2010, 240(5): 1151–1159. DOI: 10.1016/j.nucengdes.2010.01.015 |
| [14] | Vazquez M, Tsige-Tamirat H, Ammirabile L, et al. Coupled neutronics thermal-hydraulics analysis using Monte Carlo and sub-channel codes[J]. Nuclear Engineering and Design, 2012, 250(3): 403–411. DOI: 10.1016/j.nucengdes.2012.06.007 |
| [15] | Conlin J L, Ji W, Lee J C, et al. Pseudo material construct for coupled neutronic-thermal-hydraulic analysis of VHTGR[J]. Transactions of American Nuclear Society, 2005, 92: 225–227. |
| [16] | Hu J, Rizwan-uddin. Coupled neutronics and thermal-hydraulics simulations using MCNP and FLUENT[J]. Transactions of the American Nuclear Society, 2008, 98: 606–608. |




