2. 中国科学院大学 北京 100049;
3. 上海科技大学 上海 201210
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. ShanghaiTech University, Shanghai 201210, China
作为一种新型光源,自由电子激光(Free Electron Laser, FEL)在光致电离激发[1]、分子超快动力学[2]、生物学[3]等诸多领域都有着广泛的应用,这得益于其优良的光学特性。其亮度高、相干性好,所以在物质结构表征成像方面表现出色[4];其脉冲持续时间可以达到飞秒量级,使得我们可以在样品结构破坏之前采集到足够多的样品信息,进行样品结构的图像重建[5]。具体到三维成像方面的应用,在传统的同步辐射光源上,样品的三维成像通过不断改变受照射样品的取向来实现[6],这样做的缺点是样品要接受长时间辐照,辐射损伤大;使用自由电子激光进行成像则能在样品结构破坏之前采集到足够多的样品结构信息,进行结构图像重建。但由于样品照射一次后即被破坏,无法获得更多的三维信息,所以目前的自由电子激光三维成像都只针对特殊样品,如样品有一定的对称性[7],或者样品有很多极为相似的副本[8]。
双光束单脉冲三维成像装置则是一套正在搭建的旨在克服上述不足的装置,目标是实现一般性样品的单脉冲三维成像,这套装置将用于上海软X射线自由电子激光装置。其设计思路是将一个自由电子激光单脉冲一分为二,经过两个不同的光路,从不同角度同时照射样品。在0°-90°范围内,通过增大两光束之间的夹角,有利于获得更多三维结构信息,提高三维成像分辨率,从而通过相干衍射成像技术进行高分辨的三维成像。目前在国际上,这种类似的分束装置常被用来表征光的相干性[9],进行光子关联谱实验[10]或进行傅里叶全息成像实验[11],还没有被用来进行三维相干衍射成像的成功例子。
对于该套装置,关键是保证两束光同时照射到样品上。上海软X射线自由电子激光装置所产生的自由电子激光脉冲是百飞秒级的,这就需要一套高精度的时空对准方案。计划先采用可见光进行离线时空对准,再采用自由电子激光进行在线时空对准。经过计算,采用可见光光源进行离线时空对准,调节精度达2.1 fs,可以满足装置的要求。为了保证离线对准的顺利实现,需要搭建一套基于双光束白光干涉原理的离线对准系统。我们设计了一套双光束白光干涉系统,随后利用MATLAB软件对离线时空对准原理进行了模拟,最后搭建了该套系统。
1 对准原理与双光束白光干涉系统设计图 1为自由电子激光双光束单脉冲三维成像装置设计示意图,其中M1为超环面镜,M2为劈裂镜,R1、R2、L1为反射镜,R1和R2通过电动位移台可在X方向上一起同步运动,光束经M2后一分为二,最终在样品处相交,样品后端放置两个探测器。为了研究此成像装置的时空对准方法,我们搭建了一台离线时空对准系统。该系统进行离线对准的总体思路是:在装置前端先后放置激光和白光光源,样品处放置可见光探测器,然后通过调节R1和R2的位置,并通过探测器上的干涉条纹进行判断,来实现离线时空对准。激光用于空间对准,保证两束光照射到同一位置;白光用于时间对准,保证分出来的两束光同时到达这一位置。
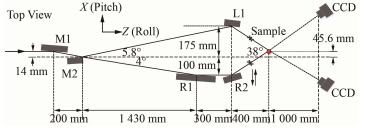
|
图 1 双光束单脉冲三维成像装置设计示意图 Figure 1 Design schematic of double-beam three-dimensional imaging device based on single shot FEL pulse. |
首先采用激光进行空间对准,进行离线时空对准时可以不考虑超环面镜M1,移开M1,激光经M2分束成两路光,上面一路经L1指向样品处,下面一路经R1和R2指向样品处,样品位置处放置可见光探测器。观察样品处探测器,不断调节L1、R1、R2的俯仰角等,直到上下两路光在样品位置处的光斑重合,并观察到干涉条纹。激光具有较窄的线宽,理论上可以认为是单色光。在单色光干涉的情形中,比较经典的杨氏双缝干涉图样的强度函数为余弦的平方,视觉呈现为明暗相间的条纹,激光干涉虽与双缝干涉情形有所不同,但干涉图样依然是明暗相间的条纹,光斑内强度变化的总趋势则服从单光束衍射规律。空间对准的调节除了要保证观察到单色光干涉条纹以外,还要保证平移电动位移台时,可见光探测器上观察到的光斑不随位移台运动而移动,这是时间对准的基础。
随后采用白光进行时间对准,经过前面一步的空间对准调节后,白光分出的两路光在样品处探测器形成的光斑已能较好重合在一起。接着不断调节R1和R2底座下方的电动位移台,使R1和R2同步在X方向上运动,观察样品处探测器,直到中心出现干涉条纹。干涉条纹的中心对应的即是等光程点。光程相等意味着两束光到达样品的时间同步,即时间对准。白光干涉的强度计算中,先计算单色光的干涉强度分布,再把所有单色光进行强度相加。由于每一种波长的光产生的干涉条纹的条纹间距不同,除等光程点处外,其余条纹均有相互位移,这就导致远离等光程点的位置条纹对比度不断下降,然后消失。经过计算,基于双光束白光干涉原理进行的时间对准,调节精度可达2.1 fs,可以满足成像装置的要求。
1.2 双光束白光干涉系统设计基于上述可见光离线对准原理,我们设计了一套双光束白光干涉系统,如图 2所示。可以看到,相比于图 1的在线X光对准系统,双光束白光干涉系统的光路有所改变,两光束最终的夹角从38°变为2°。改变的原因是为了增加干涉条纹的周期,降低对观测探测器的分辨率要求,有利于本系统时空对准调试与验证的进行。离线对准系统的原理、光源和探测器可直接移植到在线对准系统,只需要更换更高倍数的探测器镜头即可。该双光束白光干涉系统用于图 1所示成像装置进行对准时,光束夹角由2°变为38°,干涉条纹间距变为1 μm。利用像素尺寸4 μm的电荷耦合器件(Charge Coupled Device, CCD),结合40倍的光学放大镜头可以观测1 μm的干涉条纹间距。
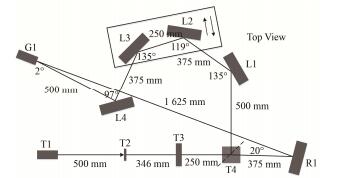
|
图 2 双光束白光干涉系统光路示意图 Figure 2 Light paths schematic of double-beam white light interference system. |
图 2中T1为可见光光源,采用单色光光源时为532 nm的绿光激光,采用白光光源时为白光发光二极管(Light Emitting Diode)。T2和T3配合白光光源使用。T2为狭缝,如上面所述,配合T1使用形成线光源,作为光学系统的“物”,其“像”则为在探测器G1上形成的光斑。实验中所用狭缝可在一定范围内调节狭缝宽度。T3为对白光进行聚集的器件,为凸透镜,其焦距与T2和T3间的光程及T3和G1间的光程相关联。T4为分光棱镜,将光束分为强度近似相等的两束光。L1、L2、L3、L4、R1均为反射镜。L2和L3通过电动位移台可在一个方向上一起同步运动,根据几何关系可以证明,当该运动方向与通过L2和L3之间的光线呈82°的夹角时,经L4反射在G1处形成的光斑不会跟随电机运动而发生移动。G1为探测器,用于观察形成的光斑,可在两个档位上选择观测视野和观测分辨率。以上光学器件都设定在400-700 nm波长工作范围。
2 双光束白光干涉系统的理论模拟基于波动光学原理,利用MATLAB软件进行了双光束白光干涉系统的理论模拟。
2.1 空间对准原理理论模拟图 2中的光源T1采用波长532 nm的绿光激光器,光斑直径为1 mm,挪开狭缝T2和凸透镜T3,激光直接到达T4进行分光。
为简便起见,只计算一维方向上发生干涉的情形,假设激光波前的振幅服从高斯分布,以T1激光出射处为初始计算波前,计算探测器G1处的光强分布。由于激光分成上下两路到达G1,所以采用分别计算出两路光在G1的复振幅,然后再进行复振幅相加并取模的平方的方法计算G1处的光强分布。利用菲涅耳-基尔霍夫衍射公式可得出经反射镜L1、L2这一路到达G1的光线在G1处的复振幅表达式为:
| $ {E_1}(y) = \frac{1}{{i\lambda (l + \Delta l)}}\int\limits_{-t}^t {\frac{1}{{\sqrt {2{\rm{\pi }}} \sigma }}{{\rm{e}}^{-\frac{{y_1^2}}{{2{\sigma ^2}}}}} \cdot {{\rm{e}}^{ik\sqrt {{{(l + \Delta l-y\cos \theta )}^2} + {{({y_1} - y\sin \theta )}^2}} }}} {\rm{d}}{y_1} $ | (1) |
同理可得经R1一路到达G1的光线在G1处的复振幅表达式为:
| $ {E_{\rm{2}}}(y) = \frac{1}{{i\lambda l}}\int\limits_{-t}^t {\frac{1}{{\sqrt {2{\rm{\pi }}} \sigma }}{{\rm{e}}^{-\frac{{y_1^2}}{{2{\sigma ^2}}}}} \cdot {{\rm{e}}^{ik\sqrt {{{(l + y\cos \theta )}^2} + {{({y_1}-y\sin \theta )}^2}} }}} {\rm{d}}{y_1} $ | (2) |
式中:y1为T1初始波前的坐标变量;y为G1处的一维坐标变量;k=2π/λ,λ=532 nm为激光波长;l=3096mm为T1到G1的光程;Δl为L1和L2同步在电机上运动产生的光程变化;t=0.5 mm为激光光束直径的一半,σ=t/3;θ=89°为光在探测器上的入射角。两路光的相干强度,E1(y)+E2(y)的模的平方,即为探测器G1处的光强分布。利用MATLAB计算得到探测器0.12 mm范围内的光强分布曲线(图 3)。可以看到探测器平面存在等强度分布的干涉条纹,条纹间距为15.2μm。
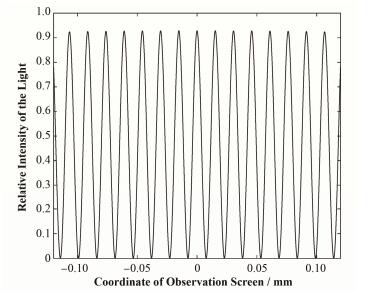
|
图 3 观测点附近光强分布曲线 Figure 3 Light intensity distribution curve around observation point. |
利用白光干涉实现时间对准,光源采用3W的白光LED,狭缝T2和凸透镜T3移入光路,狭缝T2宽度取0.3 mm,T2配合T1使用时作为线光源,是光学系统的“物”,T3对白光起聚集作用,白光经过T2和T3后在T4处分光。
和空间对准的理论模拟类似,计算一维方向上发生干涉的情形,将T1看作点光源,以T2白光出射处为初始波前。将白光分解为若干波长不同的单色光,对于每一个单色光,根据波动光学分别计算两路光在G1的相干光强,然后将所有单色光的结果进行强度相加,即得到白光干涉的强度分布。经过理论模拟,400-700 nm波长范围内取300个波长值可以得到比较理想的理论模拟结果。除此之外,还要考虑白光LED的光谱分布,市面上常见的白光LED灯的白光是靠蓝光LED的蓝光激发黄色荧光粉产生的,据此,将强度服从高斯分布的460 nm蓝光和560 nm黄光按一定比例混合后可得到理论模拟所需的白光光谱,如图 4所示[12]。
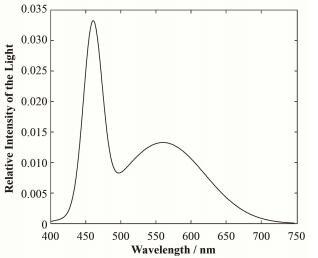
|
图 4 理论模拟所用白光光谱 Figure 4 White light spectrum of theoretical simulation. |
考虑光从T2出射时的倾斜因子和透镜对光波的相位改变,可以得出经反射镜L1、L2这一路到达G1的光线复振幅为:
| $ \begin{align} & {{E}_{1}}(y)=-\frac{1}{\lambda _{\nu }^{2}(l+\Delta l)z}\iint{C\cdot \frac{{{\text{e}}^{i{{k}_{v}}\sqrt{{{x}^{2}}+{{d}^{2}}}}}}{{{x}^{2}}+{{d}^{2}}}\cdot {{\text{e}}^{i{{k}_{v}}\sqrt{{{z}^{2}}+{{(x-{{y}_{1}})}^{2}}}}}\cdot {{\text{e}}^{-i{{k}_{v}}\frac{y_{1}^{2}}{2f}}}\cdot } \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \begin{matrix} {{\text{e}}^{i{{k}_{v}}\sqrt{{{(l+\Delta l-y\text{cos}\theta )}^{2}}+{{({{y}_{1}}-y\text{sin}\theta )}^{2}}}}}\text{d}x\text{d}{{y}_{1}} \\ \end{matrix} \\ \end{align} $ | (3) |
其中:
| $ C = \frac{1}{{\sqrt {2{\rm{\pi }}} {\sigma _1}}}{{\rm{e}}^{ - \frac{{{{({\lambda _\nu } - 4.6 \times {{10}^{ - 4}})}^2}}}{{2\sigma _1^2}}}} + \frac{2}{{\sqrt {2{\rm{\pi }}} {\sigma _2}}}{{\rm{e}}^{ - \frac{{{{({\lambda _\nu } - 5.6 \times {{10}^{ - 4}})}^2}}}{{2\sigma _2^2}}}} $ |
表示不同波长的单色光在白光光谱中的权重。同理可得经R1一路到达G1的光线在G1处的复振幅为:
| $ \begin{gathered} {E_{\text{2}}}(y) =-\frac{1}{{\lambda _\nu ^2lz}}\iint {C \cdot \frac{{{{\text{e}}^{i{k_v}\sqrt {{x^2} + {d^2}} }}}}{{{x^2} + {d^2}}} \cdot {{\text{e}}^{i{k_v}\sqrt {{z^2} + {{(x-{y_1})}^2}} }} \cdot {{\text{e}}^{-i{k_v}\frac{{y_1^2}}{{2f}}}} \cdot } \\ {\text{ }}{{\text{e}}^{i{k_v}\sqrt {{{(l + y\cos \theta )}^2} + {{({y_1} - y\sin \theta )}^2}} }}{\text{d}}x{\text{d}}{y_1} \\ \end{gathered} $ | (4) |
式中:x为狭缝T2处的坐标,积分范围为-0.15-0.15mm;y1为透镜T3处的坐标,积分范围为-2-2 mm;y为G1处的一维坐标;l为T3到G1的光程,为2250 mm;Dl为L1和L2同步在电机上运动产生的光程变化;z为T2到T3的光程,为346mm;d为T1到T2的光程,为500 mm;σ1=1.33×10-5 mm,σ2=6×10-5 mm。
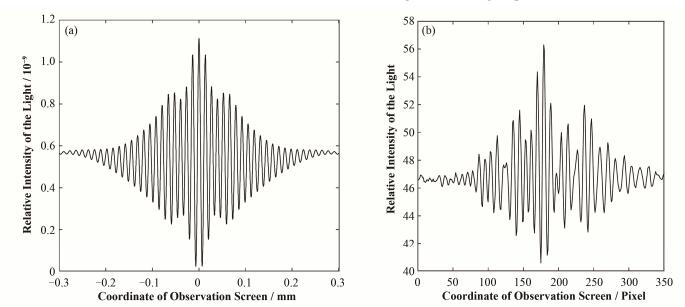
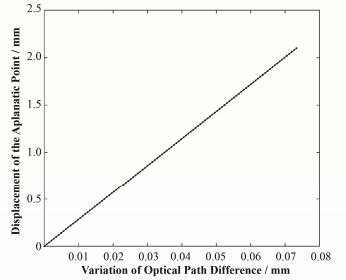
先取Δl=0,计算观测点左右0.3 mm范围内的光强分布曲线,如图 5(a)所示,可以看到条纹对比度从中间往两边逐渐下降。图 6给出了与图 5(a)对应的干涉图样仿真图,中心干涉条纹的间距为13.72mm。取Δl=0.003 mm,发现等光程点发生了移动,表明通过调节L2和L3,可以使等光程点发生移动。时间对准的目的就是使等光程点移动到光斑中心。改变Δl的值,得到等光程点移动量与光程差改变量之间的关系,如图 7所示,二者呈线性关系,斜率约为28.65,即光程差改变1 μm时,等光程点移动28.65 μm。
|
图 5 观测点附近光强分布曲线(a)理论模拟,(b)实验结果 Figure 5 Light intensity distribution curve around observation point. (a) Theoretical simulation, (b) Experimental result |

|
图 6 观测点附近干涉图样仿真图 Figure 6 Interference pattern simulation diagram around observation point. |
|
图 7 等光程点移动量与光程差改变量之间的函数关系 Figure 7 Function relationship between displacement of the aplanatic point and variation of optical path difference. |
单色光源采用俄罗斯Laser-Export公司的LCS-T-11型绿光激光器,工作模式为连续输出,激光波长为532 nm,光斑直径为(0.9±0.2) mm;白光光源采用白光LED灯。T2为狭缝,宽度在0-10mm可调。T3为透镜,采用大恒的GCL-010642型双胶合消色差透镜,直径为40 mm,焦距为300 mm。T4是分光棱镜,选用美国THORLABS公司的CCM1-BS013型非偏振型分束镜。
L1、L2、L3、L4、R1这5个反射镜的直径为50 mm。通过高精度反射镜架对反射镜进行空间姿态调节。采用电控位移台实现L2/L3在x方向的平移,运动行程为±50 mm,运动分辨率为1 μm。运动分辨率的需求是由等光程点移动量与L2/L3运动量之间的关系来决定的。理论模拟得到的等光程点移动量与光程差改变量之间的线性关系系数为28.65,根据光路图可算出光程差改变量与L2/L3的运动量之间的线性关系系数约为0.52。从而得到等光程点移动量与L2/L3的运动量之间的线性关系系数约为14.9。据此选择电机运动分辨率为1 μm。
G1为可见光探测器,由两组光学放大镜头和CCD相机组成,实验过程中可切换观察视野和观察分辨率,大视野观测范围线度为10 mm,小视野观测范围线度为2 mm,分辨率为1.5 μm。所有元件放置在GJ-I型阻尼隔振光学平台。
3.2 双光束白光干涉系统的搭建与调试 3.2.1 空间对准调试依次校准激光器和各反射镜,保证光在各光学器件之间传播时始终平行于光学平台,然后将各光学器件安装到光学平台上。将探测器调到小视野,调节L2/L3电机,观察探测器上的光斑。优化L3的角度,使得L2/L3电机平动时,探测器光斑保持不动,为之后的时间对准做准备。
探测器切换到10 mm大视野,通过调整L4和R1的角度,使L4和R1反射的两个光斑重合在一起,实现空间对准。然后将探测器切换到2 mm小视野,如图 8所示,观察到很多干涉条纹,干涉条纹的宽度约为13.5 μm,理论计算的条纹宽度为15.2mm,两者基本吻合,误差主要来自于手动安装造成的光学元件位置偏差。为了进一步证实条纹来自于双光束的干涉,将其中一束光挡住,发现干涉条纹消失。

|
图 8 小视野下观测到双光束干涉条纹 Figure 8 Double-beam interference fringes observed under narrow field-of-view. |
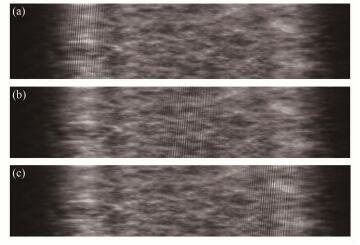
将狭缝T2和透镜T3安装到光学平台上,并调节其位置,使激光从它们中心通过。然后换上白光光源,为了增强其相干性,在白光光源后加一狭缝,并选择尽量小的宽度和适当小的长度。调节L4和R1的角度,使两路白光的光斑重合。然后调节L2/L3电机,在小视野范围中寻找等光程点,得到白光干涉条纹,如图 9所示。图 9(a)-(c)分别对应白光干涉条纹开始进入光斑、到达光斑中心和即将离开光斑三种情形。白光干涉的条纹周期宽度约为13.5μm,理论结果为13.72 μm,两者符合较好。通过电机的位置坐标和白光干涉条纹移动经过的距离可得到等光程点移动的精度:电机每运动1 μm,等光程点移动14.44 μm,与理论计算结果14.9 μm符合较好。根据图 9(b)给出白光干涉条纹附近400个像素元的光强分布曲线,如图 5(b)所示。从图 5中可以看到,实验结果与理论结果符合得较好。
|
图 9 白光干涉条纹在光斑中移动(a)开始进入光斑,(b)到达光斑中心,(c)即将离开光斑 Figure 9 White light interference fringes shifted in the facula. (a) Began to appear, (b) Reached the center, (c) Leaving the facula |
14.44 μm的等光程点移动精度,相当于48.1 fs的时间调节精度。通过改变探测器分辨率(更换光学镜头),双光束白光干涉系统可作为自由电子激光双光束单脉冲三维成像装置的离线对准系统,调节精度达2.1 fs。
4 结语本文基于可见光离线对准原理设计了一套双光束白光干涉系统,并对该系统进行了离线对准原理的理论模拟和实际的时空对准调试实验。利用激光实现了空间对准,利用白光进行双光束白光干涉,观测到白光干涉条纹,实现了时间对准。时间调节精度为48.1 fs,和理论模拟结果符合得很好,通过更改探测器镜头,该系统可用于自由电子激光成像装置的离线时空对准。
| [1] | Feng H, Zhang Y Z, Jiang Y H. Atomic and molecular experiments progress in free-electron laser field[J]. Laser & Optoelectronics Progress, 2016, 53(1): 010002. DOI: 10.3788/LOP53.010002 |
| [2] | Jiang Y H, Rudenko A, Perez-torres J F, et al. Investigating two-photon double ionization of D-2 by XUV-pump-XUV-probe experiments[J]. Physical Review A, 2010, 81(5): 051402. DOI: 10.1103/PhysRevA.81.051402 |
| [3] | Seibert M M, Ekeberg T, Maia F, et al. Single mimivirus particles intercepted and imaged with an X-ray laser[J]. Nature, 2011, 470(7332): 78–81. DOI: 10.1038/nature09748 |
| [4] | Barty A, Boutet S, Bogan M J, et al. Ultrafast single-shot diffraction imaging of nanoscale dynamics[J]. Nature Photonics, 2008, 2(7): 415–419. DOI: 10.1038/nphoton.2008.128 |
| [5] | Capotondi F, Pedersoli E, Bencivenga F, et al. Multipurpose end-station for coherent diffraction imaging and scattering at FERMI@Elettra free-electron laser facility[J]. Journal of Synchrotron Radiation, 2015, 22(3): 544–552. DOI: 10.1107/S1600577515004919 |
| [6] | Miao J, Sandberg R L, Song C. Coherent X-ray diffraction imaging[J]. IEEE Journal of Selected Topics in Quantum Electronics, 2012, 18(1): 399–410. DOI: 10.1109/jstqe.2011.2157306 |
| [7] | Xu R, Jiang H, Song C, et al. Single-shot three-dimensional structure determination of nanocrystals with femtosecond X-ray free-electron laser pulses[J]. Nature Communications, 2014, 5: 1–9. DOI: 10.1038/ncomms5061 |
| [8] | Kassemeyer S, Steinbrener J, Lomb L, et al. Femtosecond free-electron laser X-ray diffraction data sets for algorithm development[J]. Optics Express, 2012, 20(4): 4149–4158. DOI: 10.1364/oe.20.004149 |
| [9] | Singer A, Sorgenfrei F, Mancuso A P, et al. Spatial and temporal coherence properties of single free-electron laser pulses[J]. Optics Express, 2012, 20(16): 17480–95. DOI: 10.1364/oe.20.017480 |
| [10] | Grübel G, Stephenson G B, Gutt C, et al. XPCS at the European X-ray free electron laser facility[J]. Nuclear Instruments and Methods in Physics Research Section B:Beam Interactions with Materials and Atoms, 2007, 262(2): 357–367. DOI: 10.1016/j.nimb.2007.05.015 |
| [11] | Günther C M, Pfau B, Mitzner R, et al. Sequential femtosecond X-ray imaging[J]. Nature Photonics, 2011, 5(2): 99–102. DOI: 10.1038/nphoton.2010.287 |
| [12] |
方福波, 王垚浩, 宋代辉, 等. 白光LED衰减的光谱分析[J].
发光学报, 2008, 29(2): 353–357.
FANG Fubo, WANG Yaohao, SONG Daihui, et al. Spectroscopic analysis of white LED attenuation[J]. Chinese Journal of Luminescence, 2008, 29(2): 353–357. |


