2. 中国科学院近代物理研究所 兰州 730000;
3. 中国科学院宁波材料技术与工程研究所 宁波 315201
2. Institute of Modern Physics, Chinese Academy of Sciences, Lanzhou 730000, China;
3. Ningbo Institute of Materials Technology and Engineering, Chinese Academy of Sciences, Ningbo 315201, China
随着我国工业化程度的逐步深化,目前的能源消耗总量和二氧化碳排放总量已经位居全球第一[1]。我国以煤炭为主的能源结构客观造成了阻碍工业健康发展的环境污染问题。而解决经济发展和环境冲突的重要手段是开发清洁能源,其中,核能源是目前公认的重要选项。核能源应用的关键问题在于反应堆系统的安全性,这一点从根本上取决于核能材料的本征物理性能。因此,核材料的结构和性质的研究显得至关重要。
常见的核燃料一般指含有235U、233U、239Pu可裂变核素的单质、合金或化合物,238U和232Th是可以通过中子轰击产生可裂变核素的物质。以含铀核燃料为例,其化学形式包括:1) 金属铀燃料:它的密度较高,易加工且有较高的热导率,在25 C为25 W·m−1·K−1[2]。2) 氧化铀系核燃料:该类型核燃料包括UO2、钚铀氧化物混合燃料(Mixed uranium and plutonium oxide fuel, MOX)等,它们能工作在较高温度下,密度比金属类型的核燃料低,但它们硬度不高易脆化,热导率过低。其中UO2在720 C时其热导率只有3.5W·m−1·K−1[3],这就会导致其服役时堆芯温度过高。3) 铀硅系列核燃料:包含了准化学计量比的U3Si、U3Si2、U5Si4、USi、USi3、USi2和非化学计量比的USi1.88和U3Si5(USi1.67)。其中U3Si有着超高的U密度(14.7g·cm−3)和较高的热导率(30W·m−1·K−1 (720 C))被认为是具有潜力的新型核燃料,但是U3Si在服役时的过度肿胀却成为其一个重要缺点。4) 氮化铀系燃料:其中UN化学稳定性好,有着较高熔点(2850 C),其热导率约为20W·m−1·K−1 (720 C),可被用于第四代快堆[4]。5) 碳化铀系列核燃料:包含了准化学计量比的UC、UC2和U2C3,其中UC作为第四代反应堆核燃料,相比传统核燃料有着显著的优点。UC拥有极高的硬度,其熔点高达2380 C,并且在较宽的温度范围内不会有相转变,因而可承受较高的服役温度,其热导率高达23 W·m−1·K−1 (720 C),密度为13.63kg·m−3。其也可以很好地同钚和部分锕系元素组成三元体系混合使用[5]。而在高温反应堆中,UC2经常作为UO2的还原剂与UO2一起混合使用。此外,还有氟化铀熔盐、钍基熔盐和硫酸铀酰的水溶液等其他形式[6]。图 1给出了部分核燃料热导率随温度的变化情况,可以发现作为先进核燃料的碳化铀在热导率方面有着显著的优势[7]。
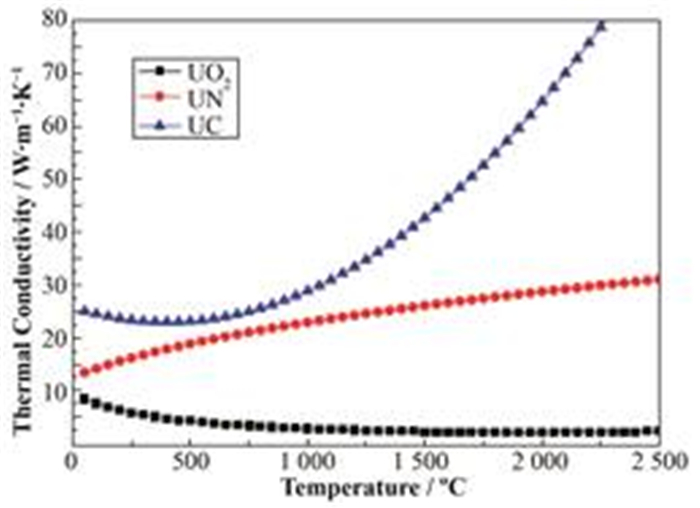
|
图 1 不同燃料的热导率 Figure 1 Thermal conductivities of different fuel options. |
在核燃料的服役过程中,燃料基体中会产生各种缺陷和裂变产物,这会对燃料的热导率和力学性能产生重要的影响。研究缺陷和裂变产物的行为是核燃料科学中的一个重要课题,通常可采用对核燃料进行辐照(Irradiation)实验观察燃料基体的变化情况,而理论上则常采用第一性原理(First-principles)等计算方法来研究裂变产物的稳定性及扩散现象。本文将回顾近年来碳化铀核燃料领域的研究进展,重点关注缺陷对于核燃料结构和稳定性的影响。下面我们将通过实例从不同角度详细说明。
1 铀碳化合物的制备及基本物理性质目前比较常用的制备碳化铀的方法是在高温下用碳还原二氧化铀,然后经破碎、球磨、制粒、压制和烧结等过程便可以制备出碳化铀。因其方法比较简便经济而且原材料容易获得,所以比较适用于大规模工业生产[8]。Reiche等[9]在1400 C通过中子衍射的方法,用UO2和石墨粉末通过反应UO2+ 2C→UC+CO2制备出了碳化铀。他们发现,当温度超过1500 C时,C原子会通过扩散进入UC的八面体间隙位而形成C2团簇,从而局部形成立方结构的β-UC2相。Raveu等[10]指出,要制备纯度较高的UC需尽量保持在低氧低湿度的条件下以避免UC被氧化,在UC的烧结过程中纯氩气保护能进一步降低样品表面的含氧量,但UC样品经常会含有少量的UC2,而这些UC2在有氧条件下会被首先氧化。郭航旭等[11]采用溶胶凝胶法制备碳化铀小球,与其它方法相比该方法制备的碳化铀小球能够产生更多的能量而且克服了放射性气溶胶和不易包壳等难题。其采用欠酸的硝酸铀酰(Acid Deficient Uranyl Nitrate, ADUN)提供铀酰离子,尿素作为金属络合剂防止UO22+过早沉淀及提高其浓度。其主要原理如下:
| $ \begin{align} & 2\text{CO}{{\left( \text{N}{{\text{H}}_{2}} \right)}_{2}}+\text{ U}{{\text{O}}_{2}}^{2+}\Leftrightarrow \text{U}{{\text{O}}_{2}}{{\left[\text{CO}{{\left( \text{N}{{\text{H}}_{2}} \right)}_{2}} \right]}_{2}}^{2+}; \\ & \text{U}{{\text{O}}_{2}}^{2+}+2{{\text{H}}_{2}}\text{O}\to \text{U}{{\text{O}}_{2}}{{\left( \text{OH} \right)}_{2}}+2{{\text{H}}^{+}}; \\ & {{\left( \text{C}{{\text{H}}_{2}} \right)}_{6}}{{\text{N}}_{4}}+4{{\text{H}}^{+}}+6{{\text{H}}_{2}}\text{O}\to 4\text{N}{{\text{H}}_{4}}^{+}+6\text{HCHO}; \\ & \text{U}{{\text{O}}_{2}}{{\left( \text{OH} \right)}_{2}}\to \text{U}{{\text{O}}_{3}}\cdot {{\text{H}}_{2}}\text{O}\to \text{U}{{\text{O}}_{3}}+{{\text{H}}_{2}}\text{O}; \\ & \text{U}{{\text{O}}_{3}}+{{\text{H}}_{2}}\to \text{U}{{\text{O}}_{2}}+{{\text{H}}_{2}}\text{O}; \\ & \text{U}{{\text{O}}_{2}}\xrightarrow{c}\text{UCO}\xrightarrow{c}\text{U}{{\text{C}}_{2}}。\\ \end{align} $ |
Tagawa等[12]在1400 C左右通过反应7UC2+ UO2→4U2C3+2CO制备出了U2C3,同时UC会作为中间产物产生。Hansen等[13]发现U2C3在1780 C会发生如下分解反应:U2C3→UC+UC2,同时伴随着较大的体积变化。Inoue等[14]发现U2C3受到高剂量的中子辐照后会转变为UC1.5(UC+UC2),并认为可能的原因是辐照急剧加强了C在U2C3中的扩散。Elliott等[15]发现在1800 C时会发生共析反应:β-UC2↔UC+α-UC2。
低温下碳在铀中的溶解度很低:在α-U中小于3×10−6,在β-U中小于10−5,在γ-U中为0.07%− 0.09%,但碳的溶解度会随着温度而增加。在1200−2500 C之间,碳在液体铀中溶解度可以表示为[16]:
| $ \begin{align} & \ln \left( \frac{C}{U} \right)=68.129-5.292\ 2\frac{{{10}^{5}}}{T}+1.534\ 7\frac{{{10}^{9}}}{{{T}^{2}}}- \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 1.972\ 1\frac{{{10}^{12}}}{{{T}^{3}}}+9.279\ 1\frac{{{10}^{14}}}{{{T}^{4}}} \\ \end{align} $ | (1) |
铀碳化合物数据可由实验观测直接获得。Raj等[17]测得U2C3和UC2的密度分别为12.88 kg·m−3和11.68 kg·m−3,可见相对于UO2(密度和含铀密度分别为10.96 g·cm−3、9.67 g·cm−3)碳化铀系列都有着较高的密度和铀元素核密度,另测得UC2和U2C3熔点分别为2450 C和1820 C。Holleck等[18]发现UC在温度−271.95 C以上无超导现象,室温下UC的电阻率ρ=(0.34±0.02) μΩ·cm,且电阻率会随着空位、间隙缺陷的出现而增大。Eloirdi等[19]在实验上测得了低温下U2C3的电阻率随温度的变化情况,并归纳了其电阻率在−253 C以下时服从数学表达形式ρ=(83+0.4T2) μΩ·cm。
光谱是检测碳化铀结构和成分的重要手段,Bober等[20]用球面反射计和不同波长及入射角的偏振光研究了液体UC的光学性质。当入射光波长为458 nm和514 nm时,液态UC的折射率(Refractive indexing,n)为2,当波长为647 nm时n为2.5,以上几种波长下UC的折射率会随着温度的升高而轻微下降,但当入射波长为752 nm时其折射率为1.7,此时折射率与温度无关。液态UC的吸收常数(Absorption constant,κ)也有类似的规律,当入射光波长为458 nm和514 nm时κ为2.5,当波长为647nm时其值为3.1,且吸收常数随着温度升高而降低,当波长为752 nm时κ为2.5且与温度无关。同时Bober等[20]研究了多晶UC的光谱发射率(Spectral emissivity,ε),并归纳了在波长为650 nm处的发射率随温度的变化规律为(25−2500 C)[20]:
| $ \begin{align} & {{\varepsilon }_{650}}=0.566-2.720\ 9\times {{10}^{-6}}T+2.769\ 7\times {{10}^{-9}}{{T}^{2}}- \\ & \ \ \ \ \ \ \ \ \ \ \ 2.710\ 2\times {{10}^{-12}}{{T}^{3}}+2.861\ 7\times {{10}^{-16}}{{T}^{4}} \\ \end{align} $ | (2) |
当温度为2500−4000 C时,液体UC在波长为650 nm处的光谱发射率ε为:
| $ \begin{align} & {{\varepsilon }_{650}}=0.452-4.324\ 7\times {{10}^{-6}}\left( T-2\ 780 \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ 3.196\ 7\times {{10}^{-9}}{{\left( T-2\ 780 \right)}^{2}}- \\ & \ \ \ \ \ \ \ \ \ \ \ 1.678\ 4\times {{10}^{-12}}{{\left( T-2\ 780 \right)}^{3}}- \\ & \ \ \ \ \ \ \ \ \ \ \ 4.664\ 1\times {{10}^{-16}}{{\left( T-2\ 780 \right)}^{4}} \\ \end{align} $ | (3) |
在实际应用时我们可以认为在波长为650 nm处固体UC (25 C)光谱发射率ε650为0.55,而液态的UC (2 700 C)的发射率ε650为0.45。De等[21]认为固体和液体UC的ε(波长在488−900 nm之间)与波长的关系可以归纳为:
固体UC:
| $ {{\varepsilon }_{\lambda }}=0.757\ 46-0.467\ 91\lambda +0.184\ 90{{\lambda }^{2}} $ | (4) |
液体UC:
| $ {{\varepsilon }_{\lambda }}=0.799\ 98-0.755\ 45\lambda +0.390\ 36{{\lambda }^{2}} $ | (5) |
Grossman等[22]研究了UC2的光学性质,得出α-UC2在温度区间为1000−2100 C时其全波长半球发射率为0.55。
2 铀碳化合物的热学性质Okamoto[23]和Benz等[24]分别得出了U-C体系的热力学相图,Okamoto的结果如图 2所示。Preusser等[25]在725 C时获得UC、UC2和U2C3的热容Cp分别是64.02 J·K−1·mol−1、83.6 J·K−1·mol−1、142.3J·K−1·mol−1。Holley等[26]得到UC、UC1.9和UC1.94的德拜温度θD分别为55 C、31 C和31 C,同时归纳了在室温25−1800 C时固体UC的热容Cp (J·K−1·mol−1)以及吉布斯自由能(J·mol−1)随温度变化情况(25 C以上)如下:
| $ \begin{align} & {{C}_{\text{p}}}\left( \text{UC}, \text{Solid} \right)=50.124+2.57\times {{10}^{-2}}-1.868\times {{10}^{-5}}{{T}^{2}}+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 5.716\times {{10}^{-9}}{{T}^{3}}-6.187\times {{10}^{5}}{{T}^{-2}} \\ \end{align} $ | (6) |
| $ \begin{align} & {{\Delta }_{\text{f}}}G{}^\circ \left( \text{UC}, \text{Solid} \right)=-31\ 465.6-499.228T+64.750\ 1T\ln T- \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {7\ 984\ 166}/{T}\;-0.014\ 4{{T}^{2}} \\ \end{align} $ | (7) |
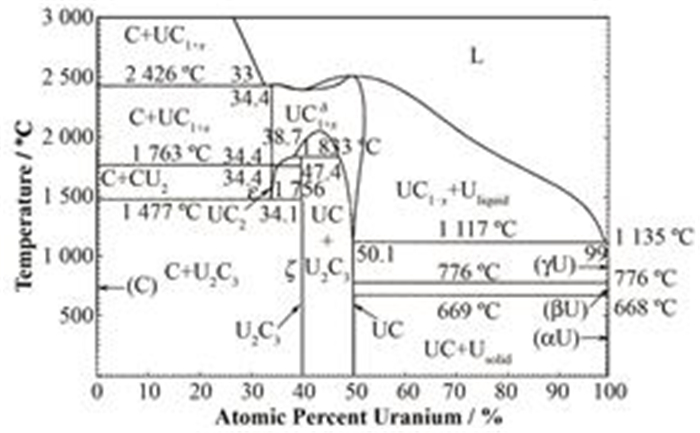
|
图 2 碳化铀体系的热力学相图 Figure 2 Phase diagram of U-C system. |
通过表达式可以计算得出碳化铀的热容会随着温度升高而缓慢增加,同时可以得到在室温下UC的吉布斯自由能为−98.89 kJ·mol−1。另外表 1列出了其他几组不同实验测得碳化铀体系在室温下(25 C)的生成焓和熵。Sheth等[27]则归纳了融化态的UC的热容Cp (J·K−1·mol−1)以及ΔH° (J·mol−1)随温度的变化情况:
| $ {{C}_{\text{p}}}\left( \text{UC}, \text{Liquid} \right)=49.887+7.794\times {{10}^{-3}}T $ | (8) |
| $ H{}^\circ \left( T \right)-H{}^\circ \left( 298 \right)=51\ 362+49\ 887T+3.987\times {{10}^{-3}}{{T}^{2}} $ | (9) |
| 表 1 室温下实验测得碳化铀系列化合物的生成焓和熵的比较 Table 1 Comparison of the experimental U-C enthalpy of formation and entropy at room temperature. |
由式(8) 可知,熔融态UC在2700 C时的热容Cp为73.269 J·K−1·mol−1。
3 铀碳化合物的微观结构、力学性质及氧化行为立方晶系的UC拥有与NaCl同样的构型,其空间群为Fm3m,Olsen等[29]发现在高压下(27 GPa)立方晶系的UC会转变为正交晶系。UC能够以次化学计量比和超化学计量比的形式存在,前者是由于基体中存在空位,后者是由C−C双原子取代了原来的单原子C。UC2拥有两种同分异构体:四方晶系CaC2构型的α-UC2(空间群为I4/mmm)和立方晶系CaF2构型的β-UC2(空间群为Fm3m)。Chang等[30]发现α-UC2在1 800 C将会转变为β-UC2,说明β-UC2为UC2的高温形态。UC2中容易产生一系列的C空位缺陷,故其常以次化学计量比UC2−x的形式存在[28]。图 3为铀碳系列化合物的晶体结构模型,其中:大个球体为U原子,小个球体为C原子。Chevalier等[31]在实验上发现α-UC2和UC可以在1500 C以上共同存在,立方晶系Pu2C3构型的U2C3则只能存在于1800 C以下,另外U2C3中不容易产生本征缺陷,故很容易保持准化学计量比。
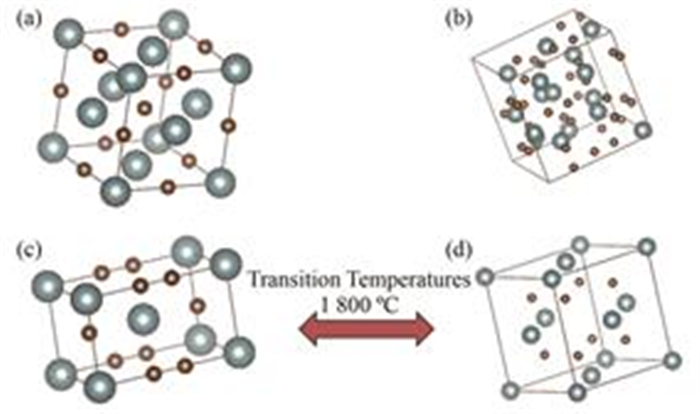
|
图 3 晶体结构模型(a) UC,(b) U2C3,(c) α-UC2,(d) β-UC2 Figure 3 Crystal structures of U-C compounds. (a) UC, (b) U2C3, (c) α-UC2, (d) β-UC2 |
Shi等[32−33]计算了铀碳化合物的电子结构与能带,指出UC在费米面附近,有大量的能带穿过,表现出明显的金属性。费米能级附近能带的主要来源是U原子的5f轨道,其分布从−1.2−3.4 eV。α-UC2和UC有类似的金属特征,U的5f轨道贡献分布在−4−2 eV之间。同样,U2C3也具有本征的导体属性。对于碳化铀的化学键,UC中U−C键长为0.248 nm;α-UC2中U−C键长分别为0.233 nm和0.259 nm;U2C3中U−C键长分别为0.250 nm、0.256 nm和0.282nm。α-UC2中的C−C共价键长为0.1377 nm,而U2C3中C−C键长为0.1438 nm,更接近于石墨中的C−C键长(0.142 nm)[19, 34]。Chartier等[35]用分子力学下的嵌入原子作用势(Embedded atom method potential)得到在UC中C−C共价键长为0.1368nm。Eloirdi等[19]指出在U2C3中C−C键和C−U键的作用要弱于其他几种铀碳化合物并认为这是导致U2C3的热不稳定性和高温分解(U2C3在1840 C以上会分解为UC和β-UC2)的原因,但长度为0.334 nm的U-U金属键强度则要强于其它几种化合物。由于核燃料工作在高温环境下,因此有必要研究气相态的碳化铀。UC2在温度范围为2100−2400 C内可以固气共存,同时在2200 C以上UC分子还会通过反应UC2(g)+U(g)=2UC(g)出现。另一些实验通过质谱分析法发现了UC3分子的存在。Wang等[36]根据不同分子构型的生成焓对碳化铀分子可能的结构做了理论推测,图 4分别为UC2分子的线性和三角构型、UC3分子的“T”型和扇形构型[35]。
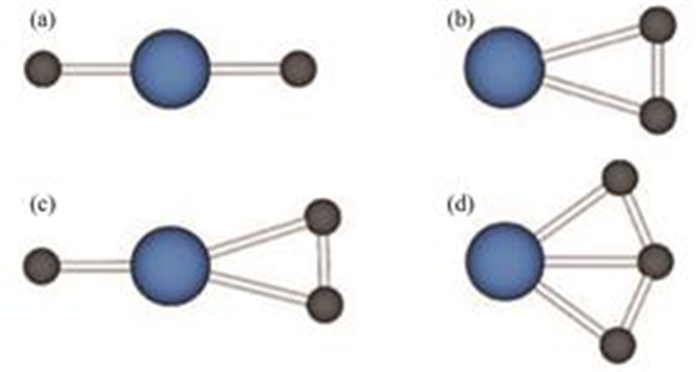
|
图 4 理论上UC (n=2−3) 可能的分子结构(a)线性-UC2,(b)三角-UC2,(c) “T”型-UC3,(d)扇形-UC3 Figure 4 Structures of UC (n=2−3) molecular species levels of theory. (a) Linear-UC2, (b) Trigonal-UC2, (c) "T"-UC3, (d) Fan-UC3 |
针对碳化铀的力学性质,人们也从实验和理论两个角度做了深入的研究。对于立方晶系的UC、四方晶系的α-UC2以及立方晶系的U2C3分别有3、6、3个独立的弹性常数,从弹性常数可以推断出晶体的剪切模量和体模量等。Austin[34]和Sandenaw等[37]在实验上得出铀碳化合物的晶格常数和体模量。Matzke[38]在106 Pa下得出UC的杨氏模量、剪切模量、体模量和泊松比分别是210 GPa、81.3 GPa、167.8 GPa和0.291。Routbort等[39]测量了UCx (0.9 < x < 1.03) 的弹性常数,并发现随着x剪切模量增大,其原因可能是碳原子的增多其电子对金属键的贡献增加,从而增强了键能。Tokar[40]和Chang等[30]发现UC的硬度随着温度的升高而降低,但是大于相同条件下的UN;UC的屈服强度不仅与温度有关还与C/U的比例有关,UC1+x的屈服强度远大于次化学计量比的UC1−x和准化学计量比的UC;UC1−x的蠕变速率要快于UC1+x。另外在UC中掺入杂质可以改变蠕变速率,例如掺入Zr可以减缓蠕变速率,掺入Ni则会加速蠕变。可见,化学成分的变化可以深刻影响碳化铀的力学性能[41]。表 2列出碳化铀系列的弹性常数的实验值和理论值。Yamamoto[42]和Freyss等[43]采用第一性原理的方法计算了不同铀碳化合物的晶格常数和体模量。Ducher[44]和Shi等[32−33]考虑到锕系5f电子强关联效应使用了DFT+U的方法对其进行了修正,此外Shi等[33]得出了UC、α-UC2和U2C3的泊松比ν分别为0.32、0.30和0.28,呈现出典型的金属属性(典型金属的泊松比范围0.25 < ν < 0.45)。表 3为不同文献采用不同方法的计算结果,可以看出在引入Hubbard项后,理论计算的晶格常数能很好符合实验值,但是以上这些文献在计算体模量时都与实验值有一定的偏差。
| 表 2 计算和实验方法所得的弹性常数 Table 2 Calculated and experimental (25 C) elastic constants (GPa). |
| 表 3 计算和实验方法所得的晶格常数和体模量 Table 3 Data of lattice constants and bulk modulus by theoretical and experimental methods. |
此外,UC易于被氧化,刚切开的UC内部呈现带金属光泽的亮灰色,由于氧化作用将很快变暗[20]。Raveu等[10]在制备UC样品时发现表面有大量的氧原子,其中有样品在距表面100 nm左右氧原子浓度超过了30%,同时氧原子浓度还与C/U的计量比有关。Eckle等[45]通过光电子发射光谱,发现UC样品在低氧环境下就能够形成UC-UO的结构即UOxC1−x,在高氧环境下O则能够取代C形成UO2薄膜。Freyss等[43]通过计算证实,在UC基体中O极易停留在间隙和碳空位上,从而形成固溶体,这从理论上解释了UC易氧化的原因。然而,目前对于铀碳化合物氧化反应机理的研究还比较有限,亟待从理论上深入探讨。笔者推荐采用多尺度理论研究方法,从多个时空尺度明晰相关反应动力学过程。
4 辐照产生的点缺陷随着燃耗的加深,核燃料会产生各种点缺陷(如碳空位、铀的弗兰克尔缺陷),这些缺陷会捕获裂变产物,产生局部晶格弛豫现象,并通过聚集影响核燃料服役行为。Eyre等[46]用中子在130 C对碳化铀进行辐照实验,当裂变产物数密度达到1.4×1016cm−3时会产生大量可观测的空位和间隙团簇,并且团簇的数量和大小会随着辐照剂量而增加。在700 C对其进行退火处理,这些空位和间隙会相互结合,从而导致缺陷团簇消失。辐照会导致燃料的力学性能发生改变,这对于理解燃料的服役行为至关重要。例如,Brucklacher等[47]发现在相同的辐照条件下UC的蠕变速率小于UO2,说明UC在辐照条件下能更好地保持其力学稳定性。同时在1000 C左右反应堆内的UC蠕变速率要比反应堆外的蠕变速率高出两个数量级。当停止辐照后,受辐照的样品和没有受辐照的样品的蠕变速率大体相同。Brucklacher等[47]认为辐照下蠕变速率加快可归因于辐照环境导致的晶格缺陷,这些缺陷在高温和辐照下加速扩散导致蠕变速率的加快。
一般用点缺陷形成能(Formation energy)来描述缺陷形成的难易程度,常用的点缺陷形成能公式为:
| $ E_{{{V}_{x}}{{I}_{x}}}^{F}=E_{{{V}_{x}}{{I}_{x}}}^{N\pm 1}-{{E}^{N}}+{{E}_{x}} $ | (10) |
式中:
Chartier等[35]用嵌入原子作用势计算了UC部分缺陷的形成能,得到U的弗兰克缺陷形成能为6.8eV,并估算U空位的形成能约为3.4 eV。Freyss等[43]则通过第一性原理计算了常见点缺陷的形成能,发现其中C空位的形成能最低,即核燃料在辐照条件下很容易通过形成一系列的C空位而形成非化学计量比的UC1−x,空位缺陷会引起晶格体积的轻微缩小,U间隙缺陷则会引起燃料晶格的膨胀且造成的体积变化最大。Ducher等[44]在计算缺陷形成能时考虑了由于辐照引起的非化学计量比带来的影响,对传统的形成能计算方法进行了修正,其表达式如下:
| $ \Delta E_{\text{def}}^{F}=\Delta E_{0}^{F}-{{E}_{\text{d}}}{{E}_{d}} $ | (11) |
式中:Ed为缺陷的形成能;Xd表示该缺陷的浓度;
| 表 4 UC中不同缺陷的形成能 Table 4 Formation energies of different point defects in UC. |
服役环境下,UC中不断产生各种结构缺陷,为U原子和C原子在UC晶体中的自扩散行为提供了条件。这些原子或离子的扩散与燃料的蠕变、晶粒长大以及稠化密切相关,所以了解原子在燃料中的扩散现象对厘清碳化铀的服役行为有极其重要的意义。通常描述扩散过程的物理量为扩散系数D,扩散系数越大表明扩散速率越大,扩散现象也就越明显,在实验上,常用示踪原子法来研究原子的扩散过程。H h等[50]在900 C利用1.17×1014 cm−2·s−1的中子通量(Neutron flux)对UC进行辐照实验,发现辐照可以加快U的扩散速率且远超过温度对扩散系数的影响,得出U在UC中的扩散系数约为2.2×10−17cm2·s−1。Tetenbaum等[51]发现U的扩散系数还与C/U的比例系数有关,在0.9−1.1这个区间内系数越小则U的扩散速率越大,其原因可能是出现更多的C空位,系数越大则扩散的越慢则是因为出现了UC2和U2C3等新的相,较致密的结构和更多的C−U键降低了U的扩散能力。由Arrhenius公式可以得出原子的扩散系数,其表达式为:
| $ D={{D}_{0}}\left[\exp \left(-\frac{{{E}_{\text{a}}}}{KT} \right) \right] $ | (12) |
Matzke等[38]归纳出准化学计量比UC基体中U和C的原子扩散Arrhenius表达式:
| $ D_{\text{UC}}^{\text{U}}=6.9\left[\exp \left(-\frac{141\ 000}{KT} \right) \right] $ | (13) |
| $ D_{\text{UC}}^{\text{C}}=75\left[\exp \left(-\frac{84\ 000}{KT} \right) \right] $ | (14) |
从Matzke等的表达式可以看出C原子的扩散系数远大U原子。
以上提到的这些扩散都是体扩散(Volume diffusion),但是影响燃料性能的不仅只有体扩散还有晶界扩散(Grain-boundary diffusion)和表面扩散(Surface diffusion)等其他形式,这些扩散过程同样与温度、C/U的比例有关。Routbort等[52]对碳化铀中通过晶界和表面的扩散现象进行了研究,发现在1500 C时U原子在次化学计量比UC0.93的晶界中的扩散系数约是UC晶界中的10倍。表 5列出了在不同温度下不同粒子经不同方式的扩散系数,从表 5可以看出,C的体扩散系数比U高出6−9个数量级,U原子在UC的晶界处扩散得最快且比通过体内扩散高出7−8个数量级,其次是通过表面扩散,也比体扩散高6个数量级。在UC基体内通过体扩散的方式是最慢的,另外随着温度的升高扩散系数迅速增大。
| 表 5 铀和碳在UC中经不同扩散方法的扩散系数 Table 5 Diffusivities for uranium and carbon in UC for various processes. |
由Arrhenius公式可知,活化能Ea越小,则扩散系数越大。Schüle等[48]发现在低温( < 1400 C)时C原子是通过最近邻空位来扩散的,在高温( > 1400 C)时则通过碳原子双空位来进行扩散。C和U原子的活化能分别为(1.45±0.30) eV和2.2 eV,进一步说明体积较小的C原子扩散活性更高。Matsui等[53]在820 C时测得U的活化能为(2.1±0.5) eV,与Schüle等的结果符合得很好。而Matzke等[54]利用233U作为标记测得1400−2200 C时U在UC2的活化能为(5.7±0.2) eV,远高于UC中的U,说明U在UC2中的扩散速度较慢。而活化能又可以通过如下表达式获得[55]:
| $ {{E}_{\text{a}}}={{E}^{\text{f}}}+{{E}^{\text{m}}} $ | (15) |
式中:Ef为缺陷的形成能;Em为所求扩散原子的迁移能。Ducher等[44]通过第一性原理计算了C和U的迁移能,它们的迁移能分别为1.6 eV和1.8 eV,并发现在UC中C和U分别是通过最近邻的C空位和U空位来进行扩散的。Bévillon等[55]在此基础上计算了它们的活化能,C和U原子的活化能分别为2.6eV和4.6 eV。虽然理论计算目前难以精确重复实验观测数值,但无论实验上还是理论都有C所需要的活化能比U小,说明C原子的确更容易在UC基体中扩散,可归因于C原子较小的原子体积。
6 碳化铀燃料的裂变产物随着燃耗的加深,UC晶体中裂变产物会逐渐增多,常见的裂变产物有Kr、Ba、Cs、Xe、Zr和I等[56]。此外作为填充气和衰变产物的He的扩散也极其重要。这些裂变/衰变产物会引起燃料的肿胀,随着各种产物密度的增加其肿胀现象也越加明显,同时温度的增加也会加剧肿胀的程度。Harrison等[57]发现UC在700 C裂变产物数密度为1×1021cm−3时,其体积肿胀约为4.8%,在裂变产物数密度为1.5×1021cm−3时,其体积肿胀约7.5%,相比较而言,其肿胀程度略大于UO2,而同样作为核燃料的U3Si,在裂变产物数密度为1×1021cm−3时,其体积肿胀超过12%[58]。
人们描述杂质在一个缺陷位上的稳定性时通常采用形成能(Incorporation energy),即从无穷远处把一个杂质放入一个先前已经存在的缺陷所需要的能量,其表达式为:
| $ {{E}_{\text{inc}}}=E_{x}^{N+1}+{{E}^{N}}-{{E}_{x}} $ | (16) |
式中:Einc为杂质的形成能;
| 表 6 UC中不同杂质的形成能 Table 6 Incorporation energies of different impurities in UC. |
由于裂变产物原子通常趋于占据U空位,所以这里以U空位缺陷作为代表来讨论不同燃料基体中不同裂变产物的稳定情况。这里我们对不同文献的数据进行了总结,图 5给出了来自不同文献中[59−60]裂变产物在U取代位上的形成能。从图 5中可以看出,UO2这条裂变产物形成能曲线在UC曲线的下方(I除外),说明裂变产物在UO2这种基体中更加稳定,而目前可知的U3Si这几个裂变产物的形成能都要高于UO2和UC。可以初步推断,裂变产物在不同基体的稳定性规律是UO2 > UC > U3Si。虽然影响燃料肿胀的机理十分复杂,但可以从形成能的角度初步解释实验上测得燃料肿胀程度从大到小依次为U3Si > UC > UO2。
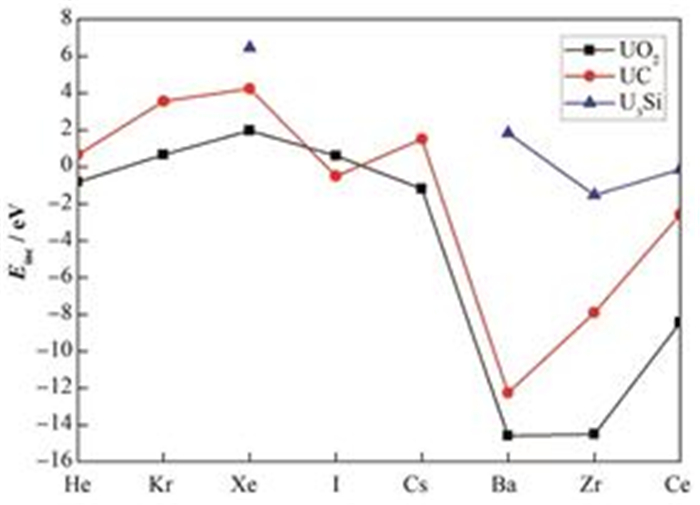
|
图 5 裂变产物在不同基体中铀取代位上的形成能 Figure 5 Incorporation energies of the fission products in the U site of different matrices. |
裂变产物在核燃料内的产生、迁移和聚集等行为会改变核燃料的结构并最终影响核反应堆的安全运行。Matthews[61]研究了裂变气泡在UC和UN中的动力学问题,发现气泡在UC中扩散更快。Felix等[62]在实验上测得1700 C时Kr在UC中的扩散速率约是Xe的3 000倍。为了进一步厘清裂变产物的扩散过程,Matzke等[63]研究了Xe在UC晶格中的扩散过程,并测得Xe的活化能约为3.6 eV。Zumwalt等[64]研究了裂变产物从UC2基体中的释放问题,他们把样品置于均匀的中子辐照强度下,并对辐照后的样品进行了退火处理,得出Xe和Kr扩散的Arrhenius表达式分别为:
| $ D_{\text{U}{{\text{C}}_{2}}}^{\text{Xe}}=4.6\times {{10}^{-6}}\left[\exp \left(-\frac{68\ 000}{KT} \right) \right] $ | (17) |
| $ D_{\text{U}{{\text{C}}_{2}}}^{\text{Kr}}=6.2\times {{10}^{-5}}\left[\exp \left(-\frac{44\ 000}{KT} \right) \right] $ | (18) |
表 7列出了温度范围在700−1700 C时不同裂变产物在不同基体中对应Arrhenius式(12) 的扩散常数,从表 7中可以看出,在UC2基体中Kr的扩散系数大于Xe,这与UC基体中相同。
| 表 7 碳化铀和氧化铀中裂变产物的扩散常数(700−1700 C) Table 7 Constants for fission products diffusion in uranium carbides and uranium dioxide (700−1700 C). |
Bévillon等[55]计算了多种裂变产物在碳化铀内的扩散活化能,得出稀有气体的扩散活化能比过渡金属和稀土元素要低,这与之前计算的裂变产物在缺陷位的稳定性有相似的规律。在不同碳铀化学计量下,各种元素的扩散活化能也不尽相同,比如Xe在次化学计量比UC1−x的活化能为3.8 eV,而在准化学计量比的UC中的活化能为2.9 eV,在超化学计量比UC1+x中为3.0 eV。另外稀有气体I、Cs、Ba扩散活化能随着原子体积而增加。稀有气体需要的活化能相比于其他元素较少,说明在相同的条件下,稀有气体容易扩散聚集从而形成裂变气泡导致燃料的肿胀,并对燃料的热力学性能和结构稳定性造成影响。
7 结语本文简要介绍了碳化铀系列化合物的制备方法、结构、物理性质,以及辐照下缺陷的形成和演化机制,并推荐利用多尺度计算方法对铀碳化合物的氧化行为进行深入的理论研究。我们期望通过本篇综述可以帮助人们加深对于铀碳化合物的认识,进一步推动对碳化铀系列核燃料的研究工作。
| [1] |
宋杰鲲. 我国二氧化碳排放量的影响因素及减排对策分析[J].
价格理论与实践, 2010, 30(1): 37–38.
SONG Jiekun. The influence factors of carbon dioxide emissions of our country and the analysis of reducing countermeasures[J]. Theory and Practice, 2010, 30(1): 37–38. |
| [2] | Yamasaki S. Evaluation of thermal conductivity of hyperstoichiometric UO2+x by molecular dynamics simulation[J]. International Journal of Thermophysics, 2007, 28(2): 661–673. DOI: 10.1007/s10765-007-0170-6 |
| [3] | Inoue M. Thermal conductivity of uranium-plutonium oxide fuel for fast reactors[J]. Journal of Nuclear Materials, 2000, 282(2-3): 186–195. DOI: 10.1016/S0022-3115(00)00407-4 |
| [4] | Szpunar B, Szpunar J A. Thermal conductivity of uranium nitride and carbide[J]. International Journal of Nuclear Energy, 2014, 71(1): 152–159. DOI: 10.1155/2014/178360 |
| [5] | Vigier N, Den Auwer C, Fillaux C, et al. New data on the structure of uranium monocarbide[J]. Chemistry of Materials, 2008, 20(9): 3199–3204. DOI: 10.1021/cm8001783 |
| [6] |
仇婷婷, 彭佳, 何淑华, 等. 稀土氟化物在硝酸中溶解性质的研究[J].
核技术, 2015, 38(11): 110304.
QIU Tingting, PENG Jia, HE Shuhua, et al. Solubility of rare earth fluorides in nitric acid[J]. Nuclear Techniques, 2015, 38(11): 110304. DOI: 10.11889/j.0253-3219.2015.hjs.38.110304 |
| [7] | Zhao H, Zhu D, Chaudri K S, et al. Preliminary transient thermal-hydraulic analysis for new coated UN and UC fuel options in SCWR[J]. Progress in Nuclear Energy, 2014, 71(1): 152–159. DOI: 10.1016/j.pnucene.2013.11.008 |
| [8] |
孙吉昌, 宋殿武, 杨有清. 碳化铀的制备和分析[J].
中国核科技报告, 1987, 2(0): 646–655.
SUN Jichang, SONG Dianwu, YANG Youqing. Preparation and analysis of uranium carbides[J]. China Nuclear Science and Technology Report, 1987, 2(0): 646–655. |
| [9] | Reiche M H, Vogel S C. In situ synthesis and characterization of uranium carbide using high[J]. Journal of Nuclear Materials, 2016, 471(1): 308–316. DOI: 10.1016/j.jnucmat.2015.12.044 |
| [10] | Raveu G. Experimental study of UC polycrystals in the prospect of improving the as-fabricated sample purity[J]. Nuclear Instruments and Methods in Physics Research B, 2014, 314(1): 72–76. DOI: 10.1016/j.nimb.2014.09.007 |
| [11] |
郭航旭, 李飒, 秦芝. 溶胶凝胶法制备碳化铀小球[C]. 第三届全囯核化学与放射化学青年学术研讨会, 南宁, 2015.
GUO Hangxu, LI Sa, QIN Zhi. Preparation of uranium carbide pellets by sol-gel method[C]. 3rd National Youth Academic Symposiums on Nuclear and Radiochemistry, Nanning, 2015. |
| [12] | Tagawa H, Fujii K. Formation of U2C3 in the reaction of UC2 with UO2[J]. Journal of Nuclear Materials, 1971, 39(1): 109–114. DOI: 10.1016/0022-3115(71)90189-9 |
| [13] | Hansen M, Anderko K, Salzberg H W. Constitution of binary alloys[J]. Journal of the Electrochemical Society, 1958, 105(12): 260C–261C. DOI: 10.1149/1.2428700 |
| [14] | Inoue T, Horiki M, Matsui H, et al. Deposition of U2C3 in neutron irradiated UC+UC2[J]. Journal of Nuclear Materials, 1978, 71(2): 372–374. DOI: 10.1016/0022-3115(78)90438-5 |
| [15] | Elliott R P. McGraw-hill series in materials science and engineering[M]. New York: McGraw Hill, 1965. |
| [16] | Storms E K. Uranium-carbon and plutonium-carbon systems[R]. Los Alamos: Los Alamos Scientific Laboratory, 1969. DOI: 10.2172/4815047. |
| [17] | Raj B, Vijayalakshmi M, Rao P R V, et al. Challenges in materials research for sustainable nuclear energy[J]. Materials Research Society Bulletin, 2008, 33(4): 327–337. DOI: 10.1557/mrs2008.67 |
| [18] | Holleck H, Kleykamp H. Gmelin handbook of inorganic chemistry[G]. Berlin: Springer-Verlag, 1987. |
| [19] | Eloirdi R, Fuchs A J, Griveau J C, et al. Evidence for persistent spin fluctuations in uranium sesquicarbide[J]. Physical Review B, 2013, 87(21): 214414. DOI: 10.1103/PhysRevB.87.214414 |
| [20] | Bober M, Singer J, Wagner K. Bestimmung der optischen konstanten von geschmolzenen kernbrennstoffen[J]. Journal of Nuclear Materials, 1984, 124(1): 120–128. DOI: 10.1016/0022-3115(84)90016-3 |
| [21] | De Coninck R, Van Lierde W, Gijs A. Uranium carbide: thermal diffusivity, thermal conductivity and spectral emissivity at high temperatures[J]. Journal of Nuclear Materials, 1975, 57(1): 69–76. DOI: 10.1016/0022-3115(75)90179-8 |
| [22] | Grossman L N. High-temperature thermophysical properties of uranium monocarbide[J]. Journal of the American Ceramic Society, 1963, 46(6): 264–267. DOI: 10.1111/j.1151-2916.1963.tb11723.x |
| [23] | Okamoto H. CU (carbon-uranium)[J]. Journal of Phase Equilibria and Diffusion, 2005, 26(6): 642–642. DOI: 10.1007/s11669-005-0016-5 |
| [24] | Benz R, Hoffman C G, Rupert G N. Some phase equilibria in the thorium-nitrogen system[J]. Journal of the American Chemical Society, 1967, 89(2): 191–197. DOI: 10.1021/ja00978a001 |
| [25] | Preusser T. Modeling of carbide fuel rods[J]. Nuclear Technology, 1982, 57(3): 343–371. |
| [26] | Holley C, Rand M H, Storms E K. The chemical thermodynamics of actinide elements and compounds Part 6: the actinide carbides[M]. Vienna: Intl Atomic Energy Agency, 1985. |
| [27] | Sheth A, Tetenbaum M, Leibowitz L. Vapor pressures of UC and (U0. 8Pu0. 2)C at extremely high temperatures[J]. Transactions of the American Nuclear Society, 1975(22): 271–275. |
| [28] | Rand M H. Thermodynamics of nuclear materials[J]. Atomic Energy Review, 1975, 13(1): 145–151. |
| [29] | Olsen J S, Gerward L, Benedict U, et al. High-pressure structural studies of UC by v-ray diffraction and synchrotron radiation[J]. Journal of the Less Common Metals, 1986, 121: 445–453. DOI: 10.1016/0022-5088(86)90561-8 |
| [30] | Chang R. A diffusionless UC2 (cubic) to UC2 (tetragonal) transformation[J]. Acta Crystallographica, 1961, 14(10): 1097–1098. DOI: 10.1107/S0365110X61003223 |
| [31] | Chevalier P Y, Fischer E. Thermodynamic modelling of the C-U and B-U binary systems[J]. Journal of Nuclear Materials, 2001, 288(2): 100–129. DOI: 10.1016/S0022-3115(00)00713-3 |
| [32] | Shi H L, Zhang P. Electronic structures and mechanical properties of uranium monocarbide form first-principles LDA+U and GGA+U calculations[J]. Physics Letters A, 2009, 373(39): 3577–3581. DOI: 10.1016/j.physleta.2009.07.074 |
| [33] | Shi H L, Zhang P, Li S. First-principles study of UC2 and U2C3[J]. Journal of Nuclear Materials, 2010, 369(2): 218–222. DOI: 10.1016/j.jnucmat.2009.11.009 |
| [34] | Austin A E. Carbon positions in uranium carbides[J]. Acta Crystallographica, 1959, 12(2): 159–161. DOI: 10.1107/S0365110X59000445 |
| [35] | Chartier A, Van Brutzel L. Modeling of point defects and rare gas incorporation in uranium mono-carbide[J]. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 2007, 255(1): 146–150. DOI: 10.1016/j.nimb.2006.11.017 |
| [36] | Wang X, Andrews L, Ma D, et al. Infrared spectra and quantum chemical calculations of the uranium-carbon molecules UC, CUC, UCH, and U(CC)2[J]. Journal of Chemical Physics, 2011, 134(24): 244313. DOI: 10.1021/ja102475t |
| [37] | Sandenaw T A. Evidence for order-disorder in PuC0. 80 at low temperatures through specific-heat measurements[J]. Journal of Nuclear Materials, 1975, 57(2): 145–150. DOI: 10.1016/0022-3115(75)90254-8 |
| [38] | Matzke H. Science of advanced LMFBR fuels: a monograph on solid state physics, chemistry and technology of carbides, nitrides and carbonitrides of uranium and plutonium[M]. Amsterdam: North Holland, 1986. |
| [39] | Routbort J L. Adiabatic elastic constants of uranium monocarbide[J]. Journal of Nuclear Materials, 1971, 40(1): 17–26. DOI: 10.1016/0022-3115(71)90112-7 |
| [40] | Tokar M. Compressive creep and hot hardness of U-Pu carbides[J]. Journal of the American Ceramic Society, 1973, 56(4): 173–177. DOI: 10.1111/j.1151-2916.1973.tb12448.x |
| [41] | Seltzer M S, Wright T R, Moak D P. Creep behavior of uranium carbide-based alloys[J]. Journal of the American Ceramic Society, 1975, 58(3-4): 138–142. DOI: 10.1111/j.1151-2916.1975.tb19577.x |
| [42] | Yamamoto E, Haga Y, Inada Y, et al. De Haas-van alphen effect and Fermi surfaces in UC[J]. Journal of the Physical Society of Japan, 1999, 68(12): 3953–3959. DOI: 10.1143/JPSJ.68.3953 |
| [43] | Freyss M. First-principles study of uranium carbide: accommodation of point defects and of helium, xenon, and oxygen impurities[J]. Physical Review B, 2010, 81(1): 014101. DOI: 10.1103/PhysRevB.81.014101 |
| [44] | Ducher R, Dubourg R, Barrachin M. First-principles study of defect behavior in irradiated uranium monocarbide[J]. Physical Review B, 2011, 83(10): 104107. DOI: 10.1103/PhysRevB.83.104107 |
| [45] | Eckle M, Gouder T. Photoemission study of UNxOy and UxCy in thin films[J]. Journal of Alloys and Compounds, 2004, 374(1): 261–264. DOI: 10.1016/j.jallcom.2003.11.121 |
| [46] | Eyre B L, Sole M J. On the formation and behaviour of point defect clusters in neutron irradiated uranium carbide[J]. Journal of Nuclear Materials, 1966, 18(3): 314–322. DOI: 10.1016/0022-3115(66)90172-3 |
| [47] | Brucklacher D, Dienst W. Creep behavior of ceramic nuclear fuels under neutron irradiation[J]. Journal of Nuclear Materials, 1972, 42(3): 285–296. DOI: 10.1016/0022-3115(72)90079-7 |
| [48] | Schüle W, Spindler P. Properties of vacancies in uranium carbide[J]. Journal of Nuclear Materials, 1969, 32(1): 20–29. DOI: 10.1016/0022-3115(69)90138-X |
| [49] | Matsui H, Horiki M, Kirihara T. Irradiation of uranium carbides in JMTR[J]. Journal of Nuclear Science and Technology, 1981, 18(12): 922–929. DOI: 10.3327/jnst.18.922 |
| [50] | Höh A, Matzke H. Fission-enhanced self-diffusion of uranium in UO2 and UC[J]. Journal of Nuclear Materials, 1973, 48(2): 157–164. DOI: 10.1016/0022-3115(73)90150-5 |
| [51] | Tetenbaum M, Hunt P D. High-temperature thermodynamic properties of hypo-and hyper-stoichiometric uranium carbides[J]. Journal of Nuclear Materials, 1971, 40(1): 104–112. DOI: 10.1016/0022-3115(71)90121-8 |
| [52] | Routbort J L, Matzke H. Grain-boundary diffusion of U in pure and doped uranium carbides with different C/U ratios[J]. Journal of the American Ceramic Society, 1975, 58(3-4): 81–84. DOI: 10.1111/j.1151-2916.1975.tb19561.x |
| [53] | Matsui H, Kato T, Yagi K, et al. Quenched-in vacancies in single crystalline uranium monocarbide (UC)[J]. Radiation Effects and Defects in Solids, 1989, 108(1): 115–124. DOI: 10.1080/10420158908217874 |
| [54] | Matzke H, Politis C. Self-diffusion of uranium in uranium dicarbide UC2[J]. Solid State Communications, 1973, 12(5): 401–404. DOI: 10.1016/0038-1098(73)90782-5 |
| [55] | Bévillon E, Ducher R, Barrachin M, et al. Investigation of the diffusion of atomic fission products in UC by density functional calculations[J]. Journal of Nuclear Materials, 2013, 434(1): 240–247. DOI: 10.1016/j.jnucmat.2012.11.030 |
| [56] | Song F L, Yang X W, Li X L, et al. The behavior of cesium adsorption on zirconyl pyrophosphate[J]. Nuclear Science and Techniques, 2016, 27(3): 60. DOI: 10.1007/s41365-016-0054-1 |
| [57] | Harrison J W. The irradiation-induced swelling of uranium carbide[J]. Journal of Nuclear Materials, 1969, 30(3): 319–323. DOI: 10.1016/0022-3115(69)90248-7 |
| [58] | Finlay M R, Hofman G L, Snelgrove J L. Irradiation behaviour of uranium silicide compounds[J]. Journal of Nuclear Materials, 2004, 325(2): 118–128. DOI: 10.1016/j.jnucmat.2003.11.009 |
| [59] | Bévillon E, Ducher R, Barrachin M. First-principles study of the stability of fission products in uranium monocarbide[J]. Journal of Nuclear Materials, 2012, 426(1): 189–197. DOI: 10.1016/j.jnucmat.2012.03.014 |
| [60] | Middleburgh S C, Burr P A, King D J M, et al. Structural stability and fission product behaviour in U3Si[J]. Journal of Nuclear Materials, 2015, 466(1): 739–744. DOI: 10.1016/j.jnucmat.2015.04.052 |
| [61] | Matthews C. Fission gas bubble behavior in uranium carbide[D]. Oregon State: Oregon State University, 2015. |
| [62] | Felix F W, Seelig H. New experimental possibilities in the study of diffusion of noble gases in fissionable material[J]. Nukleonik, 1967, 9(1): 389–392. |
| [63] | Matzke H. Application of "channeling" techniques to fission gas release studies[J]. Journal of Nuclear Materials, 1969, 30(1-2): 110–121. DOI: 10.1016/0022-3115(69)90173-1 |
| [64] | Zumwalt L R, Gethard P E, Anderson E E. Fission-product release from monogranular UC2 particles[J]. Nuclear Science and Engineering, 1965, 21(1): 1–12. |
| [65] | Shaked H. Diffusion of xenon in uranium monocarbide[D]. California: University of California, 1962. DOI: 10.2172/4694056. |


