2. 中国科学院大学 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
球床式氟盐冷却高温堆(Pebble Bed Fluoride-salt Cooled High Temperature Reactor, PB-FHR)采用球形燃料元件及液态氟化盐冷却剂,是一种先进的第四代反应堆,能够在高温、低压的工况下运行,具有良好的安全及经济特性[1]。目前世界上已有若干科研机构对PB-FHR做出了相关的研究。德国代尔夫特理工大学于2005年提出了一种球床熔盐堆的概念设计[2];美国伯克利大学于2014年提出了一种小型模块化PB-FHR的概念设计[3];中国科学院上海应用物理研究所于2011年提出了一种PB-FHR小型实验堆设计[4]。
PB-FHR堆芯是一种典型的多孔介质,球形燃料元件随机堆积在PB-FHR的堆芯内,形成了充满空隙的球床区域,冷却剂通过球床的空隙流出堆芯。堆芯热工水力程序是反应堆设计及安全分析的重要工具,用于计算堆芯流场及温度信息,为中子物理模拟提供温度反馈。然而PB-FHR目前并没有专用的堆芯热工水力程序,若干研究机构通过对现有的热工水力程序进行二次开发,使其能够用于PB-FHR。代尔夫特理工大学对高温气冷堆的二维热工水力分析程序THERMIX进行了二次开发并应用于PB-FHR[2]。伯克利大学将熔盐物性植入系统分析程序RELAP中,用于PB-FHR的系统热工水力分析[5]。中国科学院上海应用物理研究所使用商用计算流体力学软件FLUENT建立PB-FHR堆芯多孔介质模型,利用软件提供的二次开发接口添加熔盐物性及换热公式,进行了PB-FHR三维堆芯热工水力分析[6]。西安交通大学采用商用计算流体力学软件ANSYS对PB-FHR球床中的燃料球进行精细建模及模拟,分析了熔盐在球床孔隙及燃料球表面的热工水力特性[7−8]。堆芯燃料球的精确建模及模拟能够提供最详细的热工水力信息,但需使用大量的网格对模型进行划分,导致求解非常耗时。因此,球床堆的全堆芯三维热工水力模拟通常采用多孔介质模型,而球床精确建模方法更适用于堆芯的局部分析。与二维计算程序及系统分析程序相比,三维热工水力程序能模拟具有复杂空间效应的工况,如堆芯功率分布非对称等情况,但计算耗时仍然较高,尤其在耦合中子物理程序及瞬态计算的情况。
从2006年英伟达公司推出CUDA (Compute Unified Device Architecture)运算架构开始,图形处理器(Graphics Processing Unit, GPU)逐步成为了大规模并行数值计算的重要硬件工具[9]。GPU具有大量的计算单元,将可并行的计算任务加载到GPU,可有效提高程序的计算速度。CUDA提供了GPU的硬件接口,为开发者提供了通用的GPU计算模型,有效推动了GPU加速技术在流体力学、材料科学、核科学等科研领域的应用。例如,Bailey等[10]使用GPU将模拟流场的格子玻尔兹曼模拟算法加速了28倍,Boyd等[11]使用GPU将中子输运程序OpenMOC加速了25−35倍。
为PB-FHR研发专用、高效的三维堆芯热工水力程序能有效推动PB-FHR的研究及设计工作。本文将以计算流体力学方法为基础,针对PB-FHR的热工水力特性,研发GPU加速的堆芯热工水力程序(GPU-accelerated Thermal Hydraulic Code, GATH)。本文采用非热平衡多孔介质模型[12]建立堆芯固体结构及冷却剂的物理模型;采用SIMPLEC (Semi-implicit Method for Pressure Linked Equation-Consistent)算法[13]求解流场及压力场;为更准确地模拟球床内流体的热弥散现象,引入多孔介质的湍流模型;为了在大规模网格情况下高速求解堆芯热工水力问题,基于krylov子空间迭代算法及方程预处理算法,研究并实现了GPU高速求解算法;通过对PB-FHR堆芯模型进行热工水力分析,并与商用计算流体力学软件ANSYS CFX的计算结果进行对比,验证程序的正确性,同时详细分析GPU的加速性能。
1 数理模型本文以非热平衡多孔介质模型为基础,将堆芯球床复杂的几何近似为均匀的固相和液相介质。固相介质代表堆芯中的燃料球、反射层等固体结构,液相介质代表熔盐冷却剂。
1.1 冷却剂数理模型冷却剂数理模型包括宏观质量、动量、湍流动能、耗散率及能量守恒方程。
熔盐冷却剂被作为不可压缩流体处理,其质量守恒方程如下:
| $ \nabla \cdot \left( \phi {{\rho }_{\text{f}}}u \right)=0 $ | (1) |
式中:ϕ是多孔介质孔隙率(液相体积分数);ρf是熔盐密度;u为熔盐的物理速度。
流体的流速通过求解宏观动量守恒方程获得。该方程由微观雷诺平均方程进行体积平均化而获得[14]。方程中包含由固相引起的阻力源项,具体表达式如下:
| $ \begin{align} & \phi {{\rho }_{\text{f}}}\frac{\partial {{u}_{\text{i}}}}{\partial t}+\frac{\partial }{\partial {{x}_{\text{j}}}}\left( \phi {{\rho }_{\text{f}}}{{u}_{\text{i}}}{{u}_{\text{j}}} \right)=\frac{\partial }{\partial {{x}_{\text{i}}}}\left( \phi \rho +\frac{2}{3}\phi {{\rho }_{\text{f}}}k \right)+ \\ & \ \ \ \ \ \ \ \ \frac{\partial }{\partial {{x}_{\text{j}}}}\left[\left. \mu +{{\mu }_{\text{t}}} \right)\left( {{S}_{\text{ij}}}+{{S}_{\text{ji}}} \right) \right]-\phi {{R}_{\text{i}}}-\phi {{\rho }_{\text{f}}}{{g}_{\text{i}}} \\ \end{align} $ | (2) |
其中:
| $ {{S}_{\text{ij}}}=\frac{1}{2}\left( \frac{\partial {{u}_{\text{i}}}}{\partial {{x}_{\text{j}}}}+\frac{\partial {{u}_{\text{j}}}}{\partial {{x}_{\text{i}}}} \right) $ | (3) |
式中:Sij为宏观雷诺应力;ui、Ri、gi为i方向的速度、阻力源项、重力加速度;p、μ、k、μt代表压力、速度、宏观湍流动能、湍流粘度;μt的表达式和普通流体相同:
| $ {{\mu }_{\text{t}}}={{\rho }_{\text{f}}}{{c}_{\mu }}\frac{{{k}^{2}}}{\varepsilon } $ | (4) |
式中:cμ为与湍流模型有关的无量纲数,一般取0.09;ε为湍流耗散率。k、ε和μt只在湍流区域存在,通过求解宏观湍流动能及耗散率方程获得。Ri表达式采用了填充床中广泛使用的Ergun公式[15]。
采用局部非热平衡的多孔介质模型,固相和液相的能量方程被分别建立,通过附加的对流换热项耦合[16]。液相的温度(能量)方程表达式如下:
| $ \begin{align} & \phi {{\rho }_{\text{f}}}{{c}_{\text{pf}}}\frac{\partial {{T}_{\text{f}}}}{\partial t}+{{\rho }_{\text{f}}}{{c}_{\text{pf}}}\nabla \cdot \left( \phi u{{T}_{\text{f}}} \right)= \\ & \ \ \ \ \ \nabla \cdot \left[\left. {{\lambda }_{\text{f}, \text{eff}}}\nabla {{T}_{\text{f}}} \right) \right]+ha\left( {{T}_{\text{s}}}-{{T}_{\text{f}}} \right) \\ \end{align} $ | (5) |
式中:cpf、Tf、λf, eff及h代表比热容、温度、有效导热系数及对流换热系数;a为燃料球表面积体积比。λf, eff包含流体固有热导率和湍流热弥散效应产生的导热,本文采用Kuwahara等[17]提出的等效热导率公式。
对流换热项ha(Ts−Tf)代表流体从固体获得的能量,本文采用Wakao[18]提出的对流换热系数的经验公式,该经验公式在填充床中广泛地应用。
流体的等效粘度及等效导热系数需根据湍流动能及耗散率获得,因此采用了N-K多孔介质湍流模型[14],多位研究人员证实该模型的结果适用于球型多孔介质[19],其表达式如下:
| $ \begin{align} & \phi {{\rho }_{\text{f}}}\frac{\partial k}{\partial t}+\frac{\partial }{\partial {{x}_{\text{j}}}}\left( \phi {{\rho }_{\text{f}}}{{u}_{\text{j}}}k \right)=\frac{\partial }{\partial {{x}_{\text{j}}}}\left[\left( \mu +\frac{{{\mu }_{\text{t}}}}{{{\sigma }_{k}}} \right)\frac{\partial \phi k}{\partial {{x}_{\text{j}}}} \right]+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 2\phi {{\mu }_{\text{t}}}{{S}_{\text{ij}}}{{S}_{\text{ij}}}-\phi {{\rho }_{\text{f}}}\varepsilon +\phi {{\rho }_{\text{f}}}{{S}_{k}} \\ \end{align} $ | (6) |
| $ \begin{align} & \phi {{\rho }_{\text{f}}}\frac{\partial \varepsilon }{\partial t}+\frac{\partial }{\partial {{x}_{\text{j}}}}\left( \phi {{\rho }_{\text{f}}}{{u}_{\text{j}}}\varepsilon \right)=\frac{\partial }{\partial {{x}_{\text{j}}}}\left[\left( \mu +\frac{{{\mu }_{\text{t}}}}{{{\sigma }_{\varepsilon }}} \right)\frac{\partial \phi \varepsilon }{\partial {{x}_{\text{j}}}} \right]+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \phi \left( 2{{c}_{1}}{{\mu }_{\text{t}}}{{S}_{\text{ij}}}{{S}_{\text{ij}}}-{{c}_{2}}{{\rho }_{\text{f}}}\varepsilon \right)\frac{\varepsilon }{k}+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \phi {{\rho }_{\text{f}}}{{S}_{\varepsilon }} \\ \end{align} $ | (7) |
式中:Sk及Sε为N-K模型中的湍流动能及耗散率生成率;c1、c2、σk和σε为湍流模型的无量纲常数。
1.2 堆芯固体数理模型堆芯固体(球床、反射层等)的能量守恒方程为宏观导热方程,燃料被当做固定在堆芯内近似处理。堆芯内固体的温度通过求解该方程获得,其表达式如下:
| $ \begin{align} & \left( 1-\phi \right){{\rho }_{\text{s}}}{{c}_{\text{ps}}}\frac{\partial {{T}_{\text{s}}}}{\partial t}=\nabla \cdot \left( {{\lambda }_{\text{s}, \text{eff}}}\nabla {{T}_{\text{s}}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{q}_{\text{n}}}-ha\left( {{T}_{\text{s}}}-{{T}_{\text{f}}} \right) \\ \end{align} $ | (8) |
式中:ρs、cps、Ts、λs, eff代表固体的密度、比热容、温度及有效等效热导率;qn为裂变产生的热功率密度。方程中的对流换热项是冷却剂与燃料球、反射层换热产生的冷却功率密度。
其中,球床的等效导热系数由Zehner-Bauer-Schlünder公式[20]给出,该公式在球床反应堆中广泛应用。该公式考虑到所有传热机制:
| $ {{\lambda }_{\text{s}, \text{eff}}}={{\lambda }_{\text{s}, \text{cont}}}+{{\lambda }_{\text{s}, \text{f}}}+{{\lambda }_{\text{s}, \text{rad}}} $ | (9) |
式中:λs, cont为燃料球的接触导热;λs, f为空隙中滞止的流体导热;λs, rad为球之间的辐射换热等效热导。
2 数值计算方法 2.1 离散方法堆芯热工水力物理量的控制方程(流场、温度场等)可以表示成广义的偏微分方程形式:
| $ \phi \rho \frac{\partial \psi }{\partial t}+\rho \nabla \cdot \left( \rho u\psi \right)=\nabla \left[\left. \mathit{\Gamma }\cdot \nabla \psi \right) \right]+S $ | (10) |
式中:ψ为待求物理量(流场或温度场);Γ为广义扩散系数;S为广义源项。通用控制方程由瞬时项、对流项、扩散项及源项组成。
采用有限体积法将偏微分方程在三维圆柱坐标系的规则网格下进行空间离散,采用交错网格存储网格面上的流速。对流项采用一阶迎风格式,瞬时项采用一阶向后差分格式。对通用控制方程进行空间及时间上的积分后,便获得离散方程:
| $ \begin{align} & {{a}_{\text{P}}}{{\psi }_{\text{P}}}={{a}_{\text{E}}}{{\psi }_{\text{E}}}+{{a}_{\text{W}}}{{\psi }_{\text{W}}}+{{a}_{\text{N}}}{{\psi }_{\text{N}}}+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ {{a}_{\text{S}}}{{\psi }_{\text{S}}}+{{a}_{\text{F}}}{{\psi }_{\text{F}}}+{{a}_{\text{B}}}{{\psi }_{\text{B}}}+b \\ \end{align} $ | (11) |
式中:aP、aE、aW、aN、aS、aF、aB分别为网格中心、东侧、西侧、北侧、南侧、前侧、后侧的待求变量的离散系数;b为与源项有关的系数。三维空间网格的所有离散方程形成了一个大型七对角矩阵的线性方程组,需使用线性方程组的迭代求解算法计算方程组的解。
2.2 SIMPLEC算法宏观动量方程是压力与速度耦合的方程,采用SIMPLEC算法对其求解。SIMPLEC算法首先假设初始的压力分布,求解动量方程并获得速度分布,然后根据质量守恒方程推导出压力修正方程,求解压力修正方程获得压力修正值,并对速度及压力进行修正。整个过程反复迭代,直到速度及压力收敛。x方向速度和压力修正值的关系式如下:
| $ \left( {{a}_{\text{e}}}-\sum{{{a}_{\text{nb}}}} \right){{{{u}'}}_{\text{e}}}={{A}_{\text{e}}}\left( {{{{P}'}}_{\text{P}}}-{{{{P}'}}_{\text{E}}} \right) $ | (12) |
式中:ae和anb为系数;u'e为表面上的速度;Ae为表面积;P'P和P'E为控制体积中心及东侧控制体中心的压力修正值,其余方向的关系式与其类似。
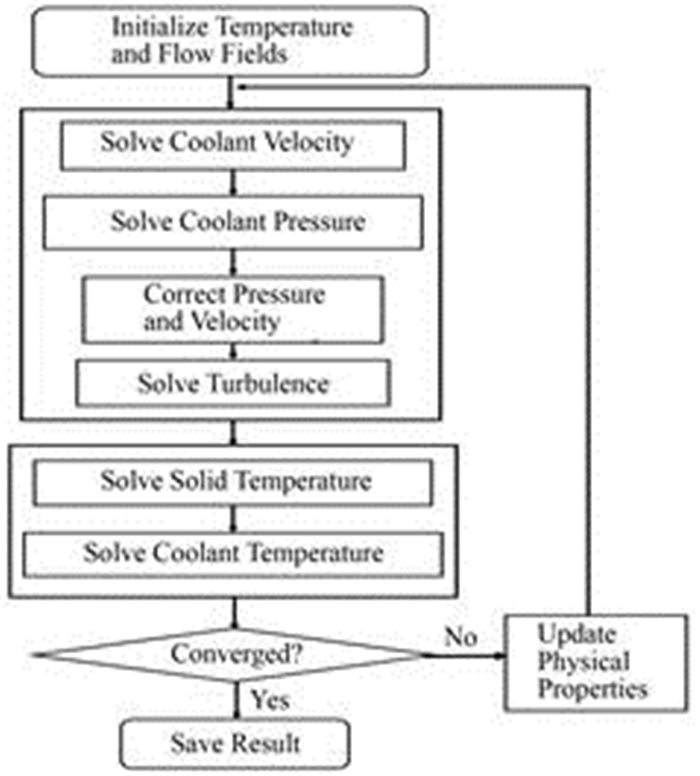
2.3 求解流程图 1显示了堆芯热工水力计算的求解流程。速度场及温度场需要不断地迭代求解,每次迭代求解后根据新的结果更新堆芯材料的热物性,直到所有物理量收敛,以上过程又称外迭代过程。而求解物理量离散产生的线性方程组过程称为内迭代过程。
|
图 1 GATH程序求解流程 Figure 1 Flowchart of solving thermal hydraulic procedure in GATH code. |
三维堆芯热工水力计算需使用大量网格,巨大的网格数量、多次的外迭代过程导致计算耗时很长,其中最耗时的部分为离散的线性方程组的内迭代过程,因此本文研究了基于GPU的迭代求解算法。
方程预处理方法能进一步加快求解过程的收敛速度。预处理算法的本质为寻找线性方程组矩阵A的近似矩阵M,M≈A,使方程组Mx=b的求解速度很快。结合预处理算法的CG[21]与BICGSTAB[22]算法描述如下:
Conjugate Gradient Method
Equation: Ax=b
Initial guess of x: x0
r0=b−Ax0, z0=M−1r0, p0=z0
for j=0, 1, …, until convergence
αj=(rj, zj)/(Apj, pj)
xj+1=xj+αjpj
rj+1=rj−αjApj
zj+1=M−1rj+1
βj=(rj+1, zj+1)/(rj, zj)
pj+1=zj+1+βjpj
end for
BICGSTAB Method
Equation: Ax=b
Initial guess of x: x0
r0=b−Ax0, p0=r0
for j=0, 1, …, until convergence
qj=M−1pj
αj=(rj, r0)/(Aqj, r0)
sj=rj−αjAqj
zj=M−1sj
ωj=(Azj, sj)/(Azj, Azj)
xj+1=xj+αjqj+ωj zj
rj+1=sj−ωjAzj
βj=(rj+1, r0)/(rj, r0)×(αj/ωj)
pj+1=rj+1+βj(pj−ωjAqj)
end for
GPU求解器的两种预处理算法为Neumann多项式算法(Neumann Polynomial Preconditioning, POLYN)[23]、几何代数多重网格法(Geometric Algebraic Multigrid Method, GAMG)。
POLYN算法根据多项式展开原理,将矩阵A−1用Neumann多项式近似表示,其计算公式如式(13),本文采用三阶多项式展开。
| $ \begin{align} & N=I-{{D}^{-1}}\boldsymbol{A} \\ & {{\boldsymbol{A}}^{-1}}\approx {{\boldsymbol{M}}^{-1}}=\left( I+N+\cdots +{{N}^{m}} \right){{D}^{-1}} \\ \end{align} $ | (13) |
本文提出了适用于规则网格的GAMG预处理算法,该算法不需要寻找矩阵A的近似矩阵。在求解方程组Ax=b时,该算法结合网格的空间信息及矩阵的代数信息,将求解过程化为由细到粗网格的迭代过程,通过在不同密度的网格进行迭代,不同频率的误差分量得到有效衰减,加快了收敛速度。
该算法以标准的光滑聚集代数多重网格法[24]为基础,利用网格的分布规律生成粗网,即空间上相邻最近的27个网格聚集为一个粗网,这种方式虽然只适用于规则网格,但相比于标准方法速度更快。
GAMG预处理法分为建立过程和求解过程。多重网格建立过程描述如下,依次为网格粗化、插值矩阵计算、方程组矩阵及右端矢量转换。其中,粗网格由插值矩阵Pk、限制矩阵PkT、粗网格层级的矩阵Mk+1和矢量bk+1组成。粗网格层级m的值一般不超过100,ω的值通常根据矩阵的谱半径计算。
GAMG setup
M0=A, b0=b
for k=0, …, m
coarsen kth hierarchy of grid and get aggregates vector: aggk
construct tentative interpolation matrix Tk based on bkand aggk
bk+1=TkTbk
Interpolation matrix Pk=(I−ωD−1Mk)Tk
Mk+1=PkTMkPk
end for
GAMG法的求解过程是一个递归过程,其算法描述如下。首先,方程组在第一层网格进行几次权重Jacobi光滑迭代,然后计算出残差r并传递到下一层较粗的网格,在下一层网格递归求解x的修正值e,进行到最后一层网格上时直接求解出结果,然后将修正值e插值到上一层网格并修正x,再进行几次权重Jacobi迭代。重复以上递归计算直到结果收敛。
GAMG Solve
GAMG_solver (Mk, Pk, xk, bk)
If k < m
xk=weight_jacobi_iter (Mk, bk)
rk=bk−Mkxk
rk+1=PkTrk
GAMG_solver (Mk+1, Pk+1, ek+1, rk+1)
ek=Pk ek+1
xk=xk+ek
xk=weight_jacobi_iter (Mk, bk)
else
solve Mkxk=bk directly
End
GAMG算法由若干矢量及矩阵线性运算组成,流程复杂,单次计算耗时长,但是在网格规模很大且物理方程难以收敛的情况下能有效加快方程的收敛速度。
3.1 GPU加速方法及程序结构采用的算法涉及了大量线性代数运算,如向量加法、向量点积、对角矩阵-向量乘法等,这些线性代数运算具有天然的并行性,使用CUDA编程语言将这些基本运算移植到GPU,从而加速求解过程。
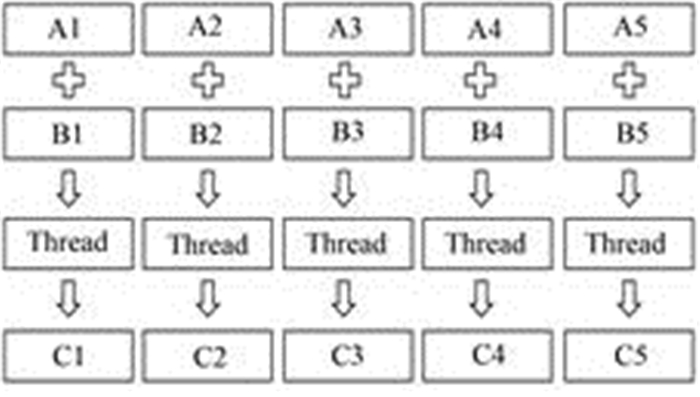
向量加减法、乘法、向量-标量运算的GPU并行计算方法相似。以向量加法为例,其并行计算过程为若干GPU的线程同时计算结果向量的某个元素,如图 2所示。
|
图 2 GPU并行计算向量加法 Figure 2 Parallel vector addition in GPU. |
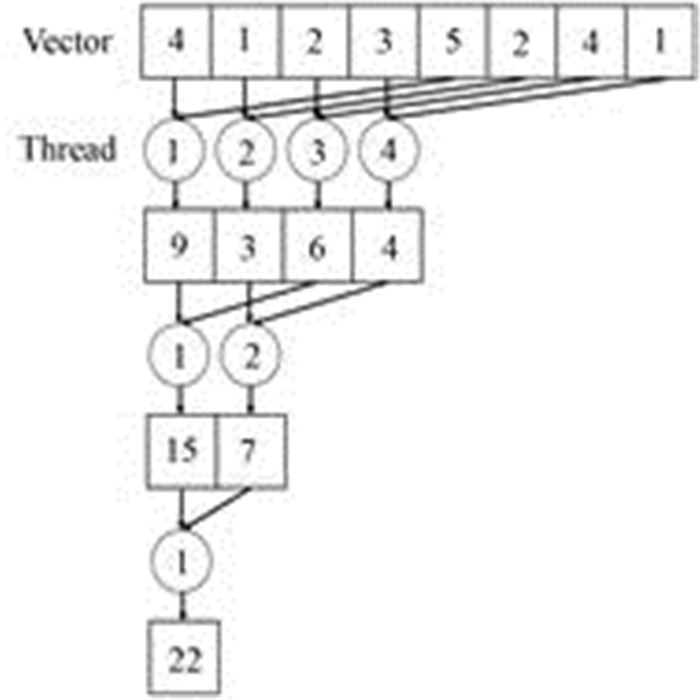
向量的点积运算由向量元素的乘法及元素间的规约求和操作完成。采用线程顺序寻址的方式进行并行规约操作,如图 3所示。对角矩阵-向量乘法算法的过程等效于每个对角线的元素与向量相乘并求和的过程。
|
图 3 GPU并行规约求和 Figure 3 Parallel summation reduction in GPU. |
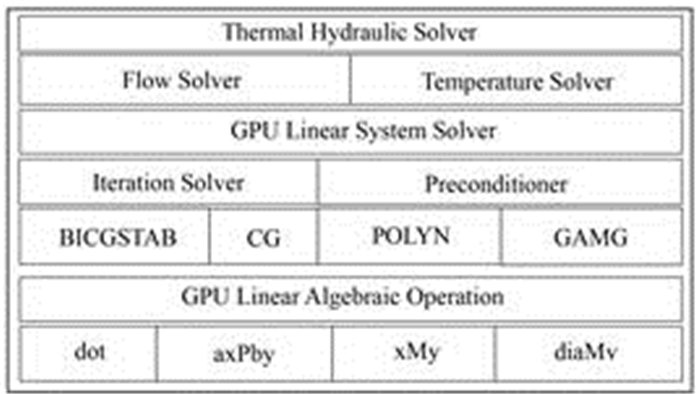
求解程序分为三个层级(图 4),底层为GPU线性代数运算模块,中间层级为基于底层模块的GPU线性方程求解模块,顶层层级为流场及温度场求解模块。两个物理求解模块执行完整的外迭代计算流程,并在对方程离散后都调用下层的GPU线性方程组求解模块进行计算。
|
图 4 GATH程序结构 Figure 4 GATH code structure. |
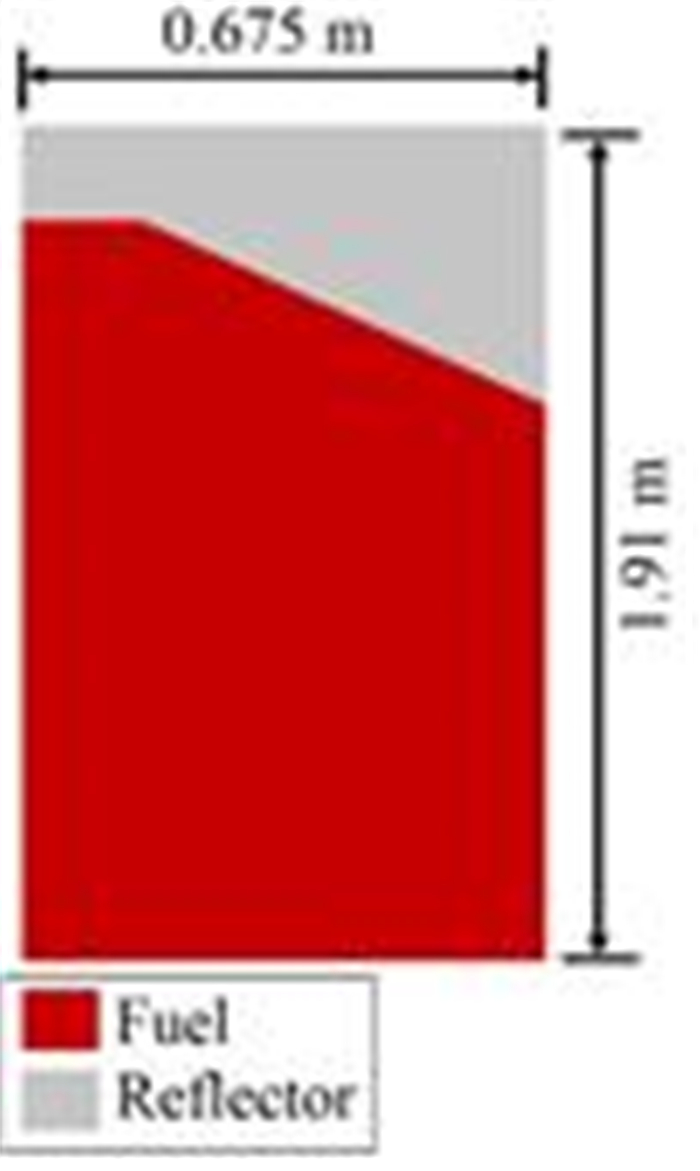
根据中国科学院上海应用物理研究所的PB-FHR实验堆设计参数建立了简化的PB-FHR堆芯几何模型,使用GATH程序对其进行热工水力分析,并与计算流体动力学(Computational Fluid Dynamics, CFD)软件的结果进行了对比。图 5为简化的堆芯模型的纵截面示意图,堆芯半径0.675 m,高1.91 m。下部区域为球床,球床区域高1.61 m,球床出口半径15 cm,球床出口处的斜面水平夹角为30°,上部区域为带若干熔盐通道的上反射层,堆芯燃料球直径为0.06 m,堆芯球床及上反射层均视为多孔介质。参考伯克利大学的实验结果[25],设PB-FHR球床孔隙为0.4,由于缺少上反射层的孔隙率测量值,假设上反射层孔隙率和球床孔隙率近似相同。
|
图 5 PB-FHR堆芯几何模型 Figure 5 Reactor core model of PB-FHR. |
堆芯内冷却剂为液态FLiBe熔盐,由于FLiBe的密度略大于燃料球的密度,燃料球在堆芯处于漂浮状态。堆芯底部为熔盐入口,入口温度873.15 K,入口流速0.052 m∙s−1,堆芯顶部为熔盐出口,出口采用流出边界条件,模型外侧壁面设为绝热。堆芯热功率为10 MW,堆芯内的功率密度分布数据由中子输运程序提供。
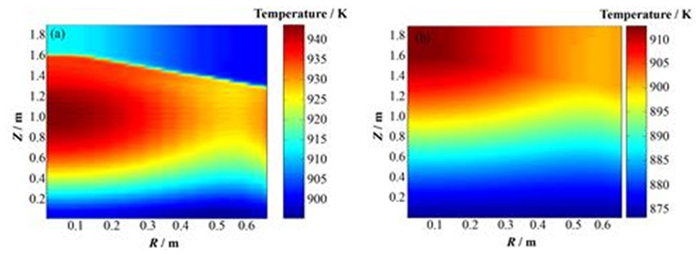
图 6(a)为GATH程序计算出的堆芯内的固相温度分布,包括球床及上反射层温度。堆芯最高温度位于中心处、高度1 m附近,堆芯入口附近区域及上反射层区域温度较低,由于外侧壁面功率有所上升,导致壁面温度也较高。图 6(b)为GATH程序计算出的堆芯冷却剂温度分布。冷却剂温度沿着堆芯纵向一直上升,并于堆芯出口达到最高。壁面附近的冷却剂也略有上升。球床多孔介质强烈的湍流热弥散效应使得冷却剂的径向温度分布比堆芯固体温度分布均匀。
|
图 6 堆芯固体(a)和冷却剂(b)温度分布 Figure 6 Temperature distribution of solid phase (a) and coolant (b) in reactor core. |
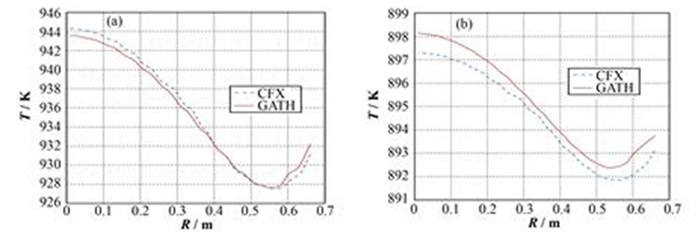
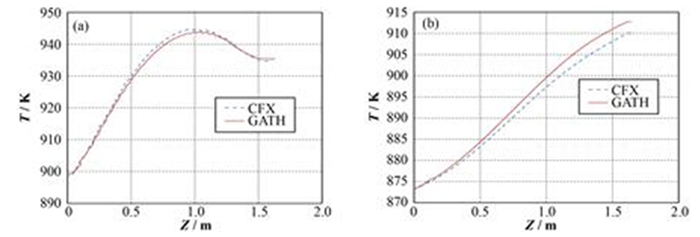
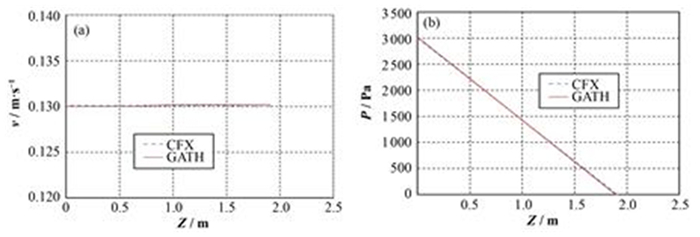
图 7−10对比了GATH程序与CFX软件的计算结果,其中堆芯径向的流场及温度分布来自堆芯中高度为1 m处的网格点。GATH计算出的流场及温度分布与CFX的结果符合得很好,所有位置的温度差异均在2 K以内。表 1显示,GATH计算结果的相对误差非常小,其中固体温度的相对误差小于冷却剂温度的误差。
|
图 7 堆芯固体(a)和冷却剂(b)径向温度分布 Figure 7 Radial temperature distribution of solid phase (a) and coolant (b) in reactor core. |
|
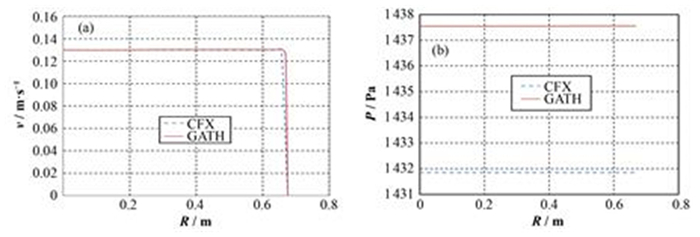
图 8 堆芯流速(a)和压力(b)径向分布 Figure 8 Radial velocity (a) and pressure (b) distribution of coolant in reactor core. |
|
图 9 堆芯固体(a)和冷却剂(b)轴向温度分布 Figure 9 Axial temperature distribution of solid phase (a) and coolant phase (b) in reactor core. |
|
图 10 堆芯流速(a)和压力(b)轴向分布 Figure 10 Axial velocity (a) and pressure (b) distribution of coolant in reactor core. |
| 表 1 GATH程序与CFX结果对比 Table 1 Comparison between GATH and CFX. |
针对每一个迭代求解算法实现了CPU串行求解器和相应的GPU并行求解器,各个版本的求解器均采用§4.1的模型进行了校核。CPU版本和GPU版本的程序均在64位Centos 6.7系统下由CUDA8.0的nvcc编译器编译。
为了分析GPU的加速性能,分别使用GPU并行求解器和CPU串行求解器进行PB-FHR堆芯热工水力计算,并统计不同求解器的耗时情况。用于测试的GPU型号为NVIDIA Tesla M2090,包含512个计算核心,运算频率1.3 MHz,双精度浮点运算速度665 Gflops(每秒6650亿次浮点运算);CPU型号为Intel Xeon X5675,运算频率3.06 GHz,单线程双精度浮点数峰值运算速度达12.24 Gflops。
将堆芯模型划分为2457600个网格,堆芯模型在径向、轴向和角度方向的划分数目分别为480、160和32。表 2显示了POLYN和GAMG预处理的迭代算法耗时情况。其中,压力修正方程和冷却剂温度方程的计算迭代次数较多,说明压力修正方程和冷却剂温度方程与其他物理方程相比不易收敛。POLYN预处理算法的加速比率最高可达20倍。GAMG预处理算法求解压力修正方程和冷却剂温度方程的计算迭代次数明显少于POLYN预处理算法,对应的求解时间也大大减少。但是GAMG预处理算法求解其他易于收敛的物理方程时比POLYN预处理算法慢。GAMG预处理算法的加速比率最高可达10倍。为了使整体求解速度最快,程序应使用GAMG预处理算法求解压力修正方程及冷却剂温度方程,而使用POLYN预处理算法求解其他物理方程。
| 表 2 POLYN预处理算法耗时 Table 2 Elapsed time of POLYN preconditioning method. |
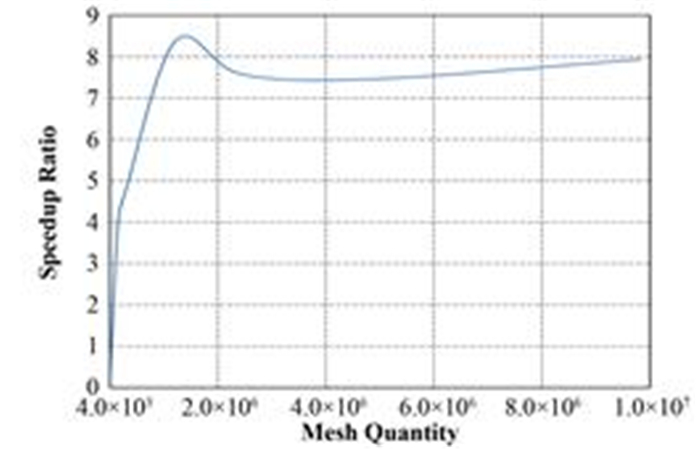
根据上文的分析,使用GAMG预处理算法求解压力修正方程及冷却剂温度方程,使用POLYN预处理算法求解其他物理方程,并统计了不同网格数量时程序整体的加速比率,统计的时间包含了方程系数的计算、数据拷贝等所有操作的耗时。结果如图 11所示,加速比率最高达8.39倍。在网格数量较小时,可并行任务较少,数据读写的时间占据较大比例,因此加速比率较低;随着网格数量的增大,可并行任务增多,加速比率开始增大;当网格数量到达一定规模后,GPU的计算资源饱和,加速比率趋于不变。
|
图 11 不同网格数量时GPU加速比率 Figure 11 Speedup ratio vs. mesh quantity. |
为进一步证明GPU加速的有效性,将GATH程序与CFX的稳态热工水力计算耗时进行了初步的对比。GATH与CFX模拟的PB-FHR堆芯模型采用相同的网格数量(449455),两个程序采用相同的收敛准则(能量残差小于10−6,其余物理量残差小于10−3),CFX采用串行计算方式,GATH采用GPU并行计算方式。GATH进行35次外迭代后结果收敛,总耗时46.25 s;CFX进行30次外迭代后结果收敛,总耗时139.88 s。因此,GPU加速比率为3.02倍。
5 结语本文基于计算流体力学方法,研发了GPU加速的PB-FHR堆芯热工水力程序,采用非热平衡多孔介质模型建立堆芯固体结构及冷却剂的物理模型,采用SIMPLEC算法求解流场及压力场,引入多孔介质的湍流模型模拟球床流体的热弥散效应,实现了可在GPU上高速运算的CG、BICGSTAB求解算法与POLYN、GAMG预处理算法。采用GATH程序对PB-FHR进行了堆芯热工水力分析,并与商用计算流体力学软件CFX的计算结果进行了对比,同时详细分析了GPU的加速性能。
结果表明:1) GATH程序与CFX的结果差异很小;2) POLYN预处理的CG及BICGSTAB算法可达20倍左右的GPU加速比率,GAMG预处理的CG及BICGSTAB算法可达10倍左右的GPU加速比率;3) 同一算法求解不同物理方程具有不同的计算效率,采用GAMG预处理算法求解压力修正方程及冷却剂温度方程而采用POLYN预处理算法求解其余物理方程可使得GATH程序整体计算速度最高;4) GATH程序整体的加速性能随着网格数量而增大,最后趋于不变,最高可达8.39倍的GPU加速比率。通过以上结果证明了GATH程序中物理模型和求解算法的正确性,并且所采用的GPU加速方法能有效提升堆芯热工水力分析的计算效率,为将来PB-FHR堆芯设计及分析提供了有效手段。
| [1] | Forsberg C W, Peterson P F, Pickard P S. Molten-salt-cooled advanced high-temperature reactor for production of hydrogen and electricity[J]. Nuclear Technology, 2003, 144(3): 289–302. DOI: 10.13182/NT03-1 |
| [2] | De Zwaan S, Boer B, Lathouwers D, et al. Static design of a liquid-salt-cooled pebble bed reactor (LSPBR)[J]. Annals of Nuclear Energy, 2007, 34(1): 83–92. DOI: 10.1016/j.anucene.2006.11.008 |
| [3] | Andreades A T C, Choi J K, Chong A Y K, et al. Technical description of the'Mark 1'pebble-bed fluoride-salt-cooled high-temperature reactor (PB-FHR) power plant[D]. Berkeley: University of California, 2014. |
| [4] | Serp J, Allibert M, Beneš O, et al. The molten salt reactor (MSR) in generation IV: overview and perspectives[J]. Progress in Nuclear Energy, 2014, 77: 308–319. DOI: 10.1016/j.pnucene.2014.02.014 |
| [5] | Griveau A. Modeling and transient analysis for the pebble bed advanced high temperature reactor (PB-AHTR)[D]. Berkeley: Department of Nuclear Engineering, University of California, 2007. |
| [6] |
牛强, 宋士雄, 魏泉, 等. 熔盐冷却球床堆热通道热工水力特性数值分析[J].
核技术, 2014, 37(7): 070602.
NIU Qiang, SONG Shixiong, WEI Quan, et al. Thermal-hydraulics numerical analyses of pebble bed advanced high temperature reactor hot channel[J]. Nuclear Techniques, 2014, 37(7): 070602. DOI: 10.11889/j.0253-3219.2014.hjs.37.070602 |
| [7] | Wang C, Xiao Y, Zhou J, et al. Computational fluid dynamics analysis of a fluoride salt-cooled pebble-bed test reactor[J]. Nuclearence & Engineering, 2014, 178(1): 86–102. DOI: 10.13182/NSE13-60 |
| [8] | Ge J, Wang C, Xiao Y, et al. Thermal-hydraulic analysis of a fluoride-salt-cooled pebble-bed reactor with CFD methodology[J]. Progress in Nuclear Energy, 2016, 91: 83–96. DOI: 10.1016/j.pnucene.2016.01.011 |
| [9] | Kirk D, Hwu W. Programming massively parallel processors[M]. Boston: Morgan Kaufmann, 2010. |
| [10] | Bailey P, Myre J, Walsh S D C, et al. Accelerating lattice boltzmann fluid flow simulations using graphics processors[C]. Proceedings of the International Conference on Parallel Processing, International Conference on Cultural Policy, Vienna, Austria, 2009: 550-557. |
| [11] | Boyd W R, Smith K, Forget B, et al. A massively parallel method of characteristic neutral particle transport code for GPUs[M]. La Grange Park, United States: American Nuclear Society, 2013. |
| [12] | De Lemos M J, Pedras M H. Recent mathematical models for turbulent flow in saturated rigid porous media[J]. Journal of Fluids Engineering, 2001, 123(4): 935–940. DOI: 10.1115/1.1413243 |
| [13] |
陶文铨.
数值传热学[M]. 西安: 西安交通大学出版社, 2003.
TAO Wenquan. Numerical heat transfer[M]. Xi'an: Xi'an Jiaotong University Press, 2003. |
| [14] | Nakayama A, Kuwahara F. A macroscopic turbulence model for flow in a porous medium[J]. Journal of Fluids Engineering, 1999, 121(2): 427–433. DOI: 10.1115/1.2822227 |
| [15] | Ergun S. Fluid flow through packed columns[J]. Chemical Engineering Progress, 1952, 48(2): 89–94. |
| [16] | Quintard M, Kaviany M, Whitaker S. Two-medium treatment of heat transfer in porous media: numerical results for effective properties[J]. Advances in Water Resources, 1997, 20(2): 77–94. DOI: 10.1016/S0309-1708(96)00024-3 |
| [17] | Kuwahara F, Nakayama A. Numerical modelling of non-Darcy convective flow in a porous medium[C]. Heat Transfer Conference, Kyongju, Korea, 1998: 411-416. |
| [18] | Wakao N, Kaguei S, Funazkri T. Effect of fluid dispersion coefficients on particle-to-fluid heat transfer coefficients in packed beds: correlation of nusselt numbers[J]. Chemical Engineering Science, 1979, 34(3): 325–336. DOI: 10.1016/0009-2509(79)85064-2 |
| [19] | Guo B, Yu A, Wright B, et al. Simulation of turbulent flow in a packed bed[J]. Chemical Engineering & Technology, 2006, 29(5): 596–603. DOI: 10.1002/ceat.200500292 |
| [20] | Kuzavkov N. Heat transport and afterheat removal for gas cooled reactors under accident conditions[D]. Vienna: International Atomic Energy Agency, 2000. |
| [21] | Hestenes M R, Stiefel E. Methods of conjugate gradients for solving linear systems[J]. Journal of Research of the National Bureau of Standards, 1952, 49(6): 409–436. DOI: 10.6028/jres.049.044 |
| [22] | Vorst H A V D. Bi-CGSTAB: a fast and smoothly converging variant of Bi-CG for the solution of nonsymmetric linear systems, SIAM J[J]. Siam Journal on Scientific & Statistical Computing, 1992, 13(2): 631–644. DOI: 10.1137/0913035 |
| [23] | Zhang J F, Zhang L. Efficient CUDA polynomial preconditioned conjugate gradient solver for finite element computation of elasticity problems[J]. Mathematical Problems in Engineering, 2013(6): 1–12. DOI: 10.1155/2013/398438 |
| [24] | Stüben K. A review of algebraic multigrid[J]. Journal of Computational & Applied Mathematics, 2001, 128(1-2): 281–309. DOI: 10.1016/S0377-0427(00)00516-1 |
| [25] | Bardet P, An J Y, Franklin J T, et al. The pebble recirculation experiment (PREX) for the AHTR[C]. Proceedings of the Advanced Nuclear Fuel Cycles and Systems (GLOBAL 2007), La Grange Park: American Nuclear Society, 2007: 845-851. |


