2. 中国科学院大学 北京 100049;
3. 上海科技大学 上海 201210
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. ShanghaiTech University, Shanghai 201210, China
熔盐作为高品质传热蓄热的工质,具有使用温度范围广、工作压力低、热转化效率高及化学性能稳定等特点,已成功应用于太阳能发电[1−2]和核能工程[3−4]等各种高温工程中。在工程系统中熔盐换热器是不可缺少的工艺设备。因此研究熔盐介质的强化换热技术对熔盐热交换器的设计和改进有指导意义。
美国橡树岭国家实验室的Hoffman和他的团队[5−6]研究了混合熔盐LiF-NaF-KF和NaNO2-KNO3-NaNO3通过具有均匀热通量的光滑管的对流传热,并给出了混合熔盐对流传热系数。Silverman等[7]通过实验手段对LiF-BeF2-ThF4-UF4和NaBF4-NaF在光滑圆管内强制对流传热进行了研究,结果表明,对于充分发展的湍流在雷诺数(Re) > 15000时,实验数据与Sieder-Tate对流传热关联式具有良好的一致性,并在实验数据和Sieder-Tate对流传热关联式的基础上获得了LiF-BeF2-ThF4-UF4和NaBF4-NaF对流换热关联式。吴玉庭等[8−10]进行了熔融盐与导热油对流传热实验,并建立了熔盐在光滑管内层流、过渡流以及湍流区域的对流传热关联式。Allman等[11]采用异型管和内插管强化熔盐的传热,并将应用到太阳能的蒸汽发生器中,以提高太阳能的热电转换效率。文玉良等[12−14]针对横纹管和螺旋槽管内的湍流和过渡流熔盐对流传热进行了研究,并建立起对流传热关联式。Chen等[15]通过实验对熔盐在具有不同结构参数的横纹管中的传热和阻力特性进行了研究,建立横纹管内对流传热和阻力的无量纲准则关联式,并对横纹管的强化传热效果进行了评估。
本文利用中国科学院钍基熔盐堆核能系统研制的三元硝酸盐KNO3-NaNO2-NaNO3(摩尔分数比为53%-40%-7%)热工实验回路(简称HTS)与导热油的对流传热实验装置,对翅片换热管湍流区的对流传热特性进行了测量,研究翅片管的强化传热并评估强化传热的效果,给出翅片管侧湍流区的对流传热计算关联式。
1 实验装置HTS熔盐热工实验回路是一个完整的预热、加热、循环、散热功能的熔盐系统,如图 1所示。系统由熔盐循环回路和油循环回路组成[16],主要包括熔盐罐、泵、加热器、实验段、导热油油箱、导热油油泵、空气冷却器、管道和气体系统等设备。HTS回路和部件都用保温层包裹以降低系统到周围环境的漏热损失。在熔盐循环回路中通过调整熔盐泵的频率改变熔盐的流量;通过设置目标温度系统自动控制调节熔盐的温度。在导热油回路中,主要通过导热油泵变化频率调节导热油的流量;通过油箱和空气冷却器调节导热油的温度。表 1列出实验中回路主要参数及调节范围。在一个工况中,首先设置目标温度调整熔盐进入套管换热器的温度;然后通过控制熔盐泵和导热油泵的频率,改变熔盐和导热油在换热管内的流速;最后通过调节油箱和空气冷却器将导热油的温度稳定在目标温度,工况稳定后,采集记录实验数据。

|
图 1 HTS熔盐实验回路图 Figure 1 Schematic diagram of HTS loop. |
| 表 1 回路主要参数 Table 1 Main parameters of the loop. |
实验对象为套管式换热器(图 2),实验段水平放置在实验装置中,其中内管为翅片管,高温HTS熔盐在内管中流动,低温导热油将在外侧流动。实验段管长L=1000 mm,翅片管基管内径di=20 mm,翅片管基管外径d=27 mm,翅片管的翅高H=15 mm,外套管的内径Z=70 mm。入口区域的长度Le=700mm,约为翅片管基管内径的25倍,其目的是在进入传热区域之前,使熔盐的流动充分发展。如图 2所示,实验中需要测量的物理量主要有熔盐进出实验段的温度为Ts, i、Ts, o;导热油进出实验段的温度为To, i、To, o;熔盐的体积流量为Vs;导热油的体积流量为Vo。翅片管以及翅片管的参数如图 3所示。

|
图 2 实验段示意图 Figure 2 Schematic diagram for heat transfer region of test section. |

|
图 3 翅片管的示意图 Figure 3 Schematic of the finned tube. |
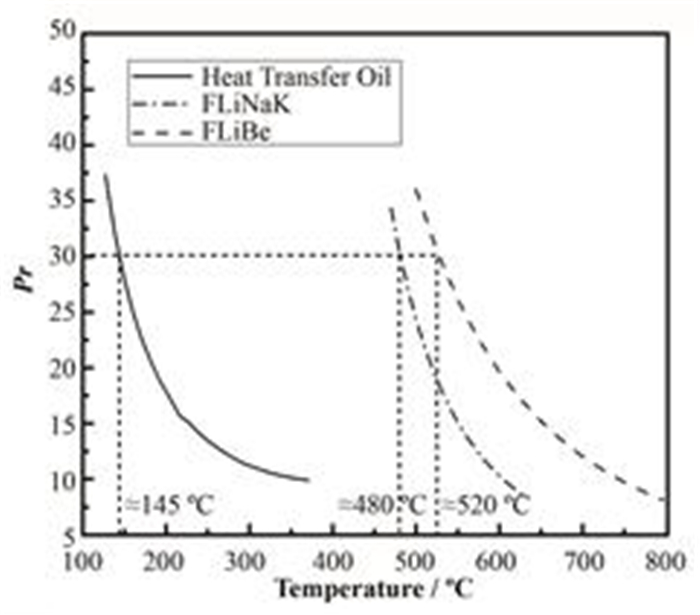
实验主要研究湍流区的对流传热特性,无论是导热油还是熔盐在翅片管中流动,都属于同类现象,并且单值性条件相似。在对流传热实验研究时,Re和普朗特数(Pr)是已定的特征数,实验中通过调节流速使导热油与熔盐在翅片管中Re相同。根据导热油物性参数、FLiNaK熔盐物性参数和FLiBe熔盐物性参数[17]计算得到导热油、FLiNaK熔盐和FLiBe熔盐的Pr与温度的关系,如图 4所示。导热油418 K的Pr (30) 与FLiNaK熔盐753 K的Pr (30) 和FLiBe熔盐793 K的Pr (30) 相同。综上所述,根据相似原理[18],使用导热油代替熔盐,开展熔盐的对流传热实验。
|
图 4 普朗特数与温度的关系 Figure 4 Pr as function of temperature. |
实验中采集数据的主要依据是热平衡原理,即管内熔融盐放出的热量与外管导热油获得的热量基本相等时采集数据。判断两侧流体换热达到热平衡的根据就是通过数据采集系统监视流体进出换热器温度,当换热管两侧流体进出口温差基本保持恒定时就可判断此时已经达到热平衡。
在实验中,通过控制HTS熔盐加热器的功率,改变HTS熔盐进入换热器的温度,HTS熔盐进入换热器温度从498 K到548 K,HTS熔盐的流速保持恒定值为(5.28±0.20) m3·h−1。实验中研究导热油湍流区的对流传热特性,导热油进入换热器的温度设定为418 K,导热油的流量由导热油泵控制,调整频率的大小改变导热油的体积流量从5.26 m3·h−1到12.96 m3·h−1。实验中熔盐和导热油的物性参数使用平均温度计算。
2.2 数据处理方法 2.2.1 基本换热过程根据实验中熔盐进出口温度、熔盐的流量、导热油进出口温度以及导热油的流量计算得到传热量:
| $ {{Q}_{\text{s}}}={{m}_{\text{s}}}{{c}_{\text{ps}}}\Delta {{T}_{\text{s}}}={{\rho }_{\text{s}}}{{V}_{\text{s}}}{{c}_{\text{ps}}}\left( {{T}_{\text{s}, \text{i}}}-{{T}_{\text{s}, \text{o}}} \right) $ | (1) |
| $ {{Q}_{\text{o}}}={{m}_{\text{o}}}{{c}_{\text{po}}}\Delta {{T}_{\text{o}}}={{\rho }_{\text{o}}}{{V}_{\text{o}}}{{c}_{\text{po}}}\left( {{T}_{\text{o}, \text{o}}}-{{Y}_{\text{o}, \text{i}}} \right) $ | (2) |
| $ {{Q}_{\text{s}}}={{Q}_{\text{loss}}}+{{Q}_{\text{o}}} $ | (3) |
| $ \begin{align} & \ {{Q}_{\text{loss}}}={{Q}_{\text{c}}}+{{Q}_{\text{r}}} \\ & \ \ \ \ \ \ \ \ ={{h}_{\text{co}}}A\left( {{T}_{\text{w}}}-{{T}_{\text{a}}} \right)+{{C}_{\text{o}}}\left[{{\left( \frac{{{T}_{\text{w}}}}{100} \right)}^{4}}+{{\left( \frac{{{T}_{\text{a}}}}{100} \right)}^{4}} \right] \\ \end{align} $ | (4) |
式中:Qs为熔盐失去的热量;Qo为导热油获得的热量;Qloss为实验损失的热量;Qc为对流损失热量;Qr为辐射损失热量;C0代表黑体辐射系数。
与熔盐失去的热量和导热油获得的热量相比,实验损失的热量很小,可忽略不计。则实验中换热量为:
| $ Q=\left( \frac{{{Q}_{\text{s}}}+{{Q}_{\text{o}}}}{2} \right) $ | (5) |
根据传热量与逆流布置的对数平均温度计算得到总传热系数K为:
| $ K=\frac{Q}{{{A}_{\text{i}}}\Delta {{T}_{\text{m}}}} $ | (6) |
式中:Q为总传热量;Ai为内表面的面积;ΔTm为对数平均温度。对数平均温度的计算公式为:
| $ \Delta {{T}_{\text{m}}}=\frac{\Delta {{T}_{\text{max}}}-\Delta {{T}_{\text{min}}}}{\ln \left( {\Delta {{T}_{\text{max}}}}/{\Delta {{T}_{\text{min}}}}\; \right)} $ | (7) |
通过翅片管式换热管的传热过程:
| $ \left\{ \begin{align} & Q={{h}_{\text{s}}}{{A}_{\text{i}}}\left( {{T}_{\text{fi}}}-{{T}_{\text{wi}}} \right) \\ & Q=\frac{\lambda }{\delta }{{A}_{\text{i}}}\left( {{T}_{\text{wi}}}+{{T}_{\text{wo}}} \right) \\ & Q={{h}_{\text{o}}}{{A}_{\text{1}}}\left( {{T}_{\text{wo}}}-{{T}_{\text{fo}}} \right)+{{h}_{\text{o}}}{{\eta }_{\text{f}}}{{A}_{2}}\left( {{T}_{\text{wo}}}-{{T}_{\text{fo}}} \right) \\ & \ \ \ ={{h}_{\text{o}}}{{\eta }_{\text{o}}}{{A}_{\text{o}}}\left( {{T}_{\text{wo}}}-{{T}_{\text{fo}}} \right) \\ \end{align} \right. $ | (8) |
式中:ηo=(A1+ηfA2)/Ao。式(9) 中消去Twi和Two:
| $ Q=\frac{{{T}_{\text{fi}}}-{{T}_{\text{fo}}}}{\frac{1}{{{h}_{\text{s}}}{{A}_{\text{i}}}}+\frac{\delta }{\lambda {{A}_{\text{i}}}}+\frac{1}{{{h}_{\text{o}}}{{\eta }_{\text{o}}}{{A}_{\text{o}}}}} $ | (9) |
总传热系数为:
| $ \frac{1}{K}=\frac{1}{{{h}_{\text{s}}}}+\frac{\delta }{\lambda }+\frac{{{A}_{\text{i}}}}{{{h}_{\text{o}}}{{\eta }_{\text{o}}}{{A}_{\text{o}}}} $ | (10) |
| $ \frac{1}{K}=\frac{1}{{{h}_{\text{s}}}}+\frac{\delta }{\lambda }+\frac{1}{{{h}_{\text{o}}}\beta {{\eta }_{\text{o}}}} $ | (11) |
式中:β=Ao/Ai,为肋化系数,即加肋后的总外表面积与内表面积之比;hs为管内熔盐侧的对流传热系数;ho为管外导热油侧的对流传热系数;λ为基管金属导热系数;δ为基管壁厚;ηf为翅片效率;ηo为翅片壁面总效率;Ao为基管外表面传热面积;A1为基管外无翅片部分传热面积;A2为基管外翅片部分表面传热面积。
实验中没有测量管壁温度,无法直接获得对流传热系数。采用威尔逊分离法[19],通过总传热系数确定换热管表面的对流传热系数。在研究导热油在翅片管外的对流传热系数时,在同一温度工况下,管内熔盐的流速不变,使得hs不变,根据威尔逊分离法,ho正比于导热油流速vo的n次幂,即:
| $ {{h}_{\text{o}}}=Cv_{\text{o}}^{n} $ | (12) |
将式(12) 代入式(11),为:
| $ \frac{1}{K}=\frac{1}{C}{{\left( \frac{1}{{{v}_{\text{o}}}} \right)}^{n}}+B $ | (13) |
式中:B、n和C为常数,通过实验数据1/K和1/vo幂函数拟合得到。因此,通过威尔逊分离法可以计算ho和Nu,并进一步评估Nu、Re和Pr之间的关系。
2.2.2 不确定性分析实验中采用PT100热电偶测量熔盐与导热油的温度,测温范围在273−673 K,测量精度为±0.5%;使用超声波流量计测量熔盐的流量,测量范围是0−10.0 m3·h−1,测量精度为±1%;使用耐高温的涡街流量计测量导热油的流量,测量范围是0−15m3·h−1,测量精度为±2%。
实验结果受各种来源误差的影响,例如测量技术、实验设施的限制、仪器的准确度和环境变化等。不确定性分析过程中忽略物性参数所带来的误差。因此基于熔盐和导热油温度的不确定性以及流量的不确定性,可以间接获得其它参数的不确定性[20]。详细的不确定性见表 2。
| 表 2 实验测量参数和不确定性 Table 2 Measured parameters and uncertainties. |
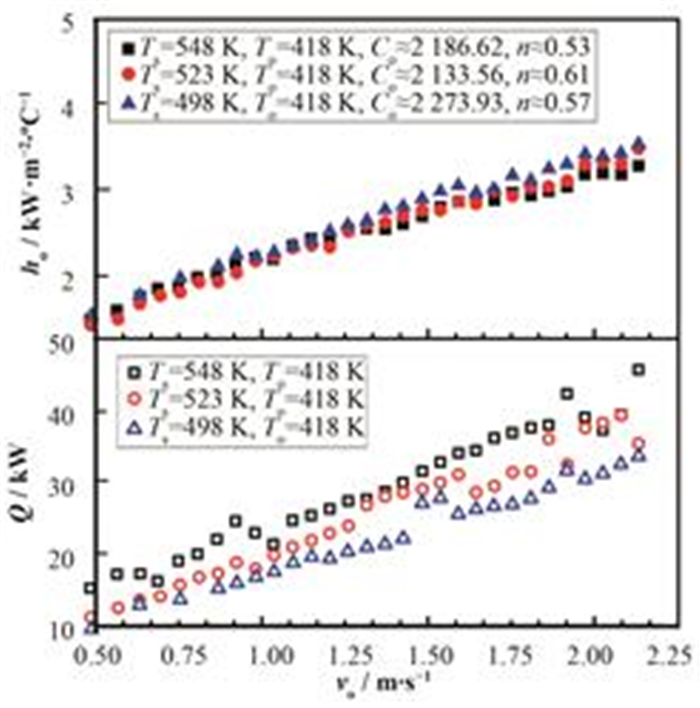
ho、Q与vo的关系如图 5所示。在相同温度下,ho和Q随着vo而增加,vo从0.48 m·s−1到2.14 m·s−1,ho从1 410.04 W·m−2·K−1增长到3534.20 W·m−2·K−1,Q从9 101.07 W增长到45 616.96 W。
|
图 5 ho、Q随vo的变化 Figure 5 Variations of ho and Q vs. vo. |
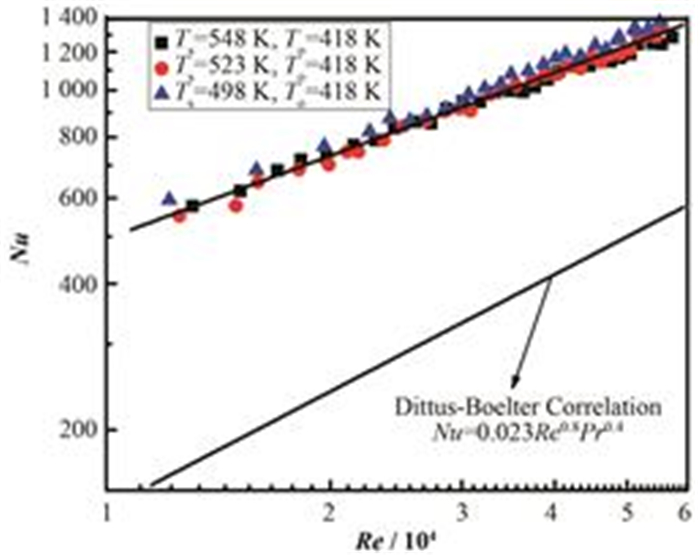
为了研究翅片管的强化传热,将导热油的Nu与Re的关系与Dittus-Boelter公式进行对比,如图 6所示。实验数据表明导热油的Nu随着Re的增加具有明显的增加,Re从12 154.45到57 535.38,Nu从550.77增加到1 380.82。实验数据与光管Dittus-Boelter公式进行对比结果表明,导热油的Nu远大于NuD-B,在Re≈30000时,实验点的Nu约为Dittus-Boelter公式的2.9倍,因此翅片管具有良好的强化换热效果。
|
图 6 在湍流区导热油的Nu-Re实验值 Figure 6 Convective heat transfer experimental data of heat transfer oil in the turbulent region. |
导热油在翅片管外侧被加热,根据传统对流传热关联式,取Pr的指数为0.4。在实验数据和传统对流传热关联式的基础上,利用最小二乘法拟合翅片管侧的湍流的对流传热关联式:
| $ \begin{align} & Nu=0.69{{{Re}}^{\text{0}\text{.57}}}{{Pr }^{0.4}} \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \left( 10\ 000\le {Re}\mathsf{<}60\ 000 \right) \\ \end{align} $ | (14) |
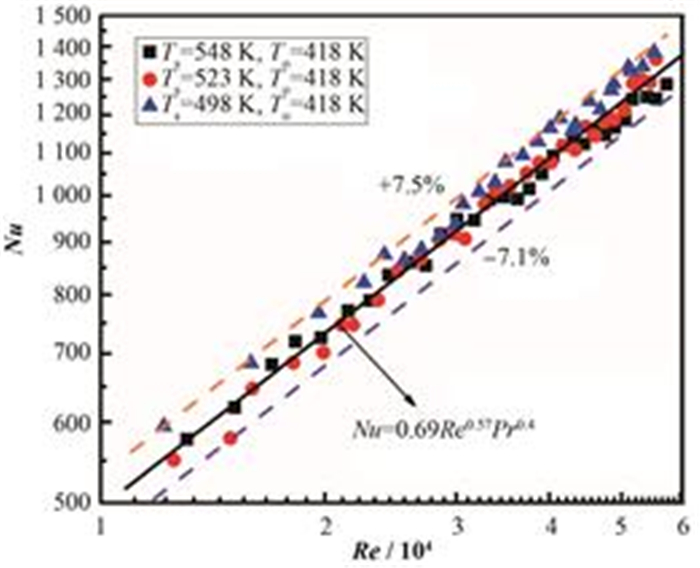
图 7为实验数据点与拟合对流传热关联式的关系图,从图 7中可以看出,拟合后对流传热关联式和实验数据点有良好的一致性,其中对流传热关联式与实验数据的相对误差分别为+7.5%与−7.1%。
|
图 7 翅片管对流传热关联式 Figure 7 Correlated correlation between Nu and Re for finned tube. |
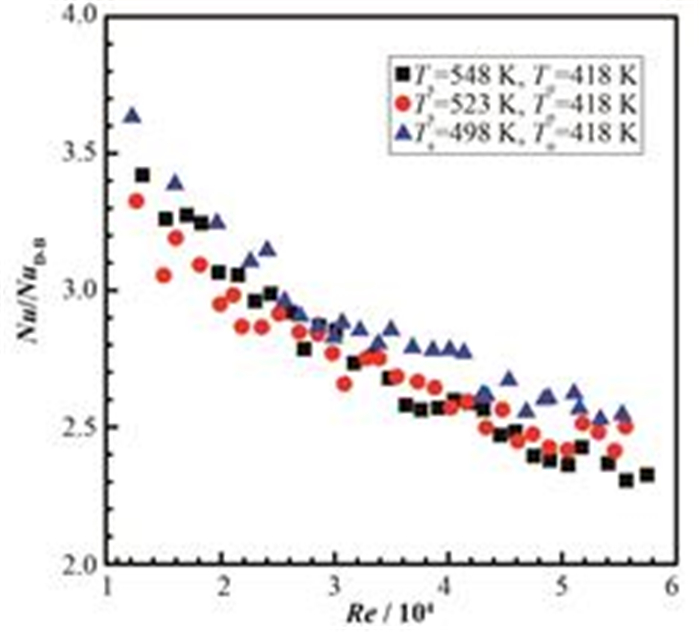
翅片管是在换热面上添加几何尺寸较大的翅片结构,其强化传热的机理分为两个方面:一是增加翅片,增加对流传热的换热面积;二是翅片的凸起破坏壁面附近的边界层。通过与传统对流传热关系式Dittus-Boelter公式对比,利用Nu/NuD-B的比值评估翅片管强化换热的效果。图 8为各实验工况下,导热油的Nu/NuD-B随Re的变化关系。从图 8可以看出,随着导热油Re从12 154.45增加到57 535.38,Nu/NuD-B的比值从3.63降低到2.32,其主要原因为翅片管的翅片效率[21]:
| $ {{\eta }_{\text{f}}}=\frac{\text{th}\left( m{H}' \right)}{m{H}'} $ | (15) |
|
图 8 翅片管强化传热 Figure 8 Evaluation of the enhanced effect in finned tube. |
式中:
| $ {H}'=H\left( 1+0.35\ln \phi \right) $ | (16) |
式中:H为翅片高度;φ=D/d,D和d分别为翅片管外径和翅片管基管外径;m的定义为:
| $ m=\sqrt{\frac{2{{h}_{\text{o}}}}{\lambda s}} $ | (17) |
式中:s是翅片厚度。根据式(15),翅片管的翅片效率随着ho增大而降低。所以实验随着Re的增大,ho增大,但翅片效率反而降低。由此可见,翅片管在低Re下的强化效果高于在高Re的强化效果。
4 结语利用HTS熔盐与导热油的对流传热实验,根据相似原理,采用导热油替代熔盐研究了流体在翅片换热管湍流区的对流传热特性,利用威尔逊分离法得到导热油在翅片管翅片侧的Nu,进一步拟合得到翅片侧湍流区的对流传热关联式。在实验数据和Dittus-Boelter对流传热关联式的基础上,采用Nu/NuD-B的方法评估强化传热,结果表明在本实验中翅片管有2.32−3.63倍的强化传热效果。
| [1] | Wu Y T, Liu S W, Xiong Y X, et al. Experimental study on the heat transfer characteristics of a low melting point salt in a parabolic trough solar collector system[J]. Applied Thermal Engineering, 2015, 89: 748–754. DOI: 10.1016/j.applthermaleng.2015.06.054 |
| [2] | Bellan S, Alam T E, Gonzalez-Aguilar J, et al. Numerical and experimental studies on heat transfer characteristics of thermal energy storage system packed with molten salt PCM capsules[J]. Applied Thermal Engineering, 2015, 90: 970–979. DOI: 10.1016/j.applthermaleng.2015.07.056 |
| [3] |
江绵恒, 徐洪杰, 戴志敏. 未来先进核裂变能——TMSR核能系统[J].
中国科学院院刊, 2012, 27(3): 366–374.
JIANG Mianheng, XU Hongjie, DAI Zhimin. Advanced fission energy program-TMSR nuclear energy system[J]. Bulletin of Chinese Academy of Sciences, 2012, 27(3): 366–374. DOI: 10.3969/j.issn.1000-3045.2012.03.016 |
| [4] | Cheng M S, Dai Z M. Development of a three dimension multi-physics code for molten salt fast reactor[J]. Nuclear Science and Techniques, 2014, 25(1): 010601. DOI: 10.13538/j.1001-8042/nst.25.010601 |
| [5] | Hoffman H W, Lones J. Fused salt heat transfer Part Ⅱ: forced convection heat transfer in circular tubes containing NaF-KF-LiF eutectic[R]. Oak Ridge: Oak Ridge National Laboratory, No. ORNL-1777, 1955. |
| [6] | Hoffman H W, Cohen S I. Fused salt heat transfer Part Ⅲ: forced convection heat transfer in circular tubes containing the salt mixture NaNO2-KNO3-NaNO3[R]. Oak Ridge: Oak Ridge National Laboratory, No. ORNL-2433, 1960. |
| [7] | Silverman M D, Huntley W R, Robertson H E. Heat transfer measurements in a forced convection loop with two molten-fluoride salts: LiF-BeF2-ThF4-UF4 and eutectic NaBF4-NaF[R]. Oak Ridge: Oak Ridge National Laboratory, No. ORNL-TM-5335, 1976. |
| [8] | Liu B, Wu Y T, Ma C F, et al. Turbulent convective heat transfer with molten salt in a circular pipe[J]. International Communications in Heat and Mass Transfer, 2009, 36: 912–916. DOI: 10.1016/j.icheatmasstransfer.2009.06.003 |
| [9] | Wu Y T, Liu B, Ma C F, et al. Convective heat transfer in the laminar-turbulent transition region with molten salt in a circular tube[J]. Experimental Thermal and Fluid Science, 2009, 33: 1128–1132. DOI: 10.1016/j.expthermflusci.2009.07.001 |
| [10] | Chen Y S, Wang Y, Zhang J H, et al. Convective heat transfer characteristics in the turbulent region of molten salt in concentric tube[J]. Applied Thermal Engineering, 2016, 98: 213–219. DOI: 10.1016/j.applthermaleng.2015.12.023 |
| [11] | Allman W A, Smith D C, Kakarala C R. The design and testing of molten salt steam generator for solar application[J]. Journal of Solar Energy Engineering, 1988, 110(1): 38–44. DOI: 10.1115/1.3268235 |
| [12] |
文玉良, 丁静, 杨晓西, 等. 高温熔盐横纹管传热特性与强化机理研究[J].
工程热物理学报, 2010, 3(1): 113–115.
WEN Yuliang, DING Jing, YANG Xiaoxi, et al. Heat transfer characteristic and enhanced mechanism of high-temperature molten salt transverse corrugated tube[J]. Journal of Engineering Thermophysics, 2010, 3(1): 113–115. |
| [13] |
沈向阳, 丁静, 陆建峰, 等. 高温熔盐在螺旋槽管内传热特性的试验研究[J].
石油机械, 2010, 38(3): 5–8.
SHEN Xiangyang, DING Jing, LU Jianfeng, et al. Heat transfer characteristic of high-temperature molten salt in spiral groove tube[J]. Petroleum Machinery, 2010, 38(3): 5–8. |
| [14] | Lu J F, Sheng X Y, Ding J, et al. Transition and turbulent convective heat transfer of molten salt in spirally grooved tube[J]. Experimental Thermal and Fluid Science, 2013, 47: 180–185. DOI: 10.1016/j.expthermflusci.2013.01.014 |
| [15] | Chen C, Wu Y T, Wang S T, et al. Experimental investigation on enhanced heat transfer in transversally corrugated tube with molten salt[J]. Experimental Thermal and Fluid Science, 2013, 47: 108–116. DOI: 10.1016/j.expthermflusci.2013.01.006 |
| [16] | Chen Y S, Zhu H H, Tian J, et al. Convective heat transfer characteristics in the laminar and transition region of molten salt in concentric tube[J]. Applied Thermal Engineering, 2017, 117: 682–688. DOI: 10.1016/j.applthermaleng.2017.01.070 |
| [17] | Williams D F, Toth L M, Clarno K T. Assessment of candidatemolten salt coolants for theadvanced high-temperature reactor(AHTR)[R]. Oak Ridge: Oak Ridge National Laboratory, 2006. |
| [18] |
戴锅生.
传热学[M]. 北京: 高等教育出版社, 1999: 114-116.
DAI Guosheng. Heat transfer[M]. Beijing: Higher Education Press, 1999: 114-116. |
| [19] | Rose J W. Heat-transfer coefficients, Wilson plots and accuracy of thermal measurements[J]. Experimental Thermal and Fluid Science, 2004, 28: 77–86. DOI: 10.1016/S0894-1777(03)00025-6 |
| [20] | Kannadasan N, Ramanathan K, Suresh S. Comparison of heat transfer and pressure drop in horizontal and vertical helically coiled heat exchanger with CuO/water based nanofluids[J]. Experimental Thermal and Fluid Science, 2012, 42: 64–70. DOI: 10.1016/j.expthermflusci.2012.03.031 |
| [21] |
刘训海, 张华. 工程计算中关于翅片效率的一个问题[J].
制冷与空调, 2008, 8(2): 25–28.
LIU Xunhai, ZHANG Hua. A problem of fin efficiency in engineering calculation[J]. Refrigeration and Air-conditioning, 2008, 8(2): 25–28. DOI: 10.3969/j.issn.1009-8402.2008.02.005 |


