2. 中国科学院大学 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
21世纪初世界各核能大国都积极地开始发展自己的熔盐堆型,使熔盐堆的研究和发展呈现出了新的气象,如:2012年美国能源部联合麻省理工学院等知名大学启动了综合研究项目,以发展熔盐冷却高温反应堆(Fluoride-salt cooled, High temperature Reactors, FHRs)的设计技术基础和商业应用[1];美国橡树岭国家实验室(Oak Ridge National Laboratory, ORNL)提出了小型模块化熔盐堆(Small Modular Advanced High-Temperature Reactor, SmAHTR)设计[2];日本各研究机构也提出了富士熔盐堆计划(Fuji Molten Salt Reactor, Fuji MSR)[3];欧盟和印度等国也在积极关注并规划各自的熔盐堆发展计划。中国科学院在2011年启动了“钍基熔盐堆核能系统”战略先导专项,以研发新一代裂变核能系统。中国科学院战略性先导专项钍基熔盐堆(Thorium-based Molten Salt Reactor, TMSR)是当今世界第四代先进反应堆的6个候选堆型之一[4-5],具有中子经济性好、放射性废物少、功率密度高和安全性能高等优点。
这类新型熔盐堆型以氟化物熔盐作为冷却剂。熔盐的成份目前主要采用热容大、中子吸收截面较小,而且在辐照环境下化学性质稳定的氟盐,如:FLiBe[6]。其特点是在常温下熔盐为固体,而在高温下(大于450 ℃)融化为液体熔盐。另外考虑到石墨材料具有良好的中子散射截面、较低的中子吸收截面、密度较大,整体表现出良好的中子慢化性能。同时在高温环境中强度高且拥有良好的导热性、低化学活性、易于机械加工等特点,是理想的反应堆中子慢化体和反射体材料。石墨在反应堆中的应用历史可以追溯到1942年世界上第一座自持的核裂变反应堆CP-1[7]。因此,在熔盐堆的设计中,核石墨作为慢化剂和结构材料应用于熔盐堆中。
石墨构件作为熔盐堆的主要组成部件,是形成承装燃料球的堆芯腔体,并构成燃料球、载热剂熔盐的流道。燃料区的燃料在堆芯中发生核反应后释放的快中子会自内向外扩散由慢化剂慢化,中子辐照剂量在石墨构件的径向会呈一定的梯度分布。在核石墨的服役过程中中子辐照的影响是研究核石墨材料特性的一个重要课题。不同大小的辐照剂量对核石墨材料特性会有不同程度的影响。另外,相比于其他堆型,熔盐堆用核石墨不仅需要忍耐高通量中子辐射和高温的持久考验,还将会与高温熔盐直接接触。液态熔盐作为冷却剂将在熔盐回路中循环流动以带出堆芯中核反应释放的热量。石墨堆芯是通过键、榫等将石墨砖限定而成。因力载荷、温度、中子辐照等的影响,石墨构件将出现应力集中区域。不同结构形态的构件,应力集中区域有所差异。在应力集中部位可能会产生新裂纹或扩展原有的裂纹。此外,核石墨构件边缘裂纹的出现将为熔盐进入核石墨内部提供通道,中子随熔盐的流入而进入核石墨内部,这将增加核石墨内部的中子辐照剂量。同时,因裂纹区域相当狭窄,高温熔盐进入后不易循环流动,极有可能在裂纹区域造成局部过热现象。
对石墨构件进行应力分析需要辐照材料性能数据库。该数据库包括辐照弹性性能、辐照蠕变性能、辐照诱导的尺寸变化和辐照条件下热膨胀系数的变化等。Tsang[8]的研究对这些性能进行了分析并指出这些性能都是快中子注量、辐照温度、氧化和熔盐渗透的函数。通常,材料的辐照性能数据是通过试验堆中的小样品材料测试获取。
为实现对辐照条件下核石墨构件的应力分析,本文利用基于球床模块堆(Pebble Bed Modular Reactor, PBMR)用核石墨材料辐照性能数据编写的一个用户自定义材料模型(User defined Material model, UMAT)[9],简化熔盐堆芯环境,借助于有限元分析商用软件ABAQUS初步研究了V型凹口对液态熔盐堆用核石墨构件应力分析的影响。该UMAT所涉及的环境温度可高达1000 ℃。
1 断裂模式根据裂纹面的相对位移断裂力学将断裂分为三种基本形式:张开型(Ⅰ型)、滑开型(Ⅱ型)和撕裂型(Ⅲ型),如图 1所示。

|
图 1 裂纹扩展的三种基本类型 (a) Ⅰ型,(b) Ⅱ型,(c) Ⅲ型 Figure 1 Three types of crack propagations. (a) Mode Ⅰ, (b) Mode Ⅱ, (c) Mode Ⅲ |
图 1(a)在上、下裂纹面沿x方向的位移分量u是相等的,沿y方向位移分量v大小相等方向相反。这类裂纹开口的上、下表面关于xz平面对称地张开。图 1(b)在上、下裂纹面沿x方向位移分量u大小相等且方向相反,而沿y方向位移分量v相等。该类裂纹开口的上、下表面关于xz平面反对称地张开。图 1(c)在上、下裂纹面沿z方向位移分量w大小相等且方向相反,而沿y方向位移分量v相等。相对于xz平面,该类裂纹开口的上、下表面关于z反对称地张开。实际石墨中的裂纹扩展是这三种基本类型的组合。在这三种类型中,第一种与高脆性材料中的裂纹扩展方式最为接近[10]。而核石墨材料属于脆性材料,为简化分析,在本文中只选取张开型裂纹模式对石墨构件进行预制裂纹处理后建立辐照模型。下文根据张开型裂纹的形态特征将其称为V型凹口裂纹。
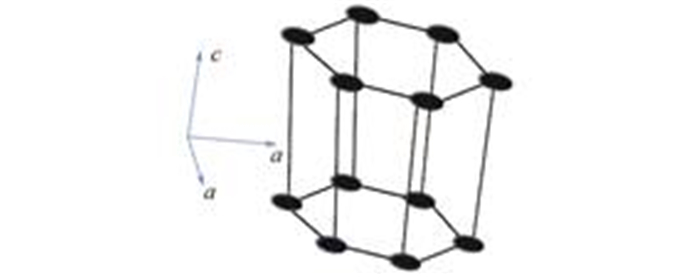
2 核石墨材料的辐照行为早期的研究[11-14]指出,石墨材料特性的改变与石墨晶体行为关系密切。理想石墨晶体由六边形层状网络结构构成,碳原子处于六边形的顶点位置。用两条主轴可以描述一个石墨晶体:平行于基平面的a轴和垂直于基平面的c轴(图 2)。辐照条件下,石墨晶体将出现c轴膨胀、a轴压缩的现象。石墨单晶通过随机聚集形成多晶颗粒,再通过特殊的制造工艺成形为石墨材料,在这个过程中石墨单晶的异向性将逐渐消失,整体表现出材料的宏观特性。Hall等[15]的研究指出温度在300-450 ℃时,随着辐照剂量的增加核石墨构件的体积会先缩小再增加(体积“回转”),出现体积“回转”之后,增加剂量构件体积会继续膨胀,当超过原始体积时,构件的物理性能会发生恶化而可能导致石墨构件失效。
|
图 2 石墨晶体示意图 Figure 2 Graphite crystal. |
ORNL的液态燃料试验熔盐堆(Molten-salt Reactor Experiment, MSRE)用核石墨构件是横截面为4.064 cm2(四周为弧形凹面)、长度为182.88cm的长条形石墨棒。为实现对TMSR石墨构件应力的初步分析,根据该尺寸为TMSR设计一款横截面为50 mm×50 mm的长条形石墨棒。石墨棒垂直置于TMSR反应堆容器中,对于熔盐完全浸没段可假设中子辐照注量分布沿该石墨构件长度方向不发生变化,而在横截面上按外围至中心位置中子辐照注量由高到低呈梯度分布,因此该类等横截面柱形体石墨构件可简化为连续实体的平面应变问题(Plane Strain, PE)。基于此,本文对石墨构件的应力进行初步分析,暂且只考虑二维情况:主要分析长条状核石墨构件横截面内不同中子辐照梯度和V型凹口裂纹的存在对石墨构件应力分布的影响。中子辐照梯度是指构件横截面外围和该横截面中心位置处的注量差与外围注量的百分比,本文选取的4个中子辐照梯度分别为:10%、15%、20%、25%。在§3.1中先不考虑构件中存在凹口的情况分析辐照梯度对构件应力分布的影响,再在§3.2中考虑有凹口的情况,分析不同凹口半宽度和辐照梯度对核石墨构件应力分析的影响。图 3为有V型凹口裂纹的二维构件有限元模型图,该模型中包括2720个8节点广义平面应变单元(Generalization plan strain element, CPEG8) 和24个6节点(CPEG6)。

|
图 3 2D石墨构件模型示意图 Figure 3 2D graphite component mode. |
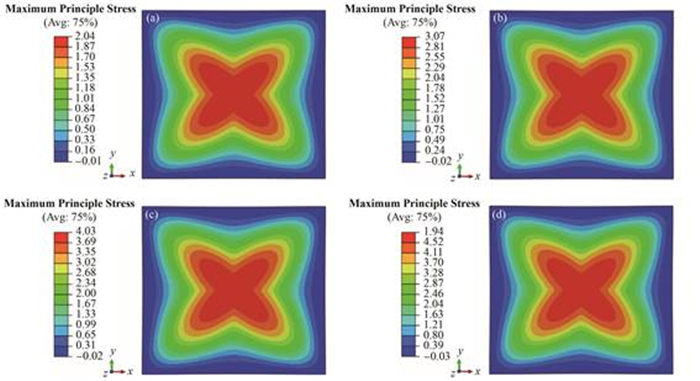
不考虑V型凹口裂纹的存在,对横截面为50mm×50 mm的正方形核石墨试件作模拟计算,探索不同中子辐照梯度对核石墨构件应力分布的影响。各试件外围中子辐照注量(最大辐照注量)均取同一值,图 4(a)-(d)试件的辐照梯度分别为10%、15%、20%、25%。各模型温度场均设为熔盐堆的堆芯环境温度650 ℃。结合新编写的UMAT建立有限元模型对该核石墨试件进行应力分析。
|
图 4 无V型凹口裂纹试件的最大主应力分布 (a)辐照梯度为10%,(b)辐照梯度为15%,(c)辐照梯度为20%,(d)辐照梯度为25% Figure 4 Maximum principle stress of non-V shape crack graphite component model. (a) The dose gradient is 10%, (b) The dose gradient is 15%, (c) The dose gradient is 20%, (d) The dose gradient is 25% |
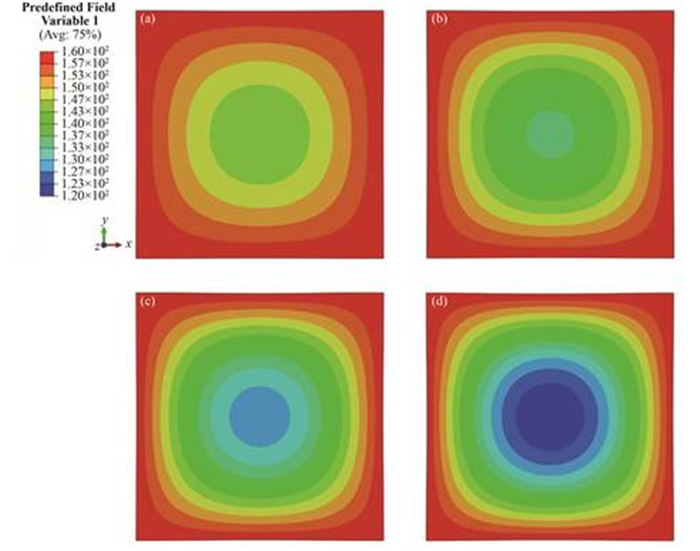
材料力学中的最大拉应力强度理论认为:无论何种状态,只要最大拉应力达到材料单向拉伸断裂时的最大拉应力值,则材料断裂。其中,某点的最大拉应力数值即最大主应力数值。因此本文中选取最大主应力作为对比标准。图 4为最大主应力分布图,表明没有预制凹口裂纹时,在辐照条件下核石墨构件最大主应力值按轴对称形式分布,构件的应力集中区域出现在构件内部中心位置及其附近区域,且辐照注量梯度越大中心区域应力集中越显著,图 4中(a)-(d)对应最大主应力值分别为:2.04 MPa、3.07 MPa、4.03 MPa、4.94 MPa。当中心区域最大主应力值超过断裂发生的临界值时,中心区域可能成为起裂点而使构件断裂失效。在模拟中将辐照注量设置为第一个预定义场变量(Predefined Field Variable 1, FV1)。图 5是各辐照梯度下构件的辐照注量分布图(单位为1020cm-2)。
|
图 5 各辐照梯度下辐照注量分布 (a)辐照梯度为10%,(b)辐照梯度为15%,(c)辐照梯度为20%,(d)辐照梯度为25% Figure 5 Dose profile of graphite component under different dose gradient. (a) The dose gradient is 10%, (b) The dose gradient is 15%, (c) The dose gradient is 20%, (d) The dose gradient is 25% |
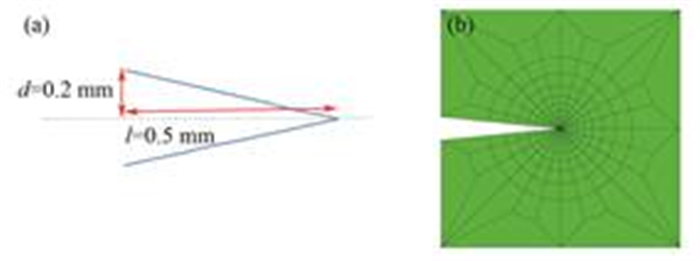
在实验中,为更好地观测裂纹扩展,通常需在试件上人为预制一个合适大小的裂纹开口。在本文的模拟中将预制裂纹开口理想化为一个V型凹口,分别选取凹口半宽度(d)为0.1 mm、0.2 mm、0.3 mm、0.4 mm、0.5 mm。V型凹口形状特征如图 6所示。Inglis[16]对均匀受力平板中的一个椭圆孔洞的应力分析表明,在一个尖锐切口或弯角处的局部应力水平可能会比外加的作用力高出许多倍,即应力集中,应力集中程度取决于孔的形状。但应力集中效应导致的应力场变化仅局限在孔的边界外极小的一个区域内,而最大的应力梯度则局限在这个小区域内的一个更小的区域中。因此对距离V型凹口裂纹尖端1 mm的区域如图 6(b)所示,进行网格细分。
|
图 6 V型凹口区域裂纹特征及网格细分 (a)裂纹特征,(b)网格细分 Figure 6 Character of V shape crack and the meshing. (a) The character of V-shape crack, (b) Refined meshing of V-shape crack |
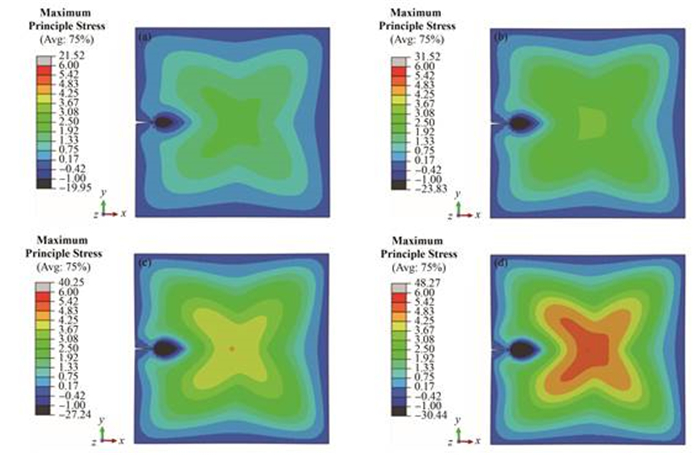
由于核石墨构件中V型凹口裂纹开口狭窄,熔盐进入该区域后循环流动受阻,可能会导致局部过热。因此在模拟中将V型凹口边界温度设为750 ℃,其他区域温度值仍为650 ℃。对同一凹口半宽度构件的最大主应力进行比较发现:1) 相比于无预制裂纹的情况,最大主应力集中区域由构件中心转移至了裂纹尖端附近区域;2) V型凹口裂纹尖端附近小区域内会出现应力集中现象,且辐照梯度越大该区域内的应力集中值越大;3) 对于同一V型凹口半宽度的构件,增大辐照梯度构件中心区域的最大主应力值增加,与无预制裂纹构件的情况相同。图 7为凹口半宽度0.5 mm构件最大主应力分布,图 7(a)-(d)构件辐照梯度分别为10%、15%、20%、25%,从图 7可见,该半宽度的凹口裂纹附近在不同辐照梯度情况下出现的应力集中区域,各辐照梯度中心位置处的最大主应力值依次为:2.30 MPa、3.42MPa、4.53 MPa、5.54 MPa。
|
图 7 V型凹口半宽度0.5 mm构件最大主应力分布 (a)辐照梯度为10%,(b)辐照梯度为15%,(c)辐照梯度为20%,(d)辐照梯度为25% Figure 7 Maximum stress of V shape crack with half width 0.5 mm. (a) The dose gradient is 10%, (b) The dose gradient is 15%, (c) The dose gradient is 20%, (d) The dose gradient is 25% |
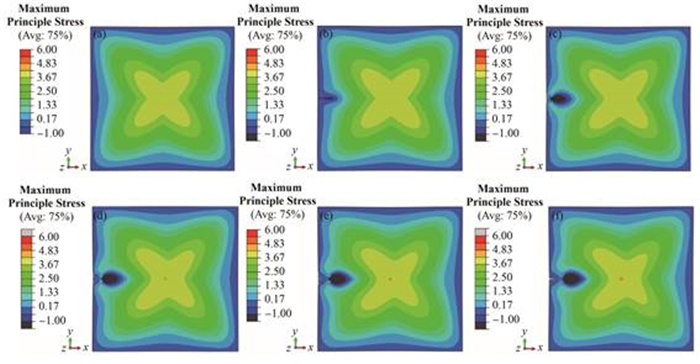
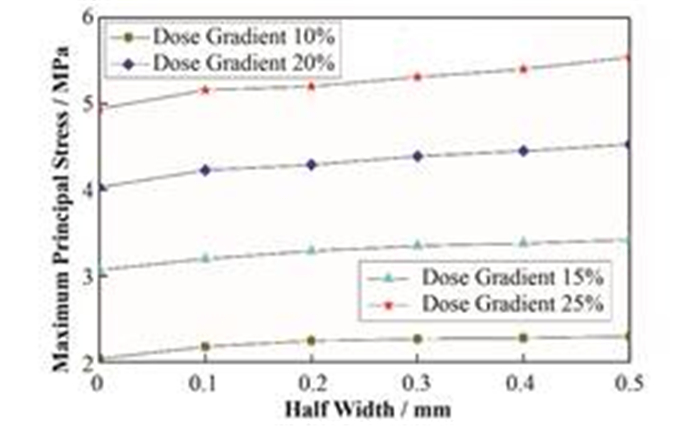
对于同一辐照梯度对比不同凹口半宽度构件的最大主应力分布情况,在不考虑裂纹扩展释放构件内部应力的情况下发现:1) 增加凹口裂纹的半宽度,会轻微增加构件中心位置处的最大主应力值。图 8是辐照梯度为20%,凹口裂纹半宽度分别为0mm、0.1 mm、0.2 mm、0.3 mm、0.4 mm、0.5 mm的构件应力分布,各构件中心位置处最大主应力值依次为:4.03 MPa、4.23 MPa、4.29 MPa、4.39 MPa、4.45 MPa、4.53 MPa。各半宽度凹口裂纹构件在不同辐照梯度条件下构件中心位置处的最大主应力值如图 9所示;2) 增加凹口裂纹的半宽度,会较大程度地增加构件裂纹尖端位置处的最大主应力值。从图 8可以看到,对于20%的辐照梯度,增大凹口裂纹半宽度,裂纹尖端附近的最大主应力值将迅速增加。对于尚未发生扩展的裂纹,处于相同条件下的构件,裂纹开口越大越容易在原有裂纹尖端处出现裂纹扩展。
|
图 8 辐照梯度为20%时不同半宽度凹口裂纹构件应力分布 (a)无凹口裂纹,(b) d=0.1 mm,(c) d=0.2 mm,(d) d=0.3 mm,(e) d=0.4 mm,(f) d=0.5 mm Figure 8 Stress of V-shape crack of different half width with dose gradient 20%. (a) Free of crack, (b) d=0.1 mm, (c) d=0.2 mm, (d) d=0.3 mm, (e) d=0.4 mm, (f) d=0.5 mm |
|
图 9 各半宽度凹口裂纹构件在不同辐照梯度下中心位置最大主应力值 Figure 9 Maximum principal stress at center point of each half width of V-shape crack under different dose gradient. |
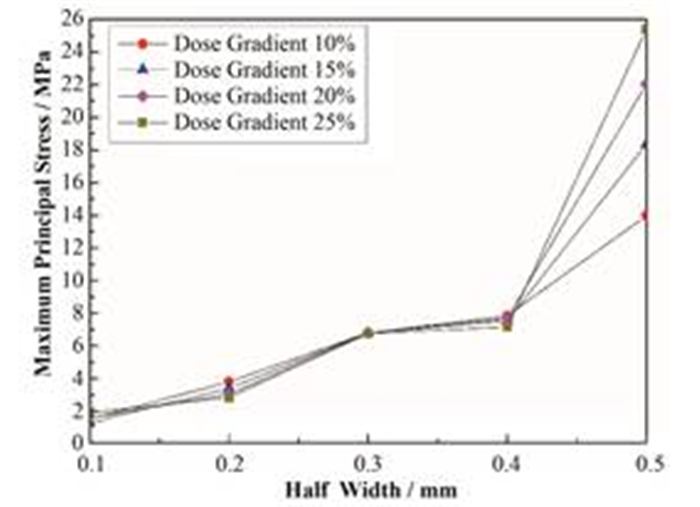
图 10为各半宽度凹口裂纹构件在不同辐照梯度条件下裂纹尖端处的最大主应力值。从图 10可以看到,同一辐照梯度下,裂纹尖端处的最大主应力值随裂纹半宽度而增加。当凹口裂纹半宽度d≤0.4mm时,裂纹尖端处的最大主应力值几乎不受辐照梯度影响;当凹口裂纹半宽度d=0.5 mm时,增大辐照梯度将增加裂纹尖端处的最大主应力值。
|
图 10 裂纹尖端处的最大主应力值 Figure 10 Maximum principal stress at crack tip. |
本文根据ORNL的MSRE用核石墨构件尺寸为TMSR设计了一款方型石墨构件,利用已编写的UMAT对核石墨构件进行了初步分析。模拟计算的结果表明,核石墨构件的应力分布受辐照梯度和预制裂纹半宽度的影响。对于无预制裂纹的构件,在辐照过程中的应力集中区域将出现在构件中心位置及其附近区域。在构件外围辐照注量相同的情况下,增大辐照梯度,构件中心区域的最大主应力值将增加,当内应力超过临界值时,构件中心位置可能成为断裂起点。对于有V型凹口预制裂纹的构件,应力集中区域将转移至预制裂纹尖端附近区域。在不考虑裂纹扩展释放内部应力的情况下,在同一辐照梯度下,增大凹口裂纹半宽度构件中心位置处的最大主应力只会略微增加,而裂纹尖端处的最大主应力值增长迅速,裂纹扩展将更可能发生在V型凹口裂纹尖端附近。对核石墨构件应力分析的相关工作将继续开展,下一步的研究分析将扩展至三维构件。
| [1] | Forsberg C W, Snead L L, Katoh Y. Fluoride-salt-cooled high-temperature reactor (FHR) with silicon-carbide-matrix coated-particle fuel[A]. Transactions of the American Nuclear Society[C]. American Nuclear Society Winter Meeting, San Diego, CA, New York: Academic Press, 2012: 907-910. |
| [2] | Greene S R, Gehin J C, Holcomb D E, et al. Pre-conceptual design of a fluoride-salt-cooled small modular advanced high temperature reactor (SmAHTR)[R]. United States: Oak Ridge National Laboratory, 2011. DOI: 10.2172/1008830. |
| [3] | Furukawa K, Erbay L B, Aykol A. A study on a symbiotic thorium breeding fuel-cycle: THORIMS-NES through FUJI[J]. Energy Conversion & Management, 2012, 63(6): 51–54. DOI: 10.1016/j.enconman.2012.01.030 |
| [4] | He Z, Gao L, Qi W. Molten FLiNaK salt infiltration into degassed nuclear graphite under inert gas pressure[J]. Carbon, 2015, 84(1): 511–518. DOI: 10.1016/j.carbon.2014.12.044 |
| [5] | Jing S, Zhang C, Pu J, et al. 3D microstructures of nuclear graphite: IG-110, NBG-18 and NG-CT-10[J]. Nuclear Science and Techniques, 2016, 27(3): 66. DOI: 10.1007/s41365-016-0071-0 |
| [6] | Haubenreich P N, Engel J R. Experience with the molten-salt reactor experiment[J]. Nuclear Applications & Technology, 1970, 8(2): 118–136. DOI: 10.13182/NT8-2-118 |
| [7] | Bodel W. The relationship between microstructure and young's modulus of nuclear graphite[D]. UK: The University of Manchester, 2013. |
| [8] | Tsang D K L, Marsden B J. Constitutive material model for the prediction of stresses in irradiated anisotropic graphite components[J]. Journal of Nuclear Materials, 2008, 381(1-2): 129–136. DOI: 10.1016/j.jnucmat.2008.07.025 |
| [9] | Tsang D K L, Marsden B J. The development of a stress analysis code for nuclear graphite components in gras-cooled reactors[J]. Journal of Nuclear Materials, 2006, 350(3): 208–220. DOI: 10.1016/j.jnucmat.2006.01.015 |
| [10] | Lawn B R. Fracture of brittle solids[M]. 2nd ed. Cambridge: Cambridge University Press, 1993. |
| [11] | Tsang D K L, Marsden B J. Effects of dimensional change strain in nuclear graphite component stress analysis[J]. Nuclear Engineering & Design, 2007, 237(9): 897–904. DOI: 10.1016/j.nucengdes.2006.01.015 |
| [12] | Tsang D K L, Marsden B J, Vreeling J A, et al. Analyses of a restrained growth graphite irradiation creep experiment[J]. Nuclear Engineering & Design, 2008, 238(11): 3026–3030. DOI: 10.1016/j.nucengdes.2007.12.017 |
| [13] | Luyken L. Using intercalation to simulate irradiation damage of nuclear graphite[D]. UK: The University of Manchester, 2012. |
| [14] | Mironov B E, Freeman H M, Brown A P, et al. Electron irradiation of nuclear graphite studied by transmission electron microscopy and electron energy loss spectroscopy[J]. Carbon, 2015, 83: 106–117. DOI: 10.1016/j.carbon.2014.11.019 |
| [15] | Hall G, Marsden B J, Smart J, et al. Finite-element modelling of nuclear-grade graphite[J]. Nuclear Energy, 2002, 41(1): 53–62. DOI: 10.1680/nuen.41.1.53.39011 |
| [16] | Inglis C E. Stress distribution in a rectangular plate having two opposing edges sheared in opposite directions[J]. Proceedings of the Royal Society of London, 1923, 103(723): 598–610. DOI: 10.1098/rspa.1923.0081 |


