2. 原子高科股份有限公司 北京 102413;
3. 同方威视技术股份有限公司 北京 100084;
4. 清华大学 工程物理系 北京 100084
2. Beijing Atom High Tech Co., Ltd., Beijing 102413, China;
3. Nuctech Company Limited, Beijing 100084, China;
4. Department of Engineering Physics, Tsinghua University, Beijing 100084, China
目前,多种类型的125I籽粒源广泛应用于永久性植入治疗肿瘤。125I籽粒源发射低能光子治疗肿瘤,具有将剂量精确地沉积在肿瘤细胞中,而不伤害肿瘤外围正常组织的优势[1-2]。
由于籽粒源治疗肿瘤主要是利用其周围剂量分布性,所以为了取得好的治疗效果,还必须知道籽粒源剂量分布情况。通过籽粒源剂量参数计算即可得到籽粒源在组织中的剂量分布,而籽粒源剂量参数可通过蒙特卡罗方法计算获得。目前,国际上采用较多的蒙特卡罗程序为MCNP5 (A General N-Particle Transport Code, Version 5)、MCNPX (Monte Carlo N-Particle eXtended)、EGSnrc (NRC’s electron gamma shower)、FLUKA (FLUktuierende KAskade)和GEANT4 (for GEometry ANd Tracking)等。以上程序均基于蒙特卡罗方法,其计算时间均较长,不能完成快速获得剂量参数结果的任务。本文将采用完全不同于蒙特卡罗方法的一种计算方法(SCALE6.1[3]中的点核积分模块QADS (Quick and Dirty Shielding))对籽粒源剂量参数计算,验证点核积分是否能够快速有效地计算籽粒源剂量参数。
1 材料和方法 1.1 SCALE6.1程序介绍SCALE为橡树岭国家实验室(Oak Ridge National Laboratory, ORNL)开发和维护的用于核安全分析和设计的综合模型和模拟套件程序包。最初,SCALE由美国核管制委员会(Nuclear Regulatory Commission, NRC)发起和开发,现在由NRC和美国能源部(Departement of Energy, DOE)支持和维护。SCALE提供全面的认证、用户友好的工具套件处理反应堆临界安全、反应堆物理、放射性屏蔽、放射源的参数描述、灵敏度和不确定度分析。本工作将使用其中的QADS模块对籽粒源进行剂量参数计算。
1.2 6711型籽粒源本工作中使用6711型籽粒源来自文献[4],由长为0.45 cm、直径为0.08 cm的圆柱体银棒作为内核,银棒表面涂 125I放射性物质,外面由钛包壳包围,籽粒源长轴两端的焊点近似为半球。具体形状如图 1所示。

|
图 1 6711型 125I籽粒源长轴方向切面 Figure 1 Longitudinal view of model 6711 125I seed source. |
使用的125I γ射线能谱数据取自文献[5],使用的材料成分来自文献[6],其中银的密度为10.5g·cm-3;钛的密度为4.54 g·cm-3;空气密度为0.001 205 g·cm-3,其中C (0.000 124)、N (0.755 268)、O (0.231 781)、Ar (0.012 827),括号内为质量份额。液态水的密度为1 g·cm-3,其中:H (0.111 898)、O (0.888 102)。
2 剂量参数和蒙特卡罗模拟 2.1 剂量参数计算公式根据AAPM TG43U1报告内容[5],可以得到籽粒源剂量和参数计算公式,其中:籽粒源参数剂量率常数Λ、径向剂量函数g(r)和各向异性函数F(r,θ)可以通过蒙特卡罗计算得到。剂量率常数Λ计算式:
| $ \mathit{\Lambda = }\frac{{\dot D\left( {{r_0}, {\theta _0}} \right)}}{{{S_K}}} $ | (1) |
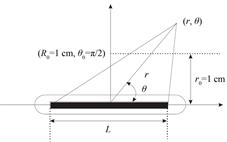
式中:SK为空气比释动能强度,cGy·h–1·cm2(用U表示);Λ为剂量率常数,cGy·h–1·U–1;D(r, θ)为某点上的剂量率;r表示离籽粒源几何中心的距离;θ表示与籽粒源长轴的夹角。D(r0, θ0)表示标准位置的剂量率,标准位置(参考点)如图 2所示。其中:r0=1;θ0=π/2;L为活性长度。
|
图 2 剂量参数计算的极坐标系统 Figure 2 Polar coordinates system used for dose parameter calculation. |
径向剂量函数g(r)和各向异性函数F(r, θ)计算:
| $ g\left( r \right) = \frac{{\dot D\left( {r, \pi /2} \right)/G\left( {r, \pi /2} \right)}}{{\dot D\left( {{r_0}, {\theta _0}} \right)/G\left( {{r_0}, {\theta _0}} \right)}} $ | (2) |
| $ F\left( {r, \theta } \right) = \frac{{\dot D\left( {r, \theta } \right)/G\left( {r, \theta } \right)}}{{\dot D\left( {r, {\theta _0}} \right)/G\left( {r, {\theta _0}} \right)}} $ | (3) |
式中:G(r, θ)为几何函数,具体意义和计算方法见文献[5]。G(r,π/2) 表示θ0=π/2时的几何函数值。
QADS能灵活设置放射源问题,不仅能模拟面源,还能模拟三维空间中任意形状和限制的放射源。大部分类型放射源能够在输入文件中直接写入代码描述。处理复杂放射源问题,还需要充分理解放射源的设置和配置。放射源描述代码包括总体归一化参数、空间网格和网格点空间分布一致性、能量结构和能谱形状一致性、放射源指定的坐标系统等。放射源几何偏离中心或者为复合源情况,使用笛卡尔(Cartesian)坐标系统。对于放射源几何偏离或复合源情况,可以描述一个整体的放射源几何,包括需要设置放射源整体,然后通过将非放射源存在区域设置为零权重,让此区域没有放射源存在。本工作将采用此种方法,先设置放射源几何为长0.3 cm、半径0.025 cm的圆柱体源,然后将圆柱体源进行网格划分,设置银棒表面权重为1,内部权重为0,达到设置圆柱体面源的效果。
2.2.2 剂量率常数Λ使用SCALE版本为SCALE6.1[3],sequence specification record:=qads。在Windows7 (32 bit)下运行。计算中源强度粒子数设置为1 s-1。单次模拟计算时间为5.94 s。空气比释动能计算将籽粒源放入半径为1.3 m的真空球体中,使用内径99cm、外径130 cm的球壳作为比释动能记录单元,内部填充材料为干燥空气。采用AIR ABS剂量计算卡记录比释动能。得到空气比释动能为3.816×10-14Gy。计算参考点(0°, 1 cm)处剂量吸收剂量,将籽粒源放入半径为1m充满液态水的球体中。得到参考点位置剂量为3.433×10-14Gy。根据式(1) 计算可得6711型 125I剂量率常数为0.900 cGy·h-1-U-1。与AAPM TG-43U1中6711型籽粒源剂量率常数推荐值0.965cGy·h-1-U-1相差6.76%。与MCNP5[7]结果0.959 cGy·h-1-U-1比较相差6.19%。可见,点核积分方法计算结果与推荐值符合较好,与蒙特卡罗方法计算结果相差不大。
2.2.3 径向剂量函数QADS计算径向剂量函数模型为将籽粒源放入半径为1 m的充满液态水的球体中。其中记录吸收剂量为点位范围为0.10-10.00 cm。采用AIR ABS剂量计算卡记录吸收剂量。得到径向剂量函数见表 1。
| 表 1 径向剂量函数 Table 1 Radial dose function g(r). |
由表 1可知,本实验与TG-43U1推荐值都符合较好(除0.1 cm、0.15 cm、0.25 cm),与TG-43U1的推荐值相比,相对偏差范围为0.02%-2.27%。与MCNP5方法计算结果比较,径向剂量函数值(不包括0.1 cm、0.15 cm、0.25 cm)最大相差6.65%,最小相差0.06%。可以看出,除了几个特别近的点外,其余点计算精度完全可以满足籽粒源剂量参数参考要求。将QADS计算结果进行5次多项式拟合,得到经验公式如下:
| $ {g_L}\left( r \right) = {a_0} + {a_1}r + {a_2}{r^2} + {a_3}{r^3} + {a_4}{r^4} + {a_5}{r^5} $ | (4) |
式中:a0=1.09936;a1=-4.45235×10-2;a2= -7.88919×10-2;a3=-1.88772×10-2;a4= -1.73590× 10-2;a5=5.79666×10-5。相关系数R=0.99992,残差平方和(Sum of Squares for Error, SSE)为2.79683×10-4,此式(4) 使用范围为r=0.5-10.0cm。显然,排除离籽粒源较近几个点外,符合很好。相关系数值很高,同时残差平方偏小。
2.2.4 各向异性函数QADS计算径向剂量函数模型为将籽粒源放入半径为1 m的充满液态水的球体中。各向异性函数计算点位为离籽粒源中心距离分别为0.5 cm、1 cm、2 cm、3 cm、4 cm、5 cm,对于相同距离角度从0°—90°分布,共66个点位。采用AIR ABS剂量计算卡记录吸收剂量。结合计算结果和式(3) 得到径向剂量函数如表 2所示。
| 表 2 各向异性函数 Table 2 Anisotropy function F(r, θ). |
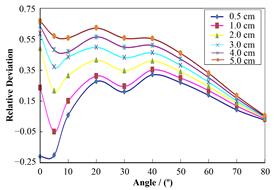
表 2即为点核积分计算各向异性函数结果,为了能获得与AAPM TG-43U1推荐值之间相对偏差更加直观的效果,将此结果与推荐值比较,做出相对偏差如图 3所示。
|
图 3 相对偏差 Figure 3 Relative deviation. |
根据图 3可以看出,点核积分计算结果与AAPM TG-43U1推荐值比较具有明显的趋势,随着距离和角度的增加,相对偏差明显减小。距离大于2 cm时,均能满足相对偏差小于30%的水平。但是由于其规律性明显,如果进行相应的修正,可以得到较理想结果。
3 结语本工作对籽粒源剂量参数理论计算进行了一次新的尝试,采用QADS的方法对籽粒源剂量参数进行计算,寻找籽粒源剂量参数计算新的方法。根据AAPM TG-43U1推荐,采用QADS计算6711型 125I籽粒源剂量参数,并将QADS计算结果与TG-43U1推荐值比较,得到剂量率常数(0.900 cGy·h-1-U-1)与AAPM TG-43U1中6711型 125I籽粒源推荐值0.965cGy·h-1-U-1相差6.76%,与MCNP5结果0.959cGy·h-1-U-1比较相差6.19%。径向剂量函数g(r)结果与TG-43U1推荐值符合很好,与TG-43U1比较,相对偏差范围为0.02%—2.27%(除0.1 cm、0.15cm、0.25 cm),与MCNP5方法计算结果比较,径向剂量函数值(不包括0.1 cm、0.15 cm、0.25 cm)最大相差6.65%,最小相差0.06%。各向异性函数F(r, θ)值与TG43U1推荐值比较,随着距离和角度的增加,相对偏差明显减小。综上所述,QADS计算6711型 125I籽粒源剂量参数结果,与AAPM TG-43U1推荐值虽然有些偏差,但是总体情况符合较好,如果对各向异性函数进行相应的修正,能得到较理想的结果。能够为籽粒源剂量参数研究提供理论计算依据,同时可以作为籽粒源应用于临床治疗的参考参数。
| [1] |
曹振, 阮锡超, 孟贝蒂, 等. MCNP5与EGSnrc比较计算125I种子源剂量参数[J].
核技术, 2014, 37(2): 020201.
CAO Zhen, RUAN Xichao, MENG Beidi, et al. Determination of dosimetric parameters for 125I seed source using MCNP5 and EGSnrc MC codes[J]. Nuclear Techniques, 2014, 37(2): 020201. DOI: 10.11889/j.0253-3219.2014.hjs.37.020201 |
| [2] | Babaheidari A E, Shamsaee M, Ahmadi P. Determination of dosimetric characteristics of a new design 125I brachytherapy source with the Monte Carlo code MCNPX[J]. Radiochemistry, 2014, 56(3): 296–301. DOI: 10.1134/S1066362214030126 |
| [3] | SCALE: a comprehensive modeling and simulation suite for nuclear safety analysis and design (Version 6.1)[R]. ORNL/TM-2005/39, Radiation Safety Information Computational Center, Oak Ridge National Laboratory, 2011. |
| [4] | Nath R, Anderson L L, Luxton G, et al. Dosimetry of interstitial brachytherapy sources: recommendations of the AAPM radiation therapy committee task group No.43[J]. Medical Physics, 1995, 22(2): 209–234. DOI: 10.1118/1.597458 |
| [5] | Rivard M J, Coursey B M, DeWerd L A, et al. Update of AAPM task group No.43 report: a revised AAPM protocol for brachytherapy dose calculations[J]. Medical Physics, 2004, 31(3): 633–674. DOI: 10.1118/1.1646040 |
| [6] | Hubbell J H, Seltzer S M. Tables of X-ray mass attenuation coefficients and mass energy-absorption coefficients 1 keV to 20 MeV for elements Z=1 to 92 and 48 additional substances of dosimetric interest[R]. Gaithersburg, MD, United States: National Institute of Standards and Technology-PL, Ionizing Radiation Division, 1995. |
| [7] |
曹振, 李飒, 张文在, 等. 6711型 125I种子源剂量参数的蒙特卡罗研究[J].
核技术, 2012, 35(5): 361–364.
CAO Zhen, LI Sa, ZHANG Wenzai, et al. M-C simulation of dosimetric characteristics of model 6711 125I seed source[J]. Nuclear Techniques, 2012, 35(5): 361–364. |


