钒自给能探测器具有结构简单、尺寸小、精度高、燃耗慢、寿命长、稳定性好、无需外部电源等特点,被广泛用作核动力反应堆的堆内固定式探测器,如CANDU (CANada Deuterium Uranium)、AP1000 (Advanced Passive pressurized water reactor)、CAP1400 (Chinese Advanced Passive pressurized water reactor)等,为堆芯功率分布测量连续不断地提供直接测量信号。堆芯功率分布测量时,利用堆芯计算软件模拟的探测器预测电流以及自给能探测器获得的测量电流,对堆芯计算软件预测的堆芯功率分布进行重构,从而获得测量的堆芯功率分布。所以,钒自给能探测器的响应电流计算方法,是基于该型探测器的堆芯功率分布测量技术的理论基础。另一方面,自给能探测器的响应机理复杂,其响应性能与材料、几何、辐照环境密切相关,并受加工制造过程的影响。在工业应用中,自给能探测器的响应性能(如中子灵敏度)一般通过堆上实验进行测量和标定,而这需要耗费大量的研发成本并增加研发的不确定性。因此,掌握探测器的响应电流计算方法,对于自给能探测器的设计优化并降低研发成本具有重要的现实意义。
自给能探测器的中子响应电流计算解析模型最早由美国巴威公司的Warren[1]提出。随后德国研究者Jaschik、Seifritz发展了自给能探测器的瞬发效应计算模型[2]。在此基础上,Warren进一步完善形成自给能探测器的响应计算模型[3]。
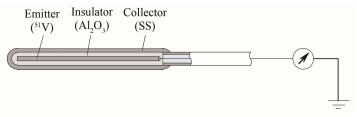
1 钒自给能探测器的响应机理与特性钒自给能探测器一般采用同轴电缆的结构形式(图 1),芯部为发射体,外部为收集极,中间填充绝缘层材料。中心的发射体是活化材料,经中子或光子辐照后,通过核反应或光原子反应释放出电子。这些电子通过绝缘层,然后被收集极收集,经同轴电缆将信号引出,直接用电流计就可测得其电流。收集到的电流与材料的β-放射性活度成正比,而材料的活度又与中子注量率成正比。所以用测量的电流值可表示探测器所在位置的中子注量率的大小。由于信号电流全来自发射体不断发射的电子,因此不需要外接电源。
|
图 1 钒自给能探测器的结构原理图 Figure 1 Schematic diagram of a vanadium self-powered detector. |
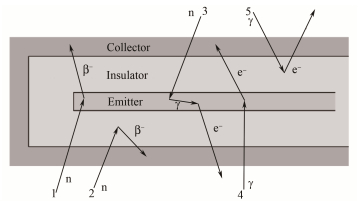
图 2给出了自给能探测器中的典型作用机理[4]。其中:1和2是中子俘获和β-衰变过程,即(n, β-)反应;3是中子俘获、释放γ射线、产生次级电子过程,即(n, γ, e-)反应;4和5是外部γ射线产生电子过程,即(γ, e-)反应。对中子响应较慢的探测器,包括钒、铑和银,过程1是主要作用机理;对中子响应较快的探测器,包括钴和铪,过程3是主要作用机理;而对伽马响应的探测器,如铂,过程4是主要作用机理。表 1给出了典型自给能探测器材料的响应特性[5]。
|
图 2 自给能探测器的典型作用机理 Figure 2 Mechanism of physical processes for a self-powered detector. |
| 表 1 典型自给能探测器材料的响应特性 Table 1 Response characteristics for typical self-powered detector material. |
钒自给能探测器的响应机理主要为51V的(n, β-)反应。51V经中子辐照后转换成放射性核素52V,进而通过β-衰变(半衰期τ1/2=224.58 s)转换成52Cr,释放出β粒子[6]。基本的核反应式如下:
| $\begin{matrix} ^{51}\text{V}+\text{n}{{\to }^{52}}\text{V}+\gamma, E\left( \gamma \right)=1.434\text{ }06\text{ MeV}, \text{ prompt} \\ ^{52}\text{V}{{\to }^{52}}\text{Cr}+{{\beta }^{-}}, E({{\beta }^{-}})=2.541\text{ }5\text{ MeV}, {{\tau }_{1/2}}=224.58\text{ s} \\ \end{matrix}$ |
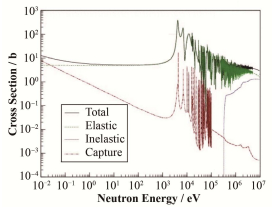
与动力堆采用的其他几种典型自给能探测器材料相比,钒探测器的响应具有以下特点:1) 51V的中子吸收截面非常小(0.0253 eV热中子吸收截面为4.9 b),对局部功率分布扰动小,燃耗速率非常低,可在非常长的使用寿命内保持高的探测精度;2) 51V的截面谱遵循1/v规律,在热中子和超热中子能区没有共振现象(图 3[6-7]),这利于探测器的中子学模拟,即采用相对简单的计算模型可获得较高的计算精度;3) 钒探测器的响应时间较长(5.5min),在使用中需进行信号延迟消除处理,以准确捕捉探测器所在位置中子注量率水平的动态变化。
|
图 3 51V的微观中子截面谱 Figure 3 Microscopic neutron cross section curves of 51V. |
根据Warren提出的理论模型,在稳态中子注量率分布中,钒探测器响应电流的基本控制方程为:
| $I=C\beta \iint{N(\vec{r})}{{\sigma }_{a}}(E)\phi (E, \vec{r})dEdV$ | (1) |
式中:I为钒探测器响应电流,A;C为电子电荷,1.602×10-19 C;β为电子逃脱概率;N为钒的核数密度,b-1∙cm-1;σa为钒的微观吸收截面,b;ϕ为探测器位置中子注量率,cm-2∙s-1;V为钒的体积,cm3。
针对商用压水堆物理计算中广泛采用的两群中子学模型,式(1) 可写成:
| $I=CV\beta N({{\sigma }_{a1}}{{\phi }_{1}}+{{\sigma }_{a2}}{{\phi }_{2}})$ | (2) |
由式(2) 可知,钒探测器响应电流的计算包括两部分:1) 探测器的吸收反应率:N(σa1ϕ1+σa2ϕ2)。其中:σa1、σa2由组件能谱计算程序获得;f1、ϕ2通过精细棒功率重构获得;N通过燃耗计算跟踪;下标1、2代表中子能群数。2) 电子逃脱概率:b。β的物理含义是探测器发射体产生的电子逃脱出发射体被收集极俘获的概率。§2.2将详细描述β的计算模型。
2.2 电子逃脱概率电子逃脱概率β的计算需考虑三个因素:电子产生、电子在发射体中的输运以及绝缘层的影响。
2.2.1 电子产生β衰变反应过程发射的β射线的能谱是连续的,发出的电子的能量具有从0到某一最大数值Eβ之间的任意数值。针对给定的β放射源,其释放出的电子的能量在E'和E'+dE'区间内的概率G(E')为:
| $G({E}')=B({E}')d{E}'$ | (3) |
其中:B(E')为归一化的β衰变能谱函数,满足:
| $\int_{0}^{{{E}_{\beta }}}{B({E}')d{E}'}=1$ | (4) |
一个能量为E'的电子输运到探测器发射体表面时剩余能量为E的概率可采用径迹长度概率函数来描述。电子在输运过程中损失能量,穿过的径迹长度为l,到达发射体表面时能量在E和E+dE之间的概率P(l)等于输运径迹长度在l和l+dl之间的概率,即:
| $P(l)=N(l)dl$ | (5) |
式中:N(l)为从发射体内到发射体表面输运径迹长度为l、单位径迹长度的概率。
径迹长度由式(6) 确定:
| $l=R({E}')-R(E)$ | (6) |
即发射体材料内能量分别为E'、E的电子射程之差。由于:
| $dl=-dR(E)$ | (7) |
| $dR(E)=-(\frac{-dE}{dx})_{E}^{-1}dE$ | (8) |
式中:(-dE/dx)E是能量为E的电子在发射体材料中的能量损失率。所以,能量为E'的电子输运到发射体表面时能量在E和E+dE之间的概率为:
| $N(l)dl=N\left[R({E}')-R(E) \right](\frac{-dE}{dx})_{E}^{-1}dE$ | (9) |
关于N(l)的详细推导可参见文献[8]。对于圆柱形发射体而言,N(l)的计算公式如下:
| $N(l)=\frac{1}{2{{r}_{e}}}+\frac{1}{2l}\begin{matrix} {} \\ \end{matrix}(p=0)$ |
| $\begin{align} &N(l)=\frac{2(1-{{p}^{2}})}{3\pi {{r}_{e}}{{p}^{2}}}K(p)-\frac{2(1-2{{p}^{2}})}{3\pi {{r}_{e}}{{p}^{2}}}E(p)-\\ &\begin{matrix} {}&{} \\ \end{matrix}{{\begin{matrix} {} \\ \end{matrix}}^{{}}}\frac{1+4{{p}^{2}}}{8\pi \alpha {{r}_{e}}{{p}^{2}}}arcsin(p)+\frac{1}{4\alpha {{r}_{e}}}+\frac{1-6{{p}^{2}}}{8\pi \alpha {{r}_{e}}p}\sqrt{1-{{p}^{2}}} \\ &\begin{matrix} {}&{} \\ \end{matrix}{{\begin{matrix} {} \\ \end{matrix}}^{{}}}\begin{matrix} {}&{}&{} \\ \end{matrix}\begin{matrix} {}&{}&{} \\ \end{matrix}\begin{matrix} {}&{}&{} \\ \end{matrix}(0 < p < 1) \\ \end{align}$ |
| $N(l)=\frac{2}{3\pi {{r}_{e}}}-\frac{1}{16\alpha {{r}_{e}}}\begin{matrix} {} \\ \end{matrix}(p=1)$ |
| $\begin{align} &N(l)=\frac{2(2{{p}^{2}}-1)}{3\pi {{r}_{e}}p}E(\frac{1}{p})-\frac{4({{p}^{2}}-1)}{3\pi {{r}_{e}}p}K(\frac{1}{p}) \\ &\begin{matrix} {}&{} \\ \end{matrix}\begin{matrix} \begin{matrix} {}&{} \\ \end{matrix}&{}&{}&{}&{} \\ \end{matrix}\begin{matrix} {}&{}&{} \\ \end{matrix}(p>1) \\ \end{align}$ | (10) |
式中:l为径迹长度,cm;re为发射体半径,cm;p=l/2re;a=L/2re,L为发射体长度,cm。
第一类完全椭圆积分:
| $\begin{align} &K(p)=\int_{0}^{\frac{\pi }{2}}{\frac{1}{\sqrt{1-{{p}^{2}}si{{n}^{2}}\theta }}d\theta } \\ &\ \ \ \ \ \text{=}\frac{\pi }{2}\cdot \left\{ 1+\sum\limits_{n=1}^{\infty }{{{\left[\frac{(2n)!}{{{2}^{n}}\cdot n!} \right]}^{2}}\cdot {{p}^{2n}}} \right\} \\ \end{align}$ |
第二类完全椭圆积分:
| $\begin{align} &E(p)=\int_{0}^{\frac{\pi }{2}}{\sqrt{1-{{p}^{2}}si{{n}^{2}}\theta }d\theta } \\ &\ \ \ \ =\frac{\pi }{2}\cdot \left\{ 1+\sum\limits_{n=1}^{\infty }{{{\left[\frac{(2n)!}{{{2}^{n}}\cdot n!} \right]}^{2}}\cdot \frac{{{p}^{2n}}}{1-2n}} \right\} \\ \end{align}$ |
径迹长度概率密度函数应用的限制条件在于体积内的径迹产生必须是均匀的,而且径迹是直线的。为了应用N(l)函数,需假设发射体区域内β衰变产生的电子是均匀的,并且沿直线输运到发射体表面。所以,发射体内的中子注量率分布应满足各向同性。尽管电子输运的径迹不总是直线的,但圆柱形发射体的对称性,可以降低大角度电子散射引入的误差。
2.2.3 绝缘层空间电荷效应由于绝缘层材料存在晶格缺陷和杂质,一些在绝缘层终止的电子将被绝缘层捕获,形成空间电荷。这样,输运到发射体表面的电子在穿过绝缘层时将受到空间电荷电场的影响。假设绝缘层的空间电荷均匀分布,体电荷密度为ρ,绝缘层材料介电常数为ε,则其电势分布V(r)满足泊松方程:
| ${{\nabla }^{2}}V(r)=-\frac{\rho }{\varepsilon }$ | (11) |
在通常工作条件下,探测器的发射极和收集极电势近似为0。在柱坐标系中,以绝缘层内外表面电势为零(V(re)=V(ri)=0)解泊松方程可得:
| $V(r)=A\left[-{{(\frac{r}{{{r}_{i}}})}^{2}}+\frac{ln(\frac{r}{{{r}_{e}}})+{{k}^{2}}ln(\frac{{{r}_{i}}}{r})}{ln(\frac{1}{k})} \right]$ | (12) |
式中:ri为绝缘层外半径,cm;r为发射体中心至绝缘层中某给定点的半径距离,cm;k=re/ri;A=
绝缘层内部的电场强度为:
| $E(r)=-\nabla V(r)=\frac{2A}{{{r}_{i}}}\left[\frac{r}{{{r}_{i}}}-\frac{1-{{k}^{2}}}{2ln(\frac{1}{k})}\cdot \frac{{{r}_{i}}}{r} \right]$ | (13) |
在绝缘层半径范围(re-ri)内,电势V(r)存在一个峰值,该处电场强度为0,电场方向发生改变,对应半径位置为:
| ${{r}_{0}}={{r}_{i}}\sqrt{\frac{1-{{k}^{2}}}{2ln(\frac{1}{k})}}$ | (14) |
在平衡状态下,如果输运到发射体表面的电子具有足够的动能,使其可以穿过绝缘层材料,到达r0位置,那么之后它将在空间电荷电场的吸引作用到达收集极,形成探测器电流;反之,如果电子在到达r0位置之前就损失了其全部动能,那么它将无法到达r0位置,在空间电荷电场力的排斥作用下,该电子将消失在发射体中。
由于发射体表面某给定点的电子可以在半球面(与该点法线夹角为[0, π/2])范围内以任意一个角度离开发射体,进入绝缘层。对电子从发射体表面至r0的径迹长度在所有角度方向进行平均,获得电子从发射体表面输运到r0位置的平均射程
| $\bar{r}={{r}_{0}}\left[E(\frac{{{r}_{e}}}{{{r}_{0}}})-\frac{{{r}_{e}}}{{{r}_{0}}} \right]$ | (15) |
式中:E(re/r0)为第二类完全椭圆积分。
依据式(15) 解得平均射程
综上,考虑能量为E'的电子产生概率、能量为E'的电子输运至发射体表面剩余能量为E的概率,对输运到发射体表面、剩余能量在Emin和Eβ之间的电子进行积分,得到最终的电子逃脱概率计算表达式如下:
| $\beta =\int_{{{E}_{min}}}^{{{E}_{\beta }}}{(\frac{-dE}{dx})_{E}^{-1}dE}\times \int_{E}^{{{E}_{\beta }}}{N\left[R({E}')-R(E) \right]B({E}')}d{E}'$ | (16) |
结合公开文献报道给出的典型钒探测器的规格与实验数据,对上述模型进行数值模拟与验证。表 2给出了典型钒探测器的设计规格参数,实验测量数据均基于热中子谱条件。
| 表 2 典型钒探测器的设计规格参数 Table 2 Design specification of typical vanadium detectors. |
为了计算电子逃脱概率以及相应的灵敏度,研究中采用FORTRAN语言编写了相应的计算模块ESCAPE。主要计算流程和重要参数如下:
1) 通过用户输入信息获取探测器吸收体材料、绝缘层材料、吸收体外径、绝缘层外径。
2) 根据式(15) 计算
3) 计算β。52V的归一化电子能谱函数采用式(17) 的形式。发射体和绝缘层材料中电子的能量损失率(-dE/dx)E和射程R(E)数据取自文献[11]。
| $B({E}')=\frac{105}{16}{{({{E}_{\beta }})}^{-\frac{7}{2}}}{{({{E}_{\beta }}-{E}')}^{2}}\sqrt{{{E}'}}$ | (17) |
4) 计算探测器电流或热中子灵敏度。计算过程中需要考虑对探测器位置绝对热中子注量率的修正。由于在实验中,探测器所在位置的绝对热中子注量率是在无探测器情况下采用活化法进行测量的,而放置探测器后将对该处中子注量率产生扰动,这种影响主要来自探测器自身的中子自屏效应以及探测器吸收引起的通量衰减效应。对于细长圆柱型的钒探测器,中子自屏效应修正因子[12]可采用式(18) 计算:
| ${{f}_{s}}=1-\frac{4}{3}N{{\sigma }_{0}}{{r}_{e}}$ | (18) |
通量衰减效应修正因子[2]采用式(19) 计算:
| ${{f}_{d}}=\frac{1}{1+\frac{3{{r}_{e}}}{2{{\lambda }_{tr}}}\left[\ln (\frac{2{{L}_{d}}}{\pi {{r}_{e}}})+\frac{3}{2}-\gamma \right]-{{f}_{s}}N{{\sigma }_{0}}{{r}_{e}}}$ | (19) |
式中:λtr为中子平均输运自由程,cm;Ld为中子扩散长度,cm;γ为欧拉常数,0.577 2。
通量衰减效应除与探测器属性(材料、尺寸)有关外,还与探测器所在位置的慢化剂属性(λtr、Ld)有关。对于轻水,λtr=0.425 cm,Ld=2.76 cm。
探测器单位长度热中子灵敏度采用式(20) 计算:
| $S=\frac{I}{\varphi L}=C\pi r_{e}^{2}\beta N{{\sigma }_{0}}{{f}_{s}}{{f}_{d}}$ | (20) |
表 3给出了钒探测器单位长度热中子灵敏度计算值与测量值的比较。从表 3可以看出,本研究的计算值与测量值相对偏差在±5%以内,与表 2中文献相当。
| 表 3 钒探测器热中子灵敏度计算值与测量值比较 Table 3 Comparison of calculated and measured thermal neutron sensitivity for vanadium detectors. |
需说明的是,本研究仅考虑了探测器发射体(n, β-)反应对探测器响应电流的贡献,未考虑热中子俘获产生的以及外部的伽马射线的贡献。根据公开的理论和实验研究报道,热中子俘获产生的以及外部的伽马射线响应对钒探测器总的电流信号贡献为5%-8%的水平[3]。
4 结语研究了钒自给能探测器的中子响应电流计算方法,采用FORTRAN语言编写了相应的计算模块ESCAPE。通过对公开报道的典型钒探测器的数值模拟分析,论证了该方法的有效性与计算精度。相关研究结果可为堆芯在线功率分布监测和钒自给能探测器的设计优化提供理论基础。
| [1] | Warren H D. Calculational model for self-powered neutron detector[J]. Nuclear Science and Engineering, 1972, 48: 331–342. |
| [2] | Jaschik W, Seifritz W. Model for calculating prompt-response self-powered neutron detectors[J]. Nuclear Science and Engineering, 1974, 53: 61–78. |
| [3] | Warren H D, Shah N H. Neutron and gamma-ray effects on self-powered in-core radiation detectors[J]. Nuclear Science and Engineering, 1974, 54: 395–415. |
| [4] | Knoll G F. Radiation detection and measurements[M]. 3rd ed. USA: John Wiley & Sons, 2000. |
| [5] | Todt W H. Characteristics of self-powered neutron detectors used in power reactors[C]. Proceedings of In-core Instrumentation and Core Assessment, Mito-shi, Japan, 1996. |
| [6] | Moreira O, Lescano H. Analysis of vanadium self powered neutron detector's signal[J]. Annals of Nuclear Energy, 2013, 58: 90–94. DOI: 10.1016/j.anucene.2013.02.027 |
| [7] | Shibata K, Iwamoto O, Nakagawa T. JENDL-4.0:a new library for nuclear science and engineering[J]. Journal of Nuclear Science and Technology, 2011, 48(1): 1–30. DOI: 10.1080/18811248.2011.9711675 |
| [8] | Snidow N L, Warren H D. Wall effect corrections in proportional counter spectrometers[J]. Nuclear Instruments and Methods, 1967, 51: 109–116. DOI: 10.1016/0029-554X(67)90369-2 |
| [9] | Andersson I Ö, Söderlund B. Vanadium beta emission detectors for reactor in-core neutron monitoring[R]. Stockholm, Sweden:Aktiebolaget Atomenergi, 1969. |
| [10] | Rao P S, Misra S C. Neutron sensitivity of vanadium self-powered neutron detectors[J]. Nuclear Instruments and Methods in Physics Research A, 1986, 253: 57–60. DOI: 10.1016/0168-9002(86)91127-7 |
| [11] | Lucien P, Evelyne B, Henri J, et al. Energy loss, range, and bremsstrahlung yield for 10-keV to 100-MeV electrons in various elements and chemical compounds[J]. Atomic Data, 1972, 4: 1–127. DOI: 10.1016/S0092-640X(72)80002-0 |
| [12] | Weinberg A M, Wigner E P. The physical theory of neutron chain reactions[C]. USA:The University of Chicago Press, 1958:711. |
