2. 中国科学院大学 北京 100049;
3. 上海科技大学 物质科学与技术学院 上海 200031
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. School of Physical Science and Technology, ShanghaiTech University, Shanghai 200031, China
人眼是一个复杂、精密的光学成像系统,外界的光信号投影到视网膜上被转换成电信号再经神经元转送到大脑重构图像。然而人眼并非完美的成像系统,存在一定程度的光学缺陷(像差)[1]。追求超高的视力一直是人类梦寐以求的目标,而减小光学像差是必经之路。早前矫正视力的办法主要通过佩戴框架眼镜或者隐形眼镜。近些年准分子激光技术的快速发展,在医学临床上的应用也越来越广泛,尤其是在眼科学的屈光治疗当中。飞秒激光技术在近视矫正中取代了角膜刀切削操作,使得手术更加快速、精确和安全,病人的体验也更加舒适。角膜屈光手术由来已久,目前市面上的手术种类也很多,例如准分子激光角膜切削术(Photorefractive Keratectomy, PRK)、准分子激光原位角膜磨镶术(Laser-assisted in situ Keratomileusis, LASIK)、全飞秒激光微小切口透镜摘除术(Small-incision Lenticule Extraction, SMILE)[2]等。随着人们对视觉质量的要求越来越高,角膜屈光手术也正向个性化发展。
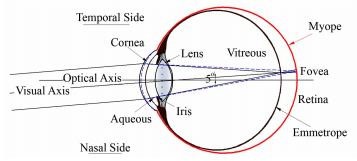
图 1是人眼示意图,沿着光线传播的方向人眼主要的结构包括:角膜、前房液、瞳孔、晶状体、玻璃体和视网膜。其中角膜和晶状体是最主要的两种屈光介质,在他们前后4个表面分别会发生折射,因此这4个表面的曲率对视觉质量的影响很大。瞳孔的孔径会随环境光线的明暗发生变化。视网膜如同光电探测器,是将光信号转换成电信号的感光组织。黄斑是视网膜上对光最敏感的部位。视轴和光轴之间有个水平方向偏鼻侧5°的Kappa角。对于正视眼而言,眼球整体的屈光度与眼球的轴长相匹配,入射的光线在经过各光学元件后聚焦在视网膜上(如图 1“Emmetrope”箭头),从而获得良好的视力。对于近视眼而言,眼球的轴长与其屈光度之间失协,玻璃体腔扩张增大,使得视网膜的位置向后移(如图 1“Myope”箭头),此时到达视网膜的离焦光斑较大造成视力模糊[3]。角膜屈光手术矫正近视的原理是通过“切削”掉相应量的角膜基质使角膜前表面变平,从而使得眼球整体的屈光度与变长了的眼轴相匹配(如图 1虚线)。
|
图 1 正视眼和近视眼的结构图以及角膜屈光手术的原理 Figure 1 Schematic diagram for emmetropic and myopic eye models, and the principle of refractive surgery. |
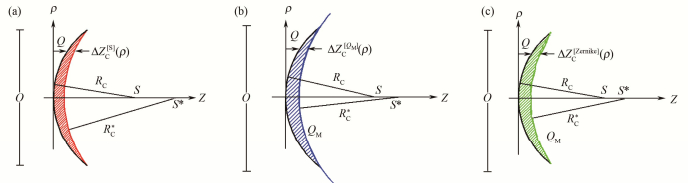
传统的LASIK手术是基于Munnerlyn公式的球面切削[4],球面修正的原理就是通过球面的“切削”角膜基质(图 2(a)),使得术后角膜前表面的曲率半径RC*变大,从而降低了角膜的屈光度。新的角膜前表面可以表示成:
| $Z_{C}^{[s]}(\rho )=\frac{{{\rho }^{2}}/R_{C}^{*}}{1+\sqrt{1-{{\rho }^{2}}/R{{_{C}^{*}}^{2}}}}$ | (1) |
| $R_{C}^{*}=\frac{({{n}_{C}}-1){{R}_{C}}}{{{S}_{E}}{{R}_{C}}+(n{}_{C}-1)}$ | (2) |
式中:nC是角膜的折射率;SE是等效球镜度(Spherical Equivalence),临床中通常使用等效球镜度来描述近视眼离焦的程度。手术中通常会先制作一个约100 μm的角膜瓣,然后再用准分子激光切削,切削的厚度(
| $\begin{align} &\Delta Z_{C}^{[s]}(\rho )=\frac{\sqrt{R_{C}^{2}-(1+Q){{\rho }^{2}}}}{1+Q}-\frac{\sqrt{R_{C}^{2}-(1+Q){{(\frac{O}{2})}^{2}}}}{1+Q}-\\ &\begin{matrix} {} \\ \end{matrix}\sqrt{R{{_{C}^{*}}^{2}}-{{\rho }^{2}}}+\sqrt{R{{_{C}^{*}}^{2}}-{{(\frac{O}{2})}^{2}}} \end{align}$ | (3) |
式中:O是瞳孔的直径(如图 2所示);Q是手术前角膜的非球面系数。手术后角膜的Q变为零。球面切削可以修正离焦和部分角膜引起的散光,但球面切削破坏了角膜原有的非球面特性,使得术后球差变大影响视力。为了保持角膜原有的特性,Q值优化的LASIK手术被提出并得到了发展[5],对于Q值优化的手术(图 2(b)),手术后角膜的前表面是扁椭球,扁椭球顶点处曲率半径为RC*,非球面系数为QM。我们模拟中QM是通过最小化波前像差优化而得。Q值优化手术后的角膜前表面为式(4),切削厚度为式(5):
| $Z_{C}^{[{{Q}_{M}}]}(\rho )=\frac{{{\rho }^{2}}/R_{C}^{*}}{1+\sqrt{1-(1+{{Q}_{M}}){{\rho }^{2}}/R{{_{C}^{*}}^{2}}}}$ | (4) |
| $\begin{align} &\Delta Z_{C}^{[{{Q}_{M}}]}(\rho )=\frac{\sqrt{R_{C}^{2}-(1+Q){{\rho }^{2}}}}{1+Q}-\frac{\sqrt{R_{C}^{2}-(1+Q){{(\frac{O}{2})}^{2}}}}{1+Q} \\ &\begin{matrix} -\\ \end{matrix}\frac{\sqrt{R{{_{C}^{*}}^{2}}-(1+{{Q}_{M}}){{\rho }^{2}}}}{1+{{Q}_{M}}}+\frac{\sqrt{R{{_{C}^{*}}^{2}}-(1+{{Q}_{M}}){{(\frac{O}{2})}^{2}}}}{1+{{Q}_{M}}} \end{align}$ | (5) |
|
图 2 三种不同屈光手术的角膜“切削”量截面(a)球面修正,(b) Q值优化,(c)波前像差引导 Figure 2 Sectional view of ablation depth in three different refractive surgeries. (a) Spherical correction, (b) Q-value optimized, (c) Wavefront guided |
事实证明Q值优化的LASIK手术术后球差得到了控制[6]。但许多患者在术后仍会抱怨在夜晚出现光晕、重影等现象[7],其原因主要是在白天光线充足的情况下,瞳孔较小,此时眼球的高阶像差可以被忽略。但在夜晚光线比较暗时,瞳孔较大,高阶像差对视力的影响会很大不容忽视。Q 值优化的LASIK手术对高阶像差的修正无能为力。近些年波前像差的理论被引入到眼科手术中[8],波前像差引导的手术也得到了快速发展,这种手术方案可以为每一位近视患者提供“量体裁衣”的服务。本次模拟中波前像差引导的手术方案就是基于Zernike面[9-10]的修正,是在基于Q值优化的基础上加上Zernike多项式的手术后角膜前表面,可以表示成:
| $Z_{C}^{[Zernike]}(\rho )=Z_{C}^{[{{Q}_{M}}]}(\rho )+\sum\limits_{n, m}{{{A}_{nm}}}Z_{n}^{m}(\rho, \theta )$ | (6) |
式中:
| $\Delta Z_{C}^{[Zernike]}(\rho )=\Delta Z_{C}^{[{{Q}_{M}}]}(\rho )+\sum\limits_{n, m}{(-{{A}_{nm}}Z_{n}^{m}(\rho, \theta ))}$ | (7) |
目前波前像差引导的技术还处于发展阶段,准确的波前测量技术、精准的三维角膜“切削”技术在理论和实验中还有很大的挑战。
1 建立模型为了建立个性化人眼模型,我们调研了许多人眼结构的研究结果和统计数据[9-11],并利用这些参数建立了通用的模型。另外近几年通过高精度的眼科测量设备可以获得角膜前后表面结构数据以及患者的波前像差,个性化的人眼模型是基于通用模型的基础上加上临床的测量数据利用光学设计软件ZEMAX建立并优化而来。对于正视眼SE=0D,本文在正视眼基础上又分别建立SE=-2D和SE=-5D(SE为等效球镜度,这里分别表示近视200度和近视500度)的近视眼模型。正视眼(0D)和近视眼(-2D和-5D)模型中主要光学元件的参数见表 1。
由表 1,角膜前表面曲率半径(RC)与近视眼术前SE成正比,RC=7.77+0.022×SE,这里SE为-2D、-5D;玻璃体腔长(LV)也与SE相关,LV =16.28-0.299×SE;晶状体被分为前后两部分:前面部分是厚度1.44mm的凸-平面,后面部分是厚度为2.16 mm的平-凹面,这两部分在555 nm光下的折射率随位置分布为:
| $\begin{align} &n_{L}^{\left( A \right)}=1.371+0.065\text{ }277\text{ }8\times z-0.022\text{ }665\text{ }9\times {{z}^{2}}-\\ &\ \ \ \ \ \ \ \ \ 00.000\text{ }203\text{ }99\times {{\rho }^{2}} \\ &n_{L}^{\left( P \right)}=1.418-0.010\text{ }073\text{ }7\times {{z}^{2}}-0.000\text{ }203\text{ }99\times {{\rho }^{2}} \\ \end{align}$ | (8) |
式中:ρ、z、θ分别为眼球的轴向、径向及旋转角度坐标。
| 表 1 正视眼(0D)和近视眼(-2D、-5D)模型的参数 Table 1 Parameters of emmetropic (0D) and myopic eye models (-2D and -5D). |
视网膜子午(X)方向和弧矢(Y)方向的曲率半径及相应的非球面系数Q为:Rr(X)=-12.91-0.094×SE,Rr(Y)=-12.72+0.004×SE,Qr(X)=0.27+0.026×SE,Qr(Y)= 0.25+0.017×SE。
为了建立一个自定义的个性化人眼模型,在晶状体后表面加了一层很薄、厚度不均匀的介质使得眼球的波前像差产生不均匀的分布。然后将眼模型的波前像差的各阶像差系数拟合到与临床测量值相同的结果。晶状体后面部分的纵向厚度(ZPL)可以横向极坐标(ρ, θ)表示为:
| ${{Z}_{PL}}\left( \rho, \theta \right)=2.16-\frac{{{\rho }^{2}}/5.9}{1+\sqrt{1-{{\rho }^{2}}/{{5.9}^{2}}}}+f(\rho, \theta )$ | (9) |
式中:f(ρ, θ)是一个任意的方程用来模拟患者个性化的眼球模型。
由于视网膜对绿光比较敏感,表 1中各光学元件的折射率值是取在555 nm。然而可见光的跨度是400-700 nm,我们的模型同样考虑到色散的效应,折射率随波长的分布为n(λ)=n(λg)+0.0512-0.1455×λ+0.0961×λ2,其中:λ代表任意的波长;λg是绿光的波长,555 nm。
波前像差通常使用Zernike多项式
| $Z_{n}^{m}(\rho, \theta )=\left\{ \begin{align} &N_{n}^{m}R_{n}^{\left| m \right|}(\rho )cos(m\theta ), \begin{matrix} {} \\ \end{matrix}m\ge 0 \\ &-N_{n}^{m}R_{n}^{\left| m \right|}(\rho )sin(\left| m \right|\theta ), \begin{matrix} {} \\ \end{matrix}m < 0 \\ \end{align} \right.$ | (10) |
其中:
| $N_{n}^{m}=\left\{ \begin{align} &\sqrt{n+1}, \begin{matrix} {} \\ \end{matrix}m=0 \\ &\sqrt{2(n+1)}, \begin{matrix} {} \\ \end{matrix}m\ne 0 \\ \end{align} \right.$ | (11) |
极半径分量
| $R_{n}^{\left| m \right|}\left( \rho \right)=\sum\limits_{s=0}^{\left( n-\left| m \right| \right)/2}{\frac{\left(-1 \right)\left( n-s \right)!}{s!\left[0.5\left( n+\left| m \right|-s \right) \right]!\left[0.5\left( n-\left| m \right|-s \right) \right]}{{\rho }^{n-2s}}}$ | (12) |
式中:阶n用来表示像差的阶次;m代表方位角频率。n=0和n=1分别是波前的平移和水平、垂直方向的倾斜,对视觉质量无影响。当n=2[m=-2, 0, 2]时多项式组代表低阶像差,主要包括离焦和像散,这些低阶像差可以通过佩戴眼镜或者隐形眼镜进行矫正。当n > 2时,代表高阶像差,主要包括球差、彗差、三叶草、四叶草像差等,这些高阶像差都是比较复杂且不对称的,佩戴眼镜、隐形眼镜或者常规的LASIK手术无法矫正。
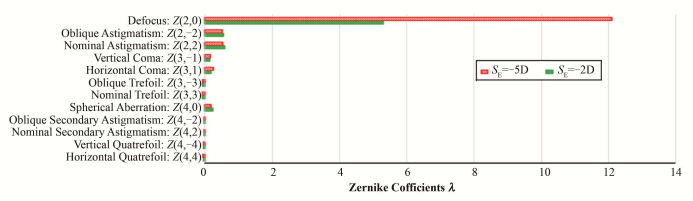
图 3中显示的条形图是-2D(纯色填充)和-5D(斜划线填充)近视眼模型术前各阶波前像差系数,以波长(555 nm)为单位。可以看出手术前的像差以离焦Z(2, 0) 为主,其次是散光Z(2, -2) 和Z(2, 2)、彗差Z(3, -1) 和Z(3, 1)、球差Z(4, 0)、三叶草像差Z(3, -3) 和Z(3, 3),其他高阶像差相对较小。其中散光不仅存在于角膜的前表面,晶状体的前后表面曲率半径或折射率的分布对散光的影响也很大。为了更加准确地反映真实的近视人眼,模型中的散光是来源于角膜和晶状体,而其他高阶像差主要是晶状体后表面的厚度分布决定的。对于-2D的模型手术前总的散光的等效柱镜度为0.42D,散光角76.2°,其中角膜的散光占总散光的92%左右。
|
图 3 -2D和-5D近视模型(6 mm)手术前波前像差系数 Figure 3 Wavefront aberration cofficients for -2D and -5D model (6 mm) before surgery. |
在对真实人眼的光学特性以及屈光手术的原理有了系统的研究后,我们利用个性化的模型对传统的球面“切削”、Q值优化以及波前像差引导的手术进行研究、分析和对比。利用光线追迹软件ZEMAX和自主研发的一些脚本文件来分析手术前后视网膜上的光斑分布及点扩散函数(Point Spread Function, PSF)。将PSF做归一化的空间傅里叶变换取模后得到调制传递函数(Modulation Transfer Function, MTF)来反映视网膜黄斑上的光学空间分辨率[12]。最后利用波前像差图(单色光555 nm)来直观的反映不同手术前后视觉质量的变化。因为有许多关于术后夜视力下降的报道,在白天的视力都很正常,所以本次模拟主要评估手术前后大瞳孔直径(6 mm)下的视觉质量。
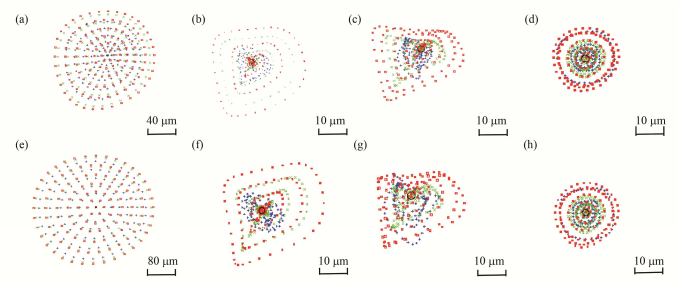
2 结果与分析图 4显示了手术前后视网膜黄斑处的光斑。模拟中选择的入射波段横跨可见光区域(红光700nm,绿光555 nm,蓝光400 nm)。对于-2D瞳孔6 mm的近视的模型,手术前均方根(Root Mean Square, RMS)半径约78.2 μm,而典型的视网膜细胞的大小只有2-4μm[13],因此会造成视力的严重模糊。在接受球面“切削”或Q值优化的矫正后,RMS半径分别显著下降到19.3 μm和11.5 μm,这两种方案对于离焦都基本上得到了修正。波前像差引导的(Zernike面)[14-15]修正术后光斑RMS半径最小约9.5mm(瞳孔大小6 mm),并且Zernike修正后在明视场(瞳孔大小3 mm)时RMS半径达到5 μm,非常接近视网膜的分辨率。从对称性也可以很明显看出Zernike修正后的光斑更好,球面修正和Q值优化修正只矫正了部分角膜散光,眼内散光及其他高阶像差并没有消除(散光和这些高阶像差是非对称的),所以对称性很差。球面修正和Q值修正后的光斑图轮廓很相似,但Q值优化的RMS半径值会更小一点,主要是因为Q值优化减小了术后球差的增加。
|
图 4 -2D和-5D近视模型手术前后视网膜光斑分布 (a)-2D模型手术前,(b)-2D模型球面修正,(c)-2D模型Q值优化修正,(d) -2D模型波前像差引导修正,(e) -5D模型手术前,(f) -5D模型球面修正,(g) -5D模型Q值优化修正,(h) -5D模型波前像差引导修正 Figure 4 Spot diagram at fovea zone on the retina for the myopic eye model of -2D and -5D before and after surgery. (a)-2D model before surgery, (b)-2D model spherical correction, (c)-2D model optimized-Q correction, (d) -2D model wavefront guided, (e) -5D model before surgery, (f) -5D model spherical correction, (g) -5D model optimized-Q correction, (h) -5D model wavefront guided |
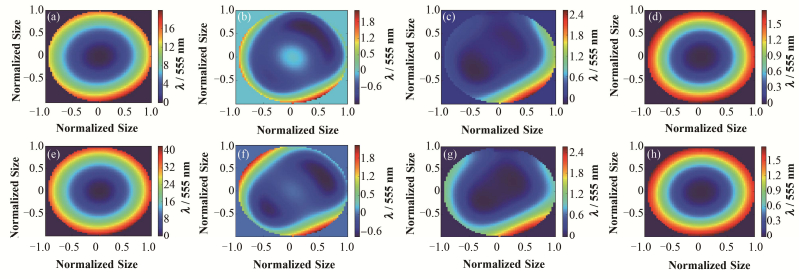
图 5展示了-2D和-5D近视眼模型手术前后整个眼球的波前像差。图 5(a)、(e)分别是-2D和-5D近视手术前的波前像差,因为手术前的像差中以离焦为主(见图 3),其数值上远高于其它的波前像差因子,并且离焦是对称的,所以手术前的波前像差的对称性相对较好。-2D的模型由于近视度数不是很高,散光对其的影响相对会比较明显,因而它的对称性相比-5D模型会差一些。图 5(b)、(c)、(f)、(g)分别是球面“切削”和Q值优化修正的波前像差图,首先从数字上可以看出,两者对离焦都有很好的修正,但对称性都不是很理想,特别是这4张图都呈现了特定角度的马鞍形分布,说明这两种矫正方案对眼内的散光没有修正。对于球面修正波前像差中出现了负值,主要是由于球面修正引入了很大的正球差。图 5(d)、(h)是采用波前像差引导的手术方案(Zernike修正),无论从数值还是对称性上,波前像差引导的技术都比其他手术方案显示很大的优越性。不仅修正了离焦和角膜散光,对眼内的散光和其他高阶像差都能有很好的修正。目前对于眼内的大散光问题,角膜屈光手术还不能解决,只能通过晶状体手术矫正,而波前像差引导的手术可以根据每个人特有的视力特征提供个性化的角膜“切削”,从而达到超高视力的要求。
|
图 5 -2D和-5D模型手术前后波前像差的比较 (a)-2D模型手术前,(b)-2D模型球面修正,(c)-2D模型Q值优化修正,(d) -2D模型波前像差引导修正,(e) -5D模型手术前,(f) -5D模型球面修正,(g) -5D模型Q值优化修正,(h) -5D模型波前像差引导修正 Figure 5 Simulated wave-front aberration distribution maps of -2D and -5D before and after the laser surgery. (a)-2D model before surgery, (b)-2D model spherical correction, (c)-2D model optimized-Q correction, (d) -2D model wavefront guided, (e) -5D model before surgery, (f) -5D model spherical correction, (g) -5D model optimized-Q correction, (h) -5D model wavefront guided |
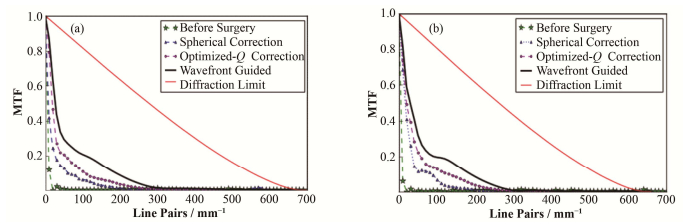
图 6是-2D和-5D模型手术前后的MTF函数曲线。细实线代表着没有像差的衍射极限,对于6mm的瞳孔其截止频率为每毫米700线对(可反映其空间分辨能力)。图 6中带星号的虚线是手术前的MTF,手术前的MTF随着空间频率的增长迅速下降,也就意味着手术前的视觉质量很差。三角形、圆形虚线和加粗实线分别代表球面修正、Q值优化修正和波前像差修正的MTF曲线,与手术之前的相比有了很明显的改善。同样的Zernike修正后(粗实线)获得最好的MTF值。MTF曲线是与人眼像差相关的(像差越小MTF值越高),所以Zernike修正比其他手术方案带来了更好的术后视力。
|
图 6 -2D (a)和-5D (b)模型手术前后MTF曲线的对比 Figure 6 MTF curves of -2D (a) and -5D (b) models before and after surgery. |
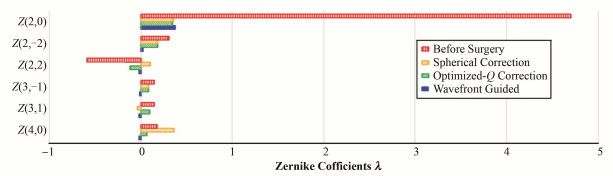
图 7展示了-2D模型手术前后低阶和部分主要高阶像差系数的变化。Z(2, 0) 是离焦项,手术前(斜线填充)离焦量约4.7λ (555 nm),三种手术方案对离焦的修正都可以减小到0.3λ左右。也就是每种手术都可以很好地矫正近视。Z(2, 2) 和Z(2, -2) 分别是倾斜和垂直方向上的散光,球面修正(点线填充)和Q值优化修正(竖线填充)相比手术前(纯色填充)的散光都有所减小,但并没有完全修正。主要是因为角膜上的散光矫正了,而晶状体内的散光没有修正,而Zernike修正了所有的散光项。Z(3, -1) 和Z(3, 1) 分别是水平和垂直方向的彗差,三种手术方案较手术前都有所减小,其中以Zernike修正尤为突出。最后一项Z(4, 0) 是球差项,明显看出球面修正(点线)后的球差比手术前增长了两倍多(从0.17λ→0.36l),Q值优化修正(斜线填充)对球差的抑制有很明显的作用,Zernike修正后的球差仍然是最好的。总的来说,波前像差引导的手术术后离焦与其他手术相近,但在散光和其他高阶像差上相比的优势非常明显,可以解决当前主流LASIK手术后造成夜视力下降的问题。
|
图 7 -2D模型(6 mm)不同手术前后各阶像差的变化 Figure 7 Absolute values of various orders of the optical aberrations for the -2D model (6 mm) before and after surgery. |
为了理解和解决近期频繁的报道在成功接受传统角膜屈光手术后,患者仍有夜视力下降的问题,我们系统地研究了人眼的光学特性和屈光手术的原理。在基于Atchison和其他研究工作者的研究成果基础上[9-10],分别建立了-2D和-5D的个性化近视眼模型,并利用三种不同的角膜手术方案(球面、Q值优化、Zernike修正)对其进行修正。然后用三种不同的评价方法对不同手术方案手术前后成像质量进行了比较。我们发现球面修正可以矫正基本的近视(即离焦像差)问题,但会引入很高的球差。Q值优化可以减小球差,但对眼内散光及其他高阶像差没有作用。这也正是传统的角膜手术后,白天视力正常而夜晚瞳孔较大时,高阶像差没有消除带来的夜视力下降问题的根源。波前像差引导的方案不仅可以修正离焦、散光等低阶像差,对高阶像差也有很好的抑制作用,使得矫正后即使在夜晚大瞳孔情况下的整个眼球的波前像差也很小,因此夜视力得到了了很大的改善。
值得提出来的是,我们的眼模型是普遍适用的,可以根据临床或实验测得的数据再现真实人眼的模型,对手术方案的选择,以及术后视觉质量客观的评判有着很大的帮助。最后需要指出的是,波前像差引导的手术对术前精确的波前测量、眼球追踪、中心定位技术、激光“切削”技术的要求都非常高,很多问题有待我们更深入地研究和探索。
| [1] | Millodot M. Dictionary of optometry and visual science[M]. Elsevier Health Sciences, 2014. |
| [2] | Reinstein D Z, Archer T J, Gobbe M. The history of LASIK[J]. Journal of Refractive Surgery, 2012, 28(4): 291–298. DOI: 10.3928/1081597X-20120229-01 |
| [3] | Scott R, Grosvenor T. Structural model for emmetropic and myopic eyes[J]. Ophthalmic & Physiological Optics, 1993, 13(1): 41–47. |
| [4] | Munnerlyn C R, Koons S J, Marshall J. Photorefractive keratectomy:a technique for laser refractive surgery[J]. Journal of Cataract & Refractive Surgery, 1988, 14(1): 46–52. |
| [5] | Tawfik A, Eid A M, Hasanen R, et al. Q-value customized ablation (custom-Q) versus wavefront optimized ablation for primary myopia and myopic astigmatism[J]. International Ophthalmology, 2014, 34(2): 259–262. DOI: 10.1007/s10792-013-9828-1 |
| [6] | 于秋菊, 张海东, 张永红. 飞秒激光辅助Q值调整的非球面个性化LASIK与常规LASIK术后视觉质量对比研究[J]. 中国实用眼科杂志, 2016, 34(3): 258–262. DOI:10.3760/cma.j.issn.1006-4443.2016.03.013 |
| [7] | Villa C, Gutierrez R, Jimenez J, et al. Night vision disturbances after successful LASIK surgery[J]. British Journal of Ophthalmology, 2007, 91(8): 1031–1037. DOI: 10.1136/bjo.2006.110874 |
| [8] | Kung J S, Manche E E. Quality of vision after wavefront-guided or wavefront-optimized LASIK:a prospective randomized contralateral eye study[J]. Journal of Refractive Surgery, 2016, 32(4): 230–236. DOI: 10.3928/1081597X-20151230-01 |
| [9] | Liou H L, Brennan N A. Anatomically accurate, finite model eye for optical modeling[J]. Journal of the Optical Society of America A, 1997, 14(8): 1684–1695. DOI: 10.1364/JOSAA.14.001684 |
| [10] | Atchison D A. Optical models for human myopic eyes[J]. Vision Research, 2006, 46(14): 2236–2250. DOI: 10.1016/j.visres.2006.01.004 |
| [11] | Navarro R, Santamaría J, Bescós J. Accommodation-dependent model of the human eye with aspherics[J]. Journal of the Optical Society of America A, 1985, 2(8): 1273–1280. DOI: 10.1364/JOSAA.2.001273 |
| [12] | Masalehdan H, Lotfi E, Lotfi A, et al. Modeling of Zernike optical aberrations by MTF and PSF[J]. Biomedical Optics Express, 2010, 18(5): 5245–5248. DOI: 10.1364/OE.18.005245 |
| [13] | Atchison D A, George S B. Optics of the human eye[M]. Oxford: Butterworth, 2000. |
| [14] | 王雁. 波前像差与临床视觉矫正[M]. 北京: 人民卫生出版社, 2011. |
| [15] |
王洁梅. 基于Zernike多项式的波前像差研究[J].
现代计算机, 2014(2): 46–49.
WANG Jiemei. Research on wavefront aberration based on Zernike polynomials[J]. Modern Computer, 2014(2): 46–49. DOI: 10.3969/j.issn.1007-1423(z).2014.02.012 |


