近年来,随着数字化信号处理技术的发展,数字化信号处理方法在核辐射能谱测量系统的信号处理中相较于模拟电路信号处理方法诸如系统灵活性提升、后端通信抗干扰能力提升等优势逐渐显现出来[1-2]。因而使得数字化核信号能谱采集处理系统得到了广泛的研究和应用。
在核电子学的信号处理中,除了要求脉冲信号具有较高的信号噪声比以外,还对脉冲信号的形状有一定的要求:例如希望信号波形较窄而减少信号的重叠和堆积概率,以利于高计数率的使用场景;希望信号顶部平坦而便于脉冲幅度提取分析[3-5]。在核信号处理过程中往往通过带有成形功能的滤波器对辐射探测器输出脉冲信号进行滤波成形处理,以满足上述脉冲信号在形状和信噪比方面的需求[6]。传统的模拟电路能谱测量系统中,CR-RCm滤波器因其性能优越、原理及其实现简单等优点而得到极其广泛的应用,从而使其成为核信号能谱分析领域中一种经典的成形滤波器[7]。本文将以模拟电路CR-RCm滤波器为基础,探讨CR-RCm滤波器的数字化方法,并在此基础上分析数字化CR-RCm滤波器的频率特征及滤波器的滤波成形效果,最终通过实验测试数字化CR-RCm滤波器在能谱测量过程中对能谱全能峰分辨率影响。
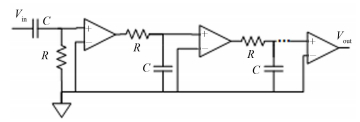
1 滤波器成形算法推导核信号能谱分析系统中,CR高通滤波器可以作为前置放大器的后接白化滤波器,而RC低通滤波器可以作为白化滤波器的近似匹配滤波器[8]。核信号能谱测量系统中常用的模拟CR-RCm滤波电路原理如图 1所示。
|
图 1 CR-RCm滤波器原理图 Figure 1 Schematic of CR-RCm filter. |
图 1的CR-RCm滤波电路本质上是由一个CR高通滤波器和m个RC低通滤波器串联组合而成。因此在进行滤波器数字化处理时,可以利用分而治之的思想:将滤波器进行拆分,分别对拆分后的CR高通滤波器和RC低通滤波器进行数字化处理。
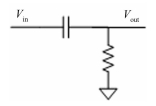
对于图 2所示的CR高通滤波器,根据吉尔霍夫电压电流定律可以推导出该滤波器输入输出电压之间满足线性常系数微分方程如式(1)。
| $RC\frac{{{\rm{d}}y(t)}}{{{\rm{d}}t}} + y(t) = RC\frac{{{\rm{d}}x(t)}}{{{\rm{d}}t}}$ | (1) |
式中:y(t)表示输出信号Vout(t);x(t)表示输入信号Vin(t)。
|
图 2 CR高通滤波器 Figure 2 CR high-pass filter. |
对于经过高速模数变换器(Analog-to-digital Converter, ADC)实时模数变换后的离散数字化信号序列y[n]和x[n],可以将式(1) 进行改写,得到如下所示结果:
| $RC\frac{y[n]-y[n-1]}{T}+y[n]=RC\frac{x[n]-x[n-1]}{T}$ | (2) |
式中:T为高采样率模数变换器的实时采样周期。对式(2) 整理可以得到:
| $y[n]=d\cdot (x[n]-x[n-1])+d\cdot y[n-1]$ | (3) |
式中:d=RC/(RC+T)。由式(3) 可以看出,数字化CR高通滤波器是一个递归型的数字滤波器,这与Smith[9]提出的数字化CR滤波器方案相符。
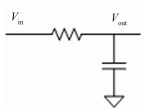
同理,对图 3所示的RC低通滤波器可以写出其输入输出电压之间的线性常系数微分方程:
| $RC\frac{dy(t)}{dt}+y(t)=x(t)$ | (4) |
|
图 3 RC低通滤波器 Figure 3 RC low-pass filter. |
进而可以根据式(4) 得到RC低通滤波器数字化离散输入输出数字信号序列y[n]和x[n]之间的关系如下:
| $y[n]=(1-d)\cdot x[n]+d\cdot y[n-1]$ | (5) |
式(5) 中同样满足d=RC/(RC+T)。对式(3) 和(5) 分别进行Z变换可得CR高通、RC低通滤波器输入输出信号在Z域的关系如下:
| $Y(z)=d\cdot (X(z)-{{z}^{-1}}\cdot X(z)+{{z}^{-1}}\cdot Y(z))$ | (6) |
| $Y(z)=(1-d)\cdot X(z)+d\cdot {{z}^{-1}}Y(z)$ | (7) |
对式(6) 和(7) 进行整理,分别可得到数字化CR高通滤波器和RC低通滤波器在Z域的系统传递函数如下:
| $H(z)=\frac{Y(z)}{X(z)}=\frac{d\cdot (1-{{z}^{-1}})}{1-d\cdot {{z}^{-1}}}$ | (8) |
| $H(z)=\frac{Y(z)}{X(z)}=\frac{1-d}{1-d\cdot {{z}^{-1}}}$ | (9) |
根据传递系统传递函数式(8) 和(9) 可画出数字化CR-RCm滤波器的算法级联框图如图 4所示。

|
图 4 CR-RCm滤波器算法级联框图 Figure 4 Block diagram of CR-RCm filter cascade ladder. |
为了进一步讨论滤波器的频率响应特征,需得到滤波器的频率响应函数。对式(3) 进行离散傅里叶变换,得数字化CR高通滤波器频率响应函数如式(10),利用欧拉公式[10]对其化解整理得式(11):
| $H({{\text{e}}^{jw}})=\frac{Y({{\text{e}}^{jw}})}{X({{\text{e}}^{jw}})}=\frac{d\cdot (1-{{\text{e}}^{-jw}})}{1-d\cdot {{\text{e}}^{-jw}}}$ | (10) |
| $H({{\text{e}}^{jw}})=\frac{d\cdot (1-\cos (w)+j\cdot \sin (w))}{1-d\cdot \cos (w)+j\cdot d\cdot \sin (w)}$ | (11) |
式中:w为分量信号角频率。对式(11) 取模得:
| $|H({{\text{e}}^{jw}})|=|\frac{d\cdot \sqrt{2-2\cos (w)}}{\sqrt{1+{{d}^{2}}-2d\cos (w)}}|$ | (12) |
同理,可对式(5) 进行离散傅里叶变换,得数字化RC低通滤波器的频率响应函数及其模如下:
| $H({{\text{e}}^{jw}})=\frac{1-d}{1-d\cdot \cos (w)+j\cdot d\cdot \sin (w)}$ | (13) |
| $|H({{\text{e}}^{jw}})|=|\frac{1-d}{\sqrt{1+{{d}^{2}}-2d\cos (w)}}|$ | (14) |
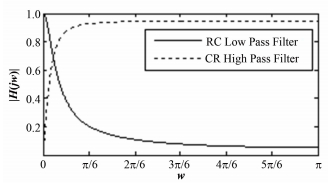
为了验证数字化CR高通和RC低通滤波器的频率响应特征,利用MATLAB工具对式(12) 和(14) 进行模拟,得到如图 5所示的频率响应曲线。
|
图 5 数字化CR和RC滤波器频率响应曲线 Figure 5 Frequency response curves of digital CR and RC filter. |
数字化CR-RCm滤波器的频率响应函数可以通过一个CR滤波器频率响应函数式(11) 和m个RC滤波器频率响应函数式(13) 相乘而得。
| $H({{\text{e}}^{jw}})=\frac{{{(1-d)}^{m}}\cdot d\cdot (1-\cos (w)+j\cdot \sin (w))}{{{(1-d\cdot \cos (w)+j\cdot d\cdot \sin (w))}^{m+1}}}$ | (15) |
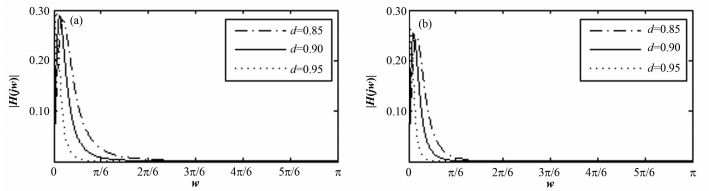
根据式(15) 可以绘制出3级和4级CR-RCm的频率响应曲线,如图 6所示。
|
图 6 CR-RC3 (a)和CR-RC4 (b)滤波器频率响应曲线 Figure 6 Frequency response curves of CR-RC3 (a) and CR-RC4 (b) filter. |
由图 6可知,数字化CR-RCm滤波器的频率响应曲线具有通带滤波器的特征。其中:m和d均可以调节滤波器的通带区域,且m、d越大,通带区域越窄,m的变化对通带区域的影响大于参数d。
3 实验测试为了测试数字化CR-RCm滤波器对脉冲信号滤波成形的效果及滤波成形前后不同脉冲信号对能谱测量中全能峰能量分辨率的影响。利用MATLAB工具和图 4的算法级联框图建立了数字化CR-RCm的滤波器,并利用该数字化滤波器对图 7所示系统采集得到的数字化脉冲信号进行滤波成形。

|
图 7 实验测量系统 Figure 7 Block diagram of experimental test system. |
图 7所示的测量系统探测器部分采用日本滨松公司的碘化钠探测器CH282-01;适配电路(Adapter circuit)采用美国亚德诺半导体公司(Analog Devices Inc, ADI)的差分放大器AD8331;ADC采用美国ADI公司的AD9255(有效位数为12 bit)芯片;数字信号处理芯片采用美国Altera公司经济型现场可编程逻辑门阵列(Field-Programmable Gate Array, FPGA)芯片EP3C40F484C8N。其中包括适配电路、ADC和FPGA在内的信号数字化采集系统可集成在一块10cm×5cm的印刷电路板(Printed Circuit Board, PCB)上,降低了整个系统的面积和体积。
探测器输出的脉冲信号经过数字化采集系统甄别后保留下有效的数字化脉冲信息,并将有效数字化脉冲传递给后端的电脑;在电脑上进行脉冲信号滤波成形和信号有效信息提取分析;最终得到探测器测量得到的能谱。
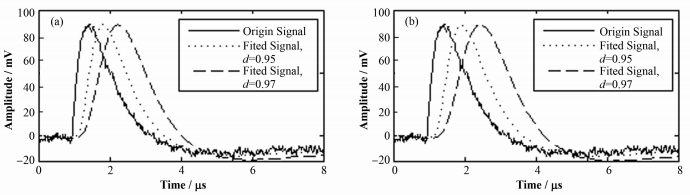
图 8是不同参数m、d的数字化CR-RCm滤波器对图 7系统中高速ADC直接采样后的脉冲信号(即原始核脉冲)滤波成形前后的脉冲信号。
|
图 8 CR-RC3 (a)和CR-RC4 (b)滤波器滤波成形效果 Figure 8 Filter shaping effects of CR-RC3 (a) and CR-RC4 (b) filter. |
表 1为利用上述滤波成形前后的不同脉冲信号测量137Cs能谱所得到的137Cs放射源能谱611 keV全能峰能量分辨率。
| 表 1 不同脉冲信号能谱137Cs全能峰分辨率 Table 1 137Cs's full peak resolution of different signal. |
由表 1实验结果可知,数字化CR-RCm滤波器的级数(即m值)或时间调节参数值d越大,经过滤波器滤波成形后的脉冲信号能谱全能峰分辨率越高;且增加滤波器级数m值对能量分辨率的影响大于增加时间参数d值的影响。
然而随着数字化滤波器级数m的增加,滤波器工程实现的复杂程度也增加;并且随着滤波器时间调节参数值d或滤波器级数m的增加,滤波器滤波成形后脉冲信号越宽,越容易造成脉冲堆积[11]。因此在实际应用中,应该根据实际应用场景中能量分辨率和脉冲计数率两方面的需求来综合考虑,选择符合工程应用需求的滤波器参数值。
4 结语从基本的CR高通和RC低通滤波电路输入输出间电压满足的线性常系数微分方程关系出发,推导出数字化CR高通和RC低通滤波器的输入输出离散化数字信号序列之间满足的递归方程式,并基于此方程式利用Z变换导出了数字化CR高通和RC低通滤波器的在Z域的传递函数。在以上工作的基础上进一步推导出数字化CR-RCm滤波器的Z域传递函数及频率响应函数,并从时域和频域的角度分析了滤波器的性能特征。最终通过实验测试了数字化CR-RCm滤波器在数字化能谱测量系统中对能量分辨率的提升效果。将模拟核电子学中的经典CR-RCm滤波器成形电路数字化,具有较大的参考价值和工程应用促进作用。
本文提供的模拟滤波器数字化分析方法以及提出的数字化CR高通滤波器和RC低通滤波器对将来更加复杂的核信号数字化滤波成形算法研究有着借鉴意义。
| [1] |
袁超, 李勇平, 黄跃峰. 裂变室输出信号数字化处理的仿真研究[J].
核技术, 2015, 38(1): 010401.
Ch ao, LI Yongping, HUANG Yuefeng. Simulation study on digital processing of fission chamber output signal[J]. Nuclear Techniques, 2015, 38(1): 010401. DOI: 10.11889/j.0253-3219.2015.hjs.38.010401 |
| [2] |
李伟男, 杨朝文, 周荣. 基于FPGA脉冲幅度分析器的数字化基线估计方法[J].
核技术, 2015, 38(6): 060403.
LI Weinan, YANG Chaowen, ZHOU Rong. Baseline estimation method of digital multi-channel pulse height analyzer based on FPGA[J]. Nuclear Techniques, 2015, 38(6): 060403. DOI: 10.11889/j.0253-3219.2015.hjs.38.060403 |
| [3] |
洪旭, 倪师军, 周建斌, 等. 数字高斯脉冲成形算法仿真研究[J].
核技术, 2016, 39(11): 110403.
X u, NI Shijun, ZHOU Jianbin, et al. Simulation study on Gaussian pulse shaping algorithm[J]. Nuclear Techniques, 2016, 39(11): 110403. DOI: 10.11889/j.0253-3219.2016.hjs.39.110403 |
| [4] |
陈小猛, 张羽中, 艾宪芸, 等. 数字多道脉冲幅度分析器中数字Dither加入方法[J].
核技术, 2015, 38(5): 050401.
CHEN Xiaomeng, ZHANG Yuzhong, AI Xianyun, et al. Method of digital Dither adding for digital multi-channel pulse amplitude analyzer[J]. Nuclear Techniques, 2015, 38(5): 050401. DOI: 10.11889/j.0253-3219.2015.hjs.38.050401 |
| [5] |
杨振雷, 王晓辉, 苏弘, 等. 一种Flash型FPGA单粒子效应测试方法设计及验证[J].
核技术, 2015, 38(2): 020404.
YANG Zhenlei, WANG Xiaohui, SU Hong, et al. Design and verification of test method for the single event effect in Flash-based FPGA[J]. Nuclear Techniques, 2015, 38(2): 020404. DOI: 10.11889/j.0253-3219.2015.hjs.38.020404 |
| [6] | Glenn K F. Radiation detection and measurement[M]. 4th ed. John Wiley & Sons, 1989:625-641. |
| [7] | Nakhostin M. Recursive algorithm for real-time digital CR-(RC)n pulse shaping[J]. IEEE Transactions on Nuclear Science, 2011, 58(5): 2378–2381. DOI: 10.1109/TNS.2011.2164556 |
| [8] | Kalinin A I, Bednyakov V A. Pulse shaping for Ge-spectrometers optimized for ballistic deficit and electronic noise[J]. Nuclear Instruments & Methods in Physics Research, 2005, 538(538): 718–722. DOI: 10.1016/j.nima.2004.08.126 |
| [9] | Smith S W. The scientist and engineer's guide to digital signal processing[M]. California Technical Publishing, 1997:322-325. |
| [10] | Shastri A R, Anant R. Basic complex analysis of one variable[M]. Bombay: Department of Mathematics, Indian Institute of Technology, 2010: 16-18. |
| [11] |
张怀强, 吴和喜, 汤彬, 等. 数字核谱仪系统中脉冲堆积识别方法的研究[J].
东华理工大学学报(自然科学版), 2012, 35(3): 281–284.
ZHANG Huaiqiang, WU Hexi, TANG Bin, et al. Methods of pulse pile-up identification in digital nuclear spectrometer system[J]. Journal of East China Institute of Technology (Natural Science), 2012, 35(3): 281–284. DOI: 10.3969/j.issn.1674-3504.2012.03.013 |


