2. 中国科学院大学 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
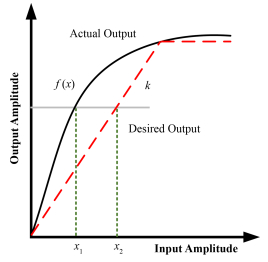
自由电子激光大多数是利用电子直线加速器产生的电子束团来产生的,被称为第四代同步辐射光源。上海软X射线自由电子激光装置作为国内第一台第四代光源[1],对电子束团的能量稳定性、能散度提出了很高的要求,这就要求高频低电平控制系统对各个速调管的输出信号进行精确的测量和控制,以保证加速器的稳定运行并且达到其技术指标。在软X射线自由电子激光(Soft X-ray Free-electron Laser, SXFEL)直线加速器中,速调管工作在近饱和区的工作点[2],其输入输出振幅特性是非线性的,如图 1中实线所示。
|
图 1 速调管输入输出振幅特性的原理 Figure 1 Schematic of the klystron amplitude output characteristics. |
然而由于环境温度等因素的影响会导致工作点的漂移,而此时由于速调管的非线性放大特性,在近饱和区的工作点,输入信号的幅度变化,很难引起相应的输出信号的幅度变化,这就降低了反馈控制的有效性,造成了微波低电平(Low Level Radio Frequency, LLRF)控制调节系统的低效率性[3]。所以,我们需要在SXFEL直线加速器的低电平控制系统中建立一种在线系统[4],跟踪补偿速调管带来的非线性问题,使其反馈增益一致,如图 1中虚线所示,以此来提高低电平控制系统的反馈精度。
目前,国际上许多自由电子激光装置都对其速调管装置进行了线性化的设计。使用的方法有模拟方法、数字方法、反馈技术、前馈技术、预失真技术以及基于不同的硬件数字信号处理技术(Digital Signal Process, DSP)、现场可编程门阵列(Field Programmable Gate Array, FPGA)等[5]。模拟方法设备复杂、不够灵活,数字方法更加的准确以及有更好的适应性。长反馈会有延时,特别是在脉冲状态工作时,束流负载突然改变需要补偿时。前馈方法则很复杂,需要集成在系统中。基于每一种解决方法的特点以及现有的微波低电平控制系统结构,预失真方法是最符合我们预期的。
随着国内自由电子激光研究的发展,对速调管线性化系统的设计也变得越发迫切。本文介绍了针对于SXFEL实验装置设计的速调管线性化系统。
1 方案的设计软X射线自由电子激光装置使用基于微型电信计算构架(Micro Telecom Computing Architecture, MTCA)系统架构的低电平控制系统,系统采用FPGA作为数字信号处理和控制算法的硬件平台,可编程芯片采用XILINX Virtex6处理器XC6VLX130T。
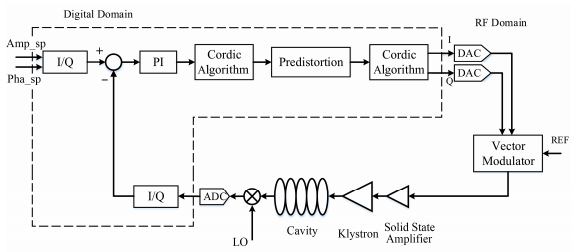
图 2展示了SXFEL装置的低电平控制系统的结构。电子直线加速器的微波功率源系统使用分布式控制方案,每台速调管处安装一台低电平控制系统,用于测量射频(Radio Frequency, RF)信号。在本地的低电平控制系统中读取测量得到的RF信号值,计算出测量信号与给定值之间的偏差,通过偏差值来控制PI控制器,调整正交(In-phase Quadrature, IQ)调制器的输出信号,完成对幅度相位的控制[6-7]。
|
图 2 低电平控制系统的结构框图 Figure 2 Schematic of the low level RF control system. |
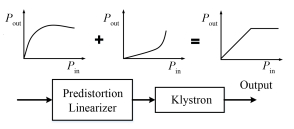
由此,针对于SXFEL实验装置设计的速调管输入输出特性曲线的线性化系统,采用基于FPGA的数字预失真算法[8]。如图 2所示,即在低电平控制系统中引入一个与速调管非线性放大特性相反特性的前置畸变放大器模块,来补偿速调管非线性放大的特性。其预失真线性化方案原理如图 3所示。
|
图 3 预失真线性化方案原理 Figure 3 Typical predistortion linearization scheme. |
采用数字预失真方法需要对速调管的非线性特性进行精确的测量以此来计算出与之特性相反的预失真模块。
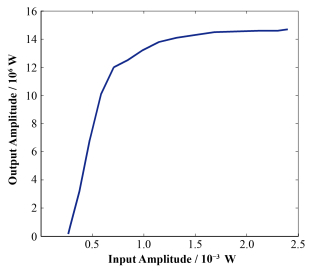
2 速调管非线性放大特性的实验测量与建模 2.1 速调管非线性放大特性的实验测量通过实验,分析由速调管引起的非线性特性,实验依托于SXFEL装置,使用Toshiba 50 MV 2856MHz速调管,实验测得的速调管输入输出特性曲线(以30 kV高压下测得数据为例)见图 4。
|
图 4 测量所得速调管输入输出特性曲线 Figure 4 Measurements of the input to output characteristic of the klystron. |
可观察到,随着输入信号的增大,输出功率刚开始时,呈线性增长,后来输出功率的增益会越来越小,输出功率慢慢趋于饱和。
2.2 速调管非线性放大特性的建模系统需要对实验测得的速调管非线性放大曲线建模,提取速调管功放模型,以此来进行仿真模拟,进而求出预失真函数,并对其建模。速调管输入输出特性曲线是非线性的,目前用于非线性建模的方法主要有:多项式法、Voletrra级数法、神经网络法等。本文建模采用了两种模型:Rapp模型[9]以及传统多项式模型。
2.2.1 Rapp模型Rapp模型于1980年提出[10],是一种用于描述功率放大器的输入输出关系的常用和经典的模型,模型中共有p0、p1、p2、p3参数,通过输入测量值,求得这4个参数,可得到速调管的转移特性,其表达式为:
| ${{A}_{\text{out}}}=f({{A}_{\text{in}}})=\frac{{{p}_{1}}{{A}_{\text{in}}}+{{p}_{2}}}{\sqrt{1+{{\left( \frac{{{A}_{\text{in}}}}{{{p}_{0}}} \right)}^{2}}}}+{{p}_{3}}$ | (1) |
式中:Ain表示功率放大器的输入;Aout表示功率放大器的输出。
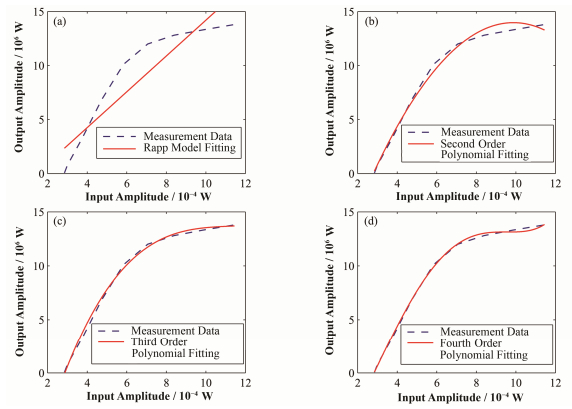
2.2.2 传统多项式模型图 5展示了分别采用了Rapp模型、二阶多项式模型、三阶多项式模型、四阶多项式模型进行模拟的速调管输入输出特性曲线。
| $\begin{align} &{{A}_{\text{out}}}=f({{A}_{\text{in}}}) \\ &={{p}_{k}}{{x}^{k}}+{{p}_{k-1}}{{x}^{k-1}}+\cdots +{{p}_{1}}x+{{p}_{0}} \end{align}$ | (2) |
|
图 5 原始测量值与多种模型拟合 (a) Rapp模型拟合,(b)二阶多项式拟合,(c)三阶多项式拟合,(d)四阶多项式拟合 Figure 5 Klystron output measurement data vs. model fitting. (a) Rapp model fitting, (b) Second order polynomial fitting, (c) Third order polynomial fitting, (d) Fourth order polynomial fitting |
由图 5分析可知,图 5(a)所示的Rapp拟合,由于拟合的是激励通路的输入输出特性,包含一个功率放大器和速调管,速调管作为一个超大功率放大器,二者的非线性的组合,使得输入和输出放大的倍数达到了100 dB,导致了Rapp模型的不适用。再通过拟合优度公式:
| $\text{Fit}=1-\frac{\sum{{{(V(i)-{{V}_{m}}(i))}^{2}}}}{\sum{{{(V(i)-{{V}_{p}}(i))}^{2}}}}$ | (3) |
式中:V(i)表示测量值;Vm(i)表示模拟值;Vp(i)表示测量值的平均值。可定量地计算出4种拟合方式的拟合优度。Rapp模型、二阶多项式模型、三阶多项式模型、四阶多项式模型拟合优度分别为:0.854220666892191、0.993063918064978、0.997510603706864、0.999249942906822。可见,多项式模型阶数越高,拟合优度数值越大,越接近于1,拟合越精确。综合考虑,我们选取三阶多项式模型作为速调管输入输出特性曲线的建模模型。
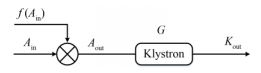
3 预失真函数的模拟 3.1 多项式预失真算法图 6为多项式预失真算法原理。输入振幅Ain通过乘以一个关于Ain的多项式修正因子f(Ain),得到预失真模块输出Aout。Aout再作为速调管的输入,通过非线性特性的速调管;G表示速调管的非线性特性,最终使得速调管输入与输出的特性曲线为线性;Kout表示速调管的输出。
|
图 6 多项式预失真算法速调管线性化的原理 Figure 6 Schematic of the polynomial-based klystron linearization algorithm. |
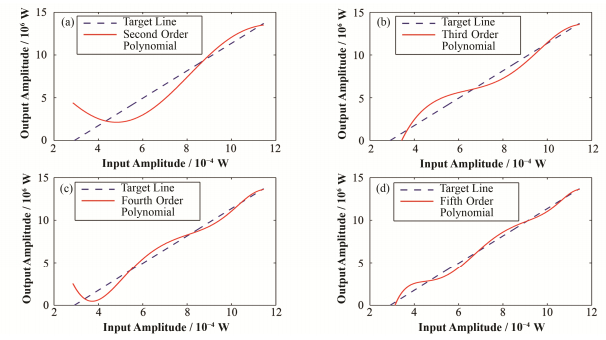
图 7展示了分别使用二阶、三阶、四阶、五阶多项式预失真算法后经过前面采用的三阶多项式拟合的速调管非线性特性得到的MATLAB仿真的线性化结果。可以观察到,多项式预失真算法可以起到线性化的作用,但是还存在一定的误差。虽然随着多项式函数阶数的增加,拟合会越来越精确,误差也会越来越小。但是在输入较小时,存在的误差还是比较大的,这是多项式预失真补偿算法的通病。
|
图 7 多项式预失真算法实现后的线性化结果与线性化目标函数 (a)二阶多项式预失真算法,(b)三阶多项式预失真算法,(c)四阶多项式预失真算法,(d)五阶多项式预失真算法 Figure 7 Polynomial-function-based linearization vs. target line. (a) Second order polynomial-function, (b) Third order polynomial-function, (c) Fourth order polynomial-function, (d) Fifth order polynomial-function |
直接查找表(Lookup Table, LUT)预失真算法原理如图 1所示:f(x)为实际的非线性放大曲线;y=kx表示理想的线性化输出函数。设所求预失真函数为g(x),则f(g(x))=kx,由f(x1)=kx2可得:
| ${{x}_{2}}=\frac{1}{k}f({{x}_{1}})$ | (4) |
由此可知,预失真函数g(x)即为x1与x2的对应关系。此关系式可使用查找表存储,x1表示预失真函数的输出,x2表示预失真函数的输入。
预失真函数上的点是无数的,但是查找表不能是无限大的,所以查找表算法会设置节点,将预失真函数的输出均分为节点数份数,并通过式(4) 计算出每一个节点对应的预失真函数的输入值。当输入功率大于上一个节点对应的预失真函数的输入值、小于这一节点对应的预失真函数的输入值时,那么将这一范围内的输入,对应的预失真函数的输出全部定为节点值。由此看出,使用直接查找表算法,得到的线性化曲线会是阶梯状的。当然,节点越多,阶梯越多,预失真函数的精度也就越高,线性化程度也会越好,但同时查找表也会越大,查找越复杂,也意味着所需的存储空间越大。
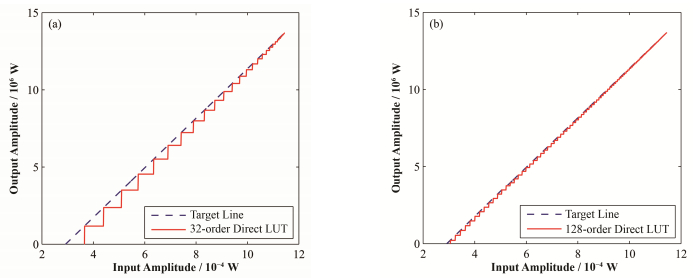
图 8展示了分别使用设置了32个节点和128个节点的查找表预失真算法后经过前面采用的三阶多项式拟合的速调管非线性特性得到的MATLAB仿真的线性化结果。由图 8可见,32个节点的查找表预失真算法线性化结果共有32个阶梯,有明显的阶梯状,在输入较小时,误差比较明显,随着输入的增加,误差越来越小。128个节点的查找表预失真算法线性化结果则共有128个阶梯,相比于32个节点,线性化程度更好,误差更小,随着输入的越来越大,几乎为线性。
|
图 8 直接查找表算法实现后的线性化结果与线性化目标函数 (a) 32个节点,(b) 128个节点 Figure 8 Direct lookup table function-based linearization vs. target line. (a) 32-knot, (b) 128-knot |
由§3.2.1可知,查找表预失真算法的误差主要是由一定范围的输入对应的预失真函数的输出都为同一个节点值而造成的,虽然不断地增大节点数,可以使得阶梯越来越接近直线,但这样会耗费更多的资源,由此,在直接查找表算法的基础上引入线性差值的概念,就得到了插值法查找表算法,即输入的每一点对应的预失真函数的输出不再是其对应的节点处的值,而是节点值加上节点处的斜率乘以该点的输入与节点对应的输入的差值。这样输入的每一点对应的输出都不再相同,线性化后的结果将不再是阶梯状的,大大提高了线性化的精度[11]。
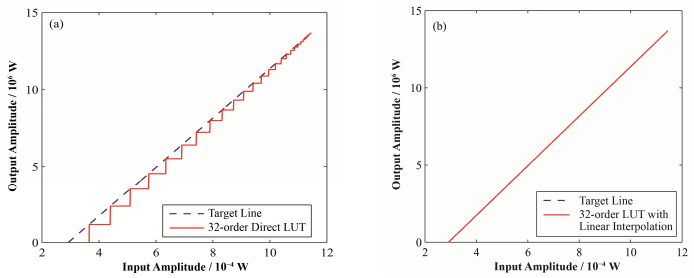
图 9展示了32个节点的直接和插值法查找表预失真算法的线性化结果。可明显看出,在同为并不是很多的节点,插值法查找表预失真算法,相较于直接查找表预失真算法,线性化程度更高,几乎为一条直线。
|
图 9 32个节点的直接(a)和插值法(b)查找表算法实现后的线性化结果与线性化目标函数 Figure 9 32-knot direct lookup table function-based (a) and 32-knot lookup table with linear interpolation-based (b) linearization vs. target line. |
多项式预失真算法虽然没有查找表,会节省内存资源,但算法复杂,且在输入较小时,存在较大的误差,总体上线性化结果不是很好。直接查找表方法简单、易于实现、速度快,但会占用较大内存,插值法查找表具有和直接查找表一样的优点,并且在这三种算法中线性化结果最好。最终我们选取了插值法查找表算法进行线性化设计。
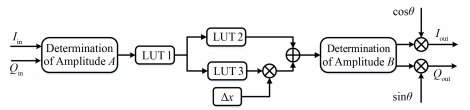
3.4 插值法查找表预失真算法FPGA中的实现图 10展示了插值法查找表算法在FPGA中的实现原理。如§3.2中所述,查找表LUT 1中存储着预失真关系式中的输入x2,查找表LUT 2中存储着预失真关系中的输出x1,查找表LUT 3中存储着节点处的斜率,Δx表示该点的输入与节点对应的输入的差值。低电平系统中输入的Iin和Qin,通过使用ISE Math Functions IP核由公式
|
图 10 插值法查找表预失真算法在FPGA中实现的原理 Figure 10 Schematic of lookup table with interpolation FPGA based predistortion algorithm. |
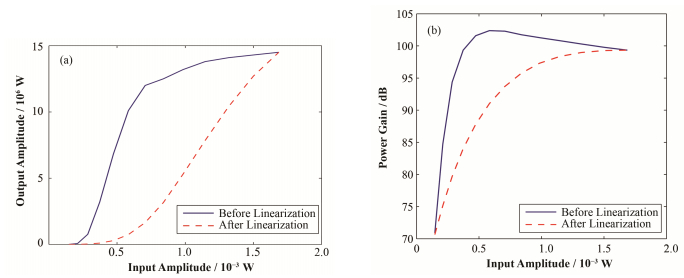
如图 2所示,我们在软X射线自由电子激光的2856 MHz低电平控制系统里面加上插值法查找表预失真模块,用Toshiba速调管E3730A和高压调制器系统进行了实地的高功率测试,在阴极高压30kV的情况下,进行了上机验证,记录速调管输入输出功率数据。图 11展示了速调管线性化结果和功率增益。
|
图 11 比较速调管线性化前后的输入输出(a)和功率增益(b) Figure 11 Compare the input to output characteristic (a) and the power gain (b) of the klystron before and after linearization. |
可观察到,在上机验证中,经过FPGA量化、机器噪声、现场干扰等因素,最终得到的线性化曲线与仿真的线性化结果有一定的误差,但使用插值法查找表算法设计的预失真模块仍然对速调管的非线性输入输出进行了很好的线性化,修正后速调管的功率增益曲线没有了修正之前的大幅变化,比较平滑,可以满足SXFEL低电平控制系统的需求,极大地提高了其控制性能。
5 结语自由电子激光中的低电平控制系统是保证直线加速器加速管稳定性的关键因素,对获得高增益、高亮度的自由电子激光有着非常重要的意义。本文所阐述的基于低电平控制系统的在线速调管输入输出功率线性化系统,使用基于插值法查找表的预失真方法,使得速调管的输入输出具有良好的线性度,提高了微波低电平系统的调节精度和准确性,改善了高频低电平系统的性能,满足了上海软X射线自由电子激光试验装置的需求,并具有可移植性,为下一步在不同高压下的自适应线性化调节研究打下了坚实的基础。
| [1] | Zhao Z T, Chen S Y, Yu L H, et al. Shanghai soft X-ray free electron laser test facility[C]. Proceedings of IPAC2011, San Sebastián, Spain, 2011:3011-3013. |
| [2] | Rezaeizadeh A. Automatic control strategies for the Swiss free electron laser[D]. Switzerland:Automatic Control Laboratory, 2016. |
| [3] | Omet M, Michizono S, Matsumoto T, et al. FPGA-based klystron linearization implementations in scope of ILC[J]. Nuclear Instruments and Methods in Physics Research, 2015, A780: 1–8. DOI: 10.1016/j.nima.2015.01.056 |
| [4] | Cichalewski W, Koseda B. Characterization and compensation for nonlinearities of high-power amplifiers used on the FLASH and XFEL accelerators[J]. Measurement Science and Technology, 2007, 18(8): 2372. DOI: 10.1088/0957-0233/18/8/011 |
| [5] | Katz A. Linearization:reducing distortion in power amplifiers[J]. IEEE Microwave Magazine, 2001, 2(4): 37–49. DOI: 10.1109/6668.969934 |
| [6] |
李林. 软X射线自由电子激光LLRF控制系统建模及算法研究[D]. 上海: 中国科学院上海应用物理究所, 2015.
LI Lin. RF system modeling and research on algorithm of digital low level RF system of soft X-ray free electron lasers[D]. Shanghai:Shanghai Institute of Applied Physics, Chinese Academy of Sciences, 2015. |
| [7] |
张俊强, 殷重先, 高永强, 等. FPGA实现次谐波聚束器的幅相控制[J].
核技术, 2012, 35(7): 499–502.
ZHANG Junqiang, YIN Chongxian, GAO Yongqiang, et al. Energy feedback control for Linac of SSRF[J]. Nuclear Techniques, 2012, 35(7): 499–502. |
| [8] | Zeng R, McGinnis D, Molloy S. Control performance improvement by using feedforward in LLRF[C]. Proceedings of IPAC 2012, New Orleans, Louisiana, USA, 2012. |
| [9] | Rapp C. Effects of HPA-nonlinearity on a 4-DPSK/OFDM-signal for a digital sound broadcasting signal[C]. European Conference on Satellite Communications, Liege, Belgium, 1991:179-184. |
| [10] | Cann A. Nonlinearity model with variable knee sharpness[J]. IEEE Transactions on Aerospace and Electronic Systems, 1980(6): 874–877. DOI: 10.1109/TAES.1980.309016 |
| [11] | Omet M, Michizono S, Matsumoto T, et al. Development of FPGA-based predistortion type linearization algorithms for klystrons within digital LLRF control systems for ILC-like electron accelerators[C]. Proceedings of LINAC 2014, Geneva, Switzerland, 2014. |


