2. 中国核动力研究设计院 信息中心 成都 610213
2. Center of Information, Nuclear Power Institute of China, Chengdu 610213, China
核设施退役是一项周期长、涉及面广、投资高的系统工程,基于安全性、经济性、合理性的考虑,在实施各项核设施退役工作前,必须借助计算机仿真手段对退役技术方案和关键步骤进行验证、评估和演练,优化拆除工艺,以降低对人员和环境的危害。
国际上对核设施退役仿真系统进行了广泛和深入的研究。法国原子能委员会 (French Atomic Energy Commission, CEA)[1]开发了基于虚拟现实技术框架与点核积分方法的NARVEOS系统。该软件支持情景设计、快速剂量计算,是适用于核辐射评估的ALARA (As Low As Reasonably Achievable) 分析工具。经济合作与发展组织核能局 (Nuclear Energy Agency, Organization for Economic Co-operation and Development, OECD/NEA)、日本原子力科学研究机构 (Japan Atomic Energy Agency, JAEA) 和哈尔登 (Halden) 反应堆工程中心[2]共同研发了一套人员剂量评估系统VRDose,可实现评估剂量、优化退役计划等功能。韩国原子能研究所和忠南大学[3]联合对韩国KRR-1 & 2反应堆退役开展工人辐射剂量计算机模拟,能实现基于MCNP-4C[4]辐射输运程序下的人的辐射剂量计算。随着我国核能事业的高速发展,对核设施退役技术研究与工程准备工作的要求更加体系化、专业化、标准化。目前,国内已有部分单位在辐射场可视化软件开发和核设施虚拟退役等方面开展了相关研究,取得了较好的成果[5-9],但对于核设施退役中拆除路径最优化方法的研究相对较少且缺乏针对性。本文验证并采用点核积分法重构核设施退役过程中多源项的三维辐射场,然后利用类旅行商问题 (Traveling Salesman Problem, TSP) 数学模型求解核退役拆除路径问题,构造不同拆除路径下所受外照射剂量矩阵,通过遗传算法寻找最优路径。设计开发了软件实现相应功能并进行了实例分析。
1 核退役设施三维辐射场重构定量和可视化描述核退役过程中工作人员所受辐射照射,需要构建核设施的三维辐射场。由于核退役设施一般规模较大、源项较多,利用MCNP软件求解核设施内部辐射场会导致运算时间很长,且难以满足误差要求,因此发展基于点核积分法的核退役设施三维辐射场求解方法。
1.1 点核积分重构三维辐射场点核积分计算核设施退役场所内辐射场分布的方法如下[10]:
| ${\dot{D}} = \int_E {\int_V {\frac{{A(r,E){{\rm{e}}^{ - b}}B\eta }}{{{\rm{4}}\pi {{\left| {r - r'} \right|}^2}}}} } {\rm{d}}V{\rm{d}}E$ | (1) |
式中:
1) 辐射场内其它器件kj(j≠i)可视为点源,则拆除人员在器件ki处受到器件kj(j≠i)的剂量率
| ${{{\dot{D}}}_{{{k}_{i}},{{k}_{j}}}} = \frac{{{A_{{k_j}}}{\Gamma _k}{{\rm{e}}^{ - b}}B}}{{r_{{k_i},{k_j}}^2}}$ | (2) |
式中:Akj是kj号器件的源活度;Γk是比释动能率常数;rki, kj为ki号器件到kj号器件的几何距离。
2) 器件ki应作为体源处理,此时拆除人员受到器件ki的剂量率
| ${{{\dot{D}}}_{{{k}_{i}},{{k}_{i}}}} = \int_{{V_{{k_i}}}} {\frac{{{A_{{k_i}}}}}{{{V_{{k_i}}}}} \times \frac{{{\Gamma _k}{{\rm{e}}^{ - b}}B}}{{{{\left| {r - r'} \right|}^2}}}{\rm{d}}V} $ | (3) |
式中:Vki是器件ki的体积;r和r'分别是ki号器件和拆除人员拆除它时所处的几何位置。
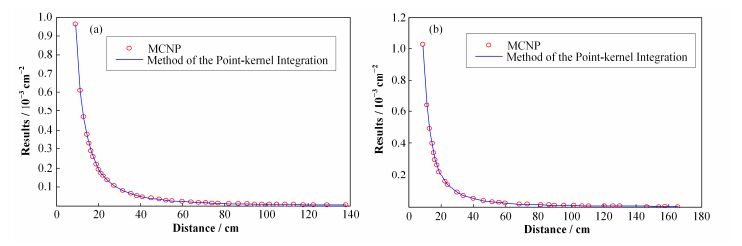
1.2 蒙特卡罗程序校验点核积分结果利用MCNP5验证简单源项情况下点核积分的结果,为简化计算,将结果归一化处理,如图 1所示。其中,图 1(a)是退役设施内为一点源的结果,图 1(b)是核设施内为一立方体源 (10cm×10cm× 10cm) 的结果。从图 1可以发现,点源和体源情况下,点核积分结果都与MCNP计算结果吻合很好。这可在相同计算精度下,大幅节省最优退役拆除路径的搜寻时间。
|
图 1 点源 (a) 和体源 (b) 下的MCNP与点核积分比较结果 Figure 1 Comparison between MCNP and the point-kernel integration when calculating point source (a) and volume source (b). |
核设施内部各处剂量率值
TSP是著名的数学图论问题,应用背景广泛,问题描述如下:旅行商从某城市出发,遍历各城市后返回到出发城市,寻找旅行商所走总距离最小的路线。
在核设施退役模型中,设施内有N个器件,则拆除所有器件的路径有N!条,路径数目随N增加而急剧上升,最优路径的求解难度增加。为得到最优退役拆除路径,将核设施退役拆除路径问题假设成类似TSP问题,特点在于拆除路径起点可不同、可不为闭合回路,即:
1) 退役过程中需拆除的器件作为TSP问题中的城市;
2) 退役过程中的优化目标为工作人员所受总剂量,作为TSP问题中的总路程。由于在设施中行走所需的时间远小于拆除过程所需的时间,忽略工作人员行走中所受剂量。
2.2 不同路径下总剂量的求解假设有N个需拆除的器件,拆除路径为k1,k2,k3,…,kN,其中:ki是第i个被拆除的器件的编号,利用式 (2)、(3) 建立剂量率矩阵DR:
| ${{\mathit{\boldsymbol{D}}}_{\rm{R}}}\rm{=}\left[ \begin{matrix} {{{\dot{D}}}_{{{k}_{1}},{{k}_{1}}}} & {{{\dot{D}}}_{{{k}_{1}},{{k}_{2}}}} & \cdots & {{{\dot{D}}}_{{{k}_{1}},{{k}_{N}}}} \\ {{{\dot{D}}}_{{{k}_{2}},{{k}_{1}}}} & {{{\dot{D}}}_{{{k}_{2}},{{k}_{2}}}} & \cdots & {{{\dot{D}}}_{{{k}_{2}},{{k}_{N}}}} \\ \vdots & \vdots & {} & \vdots \\ {{{\dot{D}}}_{{{k}_{N}},{{k}_{1}}}} & {{{\dot{D}}}_{{{k}_{N}},{{k}_{2}}}} & \cdots & {{{\dot{D}}}_{{{k}_{N}},{{k}_{N}}}} \\ \end{matrix} \right]$ | (4) |
式中:
建立时间矩阵T:
| $\mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {{t_{{k_1}}}} & {{t_{{k_1}}}} & \cdots & {{t_{{k_1}}}}\\ 0 & {{t_{{k_2}}}} & \cdots & {{t_{{k_2}}}}\\ \vdots & \vdots & {} & \vdots \\ 0 & 0 & \cdots & {{t_{{k_N}}}} \end{array}} \right]$ | (5) |
式中:tki为拆除ki号器件所需的时间;矩阵元素Ti, j表示拆除第ki号器件时,kj号器件照射拆除人员的时间。
剂量率矩阵和时间矩阵相乘,得剂量矩阵D,D矩阵各元素求和即为拆除人员受到的总剂量f(x)。
| $f{\rm{(}}x{\rm{) = }}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{\mathit{\boldsymbol{D}}_{i,j}}} } = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {\left( {{\mathit{\boldsymbol{D}}_{{\rm{R}}i,j}} \times {\mathit{\boldsymbol{T}}_{i,j}}} \right)} } $ | (6) |
实际操作中,一个器件可能分多次拆除。该情况下,设定器件单元数M,即一个器件平均分为M个单元,各单元的活度和产生的剂量率为器件的1/M,拆除各单元所需的时间为拆除器件总时间的1/M。设同一器件中各单元位置相同,则同一器件不同单元辐射效果相同。单元总数为MxN个,拆除人员需遍历所有单元。
假设拆除路径为u1, u2, u3, …uNM,其中:up是第p个被拆除单元的编号。建立剂量率矩阵DR:
| ${{\mathit{\boldsymbol{D}}}_{\rm{R}}}\rm{=}\left[ \begin{matrix} {{{\dot{D}}}_{{{u}_{1}},{{u}_{1}}}} & {{{\dot{D}}}_{{{u}_{1}},{{u}_{2}}}} & \cdots & {{{\dot{D}}}_{{{u}_{1}},{{u}_{NM}}}} \\ {{{\dot{D}}}_{{{u}_{2}},{{u}_{1}}}} & {{{\dot{D}}}_{{{u}_{2}},{{u}_{2}}}} & \cdots & {{{\dot{D}}}_{{{u}_{2}},{{u}_{NM}}}} \\ \vdots & \vdots & {} & \vdots \\ {{{\dot{D}}}_{{{u}_{NM}},{{u}_{1}}}} & {{{\dot{D}}}_{{{u}_{NM}},{{u}_{2}}}} & \cdots & {{{\dot{D}}}_{{{u}_{NM}},{{u}_{NM}}}} \\ \end{matrix} \right]$ | (7) |
式中:
| ${{{\dot{D}}}_{{{u}_{p}},{{u}_{q}}}}=\frac{{{{\dot{D}}}_{{{k}_{i}},{{k}_{j}}}}}{M}$ | (8) |
式中:ki为单元up所在器件的编号;kj为单元uq所在器件的编号。拆除每个单元所需的时间tuq=tki/M。构建时间矩阵及计算总剂量同§2.2,实现器件的单元化。
3 遗传算法寻优计算与分析旅行商问题有多种解法,目前较为常用的算法有神经网络法和遗传算法。遗传算法[11]是最近几年发展起来的全局优化算法,借用生物遗传学观点,通过选择、遗传、变异和免疫等作用机制,使每个个体的适应性提高。由于全局搜索的特性,遗传算法解决TSP问题有特定优势。故采用遗传算法求解上述问题,并通过图形用户界面 (Graphical User Interface, GUI) 设计了求解本问题的可视化软件。
3.1 算法流程利用遗传算法求解核退役拆除路径优化问题的步骤如下:
1) 种群初始化
由于核设施问题假设成多目标旅行商问题,个体编码方法采用实数编码。在核设施退役中,将器件组顺序实数编码为1-N(设施内的总器件数)或1-N×M(设施内的总单元数)的随机排列,初始化的参数有种群个数、染色体基因个数、迭代次数Nc、交叉概率Pc以及变异概率Pm。
2) 建立适应度函数
拆除某一器件时所受剂量率由点核积分已知,器件组随机全排列对应的总剂量可求,总剂量越小,种群的适应度函数越好。将总剂量的倒数作为适应度函数,由求min f(x) 变为求max[1/f(x)]。
3) 选择操作
用轮盘赌法和两两竞争的方法进行选择操作,采用基于适应度比例的选择策略,即适应度越好的个体被选择的概率越大,并保存所选适应度最高的个体。
4) 交叉操作
利用部分映射交叉 (Partial Mapped Crossover, PMX) 算法进行交叉操作,先对父代进行常规的两点交叉,再根据交叉区域内各基因值之间的映射关系来修改交叉区域之外的各个基因值,该算法可以较多地产生父代遍历路径所没有的部分新路径,收敛速度较低,但其全局搜索能力较强。
5) 变异操作
对于变异操作,随机选取个体,同时随机选取个体的两个基因进行交换以实现变异操作。
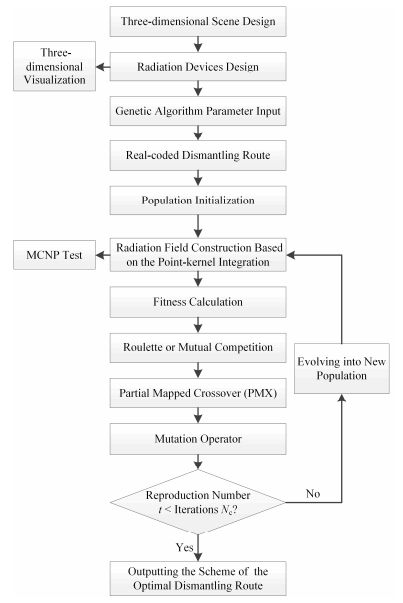
算法整体流程如图 2所示。
|
图 2 求解核设施退役拆除路径优化问题的算法整体流程 Figure 2 Whole algorithm flow chart of solving the dismantling route optimization problem during nuclear decommissioning. |
当核设施内源项个数为1时,不同的器件单元数必然对应同一优化路径。经程序验证发现,源项较少时,不同的器件单元数趋于对应同一优化路径,即单元数为1对应的路径。故源项较少情况下,器件可分多次拆除无明显优势;源项较多时,分多次拆除同一器件的路径较为复杂,为便于观看,建立一个10cm×10cm×10cm的厂房,随机放置30个正方体形状的放射性器件,器件的尺寸在 (1-8)×10-3m3内随机分布,器件的活度在 (1.85-5.5)×1010 Bq内随机分布,假设拆除时间与拆除器件的体积成正比:ti=V/c(其中:V为体积,m3;c为比例系数,以下取c=3为例)。
各器件单元数M=1时,利用MATLAB实现遗传算法求解基于旅行商问题下的最优退役路线如图 3(a)所示,其中初始种群为100个,迭代次数为1000次。由图 3(b)可知,该例中拆除人员的总剂量在迭代200次左右达到收敛,最优路线对应的受照总剂量为9.63×10-10Gy。

|
图 3 单元数M=1时核设施退役拆除优化路径结果 (a) 最优路径图,(b) 遗传算法迭代曲线 Figure 3 Results of dismantling route optimization during nuclear decommissioning when the unit number M=1. (a) Optimal dismantling route, (b) Iteration of genetic algorithm |
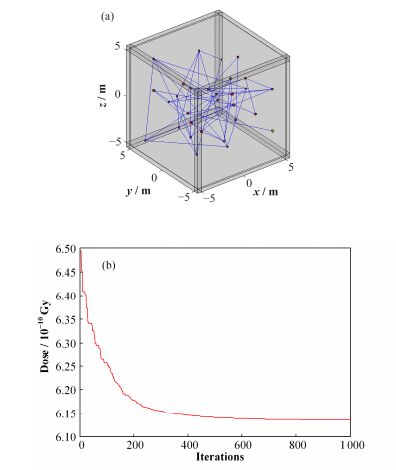
单元数M设为5时,拆除人员可分多次对某一器件进行拆除,最优退役路径如图 4(a)所示。由图 4(b)可知,该例中拆除人员的总剂量在迭代900次左右达到收敛,最优路径对应受照总剂量为6.135×10-10Gy。
|
图 4 单元数M=5时核设施退役拆除优化路径结果 (a) 最优路径图,(b) 遗传算法迭代曲线 Figure 4 Results of dismantling route optimization during nuclear decommissioning when the unit number M=5. (a) Optimal dismantling route, (b) Iteration of genetic algorithm |
由计算结果可知,最优路径可能存在于分多次拆除同一器件情况下。另外,针对核设施拆除过程中可能造成的二次污染,可通过剂量估算后,再次计算辐射场,利用功能软件进行二次寻优。
4 功能软件开发利用MATLAB实现了基于遗传算法求解旅行商问题下的最优退役路线,并通过GUI设计了面向核设施退役过程的辐射场重构与拆除路径优化功能软件。
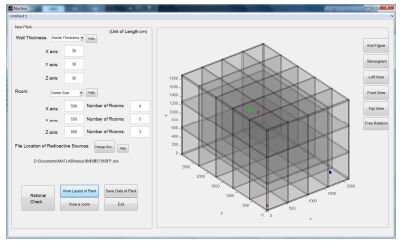
图 5为新建厂房数据界面,在该界面可进行三维情景设计,包括放射性器件数据如器件位置、形状、尺寸、活度、拆除所需时间及厂房相关数据并保存,厂房及任意房间的布局可视。
|
图 5 新建厂房数据界面 Figure 5 Interface of creating the plant data. |
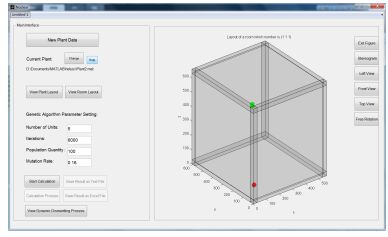
图 6为最优路径求解界面,可在该界面更换保存的厂房数据,调整器件单元数M、迭代次数、种群数量等参数,并显示遗传算法求解最优路径的进程,所得结果可保存为文本文件或Excel文件。
|
图 6 求解最优路径界面 Figure 6 Interface of calculating the optimal route. |
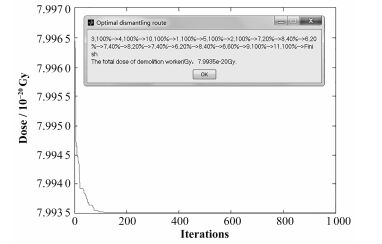
图 7为最终的结果,给出了迭代次数与拆除人员受到总剂量的曲线,可以得到收敛后所受的最小剂量值。图 7还给出了最优拆除路径,最优路径窗口中按最优路径依次显示了每次要拆除的器件以及所要拆除的百分比。
|
图 7 最终结果 Figure 7 The final results. |
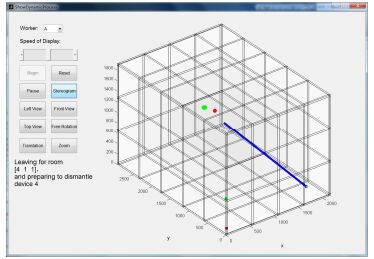
图 8为最优拆除路径的动态显示,显示速度可调。正被拆除的器件的颜色将不停变化,尺寸将不断变小。该界面以一条移动的短线显示拆除人员在器件间的运动过程。
|
图 8 最优路径的动态显示图 Figure 8 Dynamic view of optimal dismantling route. |
针对核设施退役过程中多源项的三维辐射场,发展了基于点核积分的辐射场快速重构方法,并利用蒙特卡罗程序验证。核退役拆除路径问题抽象为类TSP问题数学模型,构造不同拆除路径下所受外照射的剂量矩阵,根据辐射防护ALARA原则,利用遗传算法寻优计算。计算给出了多源项拆除实例最优化拆除路径和三维显示,并对优化效果进行了讨论。基于以上方法设计开发了面向核设施退役过程的辐射场重构与拆除路径优化功能软件。据此可进一步研究多旅行商问题下的核退役拆除路径优化问题,并考虑核设施退役过程中的个人受照剂量、集体受照剂量、经济代价、环境影响和公众心理等众多影响因素,实现核设施退役过程中的辐射防护最优化,为核设施退役提供更合理、有效的决策方案。
| [1] | Leservot A, Chodorge L. Chavir:a virtual site simulation environment[C]. European Nacigation Conference, Versailles, French, 2005. |
| [2] | Rodenas J, Zarza I, Burgos M C, et al. Developing a virtual reality application for training nuclear power plant operators:setting up a database containing dose rates in the refuelling plant[J]. Radiation Protection Dosimetry, 2004, 111(2): 173–180. DOI: 10.1093/rpd/nch043 |
| [3] | Kim Y H, Park W M. Use of simulation technology for prediction of radiation dose in nuclear power plant[M]. Springer Berlin Heidelberg: Computational and Information Science, 2004: 413-418. |
| [4] | Park H S, Kim G H, Lee K W, et al. Development of animation and simulation module for evaluation of Worker's dose[C]. Waste Management Symposium, Tucson, United States, 2007. |
| [5] |
戴波, 张永领, 周斌, 等. 反应堆退役仿真技术研究方案[J].
核动力工程, 2013, 34(3): 168–171.
DAI Bo, ZHANG Yongling, ZHOU Bin, et al. Study scheme of reactor decommissioning simulation technology[J]. Nuclear Power Engineering, 2013, 34(3): 168–171. |
| [6] |
杨子辉. 大规模辐射场景三维实时仿真关键技术研究[D]. 合肥: 中国科学技术大学, 2016.
YANG Zihui. Study on key technologies of three-dimensional real-time simulation for large-scale radiation scenario[D]. Hefei:University of Science and Technology of China, 2016. |
| [7] |
晁楠, 刘永阔, 李梦堃, 等. 核设施退役场景的仿真实现技术研究[J].
应用科技, 2015, 42(6): 62–66.
CHAO Nan, LIU Yongkuo, LI Mengkun, et al. A scene simulation system for decommissioning of nuclear facilities[J]. Applied Science and Technology, 2015, 42(6): 62–66. |
| [8] |
谢小龙, 胡国辉. 虚拟现实技术在核设施退役中的应用[J].
科技创新导报, 2013, 260(8): 93–94.
XIE Xiaolong, HU Guohui. Application of virtual reality technology in the decommissioning nuclear facilities[J]. Science and Technology Innovation Herald, 2013, 260(8): 93–94. |
| [9] |
吴宜灿, 何桃, 胡丽琴, 等. 核与辐射安全仿真系统SuperMC/RVIS2.3研发与应用[J].
原子能科学技术, 2015, 49(Suppl 1): 7–15.
WU Yican, HE Tao, HU Liqin, et al. Development of virtual reality-based simulation system for nuclear and radiation safety[J]. Atomic Energy Science and Technology, 2015, 49(Suppl 1): 7–15. DOI: 10.7538/yzk.2015.49.S0.0007 |
| [10] |
席福坤, 方邦城. 计算g射线点核积分的蒙特卡罗方法[J].
核动力工程, 1987, 8(2): 66–74.
XI Fukun, FANG Bangcheng. A Monte Carlo method of the point kernel integration for gamma rays calculation[J]. Nuclear Power Engineering, 1987, 8(2): 66–74. |
| [11] | Holland J H. Adaptation in natural and artificial systems[M]. Cambridge, Massachusetts: MIT Press, 2015. |
