电子能量损失谱学是一种重要的物质分析技术，它基于电子与样品的非弹性散射过程，通过测量不同能量损失的散射电子来获得物质的电子结构信息^[1-2]。电子能量损失谱学已被广泛用于原子分子的电子结构和碰撞动力学、固态材料表面物理化学性质、催化科学等领域的研究^{[1, 3]}。对于低能电子入射，一方面，无法获得高空间分辨的靶样品信息^[3]；另一方面，由于样品靶分子波函数会受到入射电子的影响而发生扭曲，不能得到纯粹的靶分子电子结构信息^[1]。因此，开展中高能区的电子能量损失谱学研究就非常有必要了，其关键之一在于研制一台产生中高能电子束的电子枪。之前的电子与原子分子碰撞研究小组的仪器主要集中于中低能区^[4-7]，中高能区仅有几个小组：加拿大Brion小组^[8]谱仪工作能量为3 keV和8 keV，对应的能量分辨为48meV和1 eV，缺点是不可转角度测量；日本Ohtani小组^[9]谱仪工作在中能区（500 eV和800 eV）；巴西Souza小组^[10]工作能量为1 keV，能量分辨为0.6eV。本课题组在自主研发的一台谱仪^[11]上（工作能量为1.5 keV和2.5 keV，能量分辨约为60 meV）开展了一系列的原子分子结构和动力学研究工作^[12-14]。本文研制了一种电子束能量大范围可调的中高能区电子枪，利用计算机模拟，优化了其电子光学性能，并进行了测试，获得了电子枪发射束流的流强、发散角和束斑等参数，与以前所用电子枪^[11]相比性能有了极大提升。

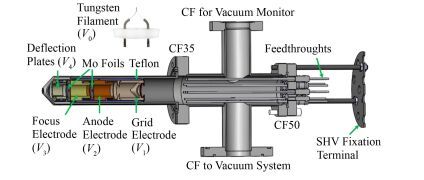
电子枪的作用为产生电子束并对其进行加速、聚焦和偏转，基本结构如图 1所示。主要由电子透镜系统和真空系统构成。电子透镜系统包括发叉型钨灯丝V₀、栅极V₁、阳极V₂、聚焦极V₃、偏转板V₄和钼片（中心有直径3 mm的膜孔）。灯丝通过压片固定在栅极上，其他电极之间通过聚四氟乙烯垫片进行绝缘隔离和机械定位，并由螺丝固定在无磁不锈钢套筒内。每个电极上都有电极引线，可连接到外面的高压电源。整个电子透镜系统固定在标准CF35法兰上，形成一个独立模块，可以方便连接于任何所需仪器设备上，且带有独立的真空抽气接口，可实现差分抽气，对所使用场合的真空环境要求较低。电子枪真空系统主要由用于连接分子泵抽真空和真空度监测的法兰构成。另外，电气贯穿引线焊接在CF50法兰上实现真空隔离，通过SHV高压头与电源相连。

图 1

图 1 电子枪结构 Figure 1 Structure of the electron gun

加电工作时（电子枪内真空度要求好于约10^-4Pa），特殊形状的栅极（图 1）可以控制灯丝热发射电子束的形状和流强。阳极电位高于栅极，可用于电子束的引出和聚焦^[15]。因此，通过调节栅极和阳极电位大小可以控制发射电子束流强。经过阳极一级聚焦的电子束，到达聚焦极后被二级聚焦至靶点处。调节偏转板所加电位可以实现电子束二维偏转。

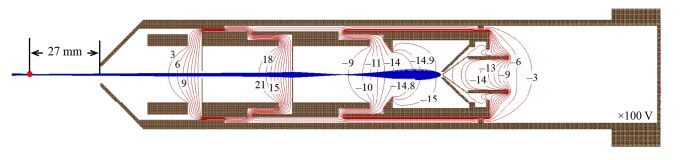
电子枪的主要电子光学设计指标为：1) 电子束能量在1-3 keV能区可调；2) 电子束流强约为5 μA（1500 eV能量下）；3) 样品处电子束径约为1 mm，发散角小于1°。为了实现上述目标，电子透镜系统采用二级聚焦圆桶透镜。为了在不同电子束能量下获得电子枪电极几何尺寸、电子光学性能的最优化，利用SIMION电子光学软件^[16]模拟了电子束的加速、聚焦和偏转过程。图 2为1500 eV能量下电子光学的模拟情况（图 2中曲线为电场等势线），电子束在距出口27 mm处，其束径为0.70 mm，发散角为0.90°。表 1给出了1-3 keV能区几个能量点的模拟结果，电子束径均小于1 mm，发散角均小于1°，且二者都随电子能量增加而逐渐减小，满足电子光学设计要求。束流强度指标的检验在§3给出。

图 2

图 2 电子能量为1500 eV下电子枪的电子光学模拟结果和等势线 Figure 2 Simulation of electronic optics for electron gun at an electron energy of 1500 eV and the equipotential lines of the electric field

表 1

表 1 不同电子能量下的电子光学模拟结果 Table 1 Simulated results of electronic optics at different electron energies 电子能量 Electron energy / eV 电位V1 V1 / V 电位V2 V2 / V 电位V3 V3 / V 发散角 Divergence angle / (°) 束斑直径 Diameter of beam spot / mm 1 000 ‒1 003 ‒590 1 700 0.99 0.81 1 500 ‒1 503 ‒885 2 600 0.90 0.70 1 500 ‒1 501.5 200 ‒1 080 0.89 0.54 2 000 ‒2 003 ‒1 180 3 466 0.69 0.63 2 500 ‒2 503 ‒1 475 4 334 0.58 0.54 3 000 -3 003 -1 700 5 200 0.45 0.39

表 1 不同电子能量下的电子光学模拟结果 Table 1 Simulated results of electronic optics at different electron energies

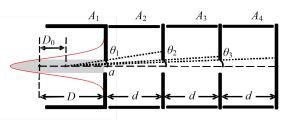
为了测试电子枪主要的性能指标，即电子束流强度、束斑尺寸和发散角，设计了如图 3所示的测试配件来测量相关物理量。它由一个不锈钢桶状基座A₁和三片相互平行排列的喷涂有胶体石墨的钼片（A₂、A₃和A₄）组成。碰撞靶点和基座A₁与电子枪出口相距分别为D₀=10 mm、D=27 mm。A₁、A₂、A₃和A₄之间相距d=30 mm，A₁、A₂和A₃中心有一孔径为2a=1 mm的膜孔。基座和钼片间通过三根绝缘杆支撑固定，钼片外接电极，用于电流检测。

图 3

图 3 测试配件示意图 Figure 3 Schematic diagram of the test accessory

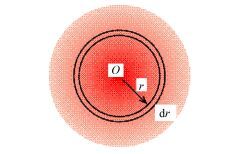
聚焦电子束在横截面上的电子密度分布满足高斯函数^[17]n(r)（图 3中曲线所示），如图 4所示，O点电子密度最大，随半径r增大而逐渐减小。根据电流定义，环带r→r+dr内的电流微元dI为：

图 4

图 4 电子束密度分布示意图 Figure 4 Schematic diagram of electron density distribution

式中：e为基本电荷电量；n₀为电子密度幅度参数；σ_r为高斯函数标准差（电子束径${\mathit{\Gamma } _r} = 2\sqrt {2\ln 2} {\sigma _r}$）。由于热电子能量分散0.5 eV远小于电子动能，例如1500 eV，可认为所有的电子速度近似相等，即υ_e。据此，半径r内的总电子束流强度I_c（即图 3中曲线下方阴影部分所含的电子）为：

为了得到电子束径Γ_r，可以通过调节电子枪偏转板电压来偏转电子束，使得束流最大可能地通过基座小孔，同时检测A₁、A₂、A₃和A₄上的电流，根据：

可以反推得σ_r，即得到A₁处的电子束径Γ_r。其中：η为电子束通过A₁膜孔的通过率；I_i(i=1, 2, 3, 4) 为相应部位A_i (i=1, 2, 3, 4) 上检测到的电流值；I为电子束总流强。

同理，假定电子束发散角分布也满足高斯函数，且近似认为电子在配件中沿着发散角方向直线飞行，因此可以获得在不同发散角度θ_j内（如图 3所示，可根据几何关系得到）的电子束所占比例：

式中：j=1, 2, 3；σ_θ为高斯函数标准差；参数$ {\Gamma _\theta } = \sqrt {2\ln 2} {\sigma _\theta }$为束流发散角。

测试时，电子枪灯丝电源被浮置在负主高压电源上，束流聚焦处为地电位。因此，主高压电源的电压值决定了电子束最终的能量。栅极的主要作用是控制电子束发射形状、强度和微聚焦，其电位要稍低于灯丝电位。实际操作中，也将栅极电源浮置在负主高压电源上。阳极电位远高于灯丝电位，与栅极一起构成一级聚焦。聚焦极与阳极一起作为主要的聚焦透镜，通过调节所加电位将电子束聚焦至靶点处。阳极和聚焦极都有电源单独供电。

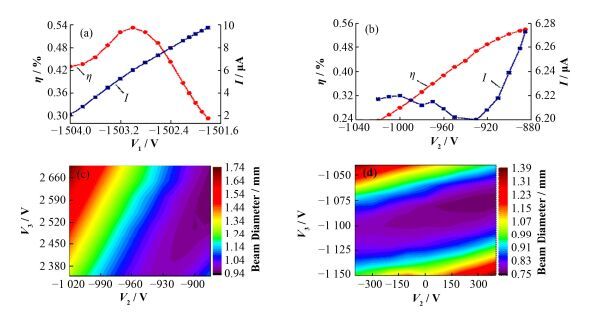
为了评估某个电极对束流聚焦特性和束流强度的影响，通过固定优化后的其他电极电压，改变该电极电压，测量电子束通过A₁膜孔的通过率η可以获得相关信息。以电子能量1500 eV为例，图 5(a)显示了随着栅极电位V₁减小 (V₂=-890 V，V₃= 2600V)，总束流强度I近似线性减小；通过率η先增大至最大值，再逐渐减小。图 5(b)为I、η与阳极电位V₂的变化关系 (V₁=-1503 V，V₃=2600 V)，随着V₂逐渐增大，I先逐渐减小至最小，再线性增大；η先近似线性增大，再缓慢增大至最大值。

图 5

图 5 电子能量为1500 eV下电子枪测试结果 Figure 5 Test results of electron gun at electron energy of 1500 eV

为了评估式 (3) 的聚焦束模型的正确性，对比了实验测量和SIMION模拟得到的束径Γ_r。加速模式下 (V₁=-1503 V，V₂=-885 V，V₃=2600 V)，测得η=53.93%，Γ_r=0.95 mm；模拟得到η=71.64%，Γ_r= 0.70mm（表 1），其相对偏差分别为32.84%和26.32%。相应地，减速模式下 (V₁=-1501.5 V，V₂= 200 V，V₃=-1080 V)，测得η=70.76%，Γ_r=0.75 mm；模拟得到η=78.89%，Γ_r=0.54 mm（表 1），其相对偏差分别为11.49%和28.00%。可见，测量值和模拟值之间存在一定差异，但其偏差在可接受范围内，这是因为：1) 电子束流强较大，SIMION模拟过程没有考虑空间电荷效应；2) 加速模式下，聚焦极V₃和偏转板V₄之间压差很大，引起电场分布发生畸变（偏转板处为正方形分布），进而导致电子束束斑的畸变。

由不同实验条件下测量得到的η，根据式 (3) 可以获得相应的电子束径大小。图 5(c)和(d)分别是加速和减速模式下测量得到的束径Γ_r随V₂和V₃变化的等高线图。加速模式下，Γ_r等高线呈斜带状分布，倾斜斜率k_a约为6.28，最小束径分布于V₂ > -970 V区域；减速模式下，Γ_r等高线也呈斜带状分布，倾斜斜率k_d约为0.04，远小于k_a，最小束径分布于V₃ > -1130 V区域。这意味着减速模式下，Γ_r在V₂和V₃构成的平面内具有更宽广、更稳定的最小束斑分布区间。

同时，通过测得的各钼片A_i上的电流I_i，根据式 (4) 可以获知电子束发散角的情况。例如，在1500eV电子能量下，测得减速模式 (V₁=-1501.5 V，V₂=200V，V₃=-1080 V) 下各电流值分别为：I₁= 0.696 μA，I₂=0.653 μA，I₃=0.459 μA，I₄=0.509 μA。据此，电子束发散角小于θ₁=1.68°的占ε₁=69.96%；发散角小于θ₂=0.61°的占ε₂=41.78%；发散角小于θ₃=0.37°的占ε₃=21.97%。利用式 (4) 拟合，可得σ_θ=0.79°、Γ_θ=0.93°，与模拟得到的束流发散角0.89°（表 1）符合得很好。因此，这一结果验证了电子束发散角分布满足高斯函数的模型，检测结果也显示满足所需指标。

本文研制了一台能量在1-3 keV可调的电子能量损失谱仪用中高能电子枪，并测试了电子枪发射束流的特性。为了获得最优的束流条件，利用SIMION电子光学软件模拟了电子发射源大小和初始发散角对靶点处的束斑大小和束流发散角的影响。在电子能量1.5 keV下，在离电子枪出口27 mm处可获得束径约0.95 mm、束流发散角约0.93°和束流强度6.27 mA的电子束，满足电子能量损失谱仪的使用要求。同时，电子枪测试和模拟结果吻合得较好，验证了聚束电子束电子密度和发散角分布的高斯函数模型。