为了进一步推动核能的技术发展，四代堆国际论坛提出了第四代核能系统概念，使其具有更好的安全性、经济竞争力、防核扩散性，以及更少的放射性核废物排放。第四代核能系统选出气冷快堆、铅冷快堆、熔盐堆、钠冷快堆、超临界水冷堆、超高温气冷堆6种候选堆型作为未来先进堆型的研发重点^[1]。在20世纪50-60年代，美国橡树岭国家实验室 (Oak Ridge National Laboratory, ORNL) 通过飞行器反应堆实验 (Aircraft Reactor Experiment, ARE) 和熔盐实验堆 (Molten Salt Reactor Experiment, MSRE) 项目研究过熔盐堆，其中ARE在1954年满功率运行40 h，MSRE在1965-1969年满功率运行475 d^[2-3]。

中国科学院上海应用物理研究所目前正在承担中国科学院战略性科技先导专项——钍基熔盐堆核能系统，部署了固态燃料熔盐堆 (Thorium Molten Salt Reactor-Solid Fuel, TMSR-SF) 和液态燃料熔盐堆 (Thorium Molten Salt Reactor-Liquid Fuel, TMSR-LF) 的研发。为充分利用中国丰富的钍资源，钍基熔盐堆采用²³²Th作为熔盐堆的可增殖核燃料，通过中子俘获增殖出易裂变燃料²³³U。钍基液态燃料熔盐堆作为四代堆中唯一的液态燃料核反应堆，由于在线燃料添加和在线处理（如中子毒物去除和重金属回收），可以实现较低的剩余反应性运行及较高的中子经济性。在线处理流程主要包括氦鼓泡法、氟化挥发法、电解法等。氦鼓泡法可以在线快速提取Xe、Kr等惰性气体和一些难溶的惰性金属；需要处理的熔盐先通过氟化挥发法提取分离U、Np、Pu等锕系核素，然后再利用电解还原提取分离Pa和镧系核素，然后将锕系核素返回堆芯，去掉镧系核素，从而可实现熔盐堆的闭式循环^[4]。

热中子吸收截面很大的¹³⁵Xe是热堆中首要考虑的中子毒物^[5]。钍基液态燃料熔盐堆设计为热中子谱，其液态燃料在一回路循环的同时，核燃料裂变产生的¹³⁵Xe也在一回路随着熔盐循环往复，通过氦鼓泡法可以将产生的¹³⁵Xe从堆芯中分离出来，从而减小¹³⁵Xe的毒性并提高堆芯中子经济性^[6-7]。

目前国际上大部分针对熔盐堆性能研究的工作都是假设¹³⁵Xe只存在堆芯熔盐中，并认为去除能力仅取决于在线处理周期和氙提取率，从而给出熔盐堆有效增殖因子^[8-9]。本文在参考MSRE氙毒分析的基础上，将其用在钍基液态燃料熔盐堆概念设计上，评估氙毒对堆芯有效增殖因子的影响^[10-11]。

为了评估¹³⁵Xe对TMSR-LF1反应性的影响，以一回路为研究对象，我们建立了在线处理鼓泡法中的氙毒模型。反应堆一回路见图 1，分为堆芯、左侧管道、右侧热交换器管道和上部的泵碗4个部分，包含熔盐、石墨和氦泡，熔盐按顺时针循环。

图 1

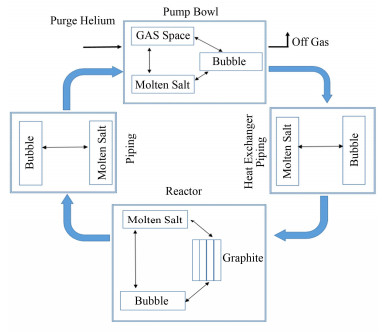
图 1 TMSR一回路熔盐流动示意图 Figure 1 TMSR molten salt flow in primary circuit.

采用氦气鼓泡法进行在线氙气去除，即从泵碗向熔盐充入氦气，氦气随熔盐在一回路流经热交换器、堆芯、管道，最终回到泵碗。其中氦气存在两种形式：一是溶解在熔盐中；二是在熔盐中以一定半径大小的氦泡存在。在一回路氦气向熔盐扩散和熔盐流动循环的过程中，氦气占熔盐的空泡比例达到平衡；同时，熔盐中产生的¹³⁵Xe扩散到氦泡被带出到泵碗中去除掉，从而减少氙毒对反应堆反应性的影响。氦气和¹³⁵Xe会在熔盐和氦泡之间扩散；同时熔盐中¹³⁵Xe会扩散到石墨，氦泡中¹³⁵Xe亦会通过碰撞传递到堆芯石墨。因此，¹³⁵Xe在熔盐、氦泡和石墨两两之间的互相传递是¹³⁵Xe其除燃耗和衰变外的主要行为。

熔盐中氙气向氦泡的扩散通量大小遵循菲克定律：

式中：J为扩散流量，与浓度差、质量传递系数h、氦泡和熔盐的接触面积A成正比；H为亨利系数；$C_{\rm{m}}^x$为熔盐中气体浓度；$C_{\rm{b}}^x$为氦泡中气体浓度；R为气体常数；T为反应堆温度。在一回路的4部分区域，上述扩散规律不仅适用于¹³⁵Xe在熔盐和氦泡之间的扩散，也适用于¹³⁵Xe在熔盐和石墨、载气体氦气在熔盐和氦泡之间的扩散。

首先，不考虑¹³⁵Xe的存在，只分析鼓泡法的覆盖气体（即氦气）在一回路的循环及其在熔盐中的扩散。在特定的压力和流动条件下，鼓入的氦气达到稳定状态后，得到一回路各部分熔盐中氦气浓度和氦泡在各部分所占的空泡比例。由于一回路中各区域气体扩散原理的类似性，现以堆芯为研究对象，来分析溶解于熔盐的氦气浓度和以氦泡存在的氦气占流体体积的空泡比例。堆芯熔盐中氦的浓度变化由三部分决定：第一部分是从上流熔盐流入的氦气，使堆芯熔盐的氦浓度增大；第二部分是从堆芯熔盐流出的氦气，使堆芯熔盐的氦浓度减小；第三部分是堆芯内氦气从熔盐向氦泡的扩散，使堆芯熔盐的氦浓度减小。对于堆芯部分，熔盐中氦浓度变化规律：

同理，堆芯内氦泡占熔盐体积的空泡比例变化也是同样的规律，主要由前面所述三部分决定。熔盐中氦泡的空泡比例随时间的变化规律：

式中：Z_c为堆芯内熔盐中氦的浓度；Z_u为流入堆芯的上流熔盐（即热交换器中的熔盐）中氦的浓度；ψ_u为氦气在上流熔盐中的空泡比例；V_c为堆芯中熔盐和氦泡的体积总和；F₁为一回路的流量；h_b为气体向氦泡的质量传递系数；ψ_in是向泵碗中充入的氦泡初始空泡比例；$Z_{\rm{c}}^{\rm{b}}$为堆芯中氦泡的氦浓度；$Z_{\rm{u}}^{\rm{b}}$为流入堆芯的氦泡的氦浓度。

通过在管道、热交换器管道和泵碗中分别建立上述类似的氦浓度和氦空泡比例变化的微分方程，联立后即可求得一回路中氦气空泡比例变化情况及平衡状态。

其次，在氦气空泡比例稳定分布的基础上，进一步分析堆芯内产生的¹³⁵Xe在一回路的扩散和循环流动等行为。包括¹³⁵Xe在熔盐和氦泡之间的扩散、熔盐和石墨之间的扩散、氦泡和石墨之间的碰撞扩散，以及通过熔盐和氦泡在管道、堆芯和热交换器管道之间的流动等。

¹³⁵Xe在堆芯内的产生有三种途径：第一是²³⁵U直接裂变产生，产额为0.3%；第二是裂变产生的¹³⁵I，经过衰变生成¹³⁵Xe，产额为6.1%；第三是裂变产生的¹³⁵I衰变产生激发态的¹³⁵Xe，再次退激发而生成¹³⁵Xe。

¹³⁵Xe在氦泡和石墨之间的传递是通过碰撞的形式实现的。氦泡在一回路循环过程中，流经堆芯石墨与石墨表面发生碰撞，从而将裂变气体¹³⁵Xe传递到石墨。此过程中的碰撞以一定概率发生，将会增加石墨中¹³⁵Xe的浓度。碰撞概率越大，则石墨中¹³⁵Xe的毒性浓度越大，其对堆芯产生的中子毒性也越大。

一回路4部分熔盐中产生的¹³⁵Xe不仅随熔盐循环流动，也会发生衰变和向熔盐中的氦泡扩散。当熔盐和氦泡流经堆芯时，¹³⁵Xe会传递向石墨，并与中子发生核反应。在循环流动的过程中，当泵碗中氦泡去除的¹³⁵Xe和熔盐中产生的¹³⁵Xe达到平衡后，一回路各部分熔盐中的¹³⁵Xe浓度和氦泡中的¹³⁵Xe浓度也达到平衡。

以堆芯熔盐中¹³⁵Xe浓度的变化为例，主要受9个因素的影响。其中前4个为¹³⁵Xe增加项，分别是从上流熔盐流入堆芯、¹³⁵I的衰变、¹³⁵Xe激发态的衰变、核裂变产生；后5个为¹³⁵Xe减少项，分别是随熔盐流出堆芯、衰变、燃耗、熔盐向堆芯内氦泡的扩散、熔盐向石墨的扩散。这时，¹³⁵Xe的浓度变化如式 (4)：

式中：X_c为堆芯熔盐中¹³⁵Xe的浓度；X_u为上流熔盐中¹³⁵Xe的浓度；K_x为¹³⁵I衰变成¹³⁵Xe所占的比例；λ_I为¹³⁵I的衰变常数；I为¹³⁵I的浓度；X^e和λ_e分别为¹³⁵Xe的激发态核素的浓度和衰变常数；P为反应堆功率；Y_x为单位功率裂变产生¹³⁵Xe的量；φ为中子通量；σ为¹³⁵Xe的反应截面；A_b为熔盐和氦泡的接触面积；h_g为¹³⁵Xe向石墨的质量传递系数；$X_{\rm{c}}^{\rm{g}}$为石墨中¹³⁵Xe的浓度。

以堆芯为研究对象，分别给出了流动过程中氦泡所占空泡比例变化和¹³⁵Xe的产生与消失的行为描述。同理，在整个一回路中，管道、热交换器和泵碗也可以建立类似的微分方程组，求解即可得流动扩散平衡后氦气和氙气在一回路的状态。左侧管道和热交换器中氦气和氙气的分析，主要考虑熔盐流动和氙向氦泡扩散；泵碗中氦气和氙气的分析，需考虑氦气的充入和氙气的去除，去除能力决定了一回路¹³⁵Xe平衡浓度。整个一回路在泵碗的¹³⁵Xe去除和产生达到一个动态平衡，从而可以对鼓泡法的¹³⁵Xe毒性和去除规律进行分析和评估。¹³⁵Xe通过氦泡去除到泵碗：

去除能力与需要净化的旁路熔盐中氦泡流量F_b和去除效率S_b成正比。

氙毒大小主要决定于¹³⁵Xe在堆芯中（包括熔盐和石墨）的平衡浓度，可以用¹³⁵Xe吸收的中子在²³⁵U吸收中子所占的比例进行表征^[10]。其表达式如下：

式中：P_Xe为氙毒性。分子上的三项分别是堆芯中熔盐、石墨和氦泡中单位时间和单位体积内¹³⁵Xe吸收的中子数。

TMSR-LF1是中国科学院上海应用物理研究所承担的设计功率为2 MW、专门用于研究钍燃料转换性能的液态燃料熔盐实验堆。其燃料熔盐采用氟盐LiF-BeF₂-ThF₄-UF₄，易裂变燃料为²³⁵U（富集度w=16.2%），具体参数如表 1所示。堆芯几何模型如图 2所示，由燃料熔盐、石墨、控制棒组成。石墨可以分成堆芯活性区、上、下反射层和侧反射层。燃料熔盐也有4部分熔盐区域，分别为：堆芯活性区、上、下腔室和外围熔盐。堆芯压力容器采用哈氏合金 (Hastelloy-N alloy) 材料。

表 1

表 1 TMSR-LF1的堆芯参数 Table 1 TMSR-LF1 reactor core parameters. 参数Parameter 数值Value 铀富集度Uranium enrichment / % 16.2 熔盐密度Salt density / g∙cm-1 2.18 功率Power / MW 2 堆熔盐总体积Salt volume / m3 0.538 熔盐成分Salt composition LiF-BeF2-ThF4-UF4(70.2%-26.8%-0.07%-2.93%) 堆本体直径/高度Reactor diameter/height / cm 195/251 堆芯活性区直径/高度Core diameter/height / cm 110/110 径向石墨反射层厚度Radial reflector / cm 40 轴向石墨反射层厚度Axial reflector / cm 40

表 1 TMSR-LF1的堆芯参数 Table 1 TMSR-LF1 reactor core parameters.

图 2

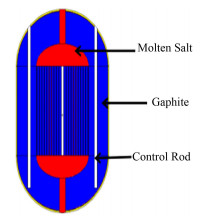
图 2 钍基熔盐液态堆 Figure 2 Schematic for TMSR-LF1.

由于熔盐和石墨对应的中子能谱不同，¹³⁵Xe吸收中子的反应率也不同，需分别考虑。TMSR-LF1的中子能谱由SCALE6.1给出（如图 3所示），各核素的微观截面来自ENDF/B-Ⅶ.1 (Evaluated Nuclear Date File)。SCALE软件是美国橡树岭开发的用于临界安全、堆物理、辐射安全和不确定度分析^[12]。软件经过了验证，是可靠的。世界各国的研究所都用其做反应堆的安全计算和设计^[13]。堆芯内的中子与各核素的反应率，在MATLAB平台上通过插值实现计算。

图 3

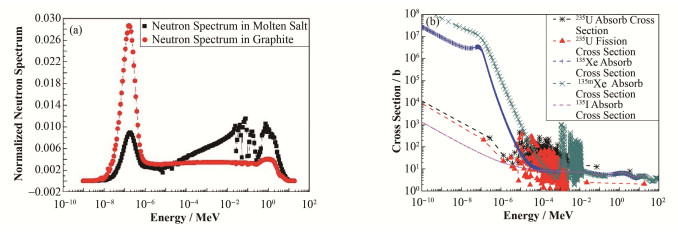
图 3 TMSR-LF1中熔盐、石墨的中子能谱 (a) 和模型所需核素的截面 (b) Figure 3 Neutron spectrum of molten salt and graphite (a) and cross section of nuclides (b).

TMSR-LF1一回路的流动参数、各部分体积大小和扩散系数是氦气和¹³⁵Xe平衡的重要参数（见表 2）；4个部分的体积由熔盐和氦泡组成的流体在一回路的体积共同决定。其中一回路流量决定了熔盐和¹³⁵Xe在一回路流动的快慢，净化的旁路流量决定了鼓泡法净化熔盐的快慢。¹³⁵Xe在熔盐和氦泡之间的扩散系数影响氦泡中¹³⁵Xe的浓度；熔盐和石墨之间的扩散系数影响石墨中¹³⁵Xe的浓度；此二者的相对大小决定了¹³⁵Xe在堆芯内熔盐、石墨和氦泡的扩散行为和相对浓度大小。

表 2

表 2 氙模型计算一回路参数 Table 2 Primary circuit parameters of the xenon model. 参数Parameter 数值Value 管道熔盐体积Molten salt volume in pipeline 5.01×105 cm3 泵碗熔盐体积Molten salt volume in pump 1.18×105 cm3 热交换器熔盐体积Molten salt volume in heat exchanger 1.06×106 cm3 堆芯熔盐体积Molten salt volume in core 5.15×105 cm3 一回路流量Primary circuit flux 20000 cm3∙s-1 净化旁路流量Bypass flow 1000 cm3∙s-1 熔盐和石墨间氙质量传递系数Xenon mass transfer coefficient between molten salt and graphite 1.8 cm∙h-1 熔盐和氦泡间氙质量传递系数Xenon mass transfer coefficient between molten salt and bubble 120 cm∙h-1 氦亨利系数Henry coefficient of helium 1.26×10-7 mol∙cm-3

表 2 氙模型计算一回路参数 Table 2 Primary circuit parameters of the xenon model.

基于上述气体产生、扩散、消失等规律描述公式，通过科学计算语言MATLAB^[14]建立了一回路鼓泡法去除氙气的模拟程序，将堆芯的核反应过程和一回路的流动扩散结合。其中用SCALE6.1计算中子输运过程的能谱和通量，并计算有效增殖因子^[15]。利用建立的模型计算得到了堆芯氙毒结果，并与MSRE的测量结果进行了对比，如图 4所示。由于MSRE的相关文献中没有明确给出氦泡和石墨的碰撞概率参数，在其他计算时用过0.9%的碰撞概率参数。在我们的理论模型计算中，采用了三个碰撞概率参数，分别为1.13%、0.87%和0.61%，得到的结果与MSRE模拟结果符合较好。此外，从图 4中可以看出，除了MSRE的第二个实验点，其他实验数据都与两种理论结果符合较好。因此可以证明我们新建的¹³⁵Xe毒模型计算的正确性，可以将其应用于TMSR-LF1的氙毒分析，评估堆芯性能。

图 4

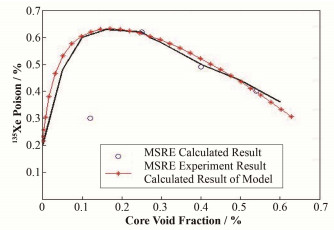
图 4 建立的模型计算结果和MSRE理论及实验测量的对比 Figure 4 Comparison of result from the newly developed code with the simulation and experiment data for MSRE.

由于氦气是去除氙气的载体，因此鼓泡法模拟时需先分析氦气的动态平衡，得出其平衡后氦泡的空泡比例。空泡比例越大，则¹³⁵Xe扩散到氦泡中越多，从而影响氙毒比例。在此基础上，进而分析¹³⁵Xe的扩散及其在一回路的流动。图 5给出了TMSR-LF1回路平衡后的氦泡在熔盐中的空泡比例 (Loop void fraction) 和初始充入回路的空泡比例 (Ingested void fraction) 的关系。由于向熔盐的扩散和压力的变化，平衡后的回路各部分的空泡比例总是小于从泵碗中初始充入的空泡比例。

图 5

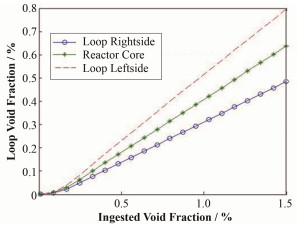
图 5 回路中平衡后氦泡的空泡比例 Figure 5 Helium bubble void fraction in the loop at balance.

¹³⁵Xe在一回路4部分都有特定的浓度分布，其中堆芯内的¹³⁵Xe影响中子经济性，堆芯中熔盐、氦泡和石墨中的¹³⁵Xe的浓度决定了氙毒的大小。

氦泡在堆芯内的空泡比例达到平衡，在此平衡状态下，¹³⁵Xe浓度分别在熔盐、氦泡和石墨中达到平衡。当达到平衡时，随着堆芯中氦泡空泡比例的增大，堆芯中总氙毒、石墨和熔盐中氙毒减小，氦泡中的氙毒增大；为更进一步理解鼓泡法对氙毒的影响规律，将此过程分解为三种情况。如图 6所示，横坐标表示堆芯氦泡的空泡比例，当空泡比例为零时表示没有氦泡存在，即没有鼓泡法；随着空泡比例增大，则堆芯中氦泡的数量增大，鼓泡法去除氦泡中氙的能力增强。第一种情况，只考虑¹³⁵Xe在熔盐和氦泡之间的扩散；第二种情况，考虑¹³⁵Xe在熔盐和氦泡、熔盐和石墨两种扩散；第三种情况，考虑¹³⁵Xe在熔盐和氦泡之间扩散、熔盐和石墨之间扩散以及氦泡和石墨碰撞（碰撞概率为0.4%）三种扩散，是鼓泡法中考虑¹³⁵Xe行为最全面的。上述三种情况中的鼓泡法去除率均为50%，图 6给出了三种情况下堆芯内总氙毒的对比。如前所述，目前国际上讨论熔盐堆鼓泡法¹³⁵Xe去除的效率时，都是认为¹³⁵Xe只存在熔盐中，直接从熔盐中去除，忽视了鼓泡法去除¹³⁵Xe的复杂性，不符合实际情况。通过上述情况的分析对比可知，必须在第三种情况的基础上对氙毒给出合理的描述，进而为在线¹³⁵Xe的去除给出合理的优化和建议。

图 6

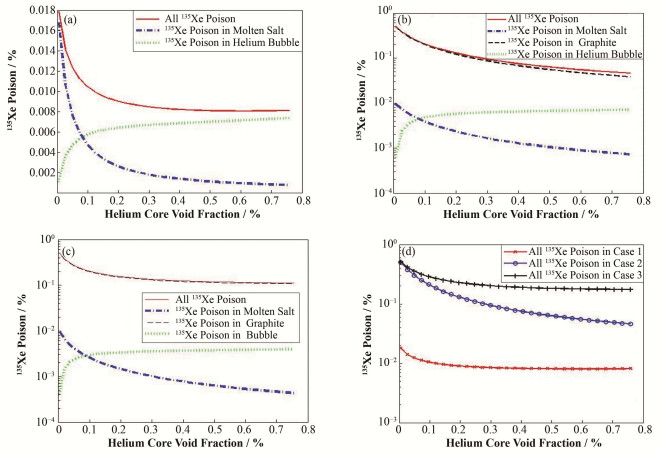
图 6 在Case 1 (a)、Case 2 (b)、Case 3 (c) 下的氙毒规律和三种情况下总的氙毒的对比 (d) Figure 6 135Xe poison regular at Case 1 (a), Case 2 (b), Case 3 (c) and the contrast of all poison (d).

对于上述三种情况，在鼓泡法50%去除效率下，氦泡在熔盐堆堆芯的比例越大，¹³⁵Xe去除能力越强，堆芯中的¹³⁵Xe毒性也随之减小。第一种情况与第二种情况的对比表明，不考虑¹³⁵Xe向石墨的扩散，即忽略了堆芯内石墨沉积的大量氙（明显高于熔盐和氦泡中的氙浓度，见图 6），计算的¹³⁵Xe毒性偏小。因此，如果在线处理鼓泡法模拟不考虑石墨中的氙沉积，将会严重高估堆芯反应性。第三种情况在第二种情况的基础上考虑了氦泡和石墨的相互作用，即流经石墨的熔盐中所含氦泡以一定概率与石墨碰撞，进一步增大了总毒性以及石墨中¹³⁵Xe毒性在总毒性中的比例；当碰撞概率为零时即为第二种情况。因此，减小氦泡和石墨的碰撞概率，同时增大鼓泡法的去除效率，可以有效减小¹³⁵Xe毒性。

图 7给出了TMSR-LF1不同去除效率下的氙毒及其对有效增殖因子的影响。从图 7(b)可以看出，在一定的氦气空泡比例情况下，氦泡的去除效率增大，平衡后堆芯总氙毒越小。图 7(a)选择了一个碰撞概率0.6%、去除效率100%的情形作为TMSR-LF1的氙毒去除的合理方案，并给出了有效增殖因子的变化。可以看出，没有鼓泡时（即横坐标氦泡在堆芯的空泡比例为零）时毒性最大；有鼓泡（即横坐标氦泡在堆芯的空泡比例大于零）时，氦泡空泡比例增大，可有效减小氙毒的影响。相对于没有鼓泡法，当考虑鼓泡法且氦气空泡比例达到0.6%时，可将TMSR-LF1的初始有效增殖因子提高1×10^-2。

图 7

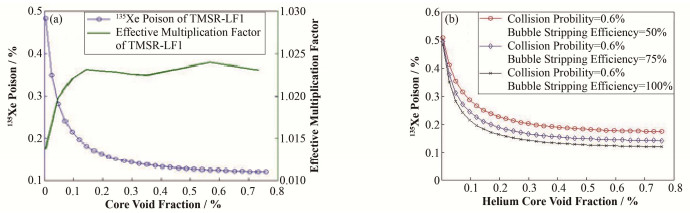
图 7 氦泡的去除效率对毒性的影响 (a) 和合理方案下不同氙毒对应的TMSR-LF1有效增殖因子的变化 (b) Figure 7 The influence of removal rate (a) and effective multiplication factor (b) at reasonable scheme.

本文利用MATLAB编程实现了熔盐堆鼓泡法去除¹³⁵Xe模型计算，在与MSRE理论计算及实验结果基础上，将此模型应用于中国科学院上海应用物理研究所设计的钍基液态熔盐实验堆上。以一回路为研究对象，以递进方式考虑了复杂的鼓泡法去除氙毒的分析，研究了鼓泡法去除效率对氙毒和有效增殖因子的影响，针对目前国际上熔盐堆鼓泡法理论模拟的不足，并给出了切合实际的鼓泡法氙毒分析模型。在综合考虑熔盐、石墨和氦泡三者之间¹³⁵Xe的扩散及氦泡与石墨的碰撞作用的基础上，给出了去除效率对氙毒的影响。研究结果表明，¹³⁵Xe向石墨的扩散是堆芯内氙毒增大的主要原因；提出了减小石墨中氙毒并提高去除效率的符合实际的最优方案，给出了对应的堆芯有效增殖因子的大小。在合理情况下，鼓泡法可以有效减小氙毒的影响，提高初始有效增殖因子。