2. 中国科学技术大学 合肥 230027
2. University of Science and Technology of China, Hefei 230027, China
靶核的热运动引起的多普勒效应会导致反应截面随温度发生变化,直接影响中子输运计算的结果。由于反应堆在实际运行过程中,堆内温度不断变化且变化范围广,为了准确模拟反应堆内中子与材料的相互作用,需要事先制作并存储大量不同温度点的核截面数据[1],导致粒子输运计算时内存占用极大。为此,蒙特卡罗输运程序常采用在线 (On-the-fly) 核截面生成方法获得所需温度的核截面数据,即在输运模拟中根据核素温度直接计算中子的反应截面,避免了直接存储大量核截面数据,减少了内存占用。由于在线核截面生成方法需实时计算中子各温度的反应截面,对方法的效率要求较高。
目前常用的在线多温度核截面生成方法主要有在线拟合方法[2]、靶核运动抽样方法[3]、近似多极点方法[4]及SIGMA1方法[5]。其中SIGMA1方法生成的核截面精度较高,且占用内存少[6-7]。该方法使用解析积分形式求解多普勒展宽方程,可将某一温度截面精确展宽至目标温度。但由于该方法中使用误差函数及泰勒级数展开方法,导致核截面的在线生成效率偏低。Dean等[8-9]对SIGMA1方法进行了优化,提出在共振峰较密集能区使用高斯-厄米特 (Gauss-Hermite) 积分,提高了多普勒展宽共振区域的核截面在线生成效率,但低能区域仍使用SIGMA1方法,综合计算效率仍较低。
本文基于超级蒙特卡罗核模拟软件系统SuperMC开展了基于分段高斯积分的在线多温度核截面生成方法研究,在多普勒展宽共振区域使用高斯-厄米特积分的基础上,提出在低能区域使用高斯-勒让德 (Gauss-Legendre) 积分,提高在线展宽的综合计算效率。SuperMC是一套通用、智能、精准的核设计与安全评价软件[10-13],已在聚变堆[14-16]、聚变裂变混合堆[17-18]以及铅冷快堆[19-21]等先进核能系统中得到了广泛的使用。
1 SIGMA1多温度核截面生成方法在自由气体模型假设下,一般认为靶核热运动速度满足麦克斯韦-玻尔兹曼 (Maxwell-Boltzmann) 分布,当前温度T2的有效核反应截面可由原始温度T1的核截面遵循以下形式推导得出:
| $ \begin{array}{c} {v^2}{\sigma _{{T_2}}}\left( v \right) = \sqrt {\frac{\beta }{{\rm{\pi }}}} \int_0^\infty {{{v'}^2}{\sigma _{{T_1}}}\left( {v'} \right)} \\ \;\;[{{\rm{e}}^{ - \beta {{\left( {v' - v} \right)}^2}}} - {{\rm{e}}^{ - \beta {{\left( {v' + v} \right)}^2}}}]{\rm{d}}v' \end{array} $ | (1) |
式中:T1、T2为热力学温度; ν为入射中子速度; ν'为中子与靶核的相对速率;σT(ν) 代表温度T时中子速度为ν的截面;β=M /[2k(T2-T1)],M为靶核质量,k为玻尔兹曼常数。
引入无量纲变量x2=βν′2,y2=βν2,简化式 (1) 得:
| $\begin{array}{c} {\sigma _{{T_2}}}\left( y \right) = \frac{1}{{{y^2}}}\sqrt {\frac{1}{{\rm{\pi }}}} \int_0^\infty {{x^2}{\sigma _{{T_1}}}\left( x \right)\left[ {{{\rm{e}}^{ - {{\left( {x - y} \right)}^2}}} - {{\rm{e}}^{ - {{\left( {x + y} \right)}^2}}}} \right]{\rm{d}}x} \\ = \sigma _{{T_2}}^*\left( y \right) - \sigma _{{T_2}}^*\left( { - y} \right) \end{array}$ | (2) |
其中:
| $ {\rm{\sigma }}_{{T_2}}^*\left( y \right) = \frac{1}{{{y^2}}}\sqrt {\frac{1}{{\rm{\pi }}}} \int_0^\infty {{x^2}{\sigma _{{T_1}}}\left( x \right){{\rm{e}}^{ - {{\left( {x - y} \right)}^2}}}{\rm{d}}x} $ | (3) |
由于式 (2) 中指数项的存在,
SIGMA1方法采用解析积分形式计算式 (2) 的积分值。为保证计算精度,需使用误差函数及泰勒级数展开方法,导致此方法效率较低。
2 基于分段高斯积分的多温度核截面生成方法本文在保证精度要求的前提下(与SIGMA1方法生成截面的相对偏差小于0.1%),针对SIGMA1方法效率问题,根据其不同能量区间多温度截面的特征,发展了基于分段高斯积分的在线多温度核截面生成方法。在多普勒展宽共振峰较密集区域使用高斯-厄米特积分方法,在低能区域使用高斯-勒让德积分方法。在保证核截面精度的同时提高了截面生成效率。
2.1 高斯-厄米特积分方法对于指定积分项
| $\int_{ - \infty }^\infty {f(z){{\rm{e}}^{ - {z^2}}}{\rm{d}}z} = \mathop \sum \limits_{k = 1}^n {w_k}f({z_k})$ | (4) |
其中:zk为厄米特多项式Hn的节点,定义如下:
| ${H_n}({z_k}) = {( - 1)^n}{{\rm{e}}^{{z^2}}}\frac{{{{\rm{d}}^n}}}{{{\rm{d}}{z_k}^n}}{{\rm{e}}^{ - {z_k}^2}}$ | (5) |
权重wk定义为:
| ${w_k} = \frac{{{2^{n - 1}}n!\sqrt {\rm{\pi }} }}{{{n^2}{{\left[ {{H_{n - 1}}({z_k})} \right]}^2}}}$ | (6) |
令式 (3) 中z=x-y,则式 (3) 可表示为:
| $\sigma _{{T_2}}^*(y) = \frac{1}{{{y^2}\sqrt {\rm{\pi }} }}\int_{ - y}^\infty {{{(z + y)}^2}{\sigma _{{T_1}}}(z + y){{\rm{e}}^{ - {z^2}}}{\rm{d}}z} $ | (7) |
式 (7) 还可分解为:
| $ \begin{array}{c} \sigma _{{T_2}}^*\left( y \right) = \frac{1}{{{y^2}\sqrt {\rm{\pi }} }}[\int_{ - \infty }^\infty {{{(z + y)}^2}{\sigma _{{T_1}}}\left( {z + y} \right){{\rm{e}}^{ - {z^2}}}{\rm{d}}z} - \\ _{}\int_{ - \infty }^{ - y} {{{(z + y)}^2}{\sigma _{{T_1}}}\left( {z + y} \right){{\rm{e}}^{ - {z^2}}}{\rm{d}}z} ] \end{array} $ | (8) |
由于z的范围为-4≤z < 4[5],故当y > 4时即可保证式 (8) 中第二项求积结果近似为0。此时式 (4) 中的高斯-厄米特积分公式可直接用于式 (8)。同时,考虑到y > 4时式 (2) 中的
| ${\sigma _{{T_2}}}\left( y \right) = \frac{1}{{{y^2}\sqrt {\rm{\pi }} }}\mathop \sum \limits_k^N f\left( {{z_k}} \right){w_k}$ | (9) |
式中:
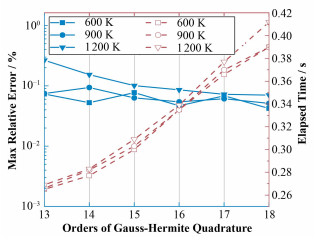
高斯-厄米特积分中积分节点的选取会对计算结果的正确性与计算效率产生影响。图 1中以典型核素238U为例,给出了不同的积分节点的高斯-厄米特积分方法与SIGMA1方法生成的核截面的最大相对偏差,并给出了高斯-厄米特方法的截面生成时间。从图 1可以看出,节点越多,计算结果越精确,但效率越低。当节点N≥16时,即可保证相对偏差ε < 0.1%。由于在线截面生成效率随节点数目增加而降低,为保证效率,多普勒展宽共振峰较密集区域 (E > 16kT/A) 选取16节点的高斯-厄米特积分方法。
|
图 1 不同高斯-厄米特积分节点生成截面的最大相对偏差及截面生成时间 Figure 1 Max relative error and broadening time with different Gauss-Hermite quadrature orders. |
当y≤4 (E≤16kT/A) 时,一般认为式 (2) 中的
| $\int_a^b {f\left( x \right){\rm{d}}x} \approx \frac{{b - a}}{2}\mathop \sum \limits_{k = 1}^n {\omega _k}f\left( {\frac{{b - a}}{2}{x_k} + \frac{{b + a}}{2}} \right)$ | (10) |
此时式 (2) 可表示为:
| ${\sigma _{{T_2}}}(y) = \frac{1}{{{y^2}}}\sqrt {\frac{1}{{\rm{\pi }}}} \mathop \sum \limits_i \frac{{{x_{i + 1}} - {x_i}}}{2}\mathop \sum \limits_{k = 1}^N {w_k}f(\frac{{{x_{i + 1}} - {x_i}}}{2}{x_k} + \frac{{{x_{i + 1}} - {x_i}}}{2})$ | (11) |
式中:
| ${P_n}\left( x \right) = \frac{{n!}}{{\left( {2n} \right)!}}\frac{{{{\rm{d}}^n}}}{{{\rm{d}}{x^n}}}{\left( {{x^2} - 1} \right)^n}$ | (12) |
wk定义为:
| ${w_k} = \frac{{2\left( {1 - {x^2}} \right)}}{{n\left[ {{P_{n - 1}}{{\left( x \right)}^2}} \right]}}$ | (13) |
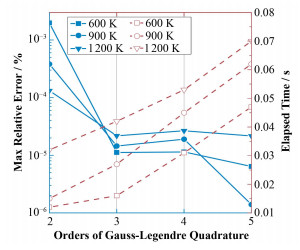
高斯-勒让德积分中积分节点的选取也会对计算结果的正确性与计算效率产生影响。同样以典型核素238U为例,分析不同积分节点对高斯-勒让德积分方法结果的正确性与计算效率的影响。图 2给出了高斯-勒让德积分方法与SIGMA1方法生成的核截面数据的最大相对偏差,以及高斯-勒让德方法的截面生成时间。从图 2可以看出,当节点N≥2时,高斯-勒让德积分方法最大相对偏差ε < 0.01%。由于在线截面生成效率随节点数目增加而降低,为保证效率,低能区域 (E≤16kT/A) 选取两节点的高斯-勒让德积分方法。
|
图 2 不同高斯-勒让德积分节点生成截面的最大相对 Figure 2 Max relative error and broadening time with different Gauss-Legendre quadrature orders. |
本文通过典型核素多温度截面在线生成测试及基准例题测试,从核截面数据本身和输运计算结果两方面验证本文方法的正确性及效率。
3.1 典型核素多温度截面在线生成测试本文基于典型核素 (16O、56Fe、90Zr、232Th、234U、235U、238U及239Pu) 300 K温度时的总截面,在线生成了600 K、900 K、1200 K温度时的总截面。
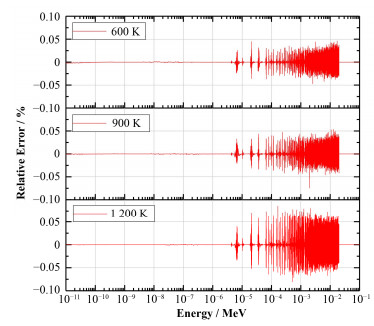
图 3给出了使用本文方法与SIGMA1方法生成的238U总截面的相对偏差。从图 3可以看出,当能量升高至共振能区时,受计算精度影响,两种方法的相对偏差随着温度升高逐渐增大,但在可分辨共振区范围内 (E < 0.02 MeV) 始终在0.1%以内。由于不可分辨共振能区的反应截面无法通过准确计算公式得到,在连续能量核数据库中以概率表方式存储。与SIGMA1处理方法类似,本文直接复制该能区的概率表信息。由图 3可见,当E≥0.02 MeV时,本文方法与SIGMA1方法的误差为0。
|
图 3 不同温度下本文方法与SIGMA1方法生成238U总截面的相对偏差 Figure 3 Relative error of 238U total cross sections between the proposed method and SIGMA1 method at different temperatures. |
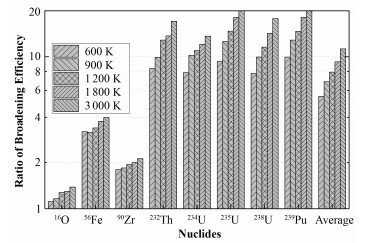
图 4给出了使用本文方法与SIGMA1方法在线生成各种温度下典型核素总截面的计算效率比,文中计算效率比是指相同温度下分别使用本文方法与SIGMA1方法展宽对指定核素在相同能量框架内展宽效率之比,与展宽时间比呈倒数关系。
|
图 4 本文方法与SIGMA1方法生成典型核素截面的展宽效率比 Figure 4 Ratio of broadening efficiency between the proposed method and SIGMA1 method for typical nuclides' cross section. |
从图 4可以看出,本文方法的计算效率与SIGMA1方法相比,轻核的在线截面生成效率提高约1.3倍,而重核的在线截面生成效率提高10倍以上,平均效率提高5倍以上。这是由于轻核(图 4中16O)截面出现的共振峰较少,能量框架较为稀疏,此时SIGMA1方法无需过多使用泰勒级数展开便可得到展宽结果。因此本文方法与SIGMA1方法效率较为接近,约1.3倍。对于共振核素(如图 4中238U及239Pu),因其截面出现的共振峰较多,SIGMA1方法为保证精度需频繁调用泰勒级数展开,导致其效率下降,而本文方法只需计算不同节点的求积函数即可完成截面处理,因此加速效果可高达20倍。从图 4中还可以看出,展宽所需目标温度越高,加速效果越明显。
3.2 基准例题测试为了进一步验证本文的方法,基于本文方法生成的截面进行了大量的输运计算基准例题的测试。本文给出Godiva及反应性多普勒系数基准例题的验证结果。
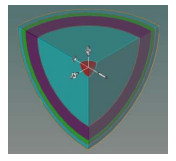
3.2.1 Godiva基准例题测试Godiva模型[22]为一个金属铀燃料球形裸堆,如图 5所示,燃料成分为235U、238U及234U。
|
图 5 Godiva模型1/8剖面图 Figure 5 1/8 section of Godiva model. |
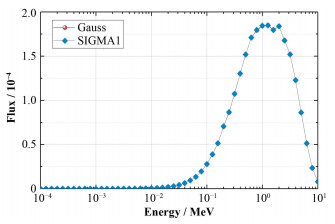
测试中使用原始温度为300 K的截面,分别由本文方法及SIGMA1方法在线展宽至600 K,计算Godiva模型的有效增殖因子及中子能谱。其中每代计算粒子数为20000,循环500代并舍去前50个非活跃代。本文方法有效增殖因子计算结果为0.99996±0.00019,SIGMA1方法有效增殖因子计算结果为0.99993±0.00019,能谱计算结果见图 6。
|
图 6 Godiva能谱对比 Figure 6 Energy spectra comparison of Godiva. |
从图 6结果可以得出,本文方法与SIGMA1方法所产生的截面计算得到的有效增殖因子相对偏差仅为0.003%;能谱的最大偏差小于0.5%。
3.2.2 反应性多普勒系数基准模型测试反应性多普勒系数基准模型旨在验证反应性多普勒系数计算结果的正确性,要求计算结果与基准值的相对偏差不超过10%[23]。该基准模型为一个简单的栅元结构,燃料为UO2,慢化剂为轻水,包壳材料为天然锆。栅元轴向无限长,慢化剂外表面使用反射边界条件。慢化剂的温度固定为600 K,燃料区的温度包含600 K和900 K,分别代表热态零功率 (Hot Zero Power, HZP) 和热态满功率 (Hot Full Power, HFP) 两个运行状态。该基准模型中通过分别计算燃料温度为600 K和900 K时的有效增殖因子,得到温度引起的反应性多普勒系数Dc,其表达形式如下:
| ${D_{\rm{c}}} = \frac{{\Delta {\rho _{{\rm{Dop}}}}}}{{\Delta {T_{{\rm{Fuel}}}}}}$ | (14) |
式中:ΔρDop=(kHFP-kHZP)/( kHFP×kHZP);ΔTFuel=300 K。
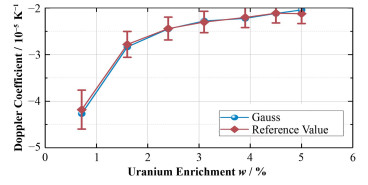
本文使用原始温度为300 K的核截面,在线展宽得到600 K和900 K的核截面,计算Dc。每代计算粒子数为20000,循环500代并舍去前50个非活跃代。Dc的计算结果如图 7所示。
|
图 7 反应性多普勒系数计算结果 Figure 7 Results of Doppler defect coefficients. |
使用本文方法计算得到的不同富集度下Dc均在基准值误差范围内,且与基准值的最大相对偏差为3.77%,低于基准模型中要求的10%,表明计算结果满足基准模型的精度要求。
4 结语本文发展了基于分段高斯积分的在线多温度截面生成方法,在多普勒展宽共振峰较密集区域使用高斯-厄米特积分方法,在低能区域使用高斯-勒让德积分方法。为了验证本文发展的方法,进行了典型核素截面的对比以及Godiva与多普勒反应性系数基准例题的测试。计算结果表明,本文方法能够快速并准确地生成各种温度下的中子截面,在保证精度的前提下,典型核素的在线生成效率平均提高了5倍以上,某些核素如238U和239Pu提速高达20倍,验证了本文方法的正确性以及高效性,可用于反应堆多物理耦合计算。
致谢 本文开展研究工作中得到了FDS团队其他成员的大力帮助和支持,在此深表感谢!| [1] | Trumbull T. Treatment of nuclear data for transport problems containing detailed temperature distribution[R]. Niskayuna, NY: Knolls Atomic Power Laboratory (KAPL), 2006. |
| [2] | Yesilyurt G, Martin W, Brown F. On-the-fly Doppler broadening for Monte Carlo codes[J]. Nuclear Science and Engineering, 2012, 171(3): 239–257. DOI: 10.13182/NSE11-67 |
| [3] | Viitanen T, Leppanen J. Explicit treatment of thermal motion in continuous-energy Monte Carlo tracking routines[J]. Nuclear Science and Engineering, 2012, 171(2): 165–173. DOI: 10.13182/NSE11-36 |
| [4] | Forget B, Xu S, Smith K. Direct Doppler broadening in Monte Carlo simulations using the multipole representation[J]. Annals of Nuclear Energy, 2014, 64: 78–85. DOI: 10.1016/j.anucene.2013.09.043 |
| [5] | Cullen D. Exact Doppler-broadening of tabulated cross section[J]. Nuclear Science and Engineering, 1976, 60(3): 199–229. DOI: 10.13182/NSE76-1 |
| [6] | Macfarlane R. The NJOY nuclear data processing system[R]. LA-UR-12-27079, Los Alamos National Laboratory, 2012. |
| [7] | Cullen D. PREPRO 2015-2015 ENDF/B pre-processing codes[R]. IAEA-NDS-39, International Atomic Energy Agency, 2015. |
| [8] | Dean C, Perry R, Neal R, et al. Validation of run-time Doppler broadening in MONK with JEFF3.1[C]. International Conference on Nuclear Data for Science and Technology, Jeju Island, South Korea, 2010. |
| [9] | Romano P, Trumbull T. Comparison of algorithm for Doppler broadening pointwise tabulated cross sections[J]. Annals of Nuclear Energy, 2015, 75: 358–364. DOI: 10.1016/j.anucene.2014.08.046 |
| [10] | Wu Y C, Song J, Zheng H Q, et al. CAD-based Monte Carlo program for integrated simulation of nuclear system SuperMC[J]. Annals of Nuclear Energy, 2015, 82: 161–168. DOI: 10.1016/j.anucene.2014.08.058 |
| [11] |
吴宜灿, 胡丽琴, 罗月童, 等. 先进核能系统设计分析软件与数据库研发进展[J].
核科学与工程, 2010, 30(1): 55–64.
WU Yican, HU Liqin, LUO Yuetong, et al. Development of design and analysis software for advanced nuclear systems[J]. Chinese Journal of Nuclear Science and Engineering, 2010, 30(1): 55–64. |
| [12] |
吴宜灿, 宋婧, 胡丽琴, 等. 超级蒙特卡罗核计算仿真软件系统SuperMC[J].
核科学与工程, 2016, 36(1): 62–71.
WU Yican, SONG Jing, HU Liqin, et al. Super Monte Carlo simulation program for nuclear and radiation process SuperMC[J]. Chinese Journal of Nuclear Science and Engineering, 2016, 36(1): 62–71. |
| [13] | Wu Y C, Xie Z S, Fischer U. A discrete ordinates nodal method for one-dimensional neutron transport calculation in curvilinear geometries[J]. Nuclear Science and Engineering, 1999, 133(3): 350–357. |
| [14] | Wu Y C, FDS Team. Conceptual design and testing strategy of a dual functional lithium-lead test blanket module in ITER and EAST[J]. Nuclear Fusion, 2007, 47(11): 1533–1539. DOI: 10.1088/0029-5515/47/11/015 |
| [15] | Wu Y C, FDS Team. Design analysis of the China dual-functional lithium lead (DFLL) test blanket module in ITER[J]. Fusion Engineering and Design, 2007, 82: 1893–1903. DOI: 10.1016/j.fusengdes.2007.08.012 |
| [16] | Wu Y C, FDS Team. Conceptual design of the China fusion power plant FDS-Ⅱ[J]. Fusion Engineering and Design, 2008, 83: 1683–1689. DOI: 10.1016/j.fusengdes.2008.06.048 |
| [17] | Wu Y C, Jiang J Q, Wang M H, et al. A fusion-driven subcritical system concept based on viable technologies[J]. Nuclear Fusion, 2011, 51(10): 103036. DOI: 10.1088/0029-5515/51/10/103036 |
| [18] | Wu Y C, Zheng S, Zhu X, et al. Conceptual design of the fusion-driven subcritical system FDS-Ⅰ[J]. Fusion Engineering and Design B, 2006, 81: 1305–1311. DOI: 10.1016/j.fusengdes.2005.10.015 |
| [19] | Wang M H, Huang H, Lian C, et al. Conceptual design of lead cooled reactor for hydrogen production[J]. International Journal of Hydrogen Energy, 2015, 40: 15127–15131. DOI: 10.1016/j.ijhydene.2015.04.009 |
| [20] | Huang Q Y, Li J, Chen Y. Study of irradiation effects in China low activation martensitic steel CLAM[J]. Journal of Nuclear Materials, 2004, 329-333: 268–272. DOI: 10.1016/j.jnucmat.2004.04.056 |
| [21] | Huang Q Y, Gao S, Zhu Z Q, et al. Progress in compatibility experiments on lithium-lead with candidate structural materials for fusion in China[J]. Fusion Engineering and Design, 2009, 84: 242–246. DOI: 10.1016/j.fusengdes.2008.12.038 |
| [22] | Briggs J, Michael A, Yolanda R. International handbook of evaluated criticality safety benchmark experiments[R]. NEA/NSC/DOC (95)03, Nuclear Energy Agency, 2006. |
| [23] | Mosteller R. ENDF/B-V, ENDF/B-VI, ENDF/B-Ⅶ.0 results for the Doppler-defect benchmark[R]. LA-UR-07-0922, Los Alamos National Laboratory, 2007. |


