2. 中国科学院近代物理研究所 兰州 730000;
3. 中国科学院大学 北京 100049
2. Institute of Modern Physics, Chinese Academy of Sciences, Lanzhou 730000, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
离散坐标 (Discrete coordinates, SN) 方法是中子输运方程数值求解的重要方法之一,由于其数值过程比较简单,对每个离散方向的计算过程都是相对独立的,可以编成适用于不同离散方向数的通用程序,给工程计算带来极大的方便。ANISN是国际上通用的一维、多群、带有一般各项异性散射的离散坐标程序,可用于一维平板、球和圆柱几何的中子和光子以及中子-光子的输运计算。与ANISN程序配套的BUGLE-80数据库是由美国原子能协会的ANS-6.1.2小组基于ENDF/B-IV库制作的ANISN格式的47群中子、20群光子、P3近似截面数据库,于1980年完成[1]。随着ENDF/B-Ⅶ.1、CENDL-3.1以及JENDL-4.0等最新评价数据库的相继释放[2],需要对ANISN截面库进行相应的更新。
麻省理工学院计算反应堆物理组开发的OpenMC程序,在进行中子堆芯输运的同时,提供了相应的勒让德散射分量的计数,能够给出从0-10阶的勒让德散射分量反应率,通过适当的处理及格式转化,可以输出符合特定堆芯能谱的中子群间散射截面,供给ANISN程序,以供进行确定论计算[3-4]。在计算过程中,OpenMC采用ENDF/B-Ⅶ.1库,群结构可以任意指定,此处采用了BUGLE-80的47群中子能群结构,并比较了不同能群结构划分对计算结果的影响。
近年来,随着核能的发展,对反应堆计算软件的需求也日益增加。目前国际上的研究热点方向逐渐从单一的物理计算、热工计算转换为物理和热工的耦合计算。相较于MCNPX等蒙特卡罗计算软件,由于确定论程序具有更快的计算速度,更加适合这类耦合计算,如近年来西安交通大学开发的物理-热工耦合程序LAVENDER即采用确定论程序用于堆芯物理计算[5]。而对于ANISN这类确定论计算程序,其截面库的制作是影响其计算精度的主要因素。除了用专门的多群截面制作程序如NJOY等制作截面外,原则上,可以利用蒙特卡罗程序通过计数能量和体积区间内的反应率及通量获得多群截面。但是目前广泛使用的MCNP、MCNPX、TRIPOLI等蒙特卡罗程序并不提供勒让德散射反应率的计数[6-8]。而新近开发的OpenMC,在计数中添加了高阶勒让德散射反应率的计数。本文即在此基础上,验证应用OpenMC制作多群截面及勒让德散射截面可行性,并将制作的截面提供给SN程序计算,验证计算结果的准确性。
1 计算方法确定论程序ANISN计算所需的群常数包括总截面、吸收截面、裂变截面和勒让德散射截面。基于Bugle-80数据库的中子能群结构,利用OpenMC计算总反应率、吸收反应率、裂变中子产生速率和高阶勒让德散射分量及相应的中子通量分布情况,通过程序的编写,实现核素多群截面及P0-P3阶勒让德散射截面的制作。
1.1 OpenMC程序简介OpenMC是由麻省理工学院 (Massachusetts Institute of Technology, MIT) 计算反应堆物理组于2011年开始研发的并行蒙特卡罗计算程序,其主要目的是开发一种能根据研究需要易扩展的高性能、免费开源的模拟计算程序,第一版在2012年12月发行。与一般MC (Monte Carlo) 程序不同,OpenMC输入文件格式是一系列的XML文件,以便于数据在不同程序和接口之间的交换。具体包括几何结构、材料定义、计算参数设置、计数类型、绘图及加速收敛设置等输入文件。为了实现多群截面及勒让德散射截面制作,需要在tallies卡中添加flux、absorption、nu-fission、total以及scatter-PN(或scatter-0, scatter-1, …, scatter-N)等计数,其中对scatter-PN计数需要同时输入入射能量区间和出射能量区间。
1.2 Pn截面计算及截面库制作在SN程序中,对于散射截面Σ(E'→E, Ω'→Ω) 按勒让德正交多项式展开:
| $ {\Sigma _s}(E' \to E, \Omega ' \to \Omega ) = {\Sigma _{n = 0}}\frac{{2n + 1}}{{4{\rm{\pi }}}}{P_n}({\mu _0}){\Sigma _{s, n}}(E' \to E) $ | (1) |
Pn截面或高阶勒让德分量是计算必须给定的参量。以一维问题多群问题为例,勒让德散射分量定义为:
| $ {\Sigma _{s, n, g' \to g}} = \frac{{\int_{{E_g}}^{{E_{g-1}}} {{\rm{d}}E\int_{{E_{g'}}}^{{E_{g''1}}} {{\rm{d}}E'} \int_z {{\phi _n}(z, E')} {\Sigma _{s, n}}(z, E' \to E){\rm{d}}z} }}{{\int_{{E_{g'}}}^{{E_{g'-1}}} {{\rm{d}}E'} \int_z {{\phi _n}(z, E')} {\rm{d}}zs}} $ | (2) |
式中:Σs, n和ϕn是使用勒让德多项式展开散射截面和中子通量的系数,由勒让德多项式的正交性求得。
OpenMC输出结果是文本格式文件,对通量和吸收反应率、裂变产生反应率和总反应率,给出各个能群内的数值;对勒让德散射分量,给出从一个能群散射到其他各个能群的各阶分量。
ANISN所需的截面库信息包括各群的吸收截面σa(g)、裂变产生截面ν·σf(g)、总截面σt(g) 和散射矩阵σs(g'→g)。对每一能群,其包含的数据数为Ngroup+3,其中群间散射截面从群内散射开始,向上散射截面为0。为直观说明其截面库格式,将其截面排布情况列于表 1(三群中子)。
| 表 1 ANISN截面库格式 Table 1 Structure of ANISN cross section library. |
接口程序通过读取OpenMC输出的各能群通量、反应率及勒让德散射分量,经过相除之后得到具体的截面数值,并输出ANISN格式的各阶勒让德散射截面及多群截面。过程中需要注意的是,对n阶勒让德分量,需要将OpenMC结果乘以展开系数2n+1。
2 基准题校验及分析基于GODIVA临界球问题,用OpenMC生成ANISN所需的P0-P3阶散射截面以及多群截面。由于ANISN只能计算一维情况,对圆柱几何,需要采用曲率修正因子,此处取为1.420892,在OpenMC计算中,上下边界取为反射边界条件,以使得计算结果更符合无限长圆柱的情况。计算过程中,ANISN计算精度取为10-4,OpenMC计算共500代,每代统计106个粒子,采用的数据库为ENDF/B-Ⅶ.1和CENDL-3.1,温度取为300 K。计算的几何模型参数及ANISN计算参数[9]列于表 2和3。
| 表 2 计算几何模型参数 Table 2 Geometry parameters of calculation model. |
| 表 3 ANISN主要计算参数 Table 3 Calculation parameters of ANISN. |
在ANISN计算中,划分一个区,30个节点,截面参数分别采用BUGLE-80(47群中子和20群光子)和OpenMC生成的截面数据,给出计算得到的有效中子增殖因子和中子通量结果的比对情况。
2.1 有效增殖因子计算利用OpenMC制作的多群截面及勒让德散射截面输入ANISN进行了确定论计算。结果表明,对GODIVA临界球,采用BUGLE-80截面库的ANISN计算结果与ENDF/B-Ⅶ.1库OpenMC计算结果相比偏差约为0.88%;而采用OpenMC制作的截面库的ANISN计算结果与OpenMC计算结果符合得很好,仅偏差约为0.10%。对圆柱几何,采用BUGLE-80和新制作的截面库与OpenMC计算结果分别相差0.71%和0.21%。使用CENDL-3.1和ENDF/B-Ⅶ.1两个数据库的计算结果基本一致,OpenMC蒙特卡罗计算结果相差在0.01%左右。两个数据库给出的有效增殖因子的计算结果与实验值相差在0.4%以内,计算结果较为准确。表 4中给出了采用两种数据库的蒙特卡罗计算结果与ANISN确定论计算结果的对比情况。
| 表 4 keff计算结果对比 Table 4 Comparison of keffcalculation. |
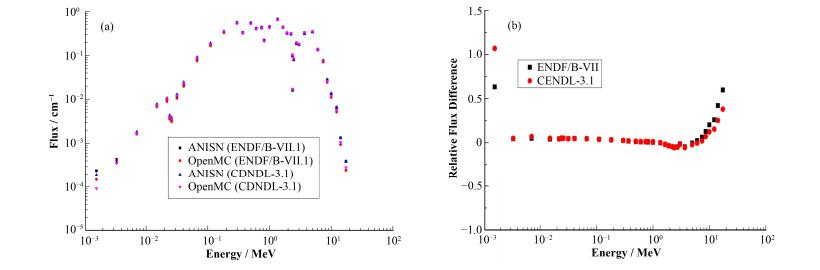
利用OpenMC和ANISN分别计算中子通量分布情况,将结果对比示于图 1。OpenMC计算采用ENDF/B-Ⅶ.1和CENDL-3.1数据库。从图 1可以看出,使用ANISN与OpenMC计算结果吻合得较好。为了更直观地看到ANISN计算中子能谱ϕB和ϕO与OpenMC计算得到的中子能谱ϕ之间的差异或符合程度,定义通量的相对差别Δϕr为:
| $ \Delta {\phi _{\rm{r}}} = ({\phi _{{\rm{B/O}}}}-\phi )/\phi $ | (3) |
|
图 1 通量计算结果对比 (a) 和通量相对差别 (b) Figure 1 Comparison of neutron flux calculation (a) and relative flux difference (b). |
图 1(b)给出ANISN使用不同数据库计算得到的Δϕr分布情况。可以看到,在中低能部分两者吻合得较好 (1 eV-10 MeV),在低能和高能部分与OpenMC计算结果相差较大,达到80%。其中,对相对差别小于5%之内的部分,其通量占据总通量的97.94%。由于能群划分较细(47群),差别可能是由于ANISN计算采用的是经过近似处理的多群截面,不能完全精确地保持连续截面的信息。此外,这部分能区的中子通量过小、统计误差较大也是原因之一。总体而言,其通量计算结果有较好的符合。
2.3 不同能群划分计算结果OpenMC可以输出任意数目能群的各阶勒让德散射分量,本文除制作了BUGLE-80 47群中子能群结构的截面库之外,还给出了3群、10群以及在BUGLE-80基础上添加了上限为20 MeV的48群截面库,以检验计算结果对群结构划分的敏感性,能群结构如表 5所示。计算中,ANISN输入文件中所需的各个能群的裂变谱由OpenMC计算给出,模型为GODIVA临界球。不同能群划分对有效增殖因子有影响,其相互差别约为1%。对于同样的能群数,不同的能群结构选择对其计算结果差别在千分之几,说明能群结构的选择对计算结果会有较大影响。表 5给出了利用ENDF/B-Ⅶ.1库制作的不同能群结构的ANISN计算结果及其与精细截面的蒙特卡罗计算结果的相对差别。
| 表 5 不同能群划分计算结果 Table 5 Results of different group structures. |
本文通过接口转换程序的制作,实现了开源蒙特卡罗程序OpenMC与确定论程序ANISN的耦合,验证了OpenMC应用于多群截面及勒让德散射截面制作中的可行性。针对GODIVA基准题,分别采用ENDF/B-Ⅶ.1及CENDLE-3.1数据库,统计了SN计算所需的多群截面及勒让德散射截面,并提供给ANISN进行确定论计算。结果表明,利用OpenMC统计的多群截面及勒让德散射截面的有效中子增殖因子与OpenMC采用连续能量截面的MC计算结果相差0.1%-0.2%,与实验值相差约0.32%,而能谱分布基本一致。这说明利用OpenMC为确定论程序ANISN提供所需截面是有效的,且计算结果有较高的精度。
利用OpenMC制作多群截面及勒让德散射截面,其确定论计算结果不仅依赖于划分的能群数目,还与能群结构的选择有关。计算结果表明对同样的能群数,其能群结构不同,计算结果会有千分之几的差别,而不同能群数目其计算结果差别约在1%。此外,由于采用OpenMC蒙特卡罗方法统计得到各个能群的反应率及通量之比得到截面,过程中会引入统计误差,尤其是通量较小的能群,这也会造成计算结果的偏差,可能是造成48群分群计算结果与蒙特卡罗计算结果偏差较大的原因。因而在实际应用中需要选择合适的能群结构及数目。
| [1] | Ward W E. A user manual for ANISN: a one dimensional discrete ordinates transport code with anisotropic scattering[R]. AEC Research and Development Report 81, 1967. DOI: 10.2172/4448708. |
| [2] | Zhang H, Wu H C. Benchmarking CENDL-3.1 with critical benchmarks[J]. Journal of the Korean Physical Society, 2011, 59(2): 1150–1153. DOI: 10.3938/jkps.59.1150 |
| [3] | Romano P K, Benoit F. The OpenMC Monte Carlo particle transport code[J]. Annals of Nuclear Energy, 2013, 51: 274–281. DOI: 10.1016/j.anucene.2012.06.040 |
| [4] | Siegel A R, Smith K, Romano P K, et al. Multi-core performance studies of a Monte Carlo neutron transport code[J]. International Journal of High Performance Computing Applications, 2014, 28(1): 87–96. DOI: 10.1177/1094342013492179 |
| [5] | Zhou S C, Wu H C, Cao L Z, et al. LAVENDER: a steady-state core analysis code for design studies of accelerator driven subcritical reactors[J]. Nuclear Engineering and Design, 2014, 278: 434–444. DOI: 10.1016/j.nucengdes.2014.07.027 |
| [6] |
刘萍. WIMS多群截面库更新时NJOY输入参数研究[J].
原子核物理评论, 2011, 18(3): 188–191.
LIU Ping. Study of NJOY input parameters for update of WIMS library[J]. Nuclear Physics Review, 2011, 18(3): 188–191. DOI: 10.3969/j.issn.1007-4627.2001.03.013 |
| [7] |
马纪敏, 刘永康, 李茂生. 次临界能源对用多群截面库的研制与校验[J].
核动力工程, 2012, 33(5): 16–21.
MA Jimin, LIU Yongkang, LI Maosheng. Development and validation of multi-group cross-section library for subcritical energy reactor[J]. Nuclear Power Engineering, 2012, 33(5): 16–21. DOI: 10.3969/j.issn.0258-0926.2012.05.004 |
| [8] |
李满仓, 王侃, 姚栋. 基于连续能量蒙特卡罗方法的均匀化群常数计算[J].
核科学与工程, 2012, 32(4): 306–314.
LI Mancang, WANG Kan, YAO Dong. Continuous energy Monte Carlo method based homogenization multi-group constants calculation[J]. Nuclear Science and Engineering, 2012, 32(4): 306–314. DOI: 10.3969/j.issn.0258-0918.2012.04.004 |
| [9] |
廖清富, 赵玉钧. ANISN程序使用手册[R]. 北京: 应用物理与计算数学研究所, 1988.
LIAO Qingfu, ZHAO Yujun. User manual of ANISN[R]. Beijing: Institute of Applied Physics and Computational Mathematics, 1988. |


