2. 中国科学院上海应用物理研究所 物理生物学研究室 嘉定园区 上海 201800;
3. 中国科学院大学 北京 100049
2. Division of Physical Biology, Shanghai Institute of Applied Physics, Chinese Academy of Sciences, Jiading Campus, Shanghai 201800, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
原子力显微术 (Atomic force microscopy, AFM) 自1986年发明以来[1],已经广泛应用于各类样品的形貌表征[2-3]和力学性质的测量[4-5]。其中,AFM的力曲线阵列模式 (Force volume mapping, FV)[6]是测量不同材料力学性能(形变量、杨氏模量、粘滞力等)有效的检测方法。FV模式的特点在于原子力显微镜的探针在接触样品过程中,探针悬臂部分的偏折与探针末端与样品间的相互作用力相关。一束激光投射在探针悬臂的背面,光电二极管记录激光的偏折信息,由此可获得探针与样品表面的力曲线,通过分析力-距离曲线得到样品的纳米力学性质。由于FV模式采用的是触发式,成像速度较慢,探针在样品上的作用力精准控制比较困难。由轻敲成像模式发展而来的力学成像模式-峰值力定量纳米力学模式 (Peak Force quantitative nanomechanical mapping, PF-QNM)[7]以峰值力作为反馈信号,而峰值力为设定的探针与样品间极小的相互作用力,所以该模式可准确控制探针作用在样品上的作用力,具有高速和高分辨率测量样品纳米力学性质的特点,可快速扫描样品,同时获得样品的形貌和力学性质信息,为精确测量生物膜[8]、蛋白质[9]和淀粉样纤维[10]等纳米级生物分子结构和力学性质提供了一条重要途径。
脱氧核糖核酸 (Deoxyribonucleic acid, DNA) 是重要的生物分子,承载着生物体的遗传信息,控制着生命体的活动。DNA分子是一种直径只有2.0 nm的长链状生物分子,它是由两条反向平行的DNA链盘旋而成的规则双螺旋立体结构[11]。由于其具备了独特的多样性、特异性和化学稳定性等特性,已经成为人们广泛研究的主题[12]。但是,尽管经历了许多年的研究,DNA分子的一些基本性质仍然没有被很好地理解,例如DNA分子的柔性或弹性等力学性质。在拥挤的细胞核环境中,DNA分子不可避免与液体或生物大分子相互碰撞,被动发生形变;DNA发挥作用时,需要发生构象变化进而与其他分子发生相互作用,这些都与DNA分子的力学性质密切相关[13]。杨氏模量是力学性能研究中最常用的参数之一,虽然已经有AFM测量单个DNA分子杨氏模量的方法[14],但是液体环境中DNA弹性测量未见报道。DNA分子弹性与自身以及周围环境水分子的含量有密切的关系,在液体环境下的DNA分子其弹性性质更加接近其结构的真实状态。实际上,DNA主要存在于细胞核中,且细胞核中DNA分子多是以超级结构“集合体”的形式存在,DNA双链以线状舒张状态存在的形式很少或者说并不多见。所以,本文以一种DNA自组装形式的DNA折纸为模型,测量DNA分子的杨氏模量,研究其弹性性质。DNA折纸术是由一条DNA长链和若干条DNA短链自组装形成的纳米结构,通过设计可获得形态各异的两维和三维的纳米图案[15]。通常两维的单层DNA折纸是由双链DNA交互排列而成,其理论高度为2 nm,此即为双链DNA分子高度,能够较好体现DNA链规则双螺旋的本质特性。但是如何在测量弹性的过程中,保证针尖有足够的压入深度同时又能够避免基底表面作用力的影响[16],准确高效地测量DNA的力学性质,依旧是一个值得探讨的问题。
本文利用AFM的PF-QNM模式,测量DNA样品弹性,研究峰值力对DNA折纸杨氏模量测量的影响,并与FV模式相比较,优化DNA折纸杨氏模量的测量方法。
1 材料与方法二维矩形图案的DNA折纸通常是一条长链和两百多条短链自组装形成[17],本实验所用长方形DNA折纸的自组装步骤简述如下:将长链DNA(单链脚手架链)与216条订书钉链DNA混合于TAE-Mg2+缓冲体系中,放入新加坡生产的PCR (Polymerase Chain Reaction) 仪中,从95 C退火至20 C,退火速率为0.1 C/10 s,获得DNA折纸后进行超滤。长链DNA为美国NEB公司的M13mp18噬菌体病毒单链DNA,订书钉短链DNA购于上海生物工程有限公司。用1×TAE/Mg2+缓冲液(40mmol·L-1 Tris-乙酸、1 mmol·L-1乙二胺四乙酸 (EDTA)、12.5mmol·L-1 MgCl2,pH 8.0),将超滤完成后的DNA折纸稀释到10 nmol,-20 C储存备用。制备AFM样品时,取2 µL的DNA折纸滴于新解离的云母上,吸附5 min后,将样品放在载物台上,加入30 µL 1×TAE/Mg2+缓冲液后,用于AFM成像。
AFM采用的是德国Bruker公司NanoScope Ⅷ系统,在PF-QNM和FV模式下获取数据。扫描管为J头,探针采用Bruker公司型号为Scanasyst-FLUID+的针尖。成像温度为25 C左右。液相环境条件下,在Bruker公司提供的蓝宝石上校准探针偏折灵敏度,用AFM系统自带软件Thermal Tune功能确定探针的弹性常数 (k),使用布鲁克 (Bruker) 公司提供的已知杨氏模量的标准样品校准针尖的半径 (R)。我们采用PF-QNM的直接法获得样品的弹性模量。
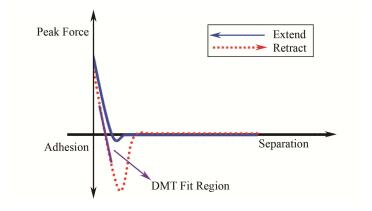
2 实验结果与讨论 2.1 PF-QNM力曲线分析和杨氏模量计算PF-QNM力曲线是力学成像模式获得杨氏模量的原理基础,图 1是PF-QNM的力-距离曲线,横坐标表示探针与样品间的距离,纵坐标表示探针与样品间的作用力,正方向表示峰值力的大小,负方向表示粘滞力,图 1中Extend曲线表示探针靠近样品表面时力和距离的关系,Retract曲线表示探针离开样品表面时力与距离的关系。为了避免趋近曲线中样品塑形形变部分的影响,采用Retract曲线获取样品的弹性形变。利用这部分弹性形变与力的关系,拟合这部分数据,定量计算样品的杨氏模量[18]。
|
图 1 力曲线示意图 Figure 1 Sketch of force-distance curve. |
杨氏模量的计算,选择合适的物理模型对力曲线数据进行拟合是首要关键步骤。因为实验条件的不同和样品材料的多样性和特殊性,需要考虑探针接触样品表面时的各种相互作用的差异(主要是粘滞力[19]),可以将探针与样品之间的接触物理模型分为Hertz模型、Sneddon模型、Johnson-Kendall-Roberts (JKR) 模型和Derjaguin-Mrjagui-Toporov (DMT) 模型。Hertz和Sneddon模型是两种本质上相同的模式,它们是不考虑接触面间的相互作用,以针尖-样品之间的相互作用为线性弹性关系。原始Hertz模型仅适用于半球状针尖,后来Sneddon模型对其进行了扩展,将其它轴对称几何形状(圆锥)的针尖也包含在内,丰富了探针形状的选择。JKR模型适用于针尖和样品之间除了有弹性相互作用之外,还有较强的粘合接触。DMT模型适用于粘附力较弱但仍可测到的样品,以及和与样品压痕深度相比针尖半径相对较小的样品最为有效[20]。在动态扫描过程中,样品与探针之间的粘滞力很小[21],涉及相对较弱的粘附力和较小的针尖半径,因此DMT模型更适用于DNA弹性研究。其公式如下:
| $ F - {F_{{\rm{adh}}}} = \frac{4}{3}{E^*}\sqrt {R \cdot d} $ | (1) |
式中:F是AFM施加的负载力;Fadh是样品的粘滞力;R是针尖半径;d是样品的形变量;E*是简约杨氏模量。其中E*可以由式 (2) 得到:
| $ {E^*}{\rm{ = }}{\left( {\frac{{1{\rm{ - }}\upsilon _{\rm{s}}^{\rm{2}}}}{{{E_{\rm{s}}}}} + \frac{{1{\rm{ - }}\upsilon _{\rm{t}}^{\rm{2}}}}{{{E_{\rm{t}}}}}} \right)^{ - 1}} $ | (2) |
式中:
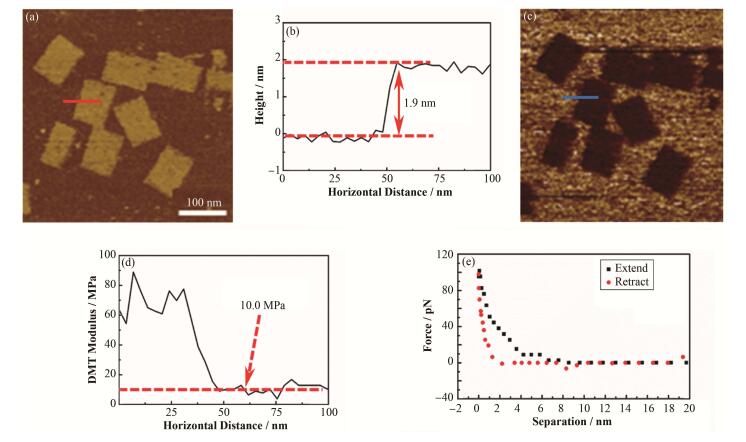
在AFM的PF-QNM模式下,不仅可以获得样品的高分辨率形貌图,还可以获得包含样品力学性质的信息。图 2(a)和(c)分别为DNA折纸的形貌图和DMT杨氏模量图(峰值力100 pN)。AFM形貌图中(图 2(a)),DNA折纸和云母衬底差别明显。DNA折纸呈现为长方形,横线处高度测量值约为1.9 nm(图 2(b)),与设计的几何形状相符合。杨氏模量图中(图 2(c))可以观察到两部分弹性杨氏模量,一部分为较硬的白云母,另一部分为DNA折纸,质地较软。横线处模量约为10.0 MPa(图 2(d))。杨氏模量图中(图 2(c)和(d)),虽然云母和DNA折纸可很好地区分,但是测量获得的云母基底杨氏模量在70 MPa左右,与云母的实际值不符。造成这个现象的原因可能是100 pN的小力对较硬的云母不能达到足够的压入深度[20]。当AFM测量样品的杨氏模量,AFM的探针是否压入样品足够的深度,是非常重要的物理信息。要保证足够的压入深度,除了选择合适的探针外,在PF-QNM模式下也需要选取合适大小的峰值力。图 2(e)是图 2(a)在快速扫描过程中的云母和DNA折纸的力曲线(图 2(e)为DNA折纸上某点的力曲线)。
|
图 2 原子力显微镜形貌图像 (a) 和高度信息图 (b)、DMT杨氏模量图像 (c) 和信息图 (d)、DNA折纸的力-距离曲线图 (e) Figure 2 AFM topography image (a) and cross section profile (b), AFM DMT modulus image (c) and cross section profile (d), force-distance curve of DNA origami (e). |
PF-QNM模式能精确控制峰值力大小,同时获得弹性杨氏模量的图像,使获得样品模量值的过程更加快速便捷。对于只有2 nm高度的DNA折纸生物样品,在测量过程中,探针压入的深度对于DNA折纸杨氏模量的测量具有非常大的影响[22]。所以,选取合适的峰值力对测试小分子生物样品的弹性杨氏模量至关重要。也就是说,我们要准确定量测量DNA的弹性杨氏模量,寻找到合适力区间是非常重要的。
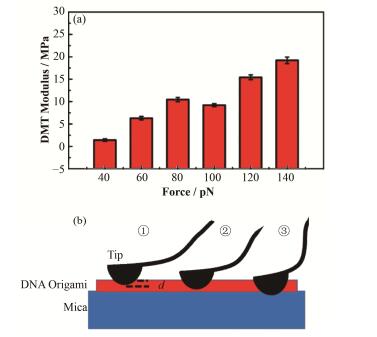
为了寻找测量DNA弹性的最佳峰值力,测量中对同一DNA折纸样品,改变峰值力大小,观察DNA折纸的DMT杨氏模量变化趋势。统计结果表明(图 3(a)),当设定的峰值力为60-100 pN时,DNA折纸的杨氏模量变化不大。当峰值力增大到140pN时,DNA折纸的弹性杨氏模量的测量值显著增加,可达到20.0 MPa左右,而峰值力降低到40 pN时,DNA折纸的弹性显著减小。从力-距离曲线中,可以获得样品在受到不同力作用下的形变。当AFM峰值力较小在40 pN时,DNA的弹性杨氏模量显著减小。这可能由于峰值力太小,造成探针压入DNA折纸深度不够,如图 3(b)中第一种探针与样品压入位置深度关系所示;当峰值力在140pN时,由于力过大,导致探针压入形变受到基底云母的影响,造成实际的DNA模量值被掩埋,如图 3(b)中第三种情形。当峰值力在80-100 pN时,探针压入DNA折纸深度相对合适,如图 3(b)中第二种情况,结合模量值与峰值力关系,可得出该力区间所测的DNA杨氏模量值较为准确,并且稳定性好。
|
图 3 不同峰值力DNA折纸的弹性杨氏模量 (a) 和三种针尖压入折纸深度的示意图 (b) Figure 3 The DMT modulus of DNA origami as a function of peak force (a) and sketch of the three kinds of indentation of tip pressuring on DNA origami (b). |
传统的FV模式广泛应用于生物、医学和材料等领域,在FV模式下得到的力曲线更能反映样品真实的物理特性[23]。
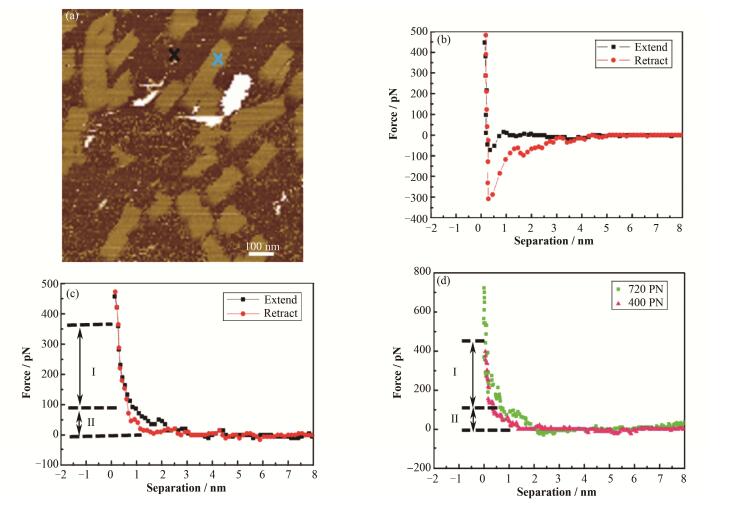
图 4(a)是FV模式形貌图,图 4(b)是图 4(a)中黑色叉处的力曲线,即探针作用白云母的力-距离曲线,图 4(c)是图 4(a)中折纸处的力-距离曲线,即探针作用在DNA折纸的力-距离曲线。在图 4(b)中,Extend曲线表示探针靠近白云母表面时力与距离的关系曲线,Retract曲线表示探针离开白云母表面时力与距离的关系曲线。比较图 4(b)和图 4(c)中的Retract曲线,并进行DMT杨氏模量的拟合,图 4(b)中,Retract曲线部分线性好,反映的是白云母的弹性杨氏模量,拟合值为4.5 GPa;图 4(c)中的折纸的Retract曲线可以观察到斜率不一样的曲线,可大致分为两部分:Ⅰ区和Ⅱ区。曲线Ⅰ区的对应拟合的力区间在100-400 pN,形变量在0.5 nm,根据DMT拟合的弹性杨氏模量是450MPa。在这部分力区间内,所测得杨氏模量明显高于Ⅱ区部分。而在曲线Ⅱ区的对应拟合的力区间是0-100pN,形变量在1.2nm,拟合的弹性杨氏模量为10.0 MPa左右。综合DNA折纸的特点,高度为2.0nm。可以认为,Ⅱ区的弹性杨氏模量就是DNA折纸的杨氏模量,Ⅰ区部分的力曲线是固体基底白云母和DNA折纸共同作用的结果。而且通过观察多条DNA折纸上的力曲线,此现象比较明显,并非偶然现象。图 4(d)中分别为400 pN和720pN作用力条件下的力曲线,发现在100pN以下区间拟合杨氏模量在10.0 MPa左右,400 pN力曲线拟合数据为10.3 MPa,720 pN力曲线拟合数据为8.9 MPa。说明在不同的力作用下,拟合力曲线中力为0-100 pN,可以得到DNA折纸的弹性模量约为10 MPa。以上结果显示,尽管两种力学测量模式成像有些差异,但在一定范围内获得的DNA折纸的力学测量数据相近似。
|
图 4 FV原子力显微镜形貌图像 (a)、白云母表面上的力-距离曲线 (b)、DNA折纸的力-距离曲线 (c)、DNA折纸分别受到400 pN和720 pN条件下,探针离开DNA折纸表面时的力曲线 (d) Figure 4 FV topography AFM image (a), force-distance curve of mica (b), force-distance curve of DNA origami (c), retract curves of DNA origami under the force of 400 pN and 720 pN, respectively (d). |
DNA是重要的长链状生物分子,其弹性与结构和功能密切相关。本文将AFM的力学性质测量与DNA折纸技术相结合,建立了一种新颖可靠的定量测量DNA分子杨氏模量的方法。通过AFM的PF-QNM模式,获得了液体环境中DNA折纸的杨氏模量,发现当峰值力区间为80-100 pN时,测量结果较为准确和稳定。AFM的PF-QNM模式与传统的力学性质测量模式FV相比较显示两种力学性质测量模式各有特点。对于DNA折纸来说,只有在合适的针尖与样品相互作用力范围内,获得的杨氏模量才比较可靠。本文测量的DNA折纸的杨氏模量约为10 MPa,随着样品与探针间的作用力有所改变,说明生物材料有较大的弹性、易形变,提示在对微小的生物薄样品进行定量力学性质测定时,需要控制作用力的范围,这对其他生物分子弹性测量具有借鉴的意义。
| [1] | Binnig G, Quate C F, Gerber C. Atomic force microscope[J]. Physical Review Letters, 1986, 56(9): 930–933. DOI: 10.1103/PhysRevLett.56.930 |
| [2] | Kong L X, Wang L J, Su L L, et al. Amyloid fibril-supported Pd nanoparticles as electrocatalyst for hydrogen peroxide reduction[J]. Nuclear Science and Techniques, 2016, 27(4): 97. DOI: 10.1007/s41365-016-0098-2 |
| [3] |
杨硕, 汪颖, 杨海军, 等. 云母-石墨烯界面纳米尺度受限水层的湿润-去湿润研究[J].
核技术, 2016, 39(7): 070501.
YANG Shuo, WANG Ying, YANG Haijun, et al. Studies on wetting-dewetting process of molecularly thin water adlayer confined between graphene and mica interface[J]. Nuclear Techniques, 2016, 39(7): 070501. DOI: 10.11889/j.0253-3219.2016.hjs.39.070501 |
| [4] |
王牡, 蔡继业. 原子力显微镜在生物分子力学性质方面的研究[J].
现代科学仪器, 2010, 26(1): 118–121.
WANG Mu, CAI Jiye. Application of atomic force microscope concerning mechanical properties of biological molecules[J]. Modern Scientific Instruments, 2010, 26(1): 118–121. |
| [5] | Liu K, Song Y, Feng W, et al. Extracting a single polyethylene oxide chain from a single crystal by a combination of atomic force microscopy imaging and single-molecule force spectroscopy: toward the investigation of molecular interactions in their condensed states[J]. Journal of the American Chemical Society, 2011, 133(10): 3226–3229. DOI: 10.1021/ja108022h |
| [6] | Radmacher M, Cleveland J P, Fritz M, et al. Mapping interaction forces with the atomic force microscope[J]. Biophysical Journal, 1994, 66(6): 2159–2165. DOI: 10.1016/S0006-3495(94)81011-2 |
| [7] | Guzman H V, Perrino A P, Garcia R. Peak forces in high-resolution imaging of soft matter in liquid[J]. ACS Nano, 2013, 7(4): 3198–3204. DOI: 10.1021/nn4012835 |
| [8] | Picas L, Rico F, Scheuring S. Direct measurement of the mechanical properties of lipid phases in supported bilayers[J]. Biophysical Journal, 2012, 102(1): 1–3. DOI: 10.1016/j.bpj.2011.11.4001 |
| [9] | Voss A, Dietz C, Stocker A, et al. Quantitative measurement of the mechanical properties of human antibodies with sub-10-nm resolution in a liquid environment[J]. Nano Research, 2015, 8(6): 1987–1996. DOI: 10.1007/s12274-015-0710-5 |
| [10] | Wang L J, Kong L X, Su L L, et al. Nanomechanical properties of amyloid fibrils formed in a water nanofilm on mica surface[J]. Chinese Physics Letters, 2016, 33(1): 018702. DOI: 10.1088/0256-307x/33/1/018702 |
| [11] | Wilkins M H F, Storkes A R, Wilson H R. Molecular structure of nucleic acids: molecular structure of deoxypentose nucleic acids[J]. Nature, 2003, 421(6921): 398–400. DOI: 10.1038/171738a0 |
| [12] | Yuan C, Chen H, Lou X W, et al. DNA bending stiffness on small length scales[J]. Physical Review Letters, 2008, 100(1): 145–150. DOI: 10.1103/PhysRevLett.100.018102 |
| [13] | Hogan M E, Austin R H. Importance of DNA stiffness in protein DNA-binding specificity[J]. Nature, 1987, 329(6136): 263–266. DOI: 10.1038/329263a0 |
| [14] | Zhou X F, Sun J L, An H J, et al. Radial compression elasticity of single DNA molecules studied by vibrating scanning polarization force microscopy[J]. Physical Review E: Statistical, Nonlinear, and Soft Matter Physics, 2005, 71(6 Pt 1): 062901. DOI: 10.1103/PhysRevE.71.062901 |
| [15] | Rothemund P W. Folding DNA to create nanoscale shapes and patterns[J]. Nature, 2006, 440(7082): 297–302. DOI: 10.1038/nature04586 |
| [16] | Perrino A P, Garcia R. How soft is a single protein? The stress-strain curve of antibody pentamers with 5 PN and 50 pm resolutions[J]. Nanoscale, 2016, 8(17): 9151–9158. DOI: 10.1039/c5nr07957h |
| [17] | Ke Y, Lindsay S, Chang Y, et al. Self-assembled water-soluble nucleic acid probe tiles for label-free RNA hybridization assays[J]. Science, 2008, 319(5860): 180–183. DOI: 10.1126/science.1150082 |
| [18] | Pittenger B, Erina N, Su C. Mechanical property mapping at the nanoscale using peakforce QNM scanning probe technique[M]. Springer Netherlands, 2014, 203: 31-51. DOI: 10.1007/978-94-007-6919-9-2. |
| [19] | Derjaguin B V, Muller V M, Toporov Y P. Effect of contact deformations on the adhesion of particles[J]. Journal of Colloid & Interface Science, 1975, 53(2): 314–326. DOI: 10.1016/0021-9797(75)90018-1 |
| [20] | Butt H J, Cappella B, Kappl M. Force measurements with the atomic force microscope: technique, interpretation and applications[J]. Surface Science Reports, 2005, 59(1-6): 151–152. DOI: 10.1016/j.surfrep.2005.08.003 |
| [21] | Tsukruk V V, Shulha H, Zhai X W. Nanoscale stiffness of individual dendritic molecules and their aggregates[J]. Applied Physics Letters, 2003, 82(6): 907–909. DOI: 10.1063/1.1544056 |
| [22] | Adamcik J, Berquand A, Mezzenga R. Single-step direct measurement of amyloid fibrils stiffness by peak force quantitative nanomechanical atomic force microscopy[J]. Applied Physics Letters, 2011, 98(19): 193701. DOI: 10.1063/1.3589369 |
| [23] | Smolyakov G, Formosa-dague C, Severac C, et al. High speed indentation measures by FV, QI and QNM introduce a new understanding of bionanomechanical experiments[J]. Micron, 2016, 85: 8–14. DOI: 10.1016/j.micron.2016.03.002 |


