氡析出是氡穿过两相介质界面的现象和过程，氡析出率是单位时间内穿过单位面积界面析出的氡量^[1-3]。氡析出率测量是铀矿冶废石场、尾矿库防氡覆盖治理的关键，也是铀矿通风、环境污染及治理中寻找源项的关键，其中包括地下军事工程和民用建筑内的氡污染治理，目前在我国已引起普遍关注^[4-8]。研究氡析出率快速测量是辐射防护领域中的一项重要的工作。

静电收集α能谱法是测量氡析出率的主流发展方向^[9-13]。南华大学研制的NRE-I型便携式氡析出率自动测量仪采用高灵敏探测效率的静电收集方式，能够快速测量介质表面的氡析出率，其105 min的测量结果与南华大学氡析出率标准装置参考值的相对偏差在5%以内^[14-15]。但对氡析出率标准装置快速测量以“相对偏差”分析测量结果已不适应国际交流的需要，需结合不确定度原理，通过分量量化实验结果，完善氡析出率快速测量结果的可信程度。为世界各国氡析出率测量及其所得到的结果可以进行相互比对，有必要对氡析出率测量结果进行不确定度评定^[16]。随着测量不确定度理论的发展，将氡析出率测量的数据处理与不确定度评定相结合，提高测量结果的科学性、准确性是主要的研究方向^[17]。为确保快速测量方法的准确性、可靠性和溯源性，本文结合氡析出率快速测量不确定度原理，利用南华大学研制的NRE-I便携式氡析出率自动测量仪对氡析出率快速测量方法引入的不确定度进行分析和评定，开展了氡析出率快速测量方法的可靠性研究。

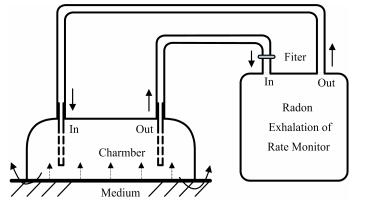
根据国际原子能机构 (International Atomic Energy Agency, IAEA) 333号技术丛书《铀尾矿氡析出测量与计算》（1992）中给出了氡析出率测量最常用的积累法（又称局部静态法）^[18-19]，即在待测介质表面扣一集氡室，周边用不透气材料密封，通过两根硅胶管与NRE-I便携式氡析出率测量仪的测量腔进行连接，实验装置图如图 1所示。

图 1

图 1 氡析出率快速测量实验装置图 Figure 1 Experimental setup of rapid determination for standard device of radon exhalation rate.

采用等时间间隔取样，以T为测量周期进行连续测量，根据集氡室内单位时间内氡浓度变化^[19]：

式中：J为氡析出率，Bq·m^-2·s^-1；S为集氡室底面积，m²；V为集氡室、硅胶连接管和氡析出率测量腔的总体积（简称收集总体积），m³；T为测量周期，s；C为集氡室中的氡浓度，Bq·m^-3； $ \lambda $为氡的衰变常量，2.1×10^-6 s^-1；R为泄漏和反扩散率，s^-1。

根据相邻两测量周期测量集氡室中氡浓度的关系：

通过多次测量提高测量精度，用最小二乘法线性拟合得到截距a、斜率b后求出氡析出率J^[20]。

其中：

氡析出率快速测量结果计算依据式 (2)，由式 (2) 可知，影响氡析出率测量结果的不确定度的来源有：a、b、V、T、S和n，其中a、b值的不确定度来源于测量的氡浓度C_n以及测量的次数n。

由于各分量a、b、T、V、S互不相关，氡析出率J的测量结果合成标准不确定度^[21]：

其中各分量的传播系数：

线性拟合参数a、b的不确定度包括A类不确定和B类不确定。其中A类是用对观测列的氡浓度C_n进行的统计分析，而B类是用不同于对观测列氡浓度C_n测的系统不确定度进行的统计分析。

式 (3)、(4) 中截距a和斜率b的A类标准不确定度分量为：

其中：

其实验标准差：

测量数据C_n+1和C_n具有相同B类不确定度u_B(C_n)、u_B(C_n+1)，由于C_n+1及C_n的测量数据序列各测量值之间存在相关性，按照求和法进行合成，可得斜率b的B类总不确定度：

式中：u_B(C_n)、u_B(C_n+1) 具有相同的不确定度，南华大学标准氡室相对不确定度u_B(C_n+1)=2.9%，则斜率b的B类总不确定度u_B(b)=$ \sqrt 2 $u_B(C_n+1)= 0.041。

由于实验数据的分布符合均匀分布，且数据分布上下限比值趋于无穷大，截距a的u_B(a) ≈0。

截距a和斜率b的合成标准不确定度为：

采用A类方法评定，与重复性有关的合成标准不确定度均包含其中。对收集总体积进行5次重复性测定，所得结果如下：5712 mL、5735 mL、5731mL、5720 mL、5727 mL，平均值5725mL。收集总体积的重复测量数据的实验标准差为：

则：

根据JJF1059.1-2012《测量不确定度评定与表示》的规定，用1000 mL的量筒进行测量收集总体积，其量筒的最大允许误差1 mL，以三角分布估算量筒校准引入的相对不确定度。量筒校准的标位偏差为u(V₁)=$ 1/\sqrt 6 $=0.408 mL。

V的标准不确定度$ {u_c}(V) = \sqrt {{u_A}{{(V)}^2} + {u_B}{{(V)}^2}} $=1.30 mL=1.30×10^-6 m^-3。

对于NRE-I氡析出率测量仪，快速测量氡析出率时其测量周期T=15 min，重复性测量周期选择T=900 s进行10次测量，所得数据为900.41 s、901.33 s、900.87 s、901.80 s、901.32 s、901.76 s、901.35 s、901.52 s、901.43 s、901.32 s，其平均值为901.30 s。测量周期重复测量数据的实验标准差为：

则：

根据JJG601-2003时间检定仪的规程，秒表检定仪的准确度在1×10^-7 s，u_B(T)=1×10^-7/$ \sqrt 3 $= 6.671×10^-8s，因此可忽略不计。

T的标准不确定u_c(T)=u_A(T)=0.236 s。

集氡室的底部直径d的重复性测量进行5次测量，所得数据为291.5 mm、291.0 mm、292.0 mm、292.0 mm、291.5 mm，因此平均值为291.6 mm。其直径重复测量数据的实验标准差为：

则：

S的计算模型参考JJF1059.1-2012《测量不确定度评定与表示》的规定，采用S=$ {\rm{\pi }}$(d/2)²=0.25 $ {\rm{\pi }}$d²计算模型，S的标准不确定度u(S)=0.25pu(d)。

直径d用米尺测量，其最大允许误差是1 mm，即u_B(d)=1 mm。

底部直径d的标准不确定度：

集氡室底面积的标准不确定度u_c(S)= 0.25$ {\rm{\pi }}$u(d)= 0.855 mm²=8.55×10^-7 m²。

南华大学氡实验室建立了一套氡析出率标准装置，提供了析出率稳定的测量对象，其氡析出率的参考值是用闪烁室法和活性炭盒 ${\rm{\gamma }} $谱法共同测定的，1号标准装置的氡析出率参考值为 (1.48±0.05) Bq·m^-2s^-1，2号标准装置的氡析出率参考值为 (2.60±0.08) Bq·m^-2·s^-1，3号标准装置的氡析出率参考值为 (0.39±0.02) Bq·m^-2·s^-1。快速测量方法在1-3号标准装置上的测量结果如表 1所示。

表 1

表 1 1−3号标准装置不确定评定结果 Table 1 Evaluation of uncertainty in the 1−3# standard device. 各分量参数 Each component 不确定度传播系数 Propagation coefficient of uncertainty 各分量标准不确定度 Standard uncertainty in each corresponding component 不确定度评定结果 Evaluation of uncertainty 1号 1# a=1.17×104 ∂J/∂a=1.30×10−4 uc(a)=6.16×102 合成标准不确定度 Composite standard uncertain uc(J)=0.12 Bq·m−2·s−1 相对合成标准不确定度 Relative composite standard uncertain uc= u(J)/J=8.00% b=8.10×10-1 ∂J/∂b=-2.43 uc(b)=3.77×10−2 V=5.73×10-3 m3 ∂J/∂V=2.67×102 uc(V)=1.30×10-6 m-3 T=9.00×102s ∂J/∂T=-1.69×10-3 uc(T)=0.236 s S=6.67×10-2 m2 ∂J/∂S=-22.7 uc(S)=8.55×10-7 m2 2号 2# a=2.58×104 ∂J/∂a=1.04×10-4 uc(a)=1.28×103 合成标准不确定度 Composite standard uncertain uc(J)=0.21 Bq∙m-2∙s-1 相对合成标准不确定度 Relative composite standard uncertain uc= u(J)/J=7.79% b=8.54×10-1 ∂J/∂b=-4.20 uc(b)=3.81×10-2 V=5.73×10-3 m3 ∂J/∂V=4.68×102 uc(V)=1.30×10-6 m-3 T=9.00×102s ∂J/∂T=-2.97×10-3 uc(T)=0.236 s S=6.67×10-2 m2 ∂J/∂S=-40.5 uc(S)=8.55×10-7 m2 3号 3# a=3.52×103 ∂J/∂a=1.04×10-4 uc(a)=2.93×102 合成标准不确定度 Composite standard uncertain uc(J)=0.04 Bq∙m-2∙s-1 相对合成标准不确定度 Relative composite standard uncertain uc= u(J)/J=11.03% b=7.60×10-1 ∂J/∂b=-6.19×10-1 uc(b)=4.43×10-2 V=5.73×10-3 m3 ∂J/∂V=66.7 uc(V)=1.30×10-6 m-3 T=9.00×102s ∂J/∂T=-4.22×10-4 uc(T)=0.236 s S=6.67×10-2 m2 ∂J/∂S=-5.76 uc(S)=8.55×10-7 m2

表 1 1−3号标准装置不确定评定结果 Table 1 Evaluation of uncertainty in the 1−3# standard device.

表 1结果表明，1号氡析出率标准装置的结果J=(1.52±0.12) Bq·m^-2·s^-1，其相对不确定度为8.00%；2号氡析出率标准装置的结果J=(2.67±0.21) Bq·m^-2·s^-1，其相对不确定度为7.79%；3号氡析出率标准装置的结果J=(0.38±0.04) Bq·m^-2·s^-1，其相对不确定度为11.03%。

表 1的结果显示，在氡析出率0.39-2.62Bq·m^-2·s^-1的标准装置上采用快速测量方法对氡析出率标准装置进行快速测量，其结果的标准不确定度均比标准装置提供的不确定度要大，由于放射性测量存在统计涨落，在样本含量较小、测量时间短的情况下，快速测量方法的测量结果比标氡析出率标准装置定值结果的不确定度大，符合放射性测定的概率统计。但三个标准装置上快速测量的相对不确定度均在12%以内，且随着氡析出率的增大，其不确定度降低。

本文从氡析出率测量原理出发，建立氡析出率标准装置快速测量的不确定度理论分析模型，在不确定度概念的具体化和量化基础上，对氡析出率标准装置快速测量不确定度的来源进行分析及评定。较好地解决了传统评价氡析出率结果的单一性和不合理性。通过引入了最小二乘法线性拟合获得线性参数a、b的值，实现了氡析出率快速计算，对不确定度分析模型分量的不确定度进行分析，在南华大学建立的0.39-2.62 Bq·m^-2·s^-1氡析出率标准装置上，105min测量的结果其相对合成标准不确定度均不超过12%。为氡析出率快速测量方法的置信程度评定提出了新的评价方法。