2. 中国科学院等离子体物理研究所 合肥 230031;
3. 中国科学技术大学 核科学技术学院 合肥 230026
2. Institute of Plasma Physics, Chinese Academy of Sciences, Hefei 230031, China;
3. School of Nuclear Science and Technology, University of Science and Technology of China, Hefei 230026, China
1977年,Isler[1]首次在橡树岭国家实验室托卡马克装置上观察到氢中性束与完全剥离的氧离子发生电荷交换产生的谱线,经过几十年的发展,电荷交换复合光谱 (Charge eXchange Recombination Spectroscopy, CXRS) 诊断逐步发展成为核聚变装置上测量等离子体离子温度和旋转速度的常规诊断之一[2-7]。CXRS诊断是通过测量注入的高能氘 (D) 中性粒子与等离子体中完全电离的碳离子 (C6+) 电荷交换所辐射出的CVI (529.059 nm,n=8→7) 谱线的多普勒展宽和频移分别计算等离子中C6+杂质的温度以及旋转速度。在实际测量中,除了谱线本身的多普勒展宽外,光谱仪仪器展宽的影响不可避免,其与真实光谱的卷积会导致谱线明显变宽,需要通过反卷积的方法将仪器函数扣除,还原真实谱线,进而提高离子温度的测量精度。关于反卷积算法,此前很多人使用过MAP (Maximum a Posteriori) 算法[8-9]、Gold算法[10]、盲反卷积[11-12]等方法进行处理。但是这些算法在数据处理上存在一定缺陷,如MAP方法的缺点就是会存在数据拟合过度,致使算法失效等;Gold算法存在收敛速度慢导致计算时间过长的问题;而盲反卷积则会产生噪声放大等问题。本文采用了贝叶斯方法[13-15]进行光谱的反卷积,这种方法不仅可以使我们更容易得到一些相关的先验信息,而且可以有效地避免病态问题,同时可以使用控制迭代次数的方法有效控制噪声放大问题。
本文首先介绍实验准备工作,包括先进实验超导托卡马克 (Experimental Advanced Superconducting Tokamak, EAST)[16]以及EAST上边界CXRS系统的系统介绍、仪器函数的获取以及从贝叶斯条件概率公式推导出贝叶斯反卷积的表达式,然后再分别从仿真模拟以及EAST实验来验证贝叶斯反卷积方法的可行性,最后对经过反卷积处理后的实验光谱进行谱线拟合,并进行了相应的杂质谱线识别工作。
1 实验部分 1.1 实验准备EAST具体参数:大半径R约为1.752 m,小半径a约为0.45 m,纵场BT=1.5-3.0 T,等离子体电流Ip约为1 MA,并且可以在下单零、双零、上单零三种偏滤器位形下运行。EAST内真空室第一壁材料采用钼,上下偏滤器分别采用钨和碳材料,辅助加热天线材料涉及不锈钢和铜。另外内真空室还可能存在壁处理残余气体氦和氧,或进行了锂和硅涂层壁处理,诊断及特殊实验时注入氩。因此放电过程等离子体中可能存在的本征杂质和注入杂质涵盖了从低Z到高Z元素He、Li、C、O、Si、Ar、Fe、Cu、Mo和W等。
EAST上边界CXRS诊断系统 (edge CXRS, eCXRS) 布局如图 1所示。EAST上同向中性束注入系统位于A窗口赤道面上[17],eCXRS系统位于P窗口水平中平面上,主要由远心聚焦镜头、光纤束、光谱仪[18](镜头F数为2.8,焦距f=400 mm,光栅刻线为2160 mm-1)以及电子倍增电荷耦合元件 (Electron Multiplying Charge Coupled Device, EMCCD) 构成。
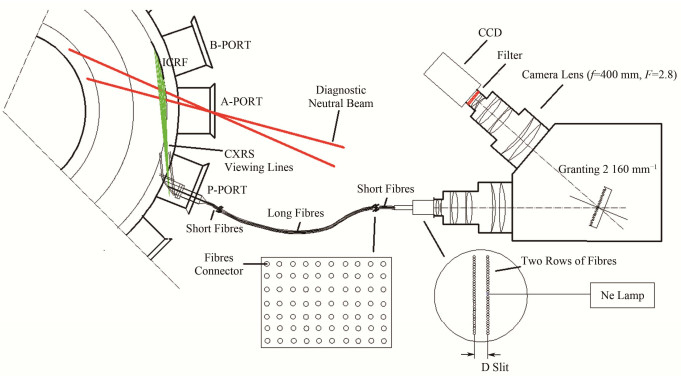
|
图 1 边界电荷复合交换诊断系统示意图 Figure 1 Schematic layout of the eCXRS system on EAST |
光谱仪是将成分复杂的光分解为光谱线的科学仪器。在实际操作当中光谱仪本身不可避免地存在衍射效应,又总是在一定缝宽下使用,此外还存在像差、仪器调整误差、探测器像元有限尺寸等影响,这些会使在焦平面上的探测器阵列测得的光谱发生变形现象,如谱线变宽等。对于线性系统,这种效应在数学上可以用卷积运算来描述,光谱仪对信号加工所用信息可以用一个称为仪器函数 (Instrument Function, IF) 的数学模型来描述,测量信号就是真实信号与仪器函数的卷积加上噪声。因此为了得到真实的谱线,需要进行反卷积处理。同时需要选择离待测谱线靠近的标准灯谱线,才能准确地进行反卷积。本文采用的IF是使用标准灯氖光源发出的Ne Ⅰ谱线进行谱线拟合得到,并且选取的Ne Ⅰ谱线(即λ=529.8189 nm)尽量靠近诊断需要测量的CVI (529.059 nm,n=8→7) 谱线,整个光谱采用同一个IF函数来进行反卷积。
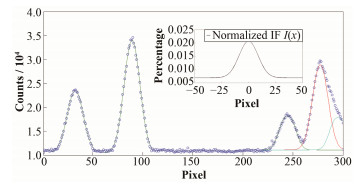
获取IF的方法如图 2所示,将氖标准灯光源通过短光纤向光谱仪端打光,利用CCD相机采集Ne谱线。CCD相机上对应通道采集结果如图 3所示,对应谱线分别为530.4756nm、529.8189nm、528.0085nm、527.4039nm Ne Ⅰ一级谱线以及263.8095nm Ne Ⅰ二级谱线。选取第二条Ne Ⅰ谱线 (λ=529.8189nm),使用矩阵函数Ii进行拟合:

|
图 2 通过标准灯Ne获取IF Figure 2 Wavelength calibration by neon pen ray lamp |
|
图 3 氖光源标准灯光谱图以及对面积归一化后的光谱仪仪器函数 Figure 3 Spectrum of NeI lines and normalized IF I(x) |
通过拟合得出eCXRS的光谱仪仪器函数展宽半高全宽在11个像素点左右,将其视为多普勒展宽换算成离子温度,对应的温度将达到117.8 eV,若将其叠加到边界离子温度上,这对于边界离子温度诊断会是一个很大的影响,因此不能忽略仪器函数对原始光谱的卷积效应,需要对其进行反卷积处理。
1.2 实验算法贝叶斯条件概率公式为:
| $P({A}/{B}\;)=\frac{P({B}/{A}\;)P(A)}{P(B)}$ | (1) |
式中:P(A/B) 代表事件A在事件B条件下发生的可能性;P(A)、P(B) 代表事件A和事件B单独发生的可能性。
式 (1) 可改写为:
| $ P({{{T}_{i}}}/{{{A}_{k}}}\;)=\frac{P({{{A}_{k}}}/{{{T}_{i}}}\;)P({{T}_{i}})}{P({{A}_{k}})} $ |
式中:A代表所测量的数据;T代表真实的数据。
通过计算可以得出:
| ${{P}^{n+1}}({{T}_{i}})=\frac{1}{{{\alpha }_{i}}}{{P}^{n}}({{T}_{i}})\sum\limits_{k}{\frac{P({{{A}_{k}}}/{{{T}_{i}}}\;)P({{A}_{k}})}{\sum\limits_{j}{P({{{A}_{k}}}/{{{T}_{j}}}\;){{P}^{(n)}}({{T}_{j}})}}}$ | (2) |
式 (2) 为概率公式,其中P(Ti)、P(Ak)、ai、P(Ak/Ti) 同它们的测量可以通过矩阵方法表示为:
| $ \begin{align} & P({{T}_{i}})=\frac{{{T}_{i}}}{\sum\limits_{z}{{{T}_{z}}}}=\frac{{{T}_{i}}}{T} \\ & P({{A}_{k}})=\frac{{{A}_{k}}}{\sum\limits_{z}{{{A}_{z}}}}=\frac{{{A}_{k}}}{A} \\ & {{\alpha }_{i}}=\sum\limits_{k}{\frac{T}{A}{{R}_{ki}}=}\frac{T}{A}\sum\limits_{k}{I{{F}_{ki}}=}\frac{T}{A}{{\tau }_{i}} \\ & \sum\limits_{i}{P({{{A}_{k}}}/{{{T}_{i}}}\;)}P({{T}_{i}})=P({{A}_{k}})=\frac{{{A}_{k}}}{A}=\frac{\sum\limits_{i}{I{{F}_{ki}}{{T}_{i}}}}{A} \\ & =\sum\limits_{i}{\frac{T}{A}I{{F}_{ki}}\frac{{{T}_{i}}}{T}=}\sum\limits_{i}{\frac{T}{A}I{{F}_{ki}}P({{T}_{i}})} \\ \end{align} $ |
以上各式带入式 (2) 可得:
| $T_{i}^{n+1}=\frac{1}{{{\tau }_{i}}}T_{i}^{n}\sum\limits_{k}{\frac{I{{F}_{ki}}\cdot {{A}_{k}}}{\sum\limits_{j}{I{{F}_{kj}}\cdot T_{j}^{n}}}}$ | (3) |
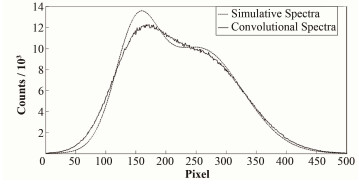
为了验证贝叶斯反卷积算法的可行性,首先进行仿真模拟。如图 4所示,模拟中包含的噪声为光子散粒噪声,由MATLAB产生标准正态分布伪随机数的函数产生,卷积公式为:
|
图 4 仿真原始光谱以及卷积后光谱 Figure 4 Spectra comparison before and after convolution |
| $ y\left( x \right)=o\left( x \right)\otimes \text{IF}\left( x \right)+n\left( x \right) $ |
式中:y(x) 代表卷积后光谱;o(x) 代表模拟的原始光谱;IF (x) 代表仪器函数;n(x) 代表光子散粒噪声。图 4中虚线代表模拟的原始光谱,实线为卷积后的光谱。
下面通过贝叶斯反卷积算法、已知的仿真y(x) 和IF (x) 反卷积出o(x),同时采用Savitzky-Golay算法进行平滑处理,通过模拟仿真来验证贝叶斯反卷积算法的可行性。
反卷积结果如图 5所示,实线代表包含噪声的原始光谱,虚线则代表贝叶斯反卷积随着迭代次数反卷积后的光谱。可以看出,在迭代次数不高时,如图 5(a-c)所示,随着迭代次数增加,反卷积后的光谱逐渐趋近于原始光谱。但是随着迭代再次增加,如图 5(d-f)所示,在迭代次数增加到50、100、500次,发现反卷积后的光谱反而偏离真实谱线,如图 5(d-f)中箭头所示,在此部分区域发生明显的光谱变形。因此需要对贝叶斯反卷积迭代次数进行估计。
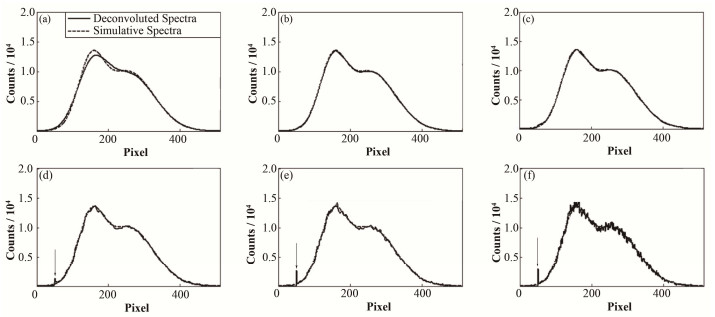
|
图 5 反卷积过程中光谱变化 (a) 迭代1次,(b) 迭代10次,(c) 迭代20次,(d) 迭代50次,(e) 迭代100次,(f) 迭代500次 Figure 5 Change of spectra during iteration. (a) Iteration number 1, (b) Iteration number 10, (c) Iteration number 20, (d) Iteration number 50, (e) Iteration number 100, (f) Iteration number 500 |
采用误差平方和 (Squares Sum of Estimation, SSE) 来判定最佳迭代次数,SSE的判定公式为:
| $ SSE=\sum\limits_{x}{{{[{{T}^{N}}(x)-o(x)]}^{2}}} $ |
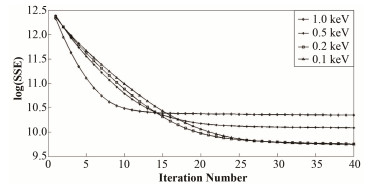
式中:TN(x) 表示第N次迭代后的反卷积谱线;o(x) 对全局域(模拟中为像素点1-512)作log (SSE) 来判定合理的迭代次数。同时模拟实验中离子温度为1 keV、0.5 keV、0.2 keV以及0.1 keV的情况,所对应的半高全宽分别为32.01、22.63、14.31、10.12像素点来判断迭代次数是否会有相应的变化,所得结果如图 6所示。可以看出,随着迭代次数的增加误差会减小,但是并不是每个离子温度所需要的迭代次数都相同,会呈现离子温度越低所需要迭代次数越高才能到达较理想的效果,例如离子温度在1keV时迭代次数在10左右就会达到理想反卷积结果,而离子温度在0.1 keV时则需要提高迭代次数至25左右才会达到理想的反卷积结果。因此具体的迭代次数的选择还需要考虑离子温度的大致情况来决定。
|
图 6 不同离子温度情况下随着迭代次数增加log (SSE) 的大小 Figure 6 Change of log (SSE) during iteration by different ion temperature |
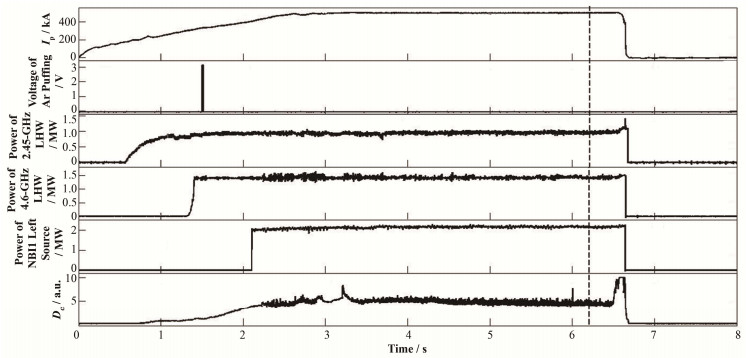
从仿真模拟结果可以看出,贝叶斯反卷积在合理的迭代次数下可以将谱线进行有效的还原,下面将此方法运用到实际的EAST实验中,验证此方法在实际操作中的可行性。选取EAST放电炮号为57116,基本放电参数如图 7所示,如等离子体电流平顶区为500 kA,图 7中信号名VJHPEV4表示在1.5 s充入氩气,同向中性束左源注入时间为2.1-6.6s,反卷积所选取时刻点为6.171 5 s,如图 7中竖直虚线所示,取自中性束注入时刻点。同时此炮除了包含有中性束注入外还存在2.45 GHz以及4.6 GHz低杂波 (Lower hybrid wave, LHW) 加热。
|
图 7 EAST 57116炮放电主要参数 Figure 7 Time traces of the main parameters for discharge (#57116) on EAST |
所选取观测道为eCXRS系统最外侧观测弦,其与同向中性束左源中心处交点由空间标定可知大半径为2 310 mm[19-20]。通过波长和CCD相机像素点对应关系[21],使用二次多项式拟合,得到:
| $y=(-3.2581\times {{10}^{-7}}){{x}^{2}}-0.01155x+530.7708$ | (4) |
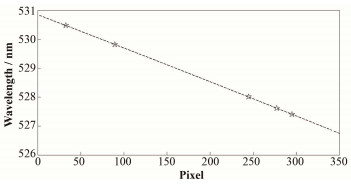
式中:x代表CCD上像素点位置;y为x像素点处对应的波长值。相应关系如图 8所示,图 8中五角形代表图 3中对应的5个不同波长的Ne Ⅰ线,同时拟合误差最大值为0.002 9 nm,大致为1/4个像素点,基本可以忽略。
|
图 8 波长和像素点对应关系 Figure 8 Corresponding relationship between wavelength and pixel |
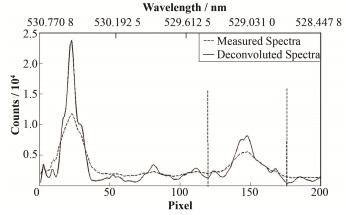
利用仪器函数(图 3)以及在CCD相机上测到的测量光谱,采用贝叶斯反卷积算法得到反卷积后的光谱。结果如图 9所示,虚线代表测量光谱,实线为经过贝叶斯反卷积后得到的光谱。通过对比可得,对测量光谱进行贝叶斯反卷积后,原本较宽的谱线变窄,同时原本被仪器函数卷积所淹没的多条谱线可以大致辨别,使得因为仪器函数卷积而变得较为困难的谱线识别工作初步得到解决。下面对作了反卷积后的光谱进行谱线分析,得到相应的杂质谱线波长以及种类。
|
图 9 6.171 5 s时第30通道经过贝叶斯反卷积后所得原始光谱以及测量光谱对比 Figure 9 Spectra comparison of the 30th channel before and after Bayesian deconvolution at 6.171 5 s |
根据波长标定所得结果可知529.059 nm对应像素点位置在147像素点左右,因此可以选取如图 9中竖直虚线中间区域,即像素点范围为120-180(波长范围为528.710 9-529.405 7 nm),进行谱线分析。
图 10为在120-180像素点范围内对反卷积后的光谱进行高斯拟合所得结果。由于所选取的是最外侧观测弦,靠近等离子体边界,中性束注入条件下,CVI主动谱线和被动谱线得到的离子旋转速度近似相等,谱线的多普勒频移可以忽略,因此在529.059 nm附近CVI谱线可以使用单高斯拟合。
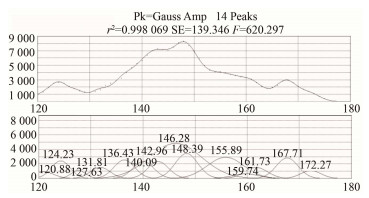
|
图 10 120-180像素点第30通道中性束注入时刻光谱反卷积拟合结果 Figure 10 Results of fitting spectra of the 30th channel between the pixels of 120 to 180 by deconvolution with NBI |
利用原子数据库[22]结合马克内环境以及精确的波长标定结果,我们对测量到的杂质谱线进行了细致的谱线识别。得到的主要杂质及其谱线如表 1所示,谱线识别的结果可以利用EAST上的快速极紫外 (Extreme ultraviolet, EUV) 谱仪[23]对芯部杂质的监测来加以验证。如图 11所示,芯部杂质监测显示在中性束注入时刻 (6.171 5 s) 出现了多种杂质的出现,包括铁、铜等金属杂质,边界CXRS系统的观测视线部分观测到了EAST位于B窗口的离子回旋加热 (Ion cyclotron resonance heating, ICRF) 天线上,ICRF天线材质为不锈钢外面镀铜,可以验证前文所判断的杂质种类包含铁、铜等杂质成立。
| 表 1 eCXRS系统中性束注入时刻通道30反卷积杂质分析 Table 1 Result of impurity analysis of the 30th channel by deconvolution with NBI |
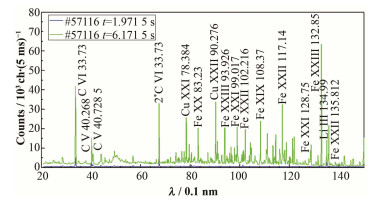
|
图 11 57116炮不同时刻杂质对比 Figure 11 Impurity analysis of EAST #57116 from EUV |
边界处Fe Ⅰ、Fe Ⅱ谱线的判断如图 12所示,图 12(a)为低价态的铁离子密度随着径向长度占此杂质总浓度的百分比变化,由等离子体的电子温度、密度分布以及输运过程决定;图 12(b)选取的通道分别为25通道 (ρ=0.994 88)、30通道 (ρ=1.046 61),观测视线都穿过等离子体到边界,通道25相对通道30更加靠近芯部。通过对比可以看出,第25通道在相同时刻下,低价态铁杂质区域的谱线明显比第30通道谱线要弱,同图 12(a)的趋势一致,证明前文所判断的低价态的铁杂质谱线成立。
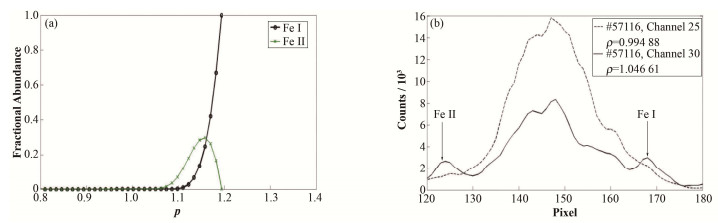
|
图 12 铁各个价态的离子密度随径向长度占此杂质总浓度的百分比变化 (a) 和57116炮6.171 5 s时不同通道光谱对比 (b) Figure 12 Fractional abundance of Fe impurity (a) and compare with spectra between different channels at 6.171 5 s (b) |
为了验证CVI (529.059 nm,n=8→7) 谱线附近存在氩杂质谱线,选充氩气以及不充氩气的两炮对比来判别。对比结果如图 13(a)所示,选取的两炮分别为61043以及61044,其中61043炮未向真空室内充入氩气,61044炮则充入较多氩气,选取通道皆为最外侧观测弦,通过对比两炮反卷积后的光谱可以得出,两者光谱中部分像素点区域有明显的差异,61044炮比61043炮在这部分区域谱线明显增强。通过对比EUV探测氩杂质[24]的结果,如图 13(b)所示,可以看到主要为氩杂质谱线,同时其他杂质谱线并不明显,验证了前文猜测。确认了这几条明显变化的谱线为Ar Ⅱ线后,对图 13(a)中61044炮0-230像素点中的谱线进行高斯拟合,所得结果如表 2所示,表 2中的下划线部分Ar Ⅱ波长在考虑到波长拟合误差以及实验外部条件变化后可以和表 1中所判断的Ar Ⅱ波长对应,因此可以得出在CXRS诊断CVI (529.059 nm,n=8→7) 波长附近有这些Ar Ⅱ杂质谱线的影响。
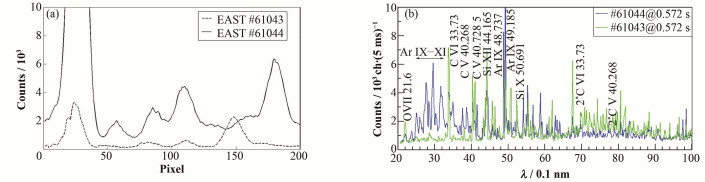
|
图 13 61043(未充氩)炮同61044(充氩)炮光谱 (a) 和EUV杂质诊断 (b) 对比 Figure 13 Comparison with the result of spectra (a) and EUV data (b) before and after Ar puffing |
| 表 2 eCXRS系统61044(充氩)炮杂质分析 Table 2 Result of impurity analysis of the shot #61044 with Ar puffing |
仪器函数的卷积效应会影响电荷交换复合光谱诊断的离子温度诊断精度,需要利用反卷积算法来扣除仪器函数的卷积效应。通过反卷积,可以使原本被仪器函数卷积的谱线变窄,谱线拟合后的半高全宽精度提高,使得离子温度的诊断精度提高。本文从模拟仿真和实验两个方面验证了使用贝叶斯方法可以有效扣除仪器函数的卷积影响。在EAST实验中,通过贝叶斯反卷积,可以使得原本被仪器函数卷积的各条谱线大致分辨出来,与EUV诊断数据相结合,可以判断出所测量谱线旁边的干扰杂质谱线种类以及波长。在扣除了这些谱线后,可使得CVI谱线拟合更加精确。
致谢 感谢NBI课题组为CXRS诊断系统的运行提供了基础,同时感谢杂质诊断组提供了放电过程中杂质分布信息。| [1] | Isler R C. Observation of reaction H0+O8→H+(O7+) during neutral-beam injection into ormak[J]. Physical Review Letters, 1977, 38(23): 1359–1362. DOI: 10.1103/PhysRevLett.38.1359 |
| [2] | Shi Y J, Fu J, Li Y Y, et al. Charge exchange recombination spectroscopy based on diagnostic neutral beam in the HT-7 tokamak[J]. Plasma Science and Technology, 2010, 12: 11–14. DOI: 10.1088/1009-0630/12/1/03 |
| [3] | Li Y Y, Fu J, Lyu B, et al. Development of the charge exchange recombination spectroscopy and the beam emission spectroscopy on the EAST tokamak[J]. Review of Scientific Instruments, 2014, 85(11): E428. DOI: 10.1063/1.4890408 |
| [4] | Han X Y, Duan X R, Yang L M, et al. First charge exchange recombination spectroscopy diagnostic in HL-2A tokamak[J]. Chinese Physics Letters, 2010, 27(5): 055202. DOI: 10.1088/0256-307x/27/5/055202 |
| [5] | Andrew Y, Hawkes N C, Crombe K, et al. Improved charge exchange spectroscopy on the Joint European Torus for ion temperature and rotation velocity profiles[J]. Review of Scientific Instruments, 2006, 77(10): E913. DOI: 10.1063/1.2228810 |
| [6] | Koide Y, Sakasai A, Sakamoto Y, et al. Multichordal charge exchange recombination spectroscopy on the JT-60U tokamak[J]. Review of Scientific Instruments, 2001, 72(1): 119–127. DOI: 10.1063/1.1332115 |
| [7] | Fonck R J, Goldston R J, Kaita R, et al. Plasma ion temperature measurements via charge exchange recombination radiation[J]. Applied Physics Letters, 1983, 42(3): 239–241. DOI: 10.1063/1.93893 |
| [8] | Jia J Y.Single image motion deblurring using transparency[C].Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 2007:1-8. |
| [9] | Shan Q, Jia J Y, Agarwala A. High-quality motion deblurring from a single image[J]. ACM Transactions on Graphics, 2008, 27(3): 1–10. DOI: 10.1145/1360612.1360672 |
| [10] | Gold R.An iterative unfolding method for response matrices[M].Argonne National Laboratory, 1964.DOI:10.2172/4634295. |
| [11] | Kundur D, Hatzinakos D. Blind image deconvolution[J]. IEEE Signal Processing Magazine, 1996, 13(3): 43–64. DOI: 10.1109/79.489268 |
| [12] | Yap K H, Guan L, Liu W, et al. A recursive soft-decision approach to blind image deconvolution[J]. IEEE Transaction on Signal Processing, 2003, 51(2): 515–526. DOI: 10.1109/TSP.2002.806985 |
| [13] | Sievers P, Weber T, Miche T, et al. Bayesian deconvolution as a method for the spectroscopy of X-rays with highly pixelated photon counting detectors[J]. Journal of Instrumentation, 2012, 7: 1–19. DOI: 10.1088/1748-0221/7/03/P03003 |
| [14] | Kennett T J, Prestwich W V, Robertson A, et al. Bayesian deconvolution Ⅰ:convergence properties[J]. Nuclear Instruments and Methods in Physics Research A, 1978, 151: 285–292. DOI: 10.1016/0029-554X(78)90502-5 |
| [15] | Armstrong N, Hibbert D B. An introduction to Bayesian methods for analyzing chemistry data Part 1:an introduction to Bayesian theory and methods[J]. Chemometrics and Intelligent Laboratory Systems, 2009, 97: 194–210. DOI: 10.1016/j.chemolab.2009.04.001 |
| [16] | Wan Y X, Li J G, Weng P D, et al. First engineering commissioning of EAST tokamak[J]. Plasma Science and Technology, 2006, 8: 253–254. DOI: 10.1088/1009-0630/8/3/01 |
| [17] | Wu B, Wang J, Li J, et al. Neutral beam injection simulation of EAST[J]. Fusion Engineering and Design, 2011, 86: 947–950. DOI: 10.1016/j.fusengdes.2011.01.148 |
| [18] | Ida K, Sakamoto Y, Yoshinuma M, et al. Measurement of derivative of ion temperature using high spatial resolution charge exchange spectroscopy with space modulation optics[J]. Review of Scientific Instruments, 2008, 79: 053506. DOI: 10.1063/1.2921702 |
| [19] |
冯双园, 李颖颖, 余奕, 等. EAST托卡马克上截面效应对电荷交换复合光谱测量结果的影响[J].
核技术, 2016, 39(4): 040602.
FENG Shuangyuan, LI Yingying, YU Yi, et al. Cross-section effect on charge exchange recombination spectroscopy measurement with the EAST tokamak[J]. Nuclear Techniques, 2016, 39(4): 040602. DOI: 10.11889/j.0253-3219.2016.hjs.39.040602 |
| [20] |
张镱, 李颖颖, 符佳, 等. EAST托卡马克电荷交换复合光谱诊断的绝对强度标定[J].
核技术, 2015, 38(7): 070603.
ZHANG Yi, LI Yingying, FU Jia, et al. Absolute intensity calibration of the charge exchange recombination spectroscopy system on EAST[J]. Nuclear Techniques, 2015, 38(7): 070603. DOI: 10.11889/j.0253-3219.2015.hjs.38.070603 |
| [21] |
尹相辉, 李颖颖, 符佳, 等. EAST上电荷交换复合光谱诊断波长标定研究[J].
光学学报, 2016, 36(6): 063002.
YIN Xianghui, LI Yingying, FU Jia, et al. Wavelength calibration of charge exchange recombination spectroscopic diagnostic system on EAST[J]. Acta Optica Sinica, 2016, 36(6): 063002. DOI: 10.3788/AOS201636.0630002 |
| [22] | Bautista M A, Kallman T R. The XSTAR atomic database[J]. The Astrophysical Journal Supplement Series, 2001, 134(1): 139–149. DOI: 10.1086/320363 |
| [23] | Zhang L, Morita S, Xu Z, et al. A fast-time-response extreme ultraviolet spectrometer for measurement of impurity line emissions in the experimental advanced superconducting tokamak[J]. Review of Scientific Instruments, 2015, 86: 123509. DOI: 10.1063/1.4937723 |
| [24] |
张鹏飞, 张凌, 许棕, 等. 极紫外波段Ar光谱分析在EAST偏绿器杂质屏蔽效应研究中的应用[J].
光谱学与光谱分析, 2016, 36(7): 2134–2138.
Pengfei, ZHANG Ling, XU Zong, et al. Application of extreme-ultraviolet Ar spectra analysis in the study of divertor impurity screening in EAST tokamak[J]. Spectroscopy and Spectral Analysis, 2016, 36(7): 2134–2138. DOI: 10.3964/j.issn.1000-0593(2016)07-2134-05 |


