2. 中国工程物理研究院 核物理与化学研究所 绵阳 621900;
3. 西南科技大学 核废物与环境安全国防重点学科实验室 绵阳 621010;
4. 成都理工大学 地质灾害防治与地质环境保护国家重点实验室 成都 610059
2. Institute of Nuclear Physics and Chemistry, China Academy of Engineering Physics, Mianyang 621900, China;
3. Fundamental Science on Nuclear Wastes and Environmental Safety Laboratory, Southwest University of Science and Technology, Mianyang 621010, China;
4. State Key Laboratory of Geohazard Prevention and Geoenvironment Protection, Chengdu University of Technology, Chengdu 610059, China
随着核科学技术的发展,γ射线测量技术已经广泛应用到核检测、核退役、核医学、地质、食品等诸多领域[1-3]。在桶装核废物样品无损检测分析过程中,需要对大型样品进行透射测量,从而获得线衰减系数,对样品进行自吸收校正,从而获得样品活度,常用方法为分层γ扫描技术[4]。由于样品体积比较大,在实验透射测量过程中,需要透射源强度较大,且同时要求发射的γ射线能量较广,才能获得样品对于不同能量γ射线的线衰减系数[5]。在实验室条件下,往往受到放射源强度和射线能量不足的限制,在中低密度范围内,γ射线的线衰减系数主要与入射γ射线能量、待测样品介质密度和成分相关,科研人员提出了采用平均密度法进行线衰减系数的确定[6-7]。
由于蒙特卡罗方法具有节约成本、快捷方便、能够很好地解决数值计算问题等优点[8],本文针对桶装核废物样品检测中,确定γ射线衰减系数的问题,采用蒙特卡罗程序对多种不同能量γ射线在不同密度样品中的线衰减系数进行了模拟计算,采用较为通用的函数模型进行多元非线性回归得到函数参数。所得函数确定的γ射线衰减系数值与实验测量值进行比较,并对两者的误差加以分析讨论,从而验证该方法所得函数的准确性。
1 原理根据Beer-Lambert定律[9],具有一定能量和强度的平行入射γ射线束,穿过一定厚度的均匀密度材料,γ射线的衰减规律如式 (1) 所示:
| $I(E,\rho ) = {I_0}(E,\rho ) \cdot \exp [ - \mu (E,\rho ) \cdot x(\rho )]$ | (1) |
式中:E为γ射线能量;ρ为材料密度;x(ρ) 为材料厚度;μ(E, ρ) 为线衰减系数;I0(E, ρ) 和I(E, ρ) 分别为衰减前后的γ射线强度。在实验测量和计算过程中,我们得到的是γ射线特征峰计数,因此,式 (1) 转变为式 (2):
| $N(E,\rho )={{N}_{0}}(E,\rho )\cdot \exp [-\mu (E,\rho )\cdot x(\rho )]$ | (2) |
式中:N0(E, ρ) 和N(E, ρ) 分别为衰减前后在γ能谱中特征峰的计数。γ射线在材料中的线衰减系数计算如式 (3) 所示:
| $\mu (E,\rho ) = - \frac{1}{{x(\rho )}}{\text{In}}[\frac{{N(E,\rho )}}{{{N_0}(E,\rho )}}]$ | (3) |
可以看出,μ(E, ρ) 与E和ρ有直接关系,我们采用的函数模型如式 (4) 所示:
| $\begin{gathered} \mu (E,\rho ,{a_i}) = \exp [{a_1} + {a_2}{\text{In}}(E) + {a_3}\rho + \\ _{}^{}{a_4}{\text{I}}{{\text{n}}^2}(E) + {a_5}{\text{In}}(\rho ){\text{In}}(E) + {a_6}{\rho ^{1/5}}] \\ \end{gathered} $ | (4) |
式中:ai(i=1, 2, …, 6) 为待定参数。式 (4) 为不同能量γ射线在不同密度样品中的线衰减系数值,经过选取线衰减系数、样品密度、γ射线能量,采取逐步多次拟合方法,由最小拟合误差得到最优的拟合公式。通过实验测量或模拟计算,得到多个不同入射γ射线能量和不同密度样品条件下的线衰减系数,对线衰减系数进行多元非线性回归,即可得到函数参数。
2 实验测量 2.1 实验材料核设施退役产生的放射性废物主要包括大量的混凝土碎块和低污染金属,核废物处理厂对放射性废物进行处理的过程中,通常对中低放核废物采取沥青固化、水泥固化、塑料固化,对高放液体废物采取玻璃固化[10-11]。参考国内外其他研究人员所采用的桶装核废物样品填充材料,实验采用6种样品材料:水、聚乙烯块、塑料块、玻璃碎块、混凝土块、铝块,其密度如表 1所示。
| 表 1 材料参数 Table 1 Parameters of materials |
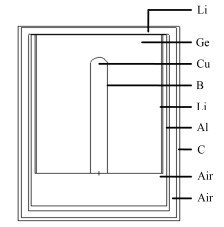
实验采用的γ探测器为美国ORTEC公司生产的电制冷P型同轴HPGe探测器,其结构见图 1。
|
图 1 HPGe探测器结构 Figure 1 Geometry of the HPGe detector |
探测器晶体直径70 mm,长度82.6 mm,冷指半径9 mm,长度69 mm,前端死层厚度小于0.015mm,侧边死层厚度0.7 mm,内死层厚度0.3μm,前端Al层厚度0.03 mm,侧边Al层厚度1.5 mm,前端碳纤维外壳厚度0.9 mm,侧边碳纤维外壳厚度1.6 mm。探测器偏压2600 V,能量响应范围0.004-10 MeV。
2.3 γ源实验采用的标准γ放射源:1) 137Cs活度为3.286×105Bq,661.661 keV射线强度为85%;2) 60Co活度为1.877×105 Bq,1173.238 keV射线绝对强度为99.87%,1332.513 keV射线强度为99.982%。
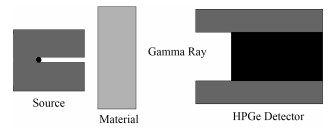
实验测量如图 2所示。将γ源置于透射源准直孔内,表 1所列材料置于样品位置,采用HPGe探测器对置入样品前后的γ能谱进行测量,每个实验条件下测三次,每次测500 s,取平均值作为能谱数据,由式 (3) 计算得到γ射线的线衰减系数实验值,如表 2所示。
|
图 2 线衰减系数实验测量 Figure 2 Experimental measurement of linear attenuation coefficient |
| 表 2 线衰减系数实验值 Table 2 Experimental results of linear attenuation coefficient |
桶装核废物样品的介质密度一般小于3.0g·cm-3,桶内核素发射γ射线能量范围一般在1.5MeV以内。模拟计算采用的4个系列样品及元素质量分数比例为:1号系列样品成分:C (85.71%)、H (14.29%);2号系列样品成分:H (11.11%)、O (88.89%);3号系列样品成分:H (14.81%)、O (56.25%)、Mg (0.71%)、Al (1.11%)、Si (22.21%)、S (0.35%)、Ca (3.25%)、Fe (1.31%);4号系列样品成分:Si (34.21%)、Al (2.647%)、Fe (1.05%)、Ca (0.571%)、Mg (0.18%)、K (1.417%)、P (0.086%)、O (50.829%)、H (9.01%)。4个系列样品的厚度均为10 cm,密度范围取值为0.3-3.0 g·cm-3,每0.3 g·cm-3为一间隔,总共计算10个点。入射γ射线的能量范围取值为100-1500keV,每100 keV为一间隔,总共计算15个点。根据图 2建立MCNP模型,在所取γ射线能量和样品密度范围内,可计算得到线衰减系数的变化规律。模拟采用单能、窄束γ光子,垂直入射到样品材料上,模拟计算时认为探测器系统对光子的探测效率达到理想状态,每次计算的粒子总数为107,最终的蒙特卡罗模拟计算结果归一化到一个源粒子上。
3.2 模拟结果通过MCNP程序的模拟,结合式 (3) 计算,得到不同能量γ射线在不同密度样品中的线衰减系数值,如表 3所示。
| 表 3 1-4号系列样品线衰减系数模拟结果 Table 3 Simulations of linear attenuation coefficient for 1-4# series samples |
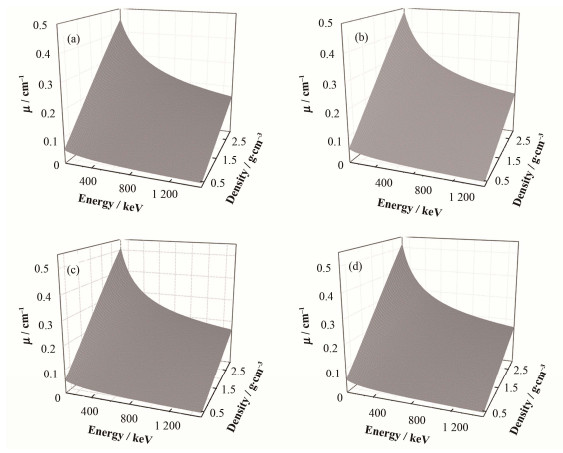
结合表 3中4个系列样品中γ射线衰减系数的模拟值,以式 (4) 为函数模型进行多元非线性回归,得到待定参数ai(i=1, 2, …, 6),如表 4所示,从而得到γ射线衰减系数函数及参数,其三维效果如图 3所示。
| 表 4 线衰减系数函数参数拟合结果 Table 4 Parameters of linear attenuation coefficient function |
|
图 3 不同样品中γ射线的线衰减系数函数分布 (a) 1#,(b) 2#,(c) 3#,(d) 4# Figure 3 Function description of linear attenuation coefficients for different series samples. (a) 1#, (b) 2#, (c) 3#, (d) 4# |
从图 3可以看出,模拟计算结果表明,入射γ射线相同能量下,样品密度越大,线衰减系数值越大,且呈线性增长变化规律。样品相同密度下,入射γ射线能量越大,线衰减系数值越小,且呈指数减小变化规律。对于不同样品基质成分,密度和入射γ射线相同能量的情况下,线衰减系数值有一定差异。
3.4 误差分析为了验证所得到的γ射线衰减系数函数准确性,取实验测量时的样品密度和入射γ射线能量,带入上述的4个不同参数函数,将得到的函数值与实验值进行比较,计算二者的相对误差δ:
| $\delta = \left[ {\left( {{\mu _F} - {\mu _E}} \right)/{\mu _E}} \right] \times 100\% $ | (5) |
误差结果如表 5所示。其中X为661.661 keV,Y为1173.238 keV,Z为1332.523 keV。
| 表 5 模拟值与实验值误差 Table 5 Relative deviation between the experimental and simulation results (%) |
由表 5可以看出,当样品密度较低时,误差值均在4%以内,随着样品密度增加,误差值有所增大,总体而言,所得函数值与实验值的相对误差均在7%以内,选择不同的拟合公式模型,所得线衰减系数值的计算结果存在一定扰动,必然会影响计算结果与实验值之间的误差。总体说明蒙特卡罗计算所得函数值与实验测量值较为吻合,所采用的函数模型正确表示γ射线的线衰减系数随γ射线能量和样品密度变化的关系特征,进而验证γ射线的线衰减系数主要由γ射线能量和样品密度决定。
4 结语通过蒙特卡罗程序计算了多种不同能量γ射线在不同密度样品中的线衰减系数,且模拟值与实验值较为符合。对线衰减系数进行多元非线性回归,确定了线衰减系数函数及参数,得到了γ射线能量、样品密度与线衰减系数的关系特征。证明了蒙特卡罗方法确定γ射线线衰减系数的实用性,特别是在实验条件不足的情况下,该方法所得具体函数值具有重要的参考价值。该方法不仅可以用于桶装核废物样品检测分析中的线衰减系数确定,还可应用在辐射防护屏蔽材料的研究中,同样具有重要意义。
| [1] |
张金钊.核废物桶层析γ扫描关键技术硏究[D].成都:成都理工大学, 2014.
ZHANG Jinzhao.Research on key technologies of nuclear waste drum tomographic gamma scanning[D].Chengdu:Chengdu University of Technology, 2014. |
| [2] |
张海青, 倪邦发, 田伟之, 等. HPGe探测器点源效率与其空间位置的函数关系[J].
核技术, 2010, 33(11): 839–843.
ZHANG Haiqing, NI Bangfa, TIAN Weizhi, et al. The determination of functional relationship between point source efficiency and its space position for an HPGe detector[J]. Nuclear Techniques, 2010, 33(11): 839–843. |
| [3] |
郑洪龙, 庹先国, 石睿, 等. 蒙特卡罗模拟确定HPGe探测器点源效率函数及参数[J].
核技术, 2015, 38(4): 040201.
ZHENG Honglong, TUO Xianguo, SHI Rui, et al. Monte Carlo simulations of efficiency function of HPGe detector to point sources and determination of its parameters[J]. Nuclear Techniques, 2015, 38(4): 040201. DOI: 10.11889/j.0253-3219.2015.hjs.38.040201 |
| [4] |
王仲奇, 宗波, 郜强, 等. 分层γ扫描定量分析中层内放射性非均匀分布影响分析[J].
原子能科学技术, 2012, 46(1): 103–108.
WANG Zhongqi, ZONG Bo, HAO Qiang, et al. Study on effect of radial-heterogeneity in segmented gamma scanning analysis[J]. Atomic Energy Science and Technology, 2012, 46(1): 103–108. |
| [5] |
翁文庆, 王德忠, 张勇, 等. 用多个能量探测方法校正层析γ扫描透射图像重建中射线线衰减系数[J].
辐射防护, 2008, 28(1): 24–28.
WENG Wenqing, WANG Dezhong, ZHANG Yong, et al. The method of multi-energy gamma rays to rectify linear attenuation coefficient in image reconstruction of tomographic gamma scanning[J]. Radiation Protection, 2008, 28(1): 24–28. |
| [6] |
刘诚.中低放射性废物改进型γ扫描技术及活度重建算法研究[D].上海:上海交通大学, 2013.
LIU Cheng.Study on the improved gamma scanning technique and activity reconstruction method for low and intermediate level radioactive waste[D].Shanghai:Shanghai Jiao Tong University, 2013. |
| [7] | Gillespie B, Zebarth M.Comparison of a variety of gamma attenuation correction techniques for different waste matrices[C].14th Annual Symposium on Safeguards and Nuclear Management, Salamanca, Spain, 1992. |
| [8] |
许淑艳.
蒙特卡罗方法在实验核物理中的应用[M]. 北京: 原子能出版社, 2006: 267-269.
XU Shuyan. Application of Monte Carlo method in nuclear physics experiment[M]. Beijing: Atomic Energy Press, 2006: 267-269. |
| [9] | Parnis J M, Oldham K B. Beyond the Beer-Lambert law:the dependence of absorbance on time in photochemistry[J]. Journal of Photochemistry and Photobiology A:Chemistry, 2013, 267: 6–10. DOI: 10.1016/j.jphotochem.2013.06.006 |
| [10] |
罗上庚.放射性废物处理与处置[M].北京:中国环境科学出版社, 2007:35-44, 103-116.
LUO Shanggeng.Treatment and disposal of radioactive waste[M].Beijing:China Environmental Science Press, 2007:35-44, 103-116. |
| [11] |
王效忠, 隋洪志, 刘功发, 等. 200 L桶装α废物检测装置的研制[J].
原子能科学技术, 2002, 36(1): 5–9.
WANG Xiaozhong, SUI Hongzhi, LIU Gongfa, et al. Development of a passive-active shuffler for 200 L drum[J]. Atomic Energy Science and Technology, 2002, 36(1): 5–9. |


