2. 中国科学院过程工程研究所 多相复杂系统国家重点实验室 北京 100190;
3. 西安交通大学 核能科学与技术学院 西安 710049
2. State Key Laboratory of Multiphase Complex Systems, Institute of Process Engineering, Chinese Academy of Sciences, Beijing 100190, China;
3. School of Nuclear Science and Technology, Xi'an Jiaotong University, Xi'an 710049, China
固态燃料熔盐堆堆芯是由石墨球随机堆积而成的,在分析中建立随机堆积的小球模型存在较大困难和不确定性。因此,为了便于计算,通常选择规则小球排布方式进行建模。李华等[1]采用体心立方排布方式对球床式水冷堆堆芯进行了建模,并对冷却剂热工水力特性进行了初步的研究。李健等[2]研究了正三角形排列方式和体心立方排列方式下球床堆单相阻力流动特性,并将模拟结果与试验结果进行了对比。潘登等[3]利用ANSYS FLUENT 14.5软件对面心立方排列球床进行了建模,得到了球床压降、对流换热Nu随球床内流动Re变化的曲线,拟合了修正Nu公式,并将该公式应用于3 cm直径规则球床中。Song等[4]采用计算流体力学(Computational Fluid Dynamics, CFD)分析方法研究了面心立方(Face Centered Cubic, FCC)和体心立方(Body Centered Cubic, BCC)排布方式下堆芯压降和Nu的变化。目前,国内外针对固态熔盐堆堆芯流动和换热进行研究的公开文献还很少。
本文使用ANSYS FLUENT 15.0软件进行固态燃料熔盐堆堆芯的局部建模和分析计算,研究FCC和BCC排布方式下10 MW固态燃料熔盐堆堆芯流动和换热的特性,为固态钍基熔盐堆(Thorium Molten Salt Reactor-Solid Fuel, TMSR-SF)的设计和安全分析提供支持。
1 TMSR-SF介绍TMSR-SF堆芯热功率为10 MW,活性区为圆柱形固定球床堆芯,一次装料11043颗燃料元件,燃料元件为全陶瓷包覆颗粒球形燃料元件,燃料球直径为6.0 cm,堆芯活性区体积1.95 m3,堆内包括16根控制棒、一个中子源通道和三个实验测量通道[5]。反应堆一回路熔盐为FliBe (LiF-BeF2),二回路熔盐为FliNaK (LiF-NaF-KF)。一回路熔盐堆芯进口温度为600 ℃,出口温度为628 ℃,质量流速为41.3kg·s-1[6-9]。
2 模型建立和边界条件 2.1 几何建模与网格划分为保证建模区域的高度一致,FCC排布下模拟区域有5层小球(包括3个完整小球、8个半球和12个1/4球),BCC排布下模拟区域有7层小球(包括3个完整小球、16个1/4球)。为保证流动下游不出现回流,上游流场充分发展,几何模型在上下游各延伸一段长方体几何。每个小球都是由厚度为1 cm的石墨壳和直径为5 cm的石墨基体组成。
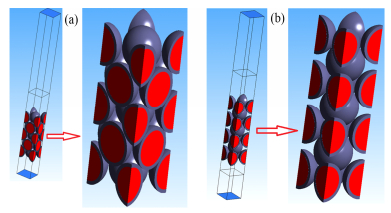
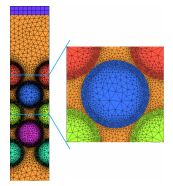
图 1是FCC和BCC的三维几何图。图 2是FCC排布下的整体和局部网格划分,球床区域采用四面体网格,并在小球表面和球间接触点附近进行加密处理,延伸段划分六面体网格。小球表面的y+控制在1-20,接触点处y+小于5,以保证加强壁面函数的适用性。BCC的网格划分方式与FCC类似。
|
图 1 FCC (a)和BCC (b)的三维几何图 Figure 1 3D geometry of the FCC (a) and BCC (b). |
|
图 2 FCC排布的网格划分 Figure 2 Schematic grid of the FCC arrangement mode. |
表 1为FCC排布下网格无关性分析结果,经无关性验证,当网格数量达到5796447时,关键参数的计算值相差不到0.5%,因此本文在FCC排布分析时用的网格数量为5796447。
| 表 1 FCC排布下网格无关性验证数据 Table 1 Data of grid-independent verification for FCC arrangement mode. |
表 2为BCC排布下网格无关性分析结果,经无关性验证,当网格数量达到5446239时,各关键参数的计算值相差不到0.5%,因此本文在BCC排布分析时用的网格数量为5446239。
| 表 2 BCC排布下网格无关性验证数据 Table 2 Data of grid-independent verification for BCC arrangement mode. |
湍流模型选择的是重整化群(Re-Normalization Group, RNG) k-ε模型。
| $\rho \frac{{Dk}}{{Dt}} = \frac{\partial }{{\partial {x_i}}}\left[{\left( {{\alpha _k}{\mu _{{\text{eff}}}}} \right)\frac{{\partial k}}{{\partial {x_i}}}} \right] + {G_k} + {G_b} - \rho \varepsilon - {Y_M} + {S_k}$ | (1) |
| $\begin{gathered} \rho \frac{{D\varepsilon }}{{Dt}} = \frac{\partial }{{\partial {x_i}}}\left[{\left( {{\alpha _\varepsilon }{\mu _{{\text{eff}}}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_i}}}} \right] + {C_{1\varepsilon }}\frac{\varepsilon }{k}({G_k} + {C_{3\varepsilon }}{G_b}) - \\ _{}{C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k} - R + {S_\varepsilon } \\ \end{gathered} $ | (2) |
式中:Gk为由于平均速度梯度引起的湍动能;Gb为由于浮升力引起的湍动能;YM为可压湍流的脉动膨胀对总耗散率的贡献;常数C1ε=1.42,C2ε=1.68;Sk和Sε是用户自定义源项;αk和αε分别是湍动能k和耗散率ε的有效湍流普朗特数的倒数,可用式(3)计算:
| ${\left| {\frac{{\alpha - {{1.392}_{}}9}}{{{\alpha _0} - {{1.392}_{}}9}}} \right|^{{{0.632}_{}}1}}{\left| {\frac{{\alpha + {{2.392}_{}}9}}{{{\alpha _0} + {{2.392}_{}}9}}} \right|^{{{0.367}_{}}9}} = \frac{{{\mu _{{\text{mol}}}}}}{{{\mu _{{\text{eff}}}}}}$ | (3) |
式中:α0=1.0,在高雷诺数时,αk=αε≈1.393。
湍流粘性系数计算公式为:
| ${\text{d}}\left( {\frac{{{\rho ^2}k}}{{\sqrt {\varepsilon \mu } }}} \right) = 1.72\frac{{\tilde \nu }}{{\sqrt {{{\tilde \nu }^3} - 1 - C\nu } }}{\text{d}}\tilde \nu $ | (4) |
式中:Cν≈100。
2.3 边界条件和计算工况液态熔盐从底部向上流过球床,进口采用已知速度和温度边界条件,出口采用压力边界出口,并假定表压为零。石墨球分为石墨壳和均匀石墨基体两个区,两区采用各自的物性参数(均假设为常数),由于石墨基体内部均匀分散着TRISO (Tristructural isotropic)燃料颗粒,故假设其体积功率均匀分布。另外,液态熔盐和小球表面之间采用加强壁面函数进行近壁面处理。表 3给出了熔盐物性和计算的初始参数[10]。
| 表 3 熔盐物性和计算参数 Table 3 Properties of molten salts and calculation parameters. |
图 3给出了两种排布方式下的整体流线分布。熔盐通过球间间隙时速度增大,沿着球面向下游流动直到发生分离流,分离流冲击下一排小球后形成回流,于是在较大的孔隙里产生漩涡。FCC排布下的流线呈现出周期性弯曲,流体与大部分球面能充分接触。而BCC排布下的流线大体呈直线,小球仅在局部区域与流体充分接触,小球底部和顶部的流体几乎呈静止状态。

|
图 3 FCC (a)和BCC (b)的整体流线图 Figure 3 Streamline distributions of the general flow for the FCC (a) and BCC (b). |
图 4是两种排布结构下所截取的两个横截面处的速度矢量分布。可以看到小球流经窄缝时速度显著增加,通过窄缝后在下游形成二次流。对比图 4(a)、(b)可以发现,不管采用哪种小球排布方式,4个小球围成的平面间隙内都会产生4对二次流。但FCC排布由于6个小球相互接触,围成的间隙体积更小,形成的二次流尺度明显小于BCC排布的二次流尺度。FCC排布形成的间隙内速度矢量分布较为均匀,有利于均匀排出周围小球的热量;而BCC排布下间隙最中间区域的速度矢量几乎为零,意味着最中间的流体应处于静止或极低流速状态,这种流态将促使小球表面产生高温热点。

|
图 4 两种排布方式的横截面速度矢量分布图(a) FCC排布,(b) BCC排布 Figure 4 Velocity vector distributions in the cross section of the two arrangement modes. (a) FCC arrangement mode, (b) BCC arrangement mode |
图 5给出了FCC排布下,不同竖直剖面上的温度、压力和速度分布云图。小球中心最高温度为1153 K,流体从进口到出口的总压降为1323 Pa,平均流经每层小球的压降约为265 Pa。FCC排布结构下的每个孔隙是由6个相切小球围成的,且每个孔隙的形状一致,对比45°和90°方向的压力和速度分布可以看出,45°方向的速度和压力梯度明显高于90°方向,这会导致孔隙里的漩涡出现各向异性的特征,影响熔盐与流体的换热特性,显然45°方向的流体与小球的换热效果更佳,小球表面温度更低。

|
图 5 FCC排布的温度、压力、速度分布(a) 45°视图,(b) 90°视图 Figure 5 Temperature, velocity and pressure distributions of the FCC arrangement mode. (a) View of the 45°, (b) View of the 90° |
图 6给出了BCC排布下,不同竖直剖面上的温度、压力和速度分布云图。小球中心最高温度为1155 K,流体从进口到出口的总压降为574 Pa,平均流经每层小球的压降约为82 Pa。BCC排布结构的各个孔隙形状也一致,对比45°和90°方向的压力和速度分布可以发现孔隙里的漩涡同样也存在各向异性的特征。流体在90°方向的速度分布出现极强的各向异性,竖直方向速度较大,容易造成流动分离,从而在下游产生较强的漩涡,使该处的流体与小球换热效果更佳,小球表面温度更低,而在45°方向上流体速度普遍较小,小球表面温度更高。

|
图 6 BCC排布的温度、压力、速度分布(a) 45°视图,(b) 90°视图 Figure 6 Temperature, velocity and pressure distributions of the BCC arrangement mode. (a) View of the 45°, (b) View of the 90° |
为了更好地了解燃料球表面及周围的流场分布,本文选择了两种结构下的中间小球进行对比分析。图 7为FCC和BCC排布下中间小球的局部流线图。由图 7可以看出,这两种排列方式下流型之间的差异。由于BCC排列方式可以形成无阻碍的流通通道,因此流线较为平直;而FCC排列中,燃料球会出现在流道中间,阻碍冷却剂流动,因此流线较为曲折。这种差异会影响熔盐流过球床时的流动压降以及熔盐与球面的换热效果。

|
图 7 FCC (a)和BCC (b)的局部流线图 Figure 7 Streamline distributions of the local flow for the FCC (a) and BCC (b). |
图 8给出了FCC和BCC排布下中间小球的表面温度分布三维图。由图 8可知,两种排布结构的中间小球都出现了高温热点,并且都位于球间接触点偏下游位置处,并且下游的热点温度高于上游的热点温度。对比图 8(a)、(b)可以看出,FCC排布的小球表面温度分布更为均匀,且热点温度远小于BCC排布。这主要是由于FCC排布结构对流体的搅混效果更明显,而BCC排布由于孔隙尺度存在强烈的各向异性,在热点位置处的流体速度极小,从而造成该区域传热恶化。另外,对比两个表面温度分布俯视图可以发现,BCC排布的中间小球底部温度分布不均匀,在最低位置处也出现了热点。

|
图 8 中间小球表面温度分布 (a) FCC排布(依次为俯视图、侧视图、仰视图),(b) BCC排布(依次为俯视图、侧视图、仰视图) Figure 8 Surface temperature distributions of intermediate ball. (a) FCC arrangement mode (top view, side view, upward view), (b) BCC arrangement mode (top view, side view, upward view) |
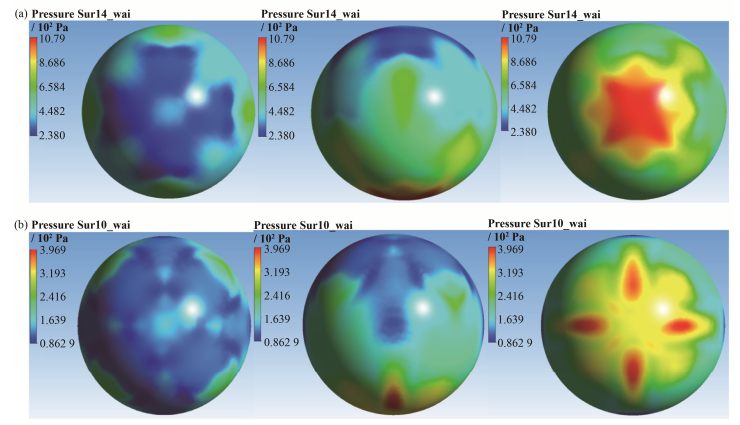
图 9给出了中间小球的表面压力分布。对于FCC排布,表面压力从底部到顶部的压降约为700Pa,且最高压力出现在小球最低位置,因为该处的流体几乎竖直冲击小球底部,该压力相当于流体流动的滞止压力。而对于BCC排布,沿球面的压降约为140 Pa,远小于FCC排布,且最高压力并非在小球的最底部。
|
图 9 中间小球表面压力分布 (a) FCC排布(依次为俯视图、侧视图、仰视图),(b) BCC排布(依次为俯视图、侧视图、仰视图) Figure 9 Surface pressure distributions of intermediate ball. (a) FCC arrangement mode (top view, side view, upward view), (b) BCC arrangement mode (top view, side view, upward view) |
针对TMSR-SF系统,利用计算流体力学分析程序,选取FCC和BCC两种规则的小球排布方式进行建模,分析了不同排布方式下堆芯的流动与换热特性,结果表明:
1) FCC排布下的流线呈现出周期性弯曲,BCC排布下的流线大体呈直线。FCC排布形成的间隙内速度矢量分布较为均匀,有利于排出周围小球的热量,BCC排布下间隙最中间区域的速度矢量几乎为零,使得小球表面产生高温热点。
2) FCC排布下,小球中心最高温度为1153 K,流体从进口到出口的总压降为1323 Pa,流体在45°方向的速度和压力梯度明显高于90°方向。BCC排布下,小球中心最高温度为1155 K,流体从进口到出口的总压降为574 Pa,流体在90°方向的速度和压力梯度明显高于在45°方向。FCC排布的流动压降明显大于BCC排布。
3) 对于单个中间小球,FCC排布的小球表面温度分布更为均匀,且热点温度远小于BCC排布。FCC排布下,表面压力从底部到顶部的压降约为700 Pa,最高压力出现在小球最低位置,BCC排布下,沿球面的压降约为140 Pa,远小于FCC排布,且最高压力并非在小球的最底部。
| [1] |
李华, 秋穗正, 苏光辉, 等. 球床堆内冷却剂流动与传热特性的CFD研究[J].
核动力工程, 2009, 30(S1): 39–43.
LI Hua, QIU Suizheng, SU Guanghui, et al. CFD research on flow and heat transfer characteristics of coolant in pebble bed reactor core[J]. Nuclear Power Engineering, 2009, 30(S1): 39–43. DOI: 10.7538/yzk.2009.39.5S1.0039 |
| [2] |
李健, 宋小明, 鲁剑超, 等. 基于有序堆积球床的单相阻力特性实验研究与数值模拟[J].
原子能科学与技术, 2012, 46(S1): 807–810.
LI Jian, SONG Xiaoming, LU Jianchao, et al. Experimental research and numerical simulation on single phase flow resistance characteristics of orderly packed bed[J]. Atomic Energy Science and Technology, 2012, 46(S1): 807–810. DOI: 10.13832/j.jnpe.2012.S1.0807 |
| [3] |
潘登, 余笑寒, 邹杨, 等. 规则球床堆熔盐流动压降与对流换热CFD模拟[J].
核技术, 2016, 39(8): 080604.
PAN Deng, YU Xiaohan, ZOU Yang, et al. CFD-simulation of structured packed beds molten salt reactors on pressure drop and heat transfer[J]. Nuclear Techniques, 2016, 39(8): 080604. DOI: 10.11889/j.0253-3219.2016.hjs.39.080604 |
| [4] | Song S X, Cai X Z, Liu Y F, et al. Pore scale thermal hydraulics investigations of molten salt cooled pebble bed high temperature reactor with BCC and FCC configurations[J]. Science and Technology of Nuclear Installations, 2014(3): 1–16. DOI: 10.1155/2014/589895 |
| [5] |
焦小伟, 王凯, 何兆忠, 等. 固态熔盐堆全厂断电ATWS事故工况下的堆芯安全探讨[J].
核技术, 2015, 38(2): 020604.
JIAO Xiaowei, WANG Kai, HE Zhaozhong, et al. Core safety discussion under station blackout ATWS accident of solid fuel molten salt reactor[J]. Nuclear Techniques, 2015, 38(2): 020604. DOI: 10.11889/j.0253-3219.2015.hjs.38.020604 |
| [6] |
TMSR-SFl堆物理分总体. 10 MWt TMSR-SFl总体物理方案和参数[R].上海:中国科学院上海应用物理研究所, 2013.
Reactor Physics Department of TMSR-SF1.Physics programs and parameters for 10-MWt TMSR-SF1[R]. Shanghai: Shanghai Institute of Applied Physics, Chinese Academy of Sciences, 2013. |
| [7] |
梅牡丹, 邵世威, 何兆忠, 等. 固态钍基熔盐堆概率安全评价始发事件分析研究[J].
核技术, 2014, 37(9): 090601.
MEI Mudan, SHAO Shiwei, HE Zhaozhong, et al. Research on initial event analysis for solid thorium molten salt reactor probabilistic safety assessment[J]. Nuclear Techniques, 2014, 37(9): 090601. DOI: 10.11889/j.0253-3219.2014.hjs.37.090601 |
| [8] |
靖剑平, 刘雅宁, 贾斌, 等. 10 MWt固态燃料熔盐堆控制棒失控抽出事故分析[J].
核技术, 2016, 39(10): 100604.
JING Jianping, LIU Yaning, JIA Bin, et al. Accident analyses of uncontrolled rod cluster control assembly bank withdrawal for 10-MWt thorium-based molten salt reactor-solid fuel[J]. Nuclear Techniques, 2016, 39(10): 100604. DOI: 10.11889/j.0253-3219.2016.hjs.39.100604 |
| [9] | Liu L M, Zhang D L, Lu Q, et al. Preliminary neutronic and thermal-hydraulic analysis of a 2-MW thorium-based molten salt reactor with solid fuel[J]. Progress in Nuclear Energy, 2016, 86: 1–10. DOI: 10.1016/j.pnucene.2015.09.011 |
| [10] |
牛强, 宋士雄, 魏泉, 等. 熔盐冷却球床堆热通道热工水力特性数值分析[J].
核技术, 2014, 37(7): 070602.
NIU Qiang, SONG Shixiong, WEI Quan, et al. Thermal-hydraulics numerical analyses of pebble bed advanced high temperature reactor hot channel[J]. Nuclear Techniques, 2014, 37(7): 070602. DOI: 10.11889/j.0253-3219.2014.hjs.37.070602 |


