2. 中国科学院大学 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
圆柱形容器内单一粒径颗粒堆积的问题在工业中应用广泛,熔盐冷却球床堆[1]燃料球的装料问题就是代表性的应用之一。颗粒的堆积形态直接决定着燃料-冷却剂的反应特性及传热效率。在某些工况下颗粒孔隙率的变化也是反应堆安全所关心的问题之一,比如地震引发的改变燃料球的松散度甚至包络面,而燃料球的堆积密度的变化会影响堆芯临界以及安全余量[2];不同的初始燃料球堆积对在线换料过程的影响,包括循环达到稳定所需的时间和稳定后的孔隙率分布等。如何高效地生成不同孔隙率分布的颗粒堆积也就有着现实的意义。
颗粒堆积的方法按照是否考虑颗粒间的真实受力而分为两类:
第一类是基于几何的方法来构造颗粒堆积,这类方法不考虑颗粒之间的受力,而是依据某些几何限制来移动颗粒从而构造出堆积结构。
Mueller[3]采用顺序放置颗粒位置的方式构造圆柱容器内的颗粒堆积。首先放置容器最底层的颗粒,底层之上的颗粒依据其是否紧贴容器壁而分为两类,且按照在竖直方向上颗粒可以保持稳定的原则来依次插入新颗粒。整个算法是确定性的,对于小床径比的堆积比较准确,然而对于大床径比的堆积就有一定偏差。
区域分解也是构造堆积的几何方法之一,不同的分解方式依赖于各自分解区域的策略。Luchnikov[4]利用维诺网格将容器离散成一个个元胞,然后在元胞中放置颗粒。Jerier[5]则是将堆积区域用四面体网格分解开,先在生成的四面体网格内放置与其内切的颗粒,然后检测初始堆积的空洞部分并填充入新的颗粒,由此生成有一定粒径宽度的密实堆积,算法也适用于复杂几何容器。
此外,蒙特卡罗方法也是构造堆积常用的方法之一,首先随机生成一系列颗粒位置,然后在此基础上,依据一定的概率去不断修正重叠颗粒的位置从而达到稳定。Soontrapa[6]用改进的蒙特卡罗方法研究了燃料电池中催化剂颗粒的堆积问题。对于初始随机生成的颗粒,让其在随机的方向上运动,运动的步长由算法中定义的势函数所确定。该算法其实是几何堆积方法和动力学方法的结合,因为其势函数本质上考虑了实际颗粒在接触过程中的受力情况。改进的蒙特卡罗方法可以在保持堆积密度偏差不大的情况下明显减小堆积模拟的计算时间,要比单纯的随机方向的运动搜索更加有效。
第二类是基于动力学的方法来构造颗粒堆积。基于几何的堆积构造方法由于不考虑颗粒间具体的弹性作用力,从而有较高的计算效率,但同时也意味着丢失了颗粒间的动力学信息。为了更精确地模拟实际堆积,颗粒之间的真实碰撞过程必须予以考虑。离散元法[7]作为计算颗粒运动的动力学方法,被广泛地运用到模拟颗粒运动过程[8]和颗粒堆积的构造过程中。
Li等[9]针对离散元法模拟高温球床型反应堆初始装料效率低的问题,首先随机生成允许颗粒重叠的初始分布,然后用简化的离散元受力模型去消除颗粒间的重合来达到稳态。颗粒间的法向接触力与重合量程简单的线性关系,由此提高计算速度。
Ougouag等[10]针对球床反应堆在地震等事故工况下燃料球堆积的密实化,用离散元方法去模拟振动密实的过程。An等[11-12]的离散元模拟和振动实验也说明了振动可以显著提高体系的密实度,对于特定的颗粒系统,存在最优的振动频率和振幅对应达到最密实堆积,太大和太小都不利于密实程度的增加。
实际情况中堆积的形成往往是让颗粒群基于重力不断落入容器中直至达到指定数目的颗粒。这种基于重力落球的堆积方法可以用离散元法从流程上去严格模拟。虽然离散元法模拟颗粒堆积的过程更加贴近于实际堆积组态,但其很小的时间步长导致了很大的运算量。一些学者在运用离散元法的过程中常常使用比实际颗粒小的刚度系数来增大时间步长,尤其是在颗粒和流体的耦合计算中[13]。但对于堆积问题,最终孔隙率的值直接取决于颗粒的硬度,太大的颗粒重合量将导致严重失真,这就意味着颗粒刚度系数并不能比实际值小太多。
为了综合离散元法去贴近于实际物理过程和采用很低的刚度系数去提高计算效率两方面的优势,本文提出了基于两个阶段的重力落球堆积算法,算法分为软球自由下落和硬球缓慢膨胀两个阶段,两阶段中引入不同的杨氏模量和能量耗散机制。通过调节下落过程的摩擦系数和杨氏模量、膨胀过程中的摩擦系数这三个参数来调节最终的孔隙率和计算效率。
1 数学模型离散元法是计算散体力学行为的数值方法,Cundall等[7]最早提出并发展了相应的计算程序。离散元法的核心是牛顿定律,半径分别为Ri和Rj,位于ri和rj的相邻的两个颗粒i和j,颗粒i的运动方程为:
| ${m_i}\frac{{{\text{d}}{{\overrightarrow V }_i}}}{{{\text{d}}t}} = {m_i}\overrightarrow g + \sum\limits_{j = 1}^{{N_c}} {\left( {{{\overrightarrow f }_{n, ij}} + {{\overrightarrow f }_{t, ij}}} \right)} $ | (1) |
| ${I_i}\frac{{{\text{d}}{{\overrightarrow w }_i}}}{{{\text{d}}t}} = \sum\limits_{j = 1}^{{N_c}} {\left( {{{\overrightarrow r }_i} \times {{\overrightarrow f }_{t, ij}}} \right)} $ | (2) |
式中:下标n和t分别代表切向和法向分量;
颗粒之间的法向接触力和切向接触力依据简化的Hertz-Mindlin-Deresiewicz接触模型计算:
| ${\overrightarrow f _{n, ij}} = \left( {-{k_n}\delta _{n, ij}^{3/2}-{\gamma _n}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V} }_{n, ij}} \cdot {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {n} }_{ij}}} \right){\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {n} _{ij}}$ | (3) |
| ${\overrightarrow f _{t, ij}} =-\min \left( {{k_t}{\delta _{t, ij}} + {\gamma _t}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V} }_{t, ij}} \cdot {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {t} }_{ij}}, \mu \left| {{{\overrightarrow F }_{n, ij}}} \right|} \right) \cdot {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {t} _{ij}}$ | (4) |
式中:k和γ代表硬度和阻尼系数;
| ${\delta _t} = \int\limits_{{t_0}}^t {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V} }_{t, ij}} \cdot {\text{d}}t} $ | (5) |
| ${\delta _n} = {R_i} + {R_j}-\left| {{{\overrightarrow r }_i}-{{\overrightarrow r }_j}} \right|$ | (6) |
对三角形墙壁单元j有:
| ${\delta _n} = {R_i}-L$ | (7) |
式中:L为颗粒i在三角形j法向上的投影。
刚度系数k和阻尼系数γ为:
| ${k_n} = \frac{4}{3}{E^*}\sqrt {{R^*}} $ | (8) |
| ${k_t} = \frac{{1-2v}}{{2(1-v)}}{k_n}$ | (9) |
| ${\gamma _n} =-2\sqrt {\frac{5}{6}} \frac{{\ln \varepsilon }}{{\sqrt {{{\ln }^2}\varepsilon + {{\pi }^2}} }}\sqrt {\frac{3}{2}{k_n}{m^*}} $ | (10) |
| ${\gamma _n} = {\gamma _t}$ | (11) |
其中:R、m、E分别为:
| $\frac{1}{{{R^*}}} = \frac{1}{{{R_i}}} + \frac{1}{{{R_j}}}$ | (12) |
| $\frac{1}{{{m^*}}} = \frac{1}{{{m_i}}} + \frac{1}{{{m_j}}}$ | (13) |
| $\frac{1}{{{E^*}}} = \frac{1}{{{E_i}}} + \frac{1}{{{E_j}}}$ | (14) |
式中:Ei和Ej分别是颗粒i和颗粒j的杨氏模量;ν为泊松比;ε是恢复系数。
最大的时间步长由瑞利时间步长决定:
| ${T_{\text{R}}} = \frac{{\pi R\sqrt {{\rho _p}/G} }}{{(0.163\;1v + 0.876\;6)}}$ | (15) |
其中:剪切模量为:
| $G = \frac{E}{{2(1 + v)}}$ | (16) |
为了避免数值震荡,取瑞利时间步长的30%作为模拟所使用的步长[14]。不失一般性,颗粒-墙壁和颗粒-颗粒之间的物性参数选取相同。
2 两阶段堆积算法 2.1 自由下落阶段初始堆积的生成采用类似EDEM软件中颗粒工厂的方式[14]。首先在容器上方的某一个圆柱体空间内定义为颗粒工厂,与堆积容器的z轴重合,半径相等,并且距离设置为几个颗粒直径的高度,随后在工厂内随机产生颗粒,如果与已有颗粒重叠则舍弃该颗粒,重复随机过程直至产生指定数目的颗粒。通过控制工厂内颗粒的初始速度来调节下落颗粒的密度。不失一般性,本文取颗粒的初始下落速度为0。从刚开始生成工厂颗粒到最终稳定初始堆积过程见图 1。

|
图 1 堆积过程(a)在工厂中随机生成颗粒,(b)颗粒下降过程,(c)堆积稳定 Figure 1 Packing process. (a) Particles are generated randomly in factory, (b) The falling process of particles, (c) Stable state of packing |
在自由下落这一阶段,给颗粒设置不同的杨氏模量和摩擦系数来生成含有不同程度颗粒间重合量的初始堆积,膨胀阶段再耗散掉体系的弹性势能来更新颗粒位置直至达到指定的颗粒间重合量。
离散元计算过程中时间步长反比于法向刚度系数(Δt∝kn-1/2),所以许多文献中采用小于实际杨氏模量的值来提高自由下落阶段的离散元计算效率[15]。另一方面,太小的刚度系数会导致过度失真的重合[13],即重叠量大于单个球的半径,所以杨氏模量的取值有下限。本文分别以8种杨氏模量和5种摩擦系数来生成不同组合的初始堆积。
为了避免小的床径比带来的壁面效应同时减少计算量,本文选取床径比为20的圆柱容器作为模拟对象。下落过程中离散元模拟参数见表 1。
| 表 1 自由下落阶段颗粒物性 Table 1 Particle parameters in falling process. |
工业中很多情况下材料杨氏模量很大,以至于颗粒重叠量非常小。对于球床型氟盐冷却高温堆(Pebble-bed Fluoride-salt-cooled High-temperature Reactor, PB-FHR)堆芯,石墨颗粒漂浮在液体冷却剂中,燃料和冷却剂密度相差很小,净重力加速度约为大气环境中的1/10,所以此时颗粒重叠量更小。考虑到计算量的问题,本文在自由膨胀阶段取颗粒的杨氏模量为1×1011 Pa。
初始堆积含有较大的重叠量,本阶段中引入实际的杨氏模量导致系统有极大的弹性势能,可是堆积稳定后系统的弹性势能和动能可以认为是0。阻尼可以耗散一部分能量,但是弹性能主要转化为颗粒的机械能,阻尼耗散所占的比重很小,且缓慢膨胀要求颗粒速度很小,所以需要人为引入新的耗散机制,让初始堆积在缓慢膨胀的过程中将弹性能耗散掉,最终得到稳定的颗粒堆积。其与硬球下落得到堆积的相似性通过整体孔隙率和径向孔隙率分布两个量来衡量。
与传统的重力落球方法相比,膨胀阶段颗粒的位移很小,一般只有几个球直径的量级,所以膨胀阶段占用的计算量与传统方法相比可以忽略不计,但与采用低杨氏模量的自由下落阶段相比其计算负荷并不一定很小。随着膨胀的继续,颗粒间平均重叠量减小,体系的弹性能减小,一定的时间间隔内颗粒运动的平均位移减少,体现在宏观上是堆积演化变缓慢,此时就可以适当增大冻结周期内的时间步长来提高计算效率。
耗散机制如下:追踪颗粒群的最大位移一旦超过颗粒半径的1/N,就将所有颗粒的速度全部重置为0,并依据最大重叠量重新计算下一个阶段内的时间步长。
膨胀太快会使得初始堆积在快速散开的过程中形成颗粒间大的不稳定的空洞,在重力作用下坍塌,而太慢又会增加不必要的计算负荷。本文取触发冻结的最大颗粒位移为颗粒半径的1/5。
膨胀过程一直持续到最大重叠量逐渐减小并趋于恒定值。由于阻尼导致的耗散远小于冻结导致的能量损失,所以在膨胀阶段不考虑粘性阻尼和非粘性阻尼的影响,仅考虑摩擦系数对堆积演化的影响。实际过程中的颗粒间摩擦系数通常小于0.5,所以本文取5种不同的摩擦系数作为研究变量。
3 孔隙率计算圆柱形容器内径向孔隙率分布的计算,本文采用Mueller[16]提出的计算方式,用一系列等间距的环形截面去切割容器,每个截面上孔隙率等于未被球占据的面积和截面面积之比。通过用等间距的平面去切割容器,轴向孔隙率分布的计算方式与径向孔隙率分布的计算类似。靠近堆积顶部和底部的两层颗粒由于壁面效应的影响不能反映整个堆积的平均孔隙率,由于模拟的体系大小有限,所以平均孔隙率的计算中舍弃分别位于堆积顶部和底部的两层颗粒。整个堆积的平均孔隙率可以通过对轴向孔隙率分布做积分来得到:
| $\varepsilon = \int_{{H_{{\text{bottom}}}} + 2d}^{{H_{{\text{top}}}}-2d} {\varepsilon (z)} /({H_{{\text{top}}}}-{H_{{\text{bottom}}}}-4d)dz$ | (17) |
式中:Htop和Hbottom分别代表堆积最上端和最下端的轴向坐标。Zou等[17]给出了不同床径比条件下密实堆积和松散堆积平均孔隙率的计算公式。对于本文床径比为20的容器,松散堆积的孔隙率为0.407,密实堆积的孔隙率为0.374。
4 结果和讨论 4.1 下落杨氏模量对膨胀摩擦系数的弱化作用膨胀过程以自由下落阶段得到的堆积为初始状态,通过一系列冻结操作逐渐演化,最终得到稳定的堆积结构。在此过程中,通过控制下落阶段中的杨氏模量(Yi)和摩擦系数(ffall)、膨胀阶段的摩擦系数(fexpand)这三个参数来调控最终堆积的孔隙率。Yi、ffall和fexpand的取值见表 1,共有200种不同的系数组合来研究不同参数组合对堆积的影响。
图 2(a-h)显示了在8种下落杨氏模量的情况下不同膨胀摩擦系数和不同下落摩擦系数对应的孔隙率值。图 2中横坐标表示5种不同的fexpand,纵坐标表示堆积的孔隙率,f0到f4指5种不同的ffall。可见本文的算法生成堆积的孔隙率范围基本可以覆盖文献[17]给出的松散到密实堆积。
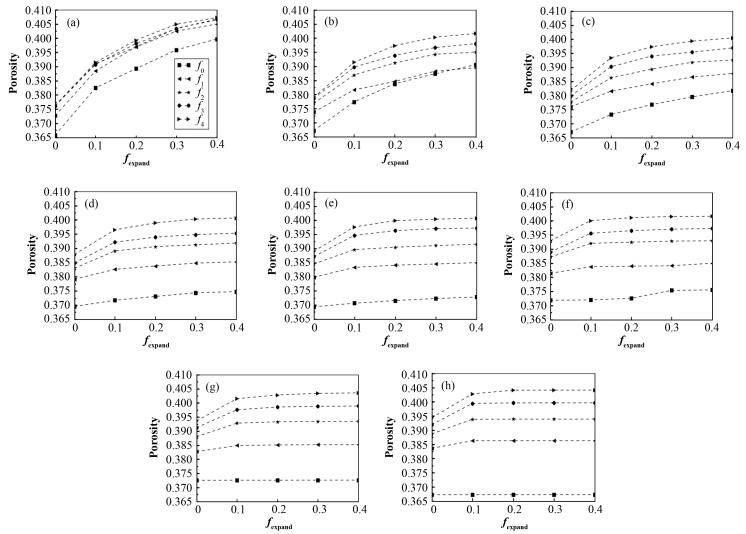
|
图 2 不同Yi下的摩擦系数-孔隙率关系 (a) Yi=1×106,(b) Yi=5×106,(c) Yi=1×107,(d) Yi=5×107,(e) Yi=1×108,(f) Yi=1×109,(g) Yi=1×1010,(h) Yi=1×1011 Figure 2 Relationship between friction coefficient and porosity with different Yi. (a) Yi=1×106, (b) Yi=5×106, (c) Yi=1×107, (d) Yi=5×107, (e) Yi=1×108, (f) Yi=1×109, (g) Yi=1×1010, (h) Yi=1×1011 |
图 2(g)和(h)所对应的孔隙率几乎一致,说明在一定颗粒物性的条件下,杨氏模量可以取值略小于真实值来加速计算,但超过一定限值就会由于堆积柔性的偏大导致计算失真。
由图 2可见,对于固定的Yi而言,曲线的斜率均非负,说明了fexpand对堆积孔隙率的正向作用。不同曲线的高度说明了ffall对堆积孔隙率的正向作用。这与实际堆积过程中的经验是一致的,即大的摩擦系数有助于颗粒间形成稳定的结构,从而降低体系的密实度。摩擦系数的减少使得颗粒稳定时的受力更多地依赖于相邻颗粒间的法向接触力,所以颗粒间的接触相对而言更加紧凑,密实度更高。
随着Yi的增大,曲线的平均斜率逐渐减小,说明大的Yi生成的初始堆积会削弱fexpand对堆积孔隙率的正向作用,因为大的杨氏模量对应的初始堆积具有小的颗粒间重合量,自由膨胀阶段每个颗粒改变自身的位置的空间就越小,所以fexpand对堆积孔隙率的正向作用也会相应减弱。
4.2 膨胀和硬球直接下落构成的堆积的相似性当下落阶段杨氏模量取值和膨胀阶段的杨氏模量一致且二者的摩擦系数也相等时,自由下落得到的堆积就是最终的稳定堆积,膨胀过程不再起作用。此时本文的堆积算法就退化为传统的硬球下落堆积算法。图 3(a)和(b)就可以代表硬球下落的松散和密实堆积。图 3(a-f)是三组下落杨氏模量所对应的最密实和最松散堆积的径向孔隙率分布。图 3的横坐标代表颗粒球心到容器壁的距离(以颗粒直径为单位长度)。可以发现不同的下落杨氏模量所构建出的堆积(Yi=1×106,Yi=1×108)和硬球下落生成的堆积(Yi=1×1011)具有基本一致的整体孔隙率和径向孔隙率分布。
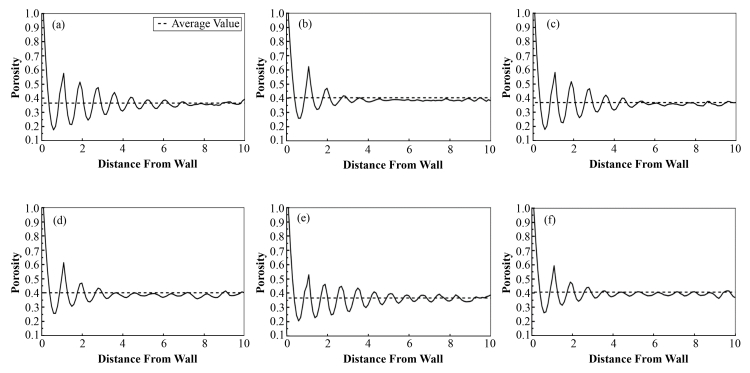
|
图 3 不同参数下的径向孔隙率分布 (a) 1×1011、0.0、0.0,(b) 1×1011、0.4、0.4,(c) 1×108、0.0、0.0,(d) 1×108、0.4、0.4,(e) 1×106、0.0、0.0,(f) 1×106、0.4、0.4 Figure 3 Radial porosity distribution with different Yi, fexpand and ffall (a) 1×1011, 0.0, 0.0, (b) 1×1011, 0.4, 0.4, (c) 1×108, 0.0, 0.0, (d) 1×108, 0.4, 0.4, (e) 1×106, 0.0, 0.0, (f) 1×106, 0.4, 0.4 |
传统的离散元法通过颗粒自由下落达到稳定来模拟堆积过程时,也可以取略小的杨氏模量Yc来模拟。为了估计两阶段算法在计算效率上的优势,考虑自由下落阶段取远小于Yc的模量而膨胀阶段为Yc的两阶段过程。考虑到膨胀过程中颗粒的平均位移在几个颗粒直径量级,远小于真实情况下自由下落所经历的位移,所以略去其计算时间。这时本文算法中小的Yi所获得的计算效率的提升就可以认为是整个算法效率的提升。作为特例,当Yi取Yc时,膨胀过程缩短为0,fexpand的效果不复存在,本文的算法就退化成传统的重力落球算法。图 4在对数坐标轴上显示了不同的Yi按式(15)所采用的计算时间步长。当Yi取接近真实值的1×1011时,其对应的时间步长为5×10-6s,而在不出现虚假接触的限定下取1×106时,时间步长约为2×10-4s,时间步长两个量级提升,而对应的计算量减少两个量级。
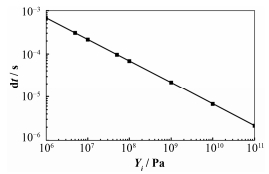
|
图 4 下落阶段杨氏模量和时间步长的关系 Figure 4 Relationship between Yi and time step in falling process. |
本文提出的颗粒堆积算法针对圆柱形容器中单粒径颗粒的堆积问题,可以生成从松散到密实范围内的颗粒堆积,为PB-FHR堆芯提供不同孔隙率的燃料球分布。大的fexpand和ffall导致大的孔隙率,反之亦然。Yi愈大,离散元方法的计算时间步长愈小,相应的计算负荷愈重,同时也会削弱fexpand对堆积孔隙率的正向作用。
对于指定孔隙率的堆积,通过下落过程中的摩擦系数和杨氏模量、膨胀过程中的摩擦系数这三个参量来控制密实度。其中摩擦系数对孔隙率的影响很大。在fexpand和ffall相等的情况下,不同的Yi对应着基本一致的整体孔隙率和径向孔隙率分布。建议首先选择合适的Yi确定大致可接受的计算量,然后调节两个阶段的摩擦系数去控制最终堆积的密实度。
| [1] | Forsberg C W, Peterson P F, Pickard P S. Molten-salt-cooled advanced high-temperature react or for production of hydrogen and electricity[J]. Nuclear Technology, 2003, 144(3): 289–302. DOI: 10.13182/nt03-1 |
| [2] |
彭超, 朱兴望, 张国庆, 等. 采用SCALE计算氟盐冷却高温堆产氚量的一些问题[J].
核技术, 2015, 38(8): 080601.
PENG Chao, ZHU Xingwang, ZHANG Guoqing, et al. Issues in the calculation of the tritium production of the fluoride-salt-cooled high-temperature reactors using SCALE[J]. Nuclear Techniques, 2015, 38(8): 080601. DOI: 10.11889/j.0253-3219.2015.hjs.38.080601 |
| [3] | Mueller G E. Numerical simulation of packed beds with monosized spheres in cylindrical containers[J]. Powder Technology, 1997, 92(2): 179–183. DOI: 10.1016/S0032-5910(97)03207-5 |
| [4] | Luchnikov V, Gavrilova M L, Medvedev N N, et al. The voronoi-delaunay approach for the free volume analysis of a packing of balls in a cylindrical container[J]. Future Generation Computer Systems, 2002, 18(5): 673–679. DOI: 10.1016/S0167-739X(02)00032-8 |
| [5] | Jerier J F, Imbault D, Donze F V, et al. A geometric algorithm based on tetrahedral meshes to generate a dense polydisperse sphere packing[J]. Granular Matter, 2009, 11(1): 43–52. DOI: 10.1007/s10035-008-0116-0 |
| [6] | Soontrapa K, Chen Y. Mono-sized sphere packing algorithm development using optimized Monte Carlo technique[J]. Advanced Powder Technology, 2013, 24(6): 955–961. DOI: 10.1016/j.apt.2013.01.007 |
| [7] | Cundall P A, Strack O D. A discrete numerical model for granular assemblies[J]. Geotechnique, 1979, 29(1): 47–65. DOI: 10.1680/geot.1979.29.1.47 |
| [8] |
杨星团, 刘志勇, 胡文平, 等. HTR-10堆芯球流运动的唯象学DEM模拟[J].
原子能科学技术, 2013, 47(12): 2231–2237.
YANG Xingtuan, LIU Zhiyong, HU Wenping, et al. DEM simulation of pebble flow in HTR-10 core by phenomenological method[J]. Atomic Energy Science and Technology, 2013, 47(12): 2231–2237. DOI: 10.7538/yzk.2013.47.12.2231 |
| [9] | Li Y, Ji W. A collective dynamics-based method for initial pebble packing in pebble flow simulations[J]. Nuclear Engineering and Design, 2012, 250: 229–236. DOI: 10.1016/j.nucengdes.2012.05.020 |
| [10] | Ougouag A M, Cogliati J J. Earthquakes and pebble bed reactors: time-dependent densification[J]. Mathematics & Computation and Supercomputing in Nuclear Applications Monterey, 2007. DOI: 10.1.1.204.9984. |
| [11] | An X Z, Yang R Y, Zou R P, et al. Effect of vibration condition and inter-particle frictions on the packing of uniform spheres[J]. Powder Technology, 2008, 188(2): 102–109. DOI: 10.1016/j.powtec.2008.04.001 |
| [12] | An X Z, Li C X. Experiments on densifying packing of equal spheres by two-dimensional vibration[J]. Particuology, 2013, 11(6): 689–694. DOI: 10.1016/j.partic.2012.06.019 |
| [13] | Alobaid F, Baraki N, Epple B. Investigation into improving the efficiency and accuracy of CFD/DEM simulations[J]. Particuology, 2014, 16: 41–53. DOI: 10.1016/j.partic.2013.11.004 |
| [14] | Solutions D. EDEM v2.3 user guide[Z]. Edinburgh, UK: DEM Solutions Ltd, 2010. |
| [15] | Toit C G D. Radial variation in porosity in annular packed beds[J]. Nuclear Engineering and Design, 2008, 238(11): 3073–3079. DOI: 10.1016/j.nucengdes.2007.12.018 |
| [16] | Mueller G E. Radial porosity in packed beds of spheres[J]. Powder Technology, 2010, 203(3): 626–633. DOI: 10.1016/j.powtec.2010.07.007 |
| [17] | Zou R, Yu A. The packing of spheres in a cylindrical container: the thickness effect[J]. Chemical Engineering Science, 1995, 50(9): 1504–1507. DOI: 10.1016/j.nucengdes.2012.05.020 |


