在γ射线编码板成像系统中，重建算法的好坏直接影响重建图像的质量。对于修正均匀冗余阵列(Modified Uniformly Redundant Arrays, MURA)编码模式下的编码板成像系统，研究人员对一些重建算法进行过对比研究^[1]，而最大似然期望最大化(Maximum Likelihood Expectation Maximization, MLEM)算法由于能对噪声进行很好的抑制，且在投影数据不完全时可以对图像进行很好的重建而成为主流算法。MLEM算法的缺点是：在编码板投影图像所含噪声较大时，随着迭代次数的增加，噪声对重建图像的影响会相应放大。目前对于MLEM算法的改进主要集中在核医学领域，如有序子集期望最大化(Ordered Subset Expectation Maximization, OSEM)算法、子集序列期望最大化(Subset Sequence Expectation Maximization, SSEM)算法以及计算调控有序子集期望最大化(Count Regulated Ordered Subset Expectation Maximization, CROSEM)算法等^[2-3]。由于编码板成像与医学成像在数据采集方式上的不同，医学成像中的相关算法不能直接应用于编码板成像。在编码板成像中，有关MLEM算法改进的论述较少。

对于编码板成像系统，噪声大小直接影响其图像质量。为了抑制噪声对重建图像的影响，通过理论证明^[4]，可以用两个互补的编码孔经重建所得图像相减来减小噪声对重建图像的影响。本文基于该思想对编码板成像中的MLEM算法进行改进，提出MLEM互补算法。该算法在传统MLEM算法公式中加入编码板修正因子α，在迭代算法中进行互补编码板相减计算。MLEM互补算法中最佳修正因子α值的选取与编码板线性衰减系数与厚度的乘积有关。通过蒙特卡罗模拟给出算法最佳修正因子的α-μt拟合公式，并进行实验验证。实验结果证明，与传统MLEM算法相比，MLEM互补算法在成像时可以更有效地抑制噪声。采用模拟所得α-μt拟合公式，可以给出不同情况下MLEM互补算法最佳α值。

MLEM算法是基于泊松统计模型的最大贝叶斯后验概率的图像复原方法，该算法由Shepp等^[5]于1982年提出。MLEM算法主要分为两步：1) 计算完全投影数据的似然函数在测定数据及当前参数估计值下的期望；2) 求出使期望最大化的参数估计值。

在γ辐射编码成像中MLEM算法^[6-8]表示为：

式中：${f^k}(x, y)$为第k次图像估计值；$p(x, y)$为实测投影值；$h(x, y)$为编码函数；*表示卷积运算；$\otimes $代表相关运算。从式(1)中可知，MLEM迭代算法包含了“投影”和“反投影”两个过程。p′(x, y)=f^k(x, y)*h(x, y)是根据第k次放射源强度分布的迭代估计值和编码函数所计算得出的投影估计值。式(2)是将理论投影值与实际测定值相比较，将其比值做相关运算，并反投影到第k次放射源强度分布图像，对之前的估计值做出修正，使其逐渐逼近目标图像。

基于互补编码板相减去除噪声的思想，在进行MLEM迭代时，对迭代公式(1)中的编码函数h(x, y)进行修正。令h(x, y)=h′(x, y)+αh″(x, y)，其中：h′(x, y)为正常编码函数；h″(x, y)为h′(x, y)逆时针旋转90°所得编码函数；α为算法修正因子，取值范围为(-0.8, 0)。将h(x, y)带入迭代公式，可得：

在计算第k次放射源强度分布的迭代估计值和编码函数所计算得出的投影估计值时使用互补编码板相减去噪的方式对噪声进行抑制。由式(2)可知，由于在计算时对$p'(x, y)$进行了噪声抑制，使得实际测定值$p(x, y)$与修正理论投影值$p'(x, y)$的比值对重建图像的修正效果更好。将该值与修正后的h(x, y)做相关运算，使得迭代算法再次对噪声进行抑制，进一步减少噪声对重建图像的影响。

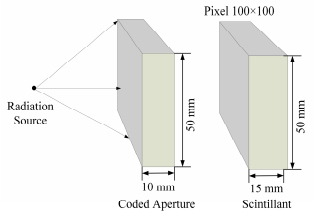
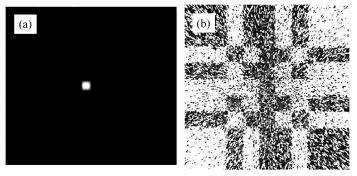
使用蒙特卡罗模拟软件MCNP5 (Monte Carlo N Particle Transport Code 5)对γ辐射编码板成像过程进行模拟，得到实验所需编码板投影数据。建立的γ辐射编码板成像模型示意图如图 1所示。编码板以11×11扩展模式的MURA编码板为基础，几何尺寸为50mm×50mm×10mm，采用方孔模式，孔径2mm，材料选用铅；点源位于视野中心轴线，距编码板500mm处，能量为662keV；探测器材料选用锗酸铋(Bi₂O₃-GeO₂, BGO)闪烁晶体，几何尺寸为50mm×50mm×15mm，距编码板20mm，计数时，将BGO晶体模型按100×100×1进行网格划分，并采用*F8计数卡对每个网格内沉积能量进行记录。通过蒙特卡罗模拟所得理想点源图像及其投影图像如图 2所示。

图 1

图 1 编码板模型示意图 Figure 1 Diagram of coded aperture model.

图 2

图 2 理想点源(a)和点源投影(b)图像 Figure 2 Simulated point source (a) and projection image (b).

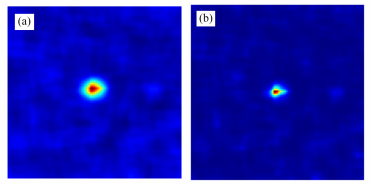
采用蒙特卡罗模拟所得编码板投影数据，分别通过MLEM算法和MLEM互补算法对图像进行重建。图 3为MLEM算法与MLEM互补算法(α=-0.6)在迭代次数n=5时的重建图像。由图 3可知，两种算法都可对模拟编码图像进行有效重建。采用MLEM互补算法对模拟图像进行重建，其对噪声的抑制效果更好，重建图像更接近模拟的点源图像。通过直接观察法可知，MLEM互补算法的成像效果要优于传统的MLEM算法。

图 3

图 3 MLEM算法(a)与MLEM互补算法(b)投影数据重建图像 Figure 3 Reconstructed image by MLEM iteration (a) and complementary MLEM iteration (b).

对重建图像进行评估时，主观评价往往很难判断算法的优劣。为进一步验证算法的有效性，在对重建图像的质量进行评价时，采用归一化均方误差E (Normalized Root Mean Square Error, NRMSE)以及相关系数r (Correlation Coefficient, CC)这两种定量方法对重建图像的质量进行评价。用归一化均方误差衡量算法的接近程度，相关系数衡量重建图像与原图像相似程度^[9]。NRMSE与CC评价标准的值E和r定义分别为：

式中：${x_{ij}}$和${\bar x_{ij}}$分别为真实图像灰度值和真实图像平均灰度值；${x'_{ij}}$和${\overline {x'} _{ij}}$分别为重建图像灰度值和重建图像平均灰度值。归一化均方误差的值表示图像与真实图像的接近程度，其值越小，图像重建效果越好；相关系数的值表示重建图像与真实图像的相似度，其值越大，重建图像与真实图像越接近。表 1为MLEM算法和MLEM互补算法迭代次数n=5时对模拟投影数据重建图像的NRMSE和CC值。由表 1可知，MLEM互补算法在两种评价下，皆优于MLEM算法，图像重建质量更好。

表 1

表 1 MLEM算法和MLEM互补算法NRMSE与CC值 Table 1 NRMSE and CC by MLEM and complementary MLEM algorithm. 算法Algorithm NRMSE CC MLEM 21.04 0.11 MLEM互补 Complementary MLEM 6.06 0.15

表 1 MLEM算法和MLEM互补算法NRMSE与CC值 Table 1 NRMSE and CC by MLEM and complementary MLEM algorithm.

为验证模拟结果的正确性，通过实验对算法的有效性进行验证。实验中编码板以11×11扩展的MURA编码模式为基础，编码板几何尺寸分别为50mm×50mm×10mm、50mm×50mm×20mm、50mm×50mm×30mm，孔型为方孔，孔径2mm，材料选用铅；探测器由50mm×50mm×10mm的BGO阵列晶体，耦合滨松H8500位置灵敏光电倍增管组成，探测器距编码板20mm。点源采用强度3.7×10⁴Bq的¹³⁷Cs源，位于视野中心轴线，距编码板500mm处。

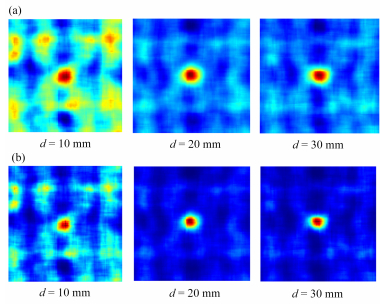
采用实验所得编码板投影数据，分别通过MLEM算法和MLEM互补算法对图像进行重建。图 4为MLEM算法和MLEM互补算法在迭代次数n=5时对三种厚度编码板实测投影重建图像。由图 4(a)可知，随着编码板厚度的增加，MLEM算法重建图像的背景噪声越来越小，图像质量逐步提高。由图 4(b)可知，采用MLEM互补算法进行图像重建时，在编码板厚度相同的情况下，MLEM互补算法的重建结果比MLEM算法的重建结果对噪声的抑制更明显。

图 4

图 4 MLEM算法(a)与MLEM互补算法(b)实验数据重建图像 Figure 4 Reconstructed images by MLEM (a) and complementary MLEM iteration algorithm (b).

表 2为MLEM算法和MLEM互补算法在迭代次数n=5时对三种厚度编码板实测投影重建图像的NRMSE和CC值。由表 2可知，在编码板厚度相同的情况下，MLEM互补算法的NRMSE和CC值皆优于传统的MLEM算法，实验结果与模拟结果相一致。与MLEM算法相比，采用MLEM互补算法对编码图像进行重建，可以更有效地抑制噪声，提高重建图像的质量。

表 2

表 2 MLEM算法和MLEM互补算法的NRMSE、CC值 Table 2 NRMSE and CC of MLEM and complementary MLEM algorithm. d/mm NRMSE CC MLEM MLEM互补 Complementary MLEM MLEM MLEM互补 Complementary MLEM 10 83.07 41.01 0.03 0.05 20 52.87 17.29 0.06 0.09 30 49.02 15.61 0.07 0.11

表 2 MLEM算法和MLEM互补算法的NRMSE、CC值 Table 2 NRMSE and CC of MLEM and complementary MLEM algorithm.

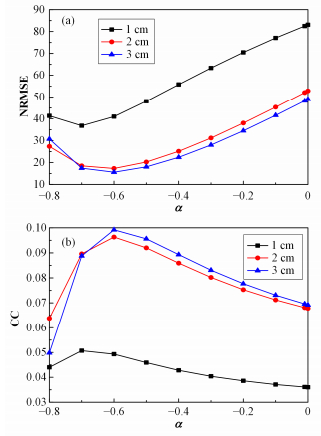
通过MLEM互补算法对上述实验及模拟投影数据进行重建时，α=-0.6。为研究不同α值对MLEM互补算法重建效果的影响，选取不同α值对实验所得厚度d=10mm、d=20mm、d=30mm三种厚度编码板的实测投影值进行互补MLEM算法重建。图 5为三种厚度下互补MLEM算法的NRMSE和CC值随修正因子α值的变化。

图 5

图 5 三种厚度铅制编码板NRMSE (a)和CC (b)值随α变化 Figure 5 NRMSE (a) and CC (b) for coded aperture in three thicknessesvs. α.

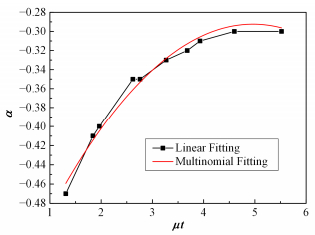
由图 5可知，随着α值在(-0.8, 0)区间内不断增大，重建图像的质量先随之提高，当α达到某一特定值后，重建图像的质量开始下降。对于MLEM算法存在最佳α值，使得改进后MLEM算法效果最优。编码板厚度为1 cm、2 cm、3 cm时，最佳α值分别为-0.7、-0.61、-0.55。可见随着编码板准直器厚度的增加，MLEM互补算法修正因子α的最佳值逐渐减小，最佳α值的选取与物质阻止本领有关。由γ射线在物质中的衰减规律$I = {I_0} \times {{\text{e}}^{-\mu t}}$，采用上述编码板模型，模拟不同μt值下，算法最佳α值的变化。图 6为最佳α值随μt的变化。由图 6可知，最佳α值随μt值一同增加，当μt值达到某一特定值时，α值的变化趋于平缓。计算所得α-μt拟合公式为：

图 6

图 6 最佳α值随μt值变化拟合曲线 Figure 6 Fitted curve of α-μt.

表 3为三种厚度下铅制编码板实测投影数据所得最佳α值与模拟数据拟合公式计算所得最佳α值。

表 3

表 3 三种厚度铅制编码板实验及模拟数据最佳α值 Table 3 Optimal α for three thicknesses of plumbous coded aperture by experiment and Monte Carlo simulation. 编码板厚度 Thickness of coded aperture/cm 实验值 Experiment value 模拟值 Simulation value 实验值/模拟值 Experimental value/simulative value 1 -0.70 -0.45 1.50 2 -0.61 -0.35 1.74 3 -0.55 -0.31 1.76

表 3 三种厚度铅制编码板实验及模拟数据最佳α值 Table 3 Optimal α for three thicknesses of plumbous coded aperture by experiment and Monte Carlo simulation.

由表 3可知，由于噪声影响，实验数据所得α值比模拟数据所得的要大。无法通过模拟数据所得α-μt拟合公式直接给出实测情况下MLEM互补算法最佳α值。在使用α-μt拟合公式给出实际成像系统所需最佳α值时，需对模拟所得最佳α值乘以相应比例系数。

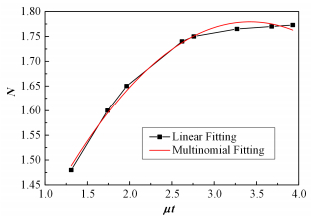
记α实验值与α模拟值的比值N为比例系数，根据α-μt拟合公式变化趋势，对N随μt值变化进行拟合。图 7为比例系数N随μt值的变化。

图 7

图 7 比例系数N随最佳μt值变化拟合曲线 Figure 7 Fitted curve of N-μt.

计算所得N-μt拟合公式为：

在求MLEM互补算法的最佳α值时，可以通过模拟所得α-μt拟合公式计算结果乘以N得到。

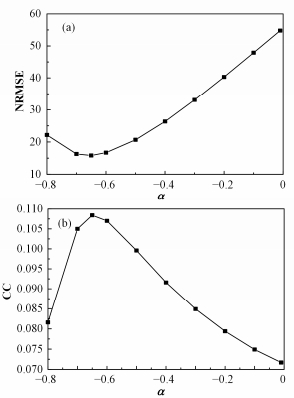
为验证上述结论，采用1cm钨板进行实验，图 8为钨板的NRMSE和CC值随α值的变化。由图 8可知，此时MLEM互补算法最佳α值为0.65。在入射γ射线能量为662keV时，钨的线性衰减系数μ=1.84cm^-1[10]；将t=1cm带入拟合公式(6)，得出模拟情况下算法最佳α值为0.41，由拟合公式(7)，此时N为1.6。最终用于1cm钨制编码板的最佳α=1.6×0.41=0.65。与实验测得数据所得最佳α值相一致。在实际应用中，可以用上述方法确定MLEM互补算法最佳α值。

图 8

图 8 1cm厚钨制编码板NRMSE (a)和CC (b)值随α变化 Figure 8 NRMSE (a) and CC (b) for 1-cm tungsten sheet thickness vs. α.

实验证明，将互补编码板相减去噪思想应用于MLEM算法中是可行的。通过对蒙特卡罗模拟所得投影数据及实测所得投影数据的重建结果可知，相比于MLEM算法，在编码板成像中，MLEM互补算法可以有效抑制噪声的影响，提高图像重建质量；MLEM互补算法中的α最佳值的选取与μt有关；通过模拟得出α-μt拟合公式所得模拟最佳α值与N-μt拟合公式所得N的乘积，可以得到实测数据的最佳α值，模拟结果与实验结果相一致。采用该方法可以确定MLEM互补算法最佳α值；在编码板成像系统中，采用蒙特卡罗模拟方法对其进行分析具有一定的可行性。