反应堆材料受到高通量中子辐照时,将产生微观与宏观尺度的结构损伤,导致其性能发生改变,因此开发耐辐照损伤的核材料成为研究热点[1-5]。粒子辐照首先在材料微观结构诱发点缺陷(空位/原子对),再通过空位聚集而形成较大空穴、空洞,导致材料变脆,从而造成材料性能退化甚至失效[6-7]。由于中子辐照实验条件及防护要求的限制,目前较难通过实验方法观察核材料的点缺陷产生与演化过程。因此,研究人员广泛利用计算机模拟手段进行研究。特别是分子动力学方法,已广泛用于模拟材料微观尺度点缺陷的产生与演化过程[8-14],为判断材料的辐照损伤机制及筛选耐辐照材料提供理论依据。
分子动力学模拟时,通常在结构模型中对某一原子赋予一定动能,假定其为入射中子碰撞所激发,即初级撞出原子(Primary Knock-on Atom, PKA)[15-16]。该PKA具有较大动能,使大量原子发生碰撞,引发级联效应(Effect of Collision Cascade, ECC)。级联效应导致原子发生位移,产生空位原子对,形成若干点缺陷[17-20]。此外,分子动力学可观察点缺陷的演化过程。由于PKA是级联效应的根源,故其初始条件的设定对分子动力学模拟有很大影响。分子动力学不能模拟PKA的产生过程,并缺乏相应核数据,因此目前对PKA的初始条件设定一般进行简化,易产生两个问题:1)如何合理地设定PKA能量;2) PKA的初始运动方向对级联效应有很大影响,包括碰撞次数、传递能量、运动路径等。此外,为方便模拟,一般会简化结构模型。例如,建立纯Fe的结构模型[21-23],以近似模拟各种钢材的辐照损伤机制。该简化处理的可靠性需进行论证。
1 模拟方法中子辐照材料时,与靶材原子发生碰撞,使其发生位移,成为具有一定动能的反冲原子。在核反应堆中,可产生能量较高的快中子。如裂变堆中,中子能量可达2MeV,在设计的聚变堆中,中子能量可达14MeV。当高能中子辐照核材料时,与靶材原子的相互作用较为复杂,除弹性散射和非弹性散射之外,还会发生核反应[24],如(n, n)、(n, xn)反应等,产生的次级中子对PKA类型、能谱等造成影响;另外,带电粒子反应如(n, p)、(n, He)等,不仅对PKA能谱产生影响,而且使靶核原子在离位时发生嬗变。因此,需要一种较精确的模拟软件对高能中子辐照产生的PKA进行追踪,以便更精确得到PKA的相关数据。
GEANT4是欧洲粒子中心开发的基于蒙特卡罗方法的开源程序包,可模拟不同粒子(如中子)的输运过程,能准确探测和追踪PKA原子[25-26]。通过材料成分、密度及三维尺寸的设定,可建立材料的几何模型。再设定中子能量及出射方向,从而实现粒子输运。中子能量范围从250eV到几个TeV,能覆盖裂变堆甚至聚变堆的中子能量范围。此外,GEANT4程序不仅能探测并记录入射中子与靶原子直接作用产生的PKA粒子,还能追踪各种中子核反应产生的次级粒子及间接产生的PKA粒子。为追踪PKA粒子的运动规律及获得相关数据,在GEANT4中编入若干新函数进行计算。
本工作选用105个能量分别为0.1MeV、0.3MeV、0.5MeV、0.7MeV、1MeV、2MeV、3MeV、4MeV、5MeV、6MeV、7MeV、8MeV、9MeV、10MeV、11MeV、12MeV、13MeV和14MeV的中子进行模拟。Zr基合金是一种应用较为广泛的核材料(如Zr-2和Zr-4)[27],因此选择纯Zr建立结构模型。作为对照,两种二元合金Zr2Cu和Zr2Ni也进行模拟。为获得具有足够统计意义的PKA数量,沿着中子入射方向,将靶材厚度设置为2cm。
2 结果与讨论 2.1 对PKA的初始动能优化中子不带电荷,不存在与原子的库仑作用,只考虑中子与原子核的作用,因而中子在材料中穿透性强。分子动力学模拟时,由于目前计算能力的限制,建立的结构模型一般仅包含几万到几十万原子,其一维尺寸不到微米量级[13]。由于模型体积小,因此入射粒子在模型内连续激发PKA的可能性很小。通常认为只能激发一个PKA粒子,因此,需预先设置PKA粒子动能。
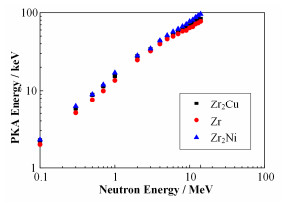
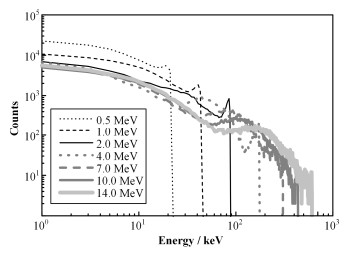
通过GEANT4模拟中子输运过程,可追踪所有PKA的产生过程及相关信息。图 1显示不同能量入射中子分别在Zr、Zr2Cu和Zr2Ni中产生的PKA平均能谱。可观察到,PKA平均能量随入射中子能量增大。如中子能量为1MeV时,PKA平均能量约为15keV;中子能量为14MeV时,PKA平均能量在80-90keV之间。图 2表示不同能量入射中子在纯Zr中产生的PKA能谱(Zr2Cu和Zr2Ni的PKA能谱图与Zr相似,未列出)。从理论而言,只要PKA能量在图 2能谱范围内,均可作为分子动力学模拟的PKA初始动能,但仍需进一步探讨如何合理设定PKA初始动能。比如,在众多的分子动力学模拟工作中,通常将PKA能量设置为几个keV,以模拟级联效应[13]。但从本文数据可知,裂变堆甚至聚变堆中所产生的PKA能量有较大概率达到几十甚至几百keV,因此,进行分子动力学模拟核材料时,研究初始动能为几十甚至几百keV的PKA粒子依然具有重要的研究意义。
|
图 1 不同能量入射中子产生的平均PKA能量 Figure 1 Average PKA energies produced by incident neutrons with different energies. |
|
图 2 不同能量入射中子在纯Zr中产生的PKA能谱 Figure 2 PKAs spectra in pure zirconium produced by incident neutrons with different energies. |
此外,从图 2可知,当入射中子能量一定时,产生的PKA能量有一个截断值。如入射中子能量分别为1MeV和14MeV时,PKA能量的截断值约为46keV和600keV。根据能量守恒公式[28]:
| $ E = \frac{{4{M_{\rm{n}}}M}}{{{{({M_{\rm{n}}} + M)}^2}}}{E_{\rm{n}}}{\cos ^2}\theta $ | (1) |
式中:Mn表示中子质量;M为靶核质量;En为入射中子能量;q为反冲原子出射角度。由式(1)可知,当入射中子能量一定、q为0°时,中子与原子核发生对心碰撞,靶原子获得最大能量。例如,入射中子能量为1MeV时,反冲原子的最大能量为43keV;入射中子能量为14MeV时,反冲核最大能量为602keV。图 2所示截断值与式(1)的推导数值吻合,证明了本模拟工作的可靠性。
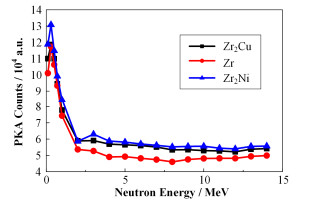
对于核裂变堆甚至聚变反应堆,其核材料多选用各种合金材料,如锆基合金和铁基合金(各种钢材)。在合金中,除了主体元素,通常也包含多种其他元素,甚至微量元素,以调节和优化性能,但结构变得较为复杂,因此进行分子动力学研究时,合金材料很难进行建模,通常选用对应的简单结构模型进行近似模拟(如用纯Fe模型近似各种钢材)。由图 1、2可知,Zr与Zr2Cu和Zr2Ni两种二元合金成分相比,中子辐照产生的PKA能谱比较接近。图 3为PKA数量对应入射中子能量的分布。如图 3所示,入射中子能量一定时,三种材料中产生的PKA数量非常接近。进一步可推断,入射中子能量一定时,三种材料中的辐照损伤相当。因此利用分子动力学进行模拟时,可用纯Zr结构模型代替Zr2Cu和Zr2Ni。在Zr2Cu和Zr2Ni中,Zr含量为67%,而对于Zr-2和Zr-4核材料,其Zr含量可达98%,近似于纯Zr[27],故而可推断,当中子辐照Zr-2和Zr-4时,其PKA能谱以及PKA数目应与纯Zr结果非常接近。因此,虽然不能直接利用分子动力学模拟Zr-2和Zr-4的中子辐照损伤,但可通过模拟纯Zr模型进行近似研究。进一步推论,对于包含多种成分和结构较复杂的各种合金材料,可通过模拟其对应的简单结构模型获得近似结果。
|
图 3 不同能量入射中子分别在Zr2Cu、Zr、Zr2Ni中产生的PKA计数分布 Figure 3 Distribution of PKA counts produced by incident neutrons with different energies in Zr2Cu, Zr and Zr2Ni. |
在分子动力学研究中,为方便计算,PKA速度方向通常定为垂直于晶界方向,而晶界一般设置为平行模型表面或某一特殊晶面,即PKA方向简化为平行某一晶面甚至模型表面。构建结构模型时,由于所含原子一般不超过几十万,体量较小,只设置1-2个晶界。晶界通常被视为移位原子及剩余空位的吸收区。在PKA诱发级联效应时,PKA与晶界的距离和方向对模拟结果影响很大,尤其影响碰撞次数、传递能量和移位原子的运动路径[13]。因此,研究PKA速度方向对分子动力学模拟具有重要意义。
通过GEANT4模拟中子输运过程,可追踪任一由中子辐照产生的PKA粒子。在程序设定中,将中子入射方向设为与材料表面平行,将PKA散射角定义为PKA速度方向与中子入射方向之间的夹角。
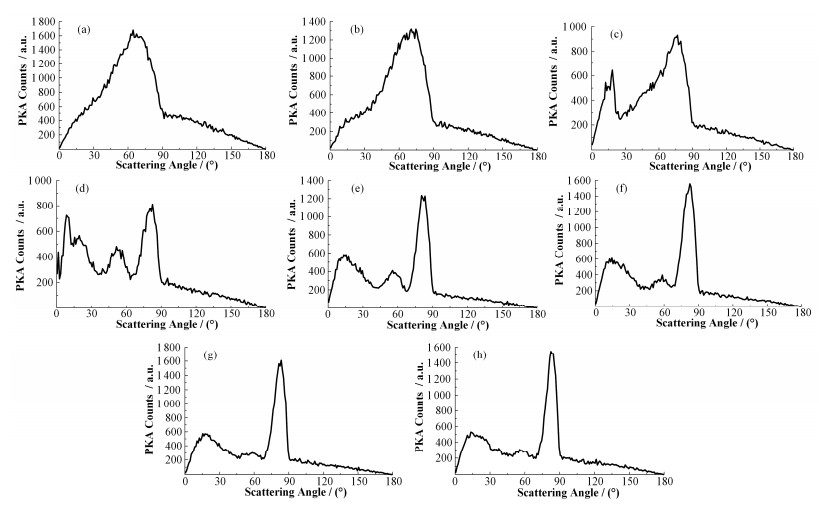
图 4为不同能量入射中子产生的PKA的散射角分布,表 1为图 4峰值处的弹性散射与非弹性散射贡献的PKA数目。由图 4(a-b)可知,当入射中子能量较低时,出现一个明显强峰,表明此时PKA在70°左右具有最可能的出射角度,源于此时弹性散射计数高(如表 1所示)。此外,分布在0°-90°的PKA明显多于90°-180°的PKA。由弹性碰撞理论[28]与表 1数据可知,入射中子与靶原子核发生初次弹性散射时,产生的PKA散射角分布在0°-90°之间;当中子一次碰撞后偏离原入射方向,再次与靶原子发生二次甚至多次碰撞时,产生的PKA散射角分布于整个0°-180°区间。而发生初次碰撞的几率大于二次及多次碰撞,故综合而言,碰撞效应主要贡献于0°-90°区间。如图 4(c-f)所示,当中子能量较高时,除了82°最强峰以外,在18°和52°出现两个强峰。
| 表 1 入射中子数为105时散射角峰值处弹性散射与非弹性散射的PKA数值 Table 1 Counts of both inelastic and elastic scattering corresponding to the peaks of scattering angles of PKAs when the number of incident neutrons is 105. |
由表 1可知,当入射中子能量较高时,可与靶材原子发生核反应,如(n, n')和(n, 2n)等,产生的PKA会导致18°出现强峰。该结果表明,此时PKA最可能出射方向对应于18°、52°和82°三个角度。当入射中子能量很大时,由图 4(g-h)和表 1可知,52°峰的强度会逐渐降低,源于此时弹性和非弹性散射沿该角度产生PKA概率降低,而更倾向于18°和82°散射角出射。综上,可获得在不同能量中子入射时,对应的PKA最优出射角度,有助于指导分子动力学模拟的PKA速度方向设定。例如,模拟裂变堆核材料的辐照效应时,主要考虑低于2MeV中子所导致的PKA,其散射角度定为70°左右为宜;当模拟裂变堆核材料的辐照效应时,需考虑典型的14MeV中子问题,则PKA的散射角度设置为18°和82°为宜。
|
图 4 不同能量入射中子产生的PKA散射角分布(a) 0.5MeV,(b) 1MeV,(c) 2MeV,(d) 4MeV,(e) 7MeV,(f) 9MeV,(g) 12MeV,(h) 14MeV Figure 4 Scattering angles distributions of PKA caused by incident neutrons with different energies. (a) 0.5MeV, (b) 1MeV, (c) 2MeV, (d) 4MeV, (e) 7MeV, (f) 9MeV, (g) 12MeV, (h) 14MeV |
对于分子动力学模拟材料的粒子辐照效应,优化其初始条件及验证其结构模型的选取至关重要。本文采用GEANT4模拟三种Zr基材料的中子输运过程,获得了对应的PKA信息,可解决上述问题。结果表明,高能入射中子辐照Zr基材料时,产生的PKA最高能量达几十甚至几百keV;在不同Zr材料中产生的PKA数量比较接近,形成的PKA能谱也非常相似,因此可证实,进行分子动力学模拟材料辐照效应时,采用简化的结构模型进行近似处理是可行的;此外,本文对中子辐照产生的PKA散射角进行了计算,评估了不同能量入射中子产生PKA的最佳散射角。上述研究结果对于核材料,尤其是裂变堆和聚变堆核材料的模拟计算工作具有重要参考价值。
| [1] | Mansur L K, Rowcliffe A F, Nanstad R K, et al. Materials needs for fusion, generation IV fission reactors and spallation neutron sources-similarities and differences[J]. Journal of Nuclear Materials, 2004, 329-333(Part A): 166–172. DOI: 10.1016/j.jnucmat.2004.04.016 |
| [2] | Yvon P, Carre F. Structural materials challenges for advanced reactor systems[J]. Journal of Nuclear Materials, 2009, 385(2): 217–222. DOI: 10.1016/j.jnucmat.2008.11.026 |
| [3] | Zinkle S J, Busby J T. Structural materials for fission & fusion energy[J]. Materials Today, 2009, 12(11): 12–19. DOI: 10.1016/S1369-7021(09)70294-9 |
| [4] |
白新德, 王社管, 马春来, 等. 离子轰击模拟中子辐照在核材料研究中的应用[J].
原子能科学技术, 1996, 30(5): 469–474.
BAI Xinde, WANG Sheguan, MA Chunlai, et al. Application of simulation of neutron irradiation by ion bombardment in nuclear material research[J]. Atomic Energy Science and Technology, 1996, 30(5): 469–474. |
| [5] | Zinkle S J, Was G S. Materials challenges in nuclear energy[J]. Acta Materials, 2013, 61(3): 735–758. DOI: 10.1016/j.actamat.2012.11.004 |
| [6] | Wirth B D. How dose radiation damage materials?[J]. Science, 2007, 318(5852): 923–924. DOI: 10.1126/science.1150394 |
| [7] | Sickafus K E, Kotomin E A, Uberuaga B P. Radiation effects in solid, NATO science series II: mathematic, physics and chemistry[M]. Amsterdam: Springer Press, 2007. |
| [8] | Nordlund K, Gao F. Formation of stacking-fault tetrahedra in collision cascades[J]. Applied Physics Letters, 1999, 74(18): 2720–2722. DOI: 10.1063/1.123948 |
| [9] | Bacon D J, Gao F, Osetsky Y N. The primary damage state in fcc, bcc and hcp metals as seen in molecular dynamics simulations[J]. Journal of Nuclear Materials, 2000, 276(1-3): 1–12. DOI: 10.1016/S0022-3115(99)00165-8 |
| [10] |
贺新福, 杨鹏, 杨文. Fe-Cu合金基体损伤的分子动力学模拟研究[J].
金属学报, 2011, 47(7): 954–957.
HE Xinfu, YANG Peng, YANG Wen. Molecular dynamics simulation of matrix radiation damage in Fe-Cu alloy[J]. Acta Metallurgica Sinica, 2011, 47(7): 954–957. DOI: 10.3724/SP.J.1037.2011.00207 |
| [11] | Soneda N, Diaz R T. Defect production, annealing kinetics and damage evolution in α-Fe: an atomic-scale computer simulation[J]. Philosophical Magazine A, 2009, 78(5): 995–1019. DOI: 10.1080/01418619808239970 |
| [12] |
王建伟, 尚新春, 吕国才. bcc-Fe空位浓度对辐照损伤影响的分子动力学模拟[J].
材料工程, 2011, 10: 15–18.
WANG Jianwei, SHANG Xinchun, LYU Guocai. Molecular dynamics simulation of vacancy concentration on irradiation cascades damage effects in bcc-Fe[J]. Journal of Materials Engineering, 2011, 10: 15–18. |
| [13] | Bai X M, Voter A F, Hoagland R G, et al. Efficient annealing of radiation damage near grain boundaries via interstitial emission[J]. Science, 2010, 327(5973): 1631–1634. DOI: 10.1126/science.1183723 |
| [14] | Bacon D J, Calder A F, Gao F. Defect production due to displacement cascades in metals as revealed by computer simulation[J]. Journal of Nuclear Materials, 1997, 251: 1–12. DOI: 10.1016/S0022-3115(97)00216-X |
| [15] |
马佳文, 巩文斌, 张伟, 等. 内嵌金属的多壁碳纳米管辐射损伤研究[J].
核技术, 2016, 39(6): 060503.
MA Jiawen, GONG Wenbin, ZHANG Wei, et al. Theoretical study on irradiation damage of metal-filled multi-walled carbon nanotubes[J]. Nuclear Techniques, 2016, 39(6): 060503. DOI: 10.11889/j.0253-3219.2016.hjs.39.060503 |
| [16] | Calder A F, Bacon D J, Barashev A V, et al. Effect of mass of the primary knock-on atom on displacement cascade debris in alpha-iron[J]. Philosophical Magazine Letters, 2008, 88(1): 43–53. DOI: 10.1080/09500830701733004 |
| [17] |
李融武, 潘正瑛. 聚变α粒子对材料辐照损伤瞬时行为的研究[J].
核技术, 1995, 18(4): 203–208.
LI Rongwu, PAN Zhengying. Temporal development of radiation damage caused by fusion α-particles[J]. Nuclear Techniques, 1995, 18(4): 203–208. |
| [18] | Nordlund K, Ghaly M, Averback R S, et al. Defect production in collision cascades in elemental semiconductors and fcc metal[J]. Physical Review B, 1998, 57(13): 7556–7570. DOI: 10.1103/PhysRevB.57.7556 |
| [19] |
吕铮, 刘春明. 快中子反应堆核心结构材料的辐照损伤[J].
材料与冶金学报, 2011, 10(3): 203–208.
LYU Zheng, LIU Chunming. Irradiation damage of structural materials for fast reactor application[J]. Journal of Materials and Metallurgy, 2011, 10(3): 203–208. DOI: 10.14186/j.cnki.1671-6620.2011.03.002 |
| [20] | Gilbert M R, Dudarev S L, Derlet P M, et al. Structure and metastability of mesoscopic vacancy and interstitial loop defects in iron and tungsten[J]. Journal of Physics: Condensed Matter, 2008, 20(34): 345214. DOI: 10.1088/0953-8984/20/34/345214 |
| [21] | Terentyev D A, Malerba L, Chakarova R, et al. Displacement cascades in Fe-Cr: a molecular dynamics study[J]. Journal of Nuclear Materials, 2006, 349(1-2): 119–132. DOI: 10.1016/j.jnucmat.2005.10.013 |
| [22] | Becquart C S, Domain C, van Duysen J C, et al. The role of Cu in displacement cascades examined by molecular dynamics[J]. Journal of Nuclear Materials, 2001, 294(3): 274–287. DOI: 10.1016/S0022-3115(01)00421-4 |
| [23] | Malerba L, Terentyev D, Olsson P, et al. Molecular dynamics simulation of displacement cascades in Fe-Cr alloys[J]. Journal of Nuclear Materials, 2004, 329-333(Part B): 1156–1160. DOI: 10.1016/j.jnucmat.2004.04.270 |
| [24] | Gilbert M R, Marian J, Sublet J C. Energy spectra of primary knock-on atoms under neutron irradiation[J]. Journal of Nuclear Materials, 2015, 467(Part 1): 121–134. DOI: 10.1016/j.jnucmat.2015.09.023 |
| [25] | Agostinelli S, Allison J, Amako K, et al. Geant4-a simulation toolkit[J]. Nuclear Instruments and Methods in Physics Research Section A, 2003, 506(3): 250–303. DOI: 10.1016/S0168-9002(03)01368-8 |
| [26] | Apostolakis J, Asai M, Bogdanov A G, et al. Geometry and physics of the Geant4 toolkit for high and medium energy applications[J]. Radiation Physics and Chemistry, 2009, 78(10): 859–873. DOI: 10.1016/j.radphyschem.2009.04.026 |
| [27] |
王旭峰, 李中奎, 周军, 等. Zr合金在核工业中的应用及研究进展[J].
热加工工艺, 2012, 41(2): 71–74.
WANG Xufeng, LI Zhongkui, ZHOU Jun, et al. Application and research progress of zirconium alloy in nuclear industry[J]. Hot Working Technology, 2012, 41(2): 71–74. DOI: 10.3969/j.issn.1001-3814.2012.02.021 |
| [28] |
杨朝文.
电离辐射防护与安全基础[M]. 北京: 原子能出版社, 2009: 1-215.
YANG Chaowen. Ionizing radiation protection and safety[M]. Beijing: Atomic Energy Publishing House, 2009: 1-215. |


