超临界水冷堆(Supercritical Water-cooled Reactor, SCWR)作为第四代反应堆中唯一的水冷堆，堆芯工作压力25MPa，出口冷却剂温度500℃左右，具有经济性好、系统简单和可持续性强等诸多优势^[1-2]。SCWR的热工水力过程是研究超临界水堆的关键环节，直接关系到反应堆安全性和经济性。随着超临界水传热和流动研究的发展，国内外诸多学者在超临界水传热关系式方面开展了大量工作^[3-8]。Bishop等^[3]研究了近临界温度和超临界压力下的强迫对流换热关系式；Watts等^[4]研究了竖直通道内超临界水核热耦合瞬态工况传热关系式；陈玮玮等^[8]通过对大量实验数据的分类对比对超临界水竖直管内传热关系式计算的精度进行了研究。这些关系式在各自的实验条件下与实验符合良好，但是，随着工况的变化，出现了不同程度的误差。因此，针对实际工况选择合适的关系式，可以提高实际计算的准确度，减小计算误差。在影响换热的因素中，每一种因素会因其所处的条件差异表现出不同的特征，其中的关系较为复杂，不易确定，具有一定的模糊性。换热关系式的选择是依据各影响因素的标准，判断实际工况与哪个换热关系式标准最接近，则认为该工况最符合这个关系式。模糊贴近度是模糊数学中的一种比较实用的方法^[9]，用来描述两个模糊集的贴近程度。它已成功地在水环境质量评价、土壤环境评价中得到广泛应用^[10-11]。以现有存在的传热关系式为基础，借助模糊数学中贴近度的概念，通过比较与各个经验公式适用范围的贴近程度，找到了实际工况下最为适用的经验关系式，可以减少计算误差。

贴近度^[9]是用来度量两个模糊集接近程度的数量指标，式(1)-(6)给出其定义。

设映射$T:F(X)\times F(X)\to [0, 1]$满足：对于A、B、C、F(X)，

称T为F(X)上的贴近度函数；T(A,B)为A和B的贴近度。常见的贴近度有：Hamming贴近度、Euclid贴近度、最大最小贴近度如式(4)-(6)所示。

若$X=\{{{x}_{1}}, {{x}_{2}}, {{x}_{3}}, ..., {{x}_{n}}\}$，A,B∈F(X)则：

Hamming贴近度：

Euclid贴近度：

最大最小贴近度：

为了更好地比较不同取值范围间向量的差异，计算前通过式(7)-(8)对数据进行归一化，使其位于[0, 1]之间。

式中：$ i=1, 2, \ldots, n $；$ a=\max x $；$ b=\max y $。

由于每个影响因素对结果影响大小不同，需要考虑各影响因素的权重问题。权重系数的确定方法一般有层次分析法和变异系数法等，研究采用变异系数法来确定影响因素的权重指标^[12-13]。变异系数法认为某个影响因素数值之间的差异性越大，则该指标在综合评价中的作用越大，其权重也越大。所以，根据各个影响因素数值之间的差异性，利用变异系数这个参数来确定各影响因素的权重。变异系数法计算权重如式(9)、(10)所示。

式中：V_i是第i项指标的变异系数；σ_i是第i项指标的标准差；$ \overline{{{x}_{i}}} $是第i项指标的平均数；W_i是各项指标归一化后的权重。

模糊数学中择近原则^[9]是模糊识别的一种常用方法，贴近度是它的基础。通过已知模式的贴近度与待识别对象比较，如果该识别对象的贴近度最大，那么它就属于该模式。设${{A}_{1}}, {{A}_{2}}, {{A}_{3}}, ..., {{A}_{n}}$是论域U上的n个模糊子集，B也是U上的模糊子集，若：

则判断B与$ {{A}_{i0}} $为同一类，或者说B是$ {{A}_{i0}} $。

由于每个实验关联式都在一定实验范围内得出，因此，他们都有其相应的使用范围。为了便于关系式的选择，表 1列出部分适用于超临界水的主要换热关系式^[3-7]的适用范围。Nu为努塞尔数；Re为雷诺数；Pr为普朗特数；b为主流流体；w为壁面；μ为粘性系数，Pa·s。

表 1

表 1 各关系式适用范围 Table 1 Applicability of relations 关系式名称 Relational expression 关联式 Relation 压力 Pressure / MPa 质量流密度 Mass flow density/ kg·m−2·s−1 热流密度 Heat flux density / kW·m−2 Bishop $Nu=0.006\ 9R{{e}^{0.9}}{{\overline{Pr}}^{0.66}}{{\left( \frac{{{\rho }_{\text{w}}}}{{{\rho }_{\text{b}}}} \right)}^{0.43}}\left( 1+2.4\frac{D}{x} \right)$ 22.8-27.6 651-3662 310-3460 Watts $Nu=0.021R{{e}^{0.8}}{{\overline{Pr}}^{0.55}}{{\left( \frac{{{\rho }_{\text{w}}}}{{{\rho }_{\text{b}}}} \right)}^{0.35}}\phi $ 25.0 130-1000 170-450 Yamagata $ Nu=0.013\ 5R{{e}^{0.85}}P{{r}^{0.8}}\cdot Fc $ 22.6-29.4 310-1830 116-930 Shitsman $Nu=0.023R{{e}^{0.8}}P{{r}_{\min }}^{0.8}$ 24.5-34.3 350-600 270-700 Swenson $\frac{hD}{{{k}_{w}}}=0.004\ 59{{\left( \frac{DG}{{{\mu }_{w}}} \right)}^{0.923}}{{\left( \frac{({{H}_{w}}-{{H}_{b}}){{\mu }_{w}}}{({{T}_{w}}-{{T}_{b}})} \right)}^{0.613}}\times {{\left( \frac{{{\rho }_{w}}}{{{\rho }_{b}}} \right)}^{0.231}}$ 23.0-41.0 542-2150 200-1800

表 1 各关系式适用范围 Table 1 Applicability of relations

基于§1.2中的选择原则，进行换热关系式选择，计算流程如下：

1) 建立评价标准及整理样本：根据选择的不同换热关系式的适用范围，确定各关系式的特征指标。

2) 样本数据归一化：使计算结果方便、准确，对样本进行归一化处理。

3) 权重系数矩阵确定：压力(p, MPa)、质量流密度(G, kg·m⁻²·s⁻¹)等影响因素对换热系数(h, W·m⁻²·k⁻¹)的影响程度不同，采用变异系数法进行权重计算。

4) 计算模糊贴近度：分别采用Hamming贴近度、Euclid贴近度、最大最小贴近度计算样本与各个关系式的贴近程度，对结果进行对比。

5) 确定待分类样本及验证：根据模糊择近原则，选择与样本贴近度最大的关系式进行计算。

根据现有的研究，超临界水换热系数的计算主要与压力、质量流密度、热流密度(Q)有关，选取这三个参量作为考核标准，根据贴近度定义^[9]描述某一点与某范围的贴近程度，则认为该点与区间中点越靠近，则越贴近区间；集本团队部分研究^[14-15]成果，选取表 1中参数中点作为换热关联式的参数指标如表 2所示。另外方便检验，选取Swenson等^[7]的实验数据作为待选定数据。

表 2

表 2 超临界水换热公式评价指标及待选定参数 Table 2 Evaluation index of supercritical water heat transfer formula and parameters to be selected. 关系式名称 Relational expression 压力 Pressure / MPa 质量流密度 Mass flow density/ kg·m−2·s−1 热流密度 Heat flux density/ kW·m−2 Bishop 25.200 2 156.5 1 885.0 Watts 25.000 565.00 310.00 Yamagata 26.000 1 070.0 523.00 Shitsman 29.400 475.00 485.00 Swenson 32.000 1 346.0 1 000.0 待选定 To be selected 31.000 2 150.0 789.00

表 2 超临界水换热公式评价指标及待选定参数 Table 2 Evaluation index of supercritical water heat transfer formula and parameters to be selected.

为了更好地比较不同取值范围间向量的差异，计算前采用式(8)对表 2中数据进行归一化，使其位于[0, 1]之间。计算结果如表 3所示。表 2与表 3意义相同。

表 3

表 3 归一化后超临界水换热公式评价指标及待选定参数 Table 3 Evaluation index of the normalized supercritical water heat transfer formula and the parameters to be selected. 关系式名称 Relational expression 压力 Pressure/ MPa 质量流密度 Mass flow density/ kg·m−2·s−1 热流密度 Heat flux density/ kW·m−2 Bishop 0.788 1.000 1.000 Watts 0.781 0.262 0.164 Yamagata 0.813 0.496 0.277 Shitsman 0.919 0.220 0.257 Swenson 1.000 0.624 0.530 待选定 To be selected 0.969 0.997 0.419

表 3 归一化后超临界水换热公式评价指标及待选定参数 Table 3 Evaluation index of the normalized supercritical water heat transfer formula and the parameters to be selected.

由于每个因素影响换热系数的程度不相同，采用式(9)、(10)计算表 3中的数据得到各影响因素权重：压力为0.1，质量流密度为0.4，热流密度为0.5。

根据表 3中的数据及各影响因素权重，分别采用式(4)-(6)计算Hamming贴近度、Euclid贴近度、最大最小贴近度结果如表 4所示。

表 4

表 4 不同贴近度计算值 Table 4 Calculated values of different closeness. Bishop Watts Yamagata Shitsman Swenson Hamming贴近度Hamming closeness 0.69 0.56 0.71 0.60 0.80 Euclid贴近度Euclid closeness 0.58 0.49 0.66 0.50 0.75 最大最小贴近度Maximum minimum closeness 0.69 0.38 0.61 0.50 0.74

表 4 不同贴近度计算值 Table 4 Calculated values of different closeness.

从表 4可知，采用Hamming贴近度、Euclid贴近度计算结果一致，由好到差的顺序为：Swenson、Yamagata、Bishop、Shitsman和Watts公式。最大最小贴近度计算结果由好到差的顺序为：Swenson、Bishop、Yamagata、Shitsman和Watts公式；但Bishop和Yamagata公式计算结果大小接近。

引入平均绝对误差(Mean Absolute Deviation, MAD) D_MA、平均相对误差(Mean Relative Deviation, MRD) D_MR、标准偏差(Standard Deviation, SD) D_S来评价Swenson换热公式。

式中：D_MA表示公式计算值与实验值之间差距的大小；D_S表示公式计算值偏离算数平均值程度的大小，D_S越小，表示这些数值偏离平均值的程度越小，反之则偏离平均值的程度越大。Swenson换热公式的平均绝对相对误差D_MA=12.8%、标准偏差D_S=3.01%。

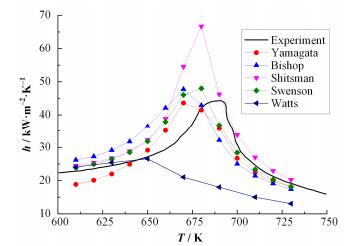
通过表 1中的换热关系式计算，得出换热系数随主流温度的变化情况，并与Swenson实验数据^[7]进行比较，结果如图 1所示。

图 1

图 1 各关系式计算的换热系数随主流温度T的变化情况与实验值的比较 Figure 1 Variation of heat transfer coefficient with main flow temperature t and the comparison with experimental values.

从图 1中可知，以上5个换热关系式都可以预测出超临界水换热系数随着温度升高，出现先增大后减小的趋势。其中，Shitsman公式预测的换热系数比实验值高将近两倍。Watts公式预测结果偏低，且最大值出现位置提前。Bishop、Yamagata、Swenson公式预测效果较好。因此，在单一选用一种换热关联式进行计算时，在部分工况下与实验数据相比会出现较大偏差。贴近度计算就是针对不同工况，合理选择最符合的超临界换热关系式。

1) 借助模糊贴近度的概念，并引入变异系数法综合考虑各影响因素权重系数，以具体的工况为例采用Hamming贴近度、Euclid贴近度及最大最小贴近度三种贴近度对该工况计算，比较分析了超临界水换热公式选择的步骤，获得了较好的效果。

2) 模糊贴近度综合考虑了各因素对超临界水换热系数的影响，根据确定工况与各公式的贴近程度进行选择。该方法评价原理直观、计算方法简单，是一种实用而准确的评价方法，为超临界水堆的流动换热问题提供了一种可以在已知关联式的基础上，做出针对实际工况的最优关联式选择方法，使实际计算结果更加准确。

3) 模糊数学中贴近度在超临界水堆中的应用是一种新的途径，随着对流动换热问题的深入研究，实验关联式增多，这种方法越精确，所做的选择与实际越相符。模糊评价指标选定是后续工作研究的重点。下一步打算采用权值的办法进行修正即选择中点、左四分之一点及右四分之三点，针对不同的情况，进行不同的权值修正，以得到更为准确的模糊评价指标。对于研究适用范围广的换热关系式，该方法还存在一些不足，改善模糊评价指标、提高结果精确度是后续工作研究的主要问题。