2. 南方医科大学 广州 510515
2. Southern Medical University, Guangzhou 510515, China
放疗计划设计过程中由于患者体表弯曲导致剂量分布不均匀,这种情况通常需要利用楔形板对射线束进行修整,以获得剂量均匀分布。扩充型动态楔形板(Enhanced Dynamic Wedge, EDW)不但具有传统固定楔形板的功能,更具有其独特的优点,EDW能够提高靶区剂量的均匀性,同时降低正常组织的受照剂量,大大减少照射时间和跳数,提高工作效率[1]。EDW射野产生的剂量分布精度关系到病人的疗效,需要进行专门的质量保证[2],目前大部分放疗单位使用Matrixx二维电离室矩阵进行动态楔形板质量保证[3],本研究使用蒙特卡罗方法模拟瓦里安23EX直线加速器的EDW,首先采用BEAMnrc程序中的组件模块DYNJAWS来模拟EDW,生成EDW源模型,然后用DOSXYZnrc程序计算体模内剂量,并结合相同条件下实验测量结果分析楔形因子和离轴剂量分布曲线,对EDW模型进行验证,开发一个独立的EDW质量保证工具。
1 方法 1.1 EDW工作原理EDW是通过加速器独立准直器运动和剂量率变化来实现特定剂量分布。瓦里安系统为每一档能量的光子提供一套60°动态楔形板的Golden STT (Segmented Treatment Table)表,即最大野的加速器输出跳数(Monitor Unit, MU)对应Y准直器运动挡块位置的分配表。治疗过程中STT表控制准直器移动速度和剂量率,生成相应楔形角的EDW,用户设定照射野大小和楔形角度后,系统从已存储的Golden STT表中截取相应的一段数据,用它和相应开野按一定比例合成所需角度的楔形野,最后结合所给加速器MU数生成治疗用的STT表[4]。准直器运动坐标系统中静止准直器一边为正,准直器运动范围为-20-9.5 cm,运动准直器最后位置距离静止准直器0.5 cm。
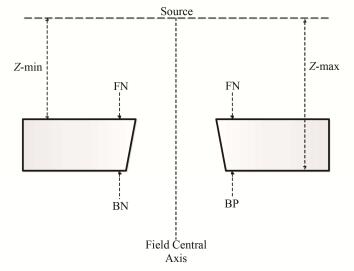
1.2 蒙特卡罗建模使用BEAMnrc模拟Varian23EX加速器6 MV光子束在二级准直器上方生成相空间平面[5],该相空间平面作为EDW模拟的输入源[6],使用BEAMnrc程序中的组件模块DYNJAWS模拟EDW,在之前的研究中Kakakhel等[7]基于BEAMnrc程序模拟EDW,实现了EDW输入文件的自动化,探讨了动态和静态两种模式的优劣。本研究直接使用更加精确的动态模式模拟EDW,在BEAMnrc模拟过程中需要读取包含EDW信息的输入文件。输入文件包括子野数量、子野概率、Y准直器坐标、Z-distance。Y准直器的坐标:前表面正坐标值(Front positive, FP)、后表面正坐标值(Back positive, BP)、前表面负坐标值(Front negative, FN)、后表面负坐标值(Back negative, BN),X准直器固定。Z-distance包括Z-min和Z-max,Z-min表示源到准直器前表面的距离;Z-max表示源到准直器后表面的距离,如图 1所示。
|
图 1 DYNJAWS坐标 Figure 1 Coordinate of DYNJAWS. |
子野概率用变量index描述,m1是0-1之间生成的随机数,如果index(i-1) < m1≤index(i),则使用第i个子野。动态模式中在第i个和i-1个子野之间进行插值,表达连续的准直器运动。选择一个子野的概率是基于STT表计算得到,STT表定义了准直器的位置和对应的剂量,根据能量、楔形角和射野大小截取相关的STT表,从机器dynalog file中读取准直器位置,与STT表中准直器的位置进行比较,如果匹配则使用STT表中的剂量值作为选择子野的概率;如果不匹配,则执行插值,确定当前子野的概率。在DYNJAWS模块中读取包含准直器信息的SEQUENCE文件,完成不同角度的EDW的蒙卡建模[8]。
BEAMnrc模拟含EDW的加速器机头生成的相空间平面距离源44.5 cm,该相空间文件作为DosXYZnrc的输入源文件,在DosXYZnrc程序的源选项中设置源到等中心距离(Distance from source to isocenter):55.5cm,最终源到体模表面的距离(Source Skin Distance, SSD)为100 cm。为提高计算效率,在BEAMnrc中设置电子截止能量ECUT= 0.70MeV,光子截止能量PCUT=0.01 MeV,电子射程截断能量ESAVE=2.0 MeV,采用方向韧致辐射分裂(Directional Bremsstrahlung Splitting, DBS)方差减少技术,轫致辐射粒子分裂数NBRSPL=1000,分裂野半径30 cm,在DOSXYZnrc中设置Ns=40。BEAMnrc模拟粒子数:5×108,DosXYZnrc模拟粒子数:5×108;剂量计算体模规格:30 cm×30 cm× 20cm;单一体素大小:0.2 cm×0.2 cm×0.2 cm。通过DosXYZnrc计算体模内的剂量,进而计算不同大小对称射野和非对称射野的楔形因子,获得10cm×10cm、20cm×20 cm射野,SSD 100 cm,水下10 cm处4个不同楔形角度的离轴剂量分布曲线和30°楔形角不同深度的离轴剂量分布曲线。
1.3 实验测量楔形因子是在相同位置,照射相同跳数,加和不加楔形板时射野中心轴上某一点剂量之比。楔形因子的测量条件:能量6 MV,SSD 100 cm。测量位置:射野中心轴水下10 cm处,测量对称射野5cm×5 cm到20 cm×20 cm加EDW和不加EDW的剂量。测量过程使用FC65指型电离室,用Dose1剂量仪接收测量数据,动态楔形板选择Y1-IN方向[9],电离室长轴垂直于楔形方向和射野中心轴[10]。非对称射野设计:在楔形方向Y2固定于10 cm位置,Y1为0-20 cm,非楔形方向X1:10 cm、X2:10 cm,测量点位于射野的几何中心Y0,Y0与Y1的位置关系如表 1所示。
| 表 1 准直器位置与射野中心的关系 Table 1 Relation of jaw position and field center. |
离轴Profiles测量条件:能量6 MV、SSD 100cm。射野大小:10 cm×10 cm、20 cm×20 cm,固体水下10 cm,动态楔形板选择Y2-OUT方向,用德国IBA (Ion Beam Applications)公司的Matrixx二维电离室矩阵(1020个电离室,电离室高:0.5 cm,直径:0.45 cm,0.08 cm3的灵敏体积)测量不同楔形角的离轴剂量分布[11-12]。
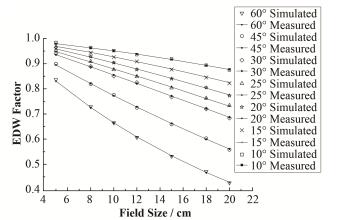
2 结果 2.1 对称射野的楔形因子对称射野的楔形因子如图 2所示,楔形因子随着射野大小增大而减小,10°-30°楔形板的楔形因子随着射野增大楔形因子减小的幅度较大,45°和60°楔形板的楔形因子随着射野增大楔形因子减小的幅度较小,5 cm×5 cm射野的楔形因子蒙特卡罗模拟值普遍大于测量值,模拟值与测量值平均偏差小于1%。
|
图 2 对称射野的楔形因子 Figure 2 EDW factor of symmetric fields. |
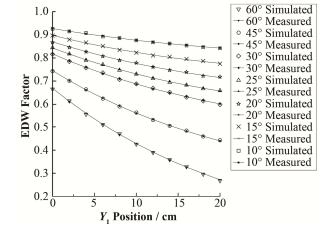
非对称射野的楔形因子如图 3所示,非对称射野的测量点位于射野几何中心Y0,根据表 1准直器Y1在坐标原点处,对应的测量点Y0位于Y轴的5 cm处,非对称射野的楔形因子随着Y1准直器的增大而减小,并且减小的幅度变小,模拟值与测量值平均偏差小于1%。
|
图 3 非对称射野的楔形因子 Figure 3 EDW factor of asymmetric fields. |
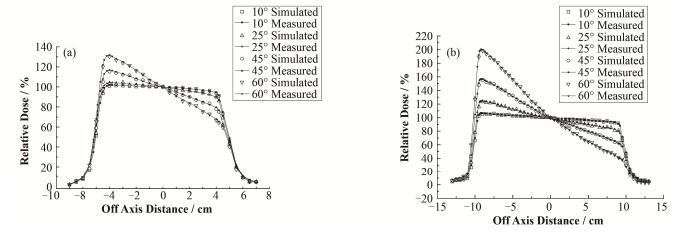
对比10 cm×10 cm、20 cm×20 cm的射野在水下10 cm处10°、25°、45°、60°楔形角的离轴剂量分布曲线,结果如图 4所示,模拟值和测量值取得了很好的一致,偏差小于2%,在高剂量区模拟值微低于测量值。相对剂量曲线以射野中心点的剂量归一,其中蒙特卡罗剂量计算的误差小于1%。
|
图 4 不同角度EDW离轴剂量分布曲线 (a) 10 cm×10 cm,(b) 20 cm×20 cm Figure 4 Profiles of EDW with different angles. (a) 10 cm×10 cm, (b) 20 cm×20 cm |
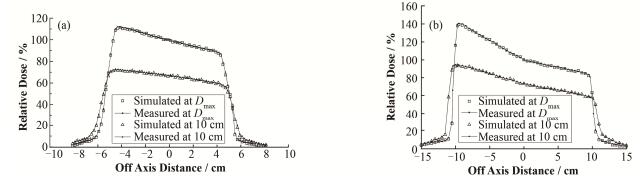
对比10 cm×10 cm、20 cm×20 cm的射野在最大剂量深度(Dmax)和10 cm深度处30° EDW的离轴剂量分布曲线结果如图 5所示,模拟值和测量值取得了很好的一致,偏差小于2%。相对剂量曲线以最大剂量深度射野中心点的剂量归一,蒙特卡罗剂量计算的误差小于1%。其中20 cm×20 cm射野的离轴剂量曲线在-10 -0区间内剂量下降梯度较大,在0-10区间内剂量下降梯度较小。
|
图 5 30° EDW在不同深度的离轴剂量分布曲线 (a) 10 cm×10 cm,(b) 20 cm×20 cm Figure 5 Profiles of EDW with 30° at different depths. (a) 10 cm×10 cm, (b) 20 cm×20 cm |
本研究在BEAMnrc程序中使用DYNJAWS组件模块模拟EDW,生成EDW源模型,使用DOSXYZnrc程序计算体模内剂量,进而计算楔形因子,获得离轴剂量分布。设计几种验证方法,用相同条件的测量结果验证EDW模型,模拟值与测量值取得了较好的一致。由于动态楔形野各点的剂量由STT表决定,而且计算方程也是直接利用挡块位置参数,所以测量均在等中心平面进行,便于保证测量点与计算点一致。对比蒙特卡罗模拟和测量的楔形因子,相同角度的动态楔形板,楔形因子随射野边长的增加平滑减小,且随楔形角的增大这种减小更明显,这主要归因于动态楔形野的形成机制,动态楔形板是利用加速器独立准直器运动和运动过程剂量率的变化来实现楔形剂量分布,对于某一角度楔形野先开野照射一定跳数,然后准直器逐渐关闭形成楔形效果,当射野增大时必然会在楔形野关闭方向形成较高剂量,相应射野中心轴上的累积剂量会降低,从而导致射野中心轴上楔形因子减小。对于小的照射野,蒙特卡罗模拟的楔形因子大于测量的楔形因子,这主要由于电离室测量存在误差,在小野测量时电离室本身的影响就更加明显[13]。相同射野时大楔形角EDW的离轴剂量分布曲线显示蒙特卡罗模拟结果与测量结果偏差较大,尤其在高剂量区蒙特卡罗模拟结果普遍小于测量结果,由于楔形剂量分布是通过准直器不断关闭生成的,在高剂量区照射野变小,二维电离室矩阵对于小照射野的测量同样存在误差。相同楔形角大照射野的EDW离轴剂量分布曲线显示蒙特卡罗模拟结果与测量结果偏差较大,这很可能因为在大照射野生成楔形角时准直器步进幅度变大,Matrixx内部单个电离室的直径是0.45 cm,电离室测量时取体积平均值,不同电离室之间采用了插值,导致测量结果误差变大,而蒙特卡罗模拟过程取单一体素的剂量值,模拟过程体素大小与测量电离室大小不同,分辨率的差异会导致模拟值与测量值产生偏差,并且相应楔形角度的STT表生成精确度对EDW的模拟精度也会产生影响。
EDW在日常计划设计过程中可以用来修正剂量分布,提高放疗的效率,但需要定期执行(Quality Assurance, QA)[14],对比蒙特卡罗模拟和实验测量的楔形因子和离轴剂量分布曲线,二者偏差小于2%,说明本文构建的EDW蒙特卡罗模型是可靠的,为后续EDW放疗计划的蒙特卡罗验证提供了基础,可以作为独立的EDW的QA工具。
| [1] |
Koken P W, Heukelom S, Cuijpers J P, et al. On the practice of the clinical implementation of enhanced dynamic wedges[J]. Medical Dosimetry, 2003, 28(1): 13-19. DOI:10.1016/S0958-3947(02)00140-1 |
| [2] |
Alaei P, Higgins P D. Performance evaluation and quality assurance of Varian enhanced dynamic wedges[J]. Journal of Applied Clinical Medical Physics, 2006, 7(1): 14-20. DOI:10.1120/jacmp.2027.25367 |
| [3] |
于浪, 杨波, 李楠, 等. 应用二维电离室矩阵进行虚拟楔形板物理参数检测[J]. 中华放射肿瘤学杂志, 2015, 24(3): 340-343. YU Lang, YANG Bo, LI Nan, et al. Dosimetry verification of virtual wedge using a two-dimensional ionization chamber array[J]. Chinese Journal of Radiation Oncology, 2015, 24(3): 340-343. DOI:10.3760/cma.j.issn.1004-4221.2015.03.027 |
| [4] |
Varian Oncology Systems. C-series clinac enhanced dynamic wedge implementation guide[R]. Varian, 2002:1-166.
|
| [5] |
Rogers D W O, Faddegon B A, Ding G X, et al. BEAM:a Monte Carlo code to simulate radiotherapy treatment units[J]. Medical Physics, 1995, 22(5): 503-524. DOI:10.1118/1.597552 |
| [6] |
熊绮丽, 石勇, 徐刚, 等. TrueBeam加速器多叶准直器射野剂量学特性[J]. 核技术, 2015, 38(10): 100203. XIONG Qili, SHI Yong, XU Gang, et al. Dosimetry characteristics of multi-leaf collimator field for TrueBeam[J]. Nuclear Techniques, 2015, 38(10): 100203. DOI:10.11889/j.0253-3219.2015.hjs.38.100203 |
| [7] |
Kakakhel M B, Baveas E S, Fielding A L, et al. Validation and automation of the DYNJAWS component module of the BEAMnrc Monte Carlo code[J]. Australasian Physical and Engineering Sciences in Medicine, 2011, 34(1): 83-90. DOI:10.1007/s13246-011-0060-x |
| [8] |
Verhaegen F, Liu H H. Incorporating dynamic collimator motion in Monte Carlo simulations:an application in modelling a dynamic wedge[J]. Physics in Medicine and Biology, 2001, 46(2): 287-296. DOI:10.1088/0031-9155/46/2/302 |
| [9] |
陈亮, 李玉民, 徐红. 瓦里安加速器扩充型动态楔形板楔形因子特性研究[J]. 中华放射肿瘤学杂志, 2004, 13(1): 53-57. CHEN Liang, LI Yumin, XU Hong. Characteristics of wedge factor of an enhanced dynamic wedge on Varian 600C accelerator[J]. Chinese Journal of Radiation Oncology, 2004, 13(1): 53-57. DOI:10.3760/j.issn:1004-4221.2004.01.013 |
| [10] |
Gibbons J P. Calculation of enhanced dynamic wedge factors for symmetric and asymmetric photon fields[J]. Medical Physics, 1998, 25(8): 1411-1418. DOI:10.1118/1.598313 |
| [11] |
Oh S A, Kim S K, Kang M K, et al. Dosimetric verification of enhanced dynamic wedges by a 2D ion chamber array[J]. Journal of the Korean Physical Society, 2013, 63(11): 2215-2219. DOI:10.1118/1.4814791 |
| [12] |
Beavis A W, Weston S J, Whitton V J. Implementation of the Varian EDW into a commercial RTP system[J]. Physics in Medicine and Biology, 1996, 41(9): 1691-1704. DOI:10.1088/0031-9155/41/9/009 |
| [13] |
Ahmad M, Deng J, Lund M W, et al. Clinical implementation of enhanced dynamic wedges into the pinnacle treatment planning system:Monte Carlo validation and patient-specific QA[J]. Physics in Medicine and Biology, 2009, 54(2): 447-465. DOI:10.1088/0031-9155/54/2/018 |
| [14] |
Moeller J H, Leavitt D D, Klein E. The quality assurance of enhanced dynamic wedges[J]. Medical Dosimetry, 1997, 22(3): 241-246. DOI:10.1016/S0958-3947(97)00026-5 |


