研究堆的种类繁多和应用范围广泛，具有运行工况与实验工况复杂、燃料装卸频繁的特点，并且研究堆通常距离居民区较近，因此研究堆的安全特性显得尤为重要。

压力壳型研究堆是研究堆中的一种常见堆型，与池式研究堆不同，压力壳型研究堆的堆芯放置在压力壳中，冷却剂加压强迫循环，冷却效率高于池式堆。这种类型的研究堆功率一般分布在0.2 kW-250 MW，冷却剂运行温度分布在50-300 ℃，运行压力分布在1.1-8.6 MPa^[1]。本文的计算对象高通量工程试验堆(High Flux Engineering Test Reactor, HFETR)属于压力壳型研究堆。

近几年，国内外开展了多项针对研究堆的概率安全分析，比如ATR (Advanced Test Reactor)、Tehran研究堆等。在这些研究堆概率安全分析中，管道破口导致的失水事故是堆芯损坏的重要风险来源。如Greek研究堆概率安全分析中，失水事故与过量反应性引入事故是导致堆芯损坏的支配性始发事件；而在OPAL (Open-pool Australian Lightwater Reactor)研究堆的概率安全分析结果中，地震导致的丧失厂外电和失水事故是堆芯损坏的最大贡献者^[2-3]。因为失水事故在始发事件中非常重要，所以确定失水事故的频率就尤为必要。获得管道破口频率主要有两种途径，分别是：统计已有的运行数据和数值模拟计算。相对于核电厂，研究堆内管道类型繁多，运行工况复杂，目前并没有针对各类型管道的可信统计数据。因此，通过管道破口计算程序获得破口频率就成为可行的方法。

本文以HFETR内反应堆冷却剂出口管道为对象，参考管道破口计算程序PRAISE (Piping Reliability Analysis Including Seismic Events)的方法^[4]，计算了管道焊缝位置发生不同类别破口的频率和累积概率，对其他压力壳型研究堆的管道破口频率计算具有参考价值。

PRAISE计算程序是由美国Science Application公司为劳伦斯利物莫国家实验室(Lawrence Livermore National Laboratory, LLNL)的Load Combination项目开发的计算程序。该程序在核电厂管道破口频率计算中被广泛应用，是一个可靠的管道破口计算程序^[5]。

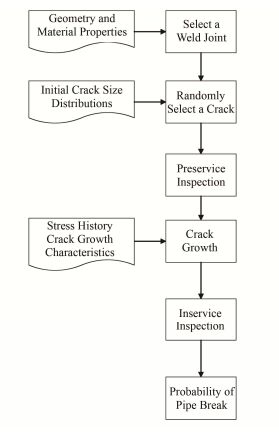
PRAISE程序假定管道焊缝处的破口都是由管道焊缝内壁面上的初始缺陷的增长产生，其计算步骤如下：首先在计算的管道焊缝位置，根据初始缺陷分布抽样得到一个初始内壁缺陷（图 1），然后根据相关工况计算反应堆运行中该缺陷的增长，以及在运行时的常规检查中未发现该缺陷的概率。如果在设计运行年限内缺陷增长导致破口，并且该缺陷未在运行周期开始前的常规检查中被发现，那么判定发生破口事故，并根据破口的相关参数对其进行分类。使用蒙特卡罗方法，通过对初始缺陷的大量抽样，就可以得到该焊缝位置发生各类破口的频率。流程图见图 2。图 2中左侧为程序输入参数，右侧为程序运行步骤。

图 1

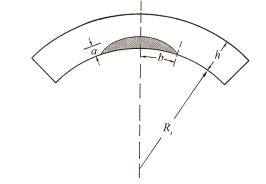
图 1 初始缺陷 Figure 1 Initial crack.

图 2

图 2 总体流程图 Figure 2 Overall flow chart.

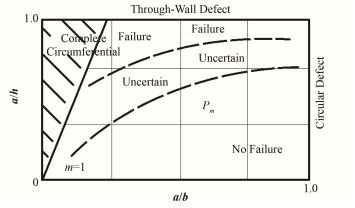
如图 1所示，初始缺陷的尺寸由缺陷深度a、缺陷半宽b和管壁厚度h确定。因此在抽样时，抽取的变量为a/h和a/b。采用这两个参数是因为它们的取值都处于0-1，方便给出初始分布。抽样时为了使样本更均匀和提高抽样效率，可以采用分层抽样。抽样示意图见图 3，图 3中矩形的横向为a/b的取值，纵向为a/h的取值，矩形中的点表示抽样中可能出现的所有值。左侧的阴影区域内的点表示完全环绕管道内壁的初始缺陷，此类缺陷在计算中不予考虑。矩形上部的点比下部的点更容易导致破口发生。在分层抽样中，将计算区域划分为m层，对应为图 3中的方格，P_m为每个方格自身的概率。

图 3

图 3 抽样示意图 Figure 3 Sampling schematic.

在计算缺陷增长时，首先分别计算出一个运行周期中缺陷深度a和半宽b的均方应力强度因子的最大值${\overline K _{\max }}$和最小值${\overline K _{\min }}$，之后根据式(1)得到a和b的有效均方应力强度因子${(\Delta \overline K )_{{\rm{eff}}}}$，再将其与临界应力强度因子K_o作比较，只有当${(\Delta \overline K )_{{\rm{eff}}}}$大于临界应力强度因子时，缺陷增长，增长幅度为$C{(\Delta \overline K )_{{\rm{eff}}}}^4$。其中：C为疲劳裂纹增长参数。

在破口发生后，根据运行中是否进行超声波检查，在程序中可分为两种情况：

第一种情况是不进行超声波检查，那么所有的破口均不会在发生前被检测到，计算后，在时间t之前发生破口的概率由式(2)给出，其中：N_{F, m}(t)表示第m层抽样中在时间t之前发生破口的样本数目；N_m表示第m层抽样总数；p_m表示m层抽样本身的概率。

第二种情况是在每一个运行周期开始前，对管道进行超声波检查。在程序中，缺陷未在超声波检查中被发现的概率由式(3)-(5)给出。其中：D_B为超声波束的直径，取2.54 cm；υ取1.60；a^*取管道壁厚的一半。

由于不同的核电厂对管道运行的检查并不相同，PRAISE程序中给出的只是破口检测概率的一个简单计算方法。对于一个确定的计算对象，破口检测概率的计算应当根据具体的检测情况得出。

计算后，在时间t之前发生破口的概率由式(6)给出，其中：P_{ND, m}(t)表示m层抽样中在时间t之前发生的破口未被检测到的概率，将其求和来替代N_{F, m}(t)。

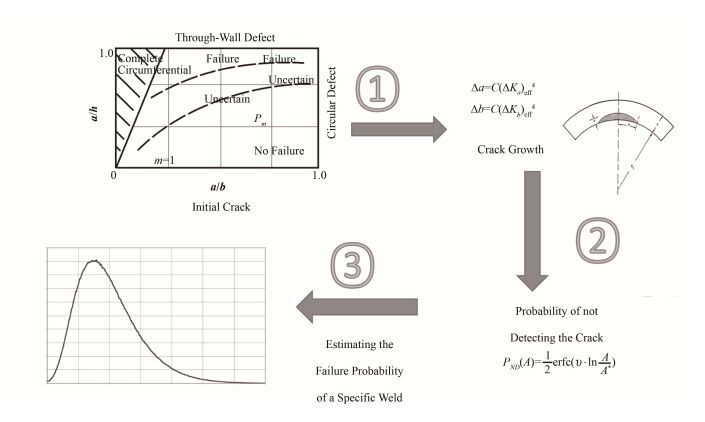
PARISE程序的主要计算方法见图 4。

图 4

图 4 PRAISE程序示意图 Figure 4 Schematic of PRAISE program.

HFETR是我国自主设计建造的压力壳型研究堆，反应堆热功率为125 MW，出口温度71.0 ℃，出口压力1.1 MPa，每月开堆^[6]。

本文选取了HFETR的反应堆冷却剂出口管道处的焊缝作为计算对象^[7-8]，管道内径为696 mm，壁厚为12.5 mm，运行压力为1.1 MPa，运行温度为71 ℃，管道材料密度为8 g∙cm^-3。计算运行10 a。其中管道壁厚参考了国家标准GB/T 17395-2008^[9]。

使用PRAISE程序计算一个特定焊缝发生破口的概率时，需要考虑此焊缝内包含的初始缺陷数目。而焊缝中缺陷与管道材料、焊接方式以及管道的运行参数密切相关^[10]，不同材料之间的初始缺陷数目会有很显著的差别^[11]。由于目前无法确切的获取高通量工程试验堆冷却剂出口管道的材料及焊接方式，参考已有的管道破口分析^[12]，对于仅考虑初始缺陷的蒙特卡罗模拟，可以只计算一个初始缺陷。因此本文只计算高通量堆出口管道焊缝处的一个初始缺陷。

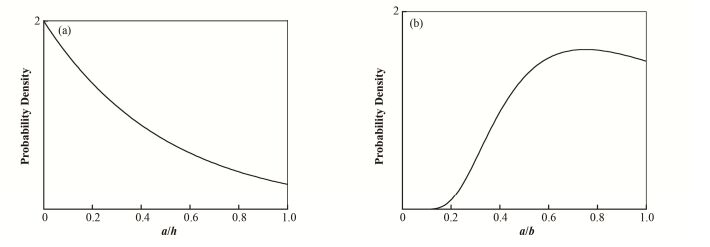
经过计算，当采用30×30的分层，每一层抽取200个样本，样本总数共计180000时，计算结果趋于稳定。计算中a/h和a/b参数的分布分别按照式(7)、(8)采用指数型分布，其概率密度函数见图 5。

图 5

图 5 a/h (a)和a/b (b)的概率密度分布 Figure 5 Probability density distribution of a/h (a) and a/b (b).

对于初始缺陷的分布形式，本文采用了PRAISE程序中给出的指数型分布表达式。

式中：μ₁和μ₂的取值参考了程序计算样例中的取值^[4]。

当破口发生后，根据破口导致的事故后果将其分为4类。

当量直径小于20 mm的破口作为第一类。此类破口由于尺寸很小，所以发生后并不会导致停堆。

当量直径大于20 mm且破口截面积小于Dδ/4的破口作为第二类。其中：D为管道外径；δ为管道壁厚。此类破口尺寸大于第一类，发生之后会导致停堆，需要操作人员及时采取缓解措施。

截面积大于Dδ/4的破口作为第三类。此类破口发生后，将会导致反应堆堆芯损坏。

导致管道双端断裂的破口作为第四类。此时发生大破口失水事故，严重影响反应堆安全。

计算中根据是否对管道进行超声波检查分为两种情况。因为对高通量堆的管道运行检查情况并不清楚，此处直接采用PRAISE程序中给出的破口检测概率计算方法。

当反应堆运行中不进行超声波检查时，计算得到运行10 a间各类破口发生频率和10 a累积概率如表 1所示。其中10 a累积概率表示运行10 a的破口频率之和，是10 a里破口发生的总概率。

表 1

表 1 高通量堆破口频率计算结果（不检查） Table 1 Results of the break frequency calculation of HFETR (without examination). 年份Year 第一类破口Type 1 第二类破口Type 2 第三类破口Type 3 第四类破口Type 4 1 5.83×10-4 1.946×10-5 2.250×10-7 4.257×10-23 2 2.97×10-4 5.420×10-6 1.386×10-7 6.081×10-24 3 1.47×10-4 6.890×10-6 3.270×10-8 1.824×10-23 4 1.62×10-4 4.150×10-6 7.589×10-8 1.824×10-23 5 1.37×10-4 9.771×10-7 7.330×10-8 6.081×10-24 6 1.02×10-4 2.605×10-6 5.021×10-8 1.258×10-23 7 1.10×10-4 2.219×10-6 2.720×10-8 3.250×10-23 8 8.77×10-5 1.308×10-6 1.645×10-8 1.300×10-23 9 6.22×10-5 2.171×10-6 8.159×10-9 6.500×10-24 10 7.33×10-5 2.480×10-6 4.206×10-8 0 10 a累积Summation of 10 a 1.76×10-3 4.770×10-5 6.900×10-7 1.560×10-22

表 1 高通量堆破口频率计算结果（不检查） Table 1 Results of the break frequency calculation of HFETR (without examination).

计算结果显示，第一类破口发生的频率最高，位于10^-5-10^-4量级，10 a累积概率为1.76×10^-3，此类破口较小，对反应堆安全的影响不大；第二类破口发生的频率位于10^-7-10^-5量级，10 a累积概率为4.77×10^-5，此类破口可通过及时采取措施得到缓解；第三类破口发生的频率位于10^-9-10^-7量级，10a累积概率为6.90×10^-7。此类破口会导致反应堆堆芯损坏，需要给予重视；第四类破口发生的频率位于10^-24-10^-23量级，10 a累积概率为1.56×10^-22，频率远低于前三类。

从表 1中可以看出，4类破口的频率均于第一年达到最大值，之后有明显下降，并随着运行年限的增加而趋于稳定。

当反应堆在开堆前对管道进行超声波检查时，计算得到的运行10 a间各类破口发生频率和10 a累积概率如表 2所示。

表 2

表 2 高通量堆破口频率计算结果（检查） Table 2 Results of the break frequency calculation of HFETR (with examination). 年份Year 第一类破口Type 1 第二类破口Type 2 第三类破口Type 3 第四类破口Type 4 1 4.295×10-5 8.688×10-7 1.339×10-8 2.8782×10-24 2 1.731×10-5 2.945×10-7 3.191×10-9 3.5510×10-25 3 1.117×10-5 1.904×10-7 2.832×10-9 1.0846×10-24 4 8.110×10-6 1.400×10-7 3.274×10-9 1.0827×10-24 5 6.443×10-6 2.635×10-7 4.738×10-9 3.6463×10-25 6 6.420×10-6 1.343×10-7 1.752×10-9 7.4377×10-25 7 5.839×10-6 1.950×10-7 6.705×10-10 1.5465×10-24 8 4.228×10-6 1.490×10-7 1.286×10-9 3.8354×10-25 9 5.338×10-6 1.696×10-7 4.133×10-9 3.8355×10-25 10 5.060×10-6 6.921×10-8 3.316×10-10 0 10 a累积Summation of 10 a 1.130×10-4 2.470×10-6 3.560×10-8 8.8200×10-24

表 2 高通量堆破口频率计算结果（检查） Table 2 Results of the break frequency calculation of HFETR (with examination).

计算结果显示，进行超声波检查之后，各类破口频率均下降了一个数量级。第一类破口发生的频率位于10^-6-10^-5量级，10 a累积概率为1.13×10^-4；第二类破口发生的频率位于10^-8-10^-7量级，10 a累积概率为2.47×10^-6；第三类破口发生的频率位于10^-10-10^-8量级，10 a累积概率为3.56×10^-8；第四类破口发生的频率位于10^-25-10^-24量级，10 a累积概率为8.82×10^-24。

从表 2中可以看出，与进行超声波检查时一样，4类破口的频率均于第一年达到最大值，之后明显下降，并随着运行年限的增加而趋于稳定。

在破口频率的计算中，不确定性来自于两个方面：一个是物理量本身存在不确定性，比如管道的温度和压力在运行中会存在一定的波动；另一个是计算模型中存在的不确定性，比如样本空间有限，以及建立的模型与物理实际之间的偏差。本文已确定了计算模型，所以只考虑物理量本身的不确定性。

对于蒙特卡罗方法，敏感性分析可以给出输入参数的变化对计算结果的影响，在此基础上，不确定性分析中需要重点分析敏感性高的运行参数。因为在管道实际运行中，敏感性高的运行参数的波动可能会对破口频率产生较明显的影响。

根据敏感性分析，在不涉及地震的计算中，初始缺陷尺寸和热应力是PRAISE程序中对结果产生重要影响的关键参数^[11]。具体到输入参数上，就是温度、压力以及确定初始缺陷分布的参数（式(7)和(8)中的μ₁和μ₂）。

在计算中将温度、压力和初始缺陷分布参数设置为具有特定分布的随机变量，此时可对计算结果进行不确定性分析，得到分位值。当所有输入参数都为确定值时，计算得到的结果为最佳估计值。

不确定性分析中，温度、压力以及初始缺陷分布参数见表 3。

表 3

表 3 输入参数分布 Table 3 Probability distributions of input parameters. 名称Name 分布类型Type 期望Expected value 分位值Percentile 5th 95th 温度Temperature 正态分布Normal distribution 71 ℃ 66 ℃ 76 ℃ 压力Pressure 对数正态分布Log-normal distribution 1.1 MPa 0.8 MPa 1.43 MPa μ1 对数正态分布Log-normal distribution 4 2.57 5.84 μ2 对数正态分布Log-normal distribution 1.5 0.96 2.18

表 3 输入参数分布 Table 3 Probability distributions of input parameters.

经过计算，可以得到4类破口10 a累积概率的分位值及最佳估计值（表 4和表 5）。

表 4

表 4 计算结果不确定性分析（不检查） Table 4 Uncertainty analysis of computation result (without examination). 分位值Percentile 最佳估计 Best estimate 5% 50% 95% 第一类破口Type 1 8.30×10-4 1.74×10-3 2.47×10-3 1.76×10-3 第二类破口Type 2 4.16×10-6 5.10×10-5 2.24×10-4 4.77×10-5 第三类破口Type 3 7.75×10-9 1.01×10-6 2.02×10-5 6.90×10-7 第四类破口Type 4 7.80×10-32 2.30×10-21 8.15×10-16 1.56×10-22

表 4 计算结果不确定性分析（不检查） Table 4 Uncertainty analysis of computation result (without examination).

表 5

表 5 计算结果不确定性分析（检查） Table 5 Uncertainty analysis of computation result (with examination). 分位值Percentile 最佳估计 Best estimate 5% 50% 95% 第一类破口Type 1 6.32×10-5 1.13×10-4 1.65×10-4 1.13×10-4 第二类破口Type 2 4.16×10-7 2.90×10-6 1.20×10-5 2.47×10-6 第三类破口Type 3 1.12×10-9 5.21×10-8 9.59×10-7 3.56×10-8 第四类破口Type 4 2.51×10-31 2.05×10-23 8.58×10-17 8.82×10-24

表 5 计算结果不确定性分析（检查） Table 5 Uncertainty analysis of computation result (with examination).

本文参考管道破口计算程序PRAISE的方法，根据高通量工程试验堆的运行工况，对其反应堆冷却剂出口管道的一个焊缝进行了计算，得到了运行10 a间该处焊缝发生各类破口的频率和10 a累积概率，并对计算结果进行了分析。

本文首先得到了各类破口发生的频率。计算中将破口分为4类：第一类和第二类破口发生频率较高，分别为10^-5-10^-4量级和10^-7-10^-5量级，这两类破口虽然频率高，前者破口截面积较小，不会导致停堆，后者通过操作人员及时采取措施可以得到缓解；第三类破口发生的频率为10^-9-10^-7量级，此类破口会导致反应堆堆芯损坏，需要重点关注；第四类破口是管道双端断裂，此类破口发生的频率极低，为10^-24-10^-23量级。

通过计算还得出，开堆前进行超声波检查，各类破口频率均下降了一个数量级，这表明运行前检查可以有效降低管道破口发生的频率。