2. 中国科学院大学 北京 100049;
3. 中国科学院钍基熔盐核能系统研究中心 上海 201800
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Center for Thorium Molten Salt Reactor System, Chinese Academy of Sciences, Shanghai 201800, China
针对熔盐堆中的传热和流动过程,计算流体力学(Computational Fluid Dynamics, CFD)软件使用数值方法进行状态方程求解有大量的计算需求。传统的中央处理器(Central Processing Unit, CPU)并行计算已经不能很好的满足计算性能的要求,而通用图形处理器(General-purpose Graphic Processing Units, GPGPUs)的快速发展使得许多开发程序由CPU并行计算转向GPU并行计算。
目前国内外已有使用GPU开发程序的相关研究。应智等[1]进行了基于GPU的OpenFOAM并行加速研究。在OpenFOAM上使用GPU解算器插件求解不同规模的经典CFD圆柱扰流,能够得到超过6倍的加速比并验证了GPU加速方法的正确性。Wienke等[2]通过两个实际应用的例子,对比了OpenCL和OpenACC两种GPU加速方法的效率。OpenACC的加速效果只能分别达到OpenCL的0.8和0.4倍。然而,OpenCL修改了630条代码,OpenACC只修改了46条代码。Wyrzykowski等[3]通过OpenACC编程技术,实现了稳定双共轭梯度算法的GPU并行化。该算法用在CPU与两种GPU上,GPU并行化后的程序分别可以加速2.38和6.25倍。Kraus等[4]在德国的CFD流体求解器ZFS上使用OpenACC编程技术实现了GPU并行加速,仅加入71条代码就能达到两倍以上的加速比。
本文利用GPU并行加速技术对Code_Saturne进行二次开发并应用于熔盐堆堆芯流场分析。通过分析Code_Saturne的计算流程,在Code_Saturne的求解器模块求解压力状态方程中实现了预处理共轭梯度算法的GPU并行化及性能优化。
1 GPU计算平台美国Sandia国家实验室的一项模拟测试显示,在传统架构下,由于存储机制和内存带宽的限制,16核CPU以上处理器不仅不能为超级计算机带来性能提升,甚至可能导致效率大幅度下降[5]。自从NVIDIA公司发布了基于G80的并行编程模型和C语言开发环境CUDA (Compute Unified Device Architecture),GPGPUs快速的发展起来。GPU并行开发主要有两种语言:一种是以CUDA为首的基于硬件结构的编程语言等;另一种是以OpenACC为首的基于指导语句的编程语言。指导语句的编程语言是指为现有的编程语言添加对GPU的支持,用户只要在需要GPU并行的区域添加编译标记,再由相应的编译器处理就可以在GPU平台上运行。本文使用的GPU并行技术是OpenACC,目前仅支持C/C++和Fortran两种语言,语法规则与OpenMP相似。
2 基于OpenACC的Code_Saturne程序加速 2.1 熔盐堆堆芯热工水力计算熔盐堆是第四代堆型中唯一使用液态燃料的反应堆,且液态燃料多为高温熔融的氟化盐。为了降低熔盐堆堆芯模型几何结构的复杂度及减少计算时间,本文在进行数值模拟计算分析时,对几何模型进行简化处理。计算模型包含下降环腔、熔盐进出口管道和堆芯熔盐通道三个部分的熔盐堆堆芯模型,熔盐从进口管道流入,经过下降段进入堆芯,最后从堆芯流出。选取开源CFD软件Code_Saturne对熔盐堆堆芯流场进行简单模拟计算。
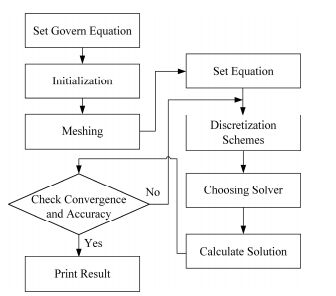
计算流体动力学是通过数值计算对流体流动和热传导等相关物理现象的系统进行分析。其基本思想类似于微积分,是将用一系列有限的变量值代替连续的物理量[6]。流体流动都要遵守物理守恒定律,想要对其进行描述,就必须通过数学的方程来进行,其中控制方程(Governing Equations)是这些守恒定律的数学描述。如图 1所示,从CFD工作流程图可以看出,采用CFD方法对流体的流动问题进行数值模拟的基础就是建立控制方程。通过基本守恒定律的分析,可以导出流体的连续性方程、动量方程及能量方程,写成式(1)的通用形式[7]。
|
图 1 CFD工作流程 Figure 1 Overview of CFD. |
| $\frac{{\partial \left( {\rho \phi } \right)}}{{\partial t}} + \nabla \cdot \left( {\rho u\phi } \right) = \nabla \cdot \left( {\mathit{\Gamma }\nabla \phi } \right) + S$ | (1) |
式中:φ为通用变量,可以代表u、v、w、T等求解变量;ρ是密度;u是速度矢量;t是时间;Γ为广义扩散系数;S为广义源项。
通过数值解法,可以将连续的偏微分方程离散为有限未知量的代数方程组。本文的Code_Saturne程序利用有限体积法进行离散。以二维瞬态对流-扩散问题为例,控制方程(1)可以写成[6]:
| $\begin{array}{l} \frac{{\partial \left( {\rho \phi } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho u\phi } \right)}}{{\partial x}} + \frac{{\partial \left( {\rho v\phi } \right)}}{{\partial y}}\\ \quad = \frac{\partial }{{\partial x}}(\mathit{\Gamma } \cdot \frac{{\partial \phi }}{{\partial x}}) + \frac{\partial }{{\partial y}}(\mathit{\Gamma } \cdot \frac{{\partial \phi }}{{\partial y}}) + S \end{array}$ | (2) |
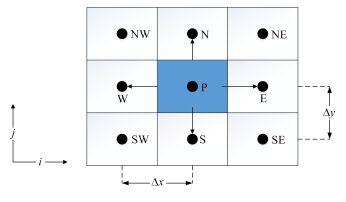
假设P为一个广义的计算节点,记其左右两侧的相邻节点分别为E和W,上下两侧用的相邻节点分别为S和N,如图 2所示。
|
图 2 有限体积法体控制方程离散示意图 Figure 2 Governing equations discretization of finite element method. |
对图 3所示的P点处的控制体在∆t的时间段内进行积分可得:
| $\begin{array}{l} \int_t^{t + \Delta t} {\int_{\Delta V} {\frac{{\partial \left( {\rho \phi } \right)}}{{\partial t}}} } {\rm{d}}V{\rm{d}}t + \int_t^{t + \Delta t} {\int_{\Delta V} {\left( {\frac{{\partial \left( {\rho u\phi } \right)}}{{\partial x}} + \frac{{\partial \left( {\rho v\phi } \right)}}{{\partial y}}} \right)} } {\rm{d}}V{\rm{d}}t\\ = \int_t^{t + \Delta t} {\int_{\Delta V} {\left( {\frac{\partial }{{\partial x}}(\mathit{\Gamma } \cdot \frac{{\partial \phi }}{{\partial x}}) + \frac{\partial }{{\partial y}}(\mathit{\Gamma } \cdot \frac{{\partial \phi }}{{\partial y}})} \right)} } {\rm{d}}V{\rm{d}}t + \int_t^{t + \Delta t} {\int_{\Delta V} S } {\rm{d}}V{\rm{d}}t \end{array}$ | (3) |
如果在对流项、扩散项和源项中引入全隐式的时间积分方案,二维瞬态通用形式的代数方程可写为:
| ${a_p}{\phi _p} = \sum {{a_{nb}}{\phi _{nb}}} + b$ | (4) |
式中:φp是控制体积p上的待求物理量,可以是三个方向速度u、v、w和压力p,还可以是温度T等;b为源项,下标nb表示相邻节点。
从通用形式的代数方程可以看出,压力项没有自身的控制方程,压力的修正值和正确的速度场如何得到成为迭代过程中的难题。所以Patankar和Spalding在1972年提出了求解压力耦合方程组的半隐式方法[7]。本文采用的Code_Saturne程序利用半隐式方法算法进行离散方程组的求解,其中需要大量的迭代计算。一般的CFD软件采用较多的迭代法有共轭梯度法和代数多重网格法。由于预处理技术常用来加速矩阵求解收敛速度的方法,所以本文的Code_Saturne程序为了加快收敛速度,使用了预处理技术的共轭梯度法作为迭代算法。
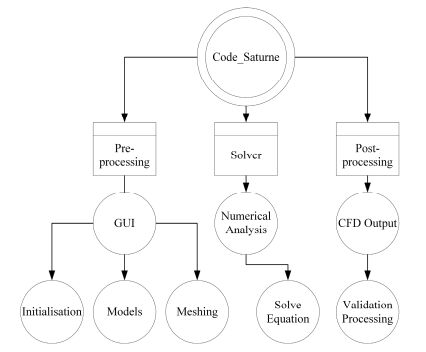
2.2 开源CFD软件Code_Saturne的介绍Code_Saturne是由法国EDF (Electricity of France)集团研发中心研发的一款通用计算流体力学软件。Code_Saturne是基于有限体积法,适用于处理二维、三维,稳态或非稳态,层流或湍流等多种计算问题[8]。Code_Saturne有前处理器、求解器、后处理器三大模块,并通过可视化用户界面将三大模块整合起来。如图 3所示,Code_Saturne程序的求解器模块将物理问题转化为求解代数方程组,采用迭代求解的算法进行方程组的求解。本文以4.0.6版本的Code_Saturne程序为基础,使用PGI编译器进行编译。
|
图 3 Code_Saturne结构概览 Figure 3 Overview of Code_Saturne structure. |
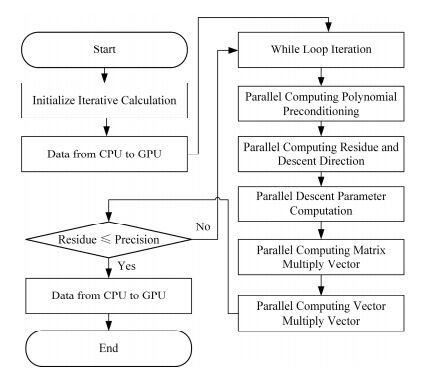
因为迭代求解在Code_Saturne软件模拟计算中占了80%的计算时间[9],所以利用OpenACC编程技术对其耗时最长的部分进行GPU并行加速。在软件自带的预处理共轭梯度算法求解压力状态方程中,该求解算法的while循环部分占了大部分运算时间,而其中耗时最长的是矩阵向量相乘。所以本文将OpenACC编程技术应用于Code_Saturne中压力状态方程求解的预处理共轭梯度算法。通过OpenACC语法中的两个计算构件将循环并行化,分别为parallel和kernels。这两个构件通过使用子语指定下方的循环区域需要GPU并行和并行级别。如图 4所示,GPU并行化处理之前,还需要将所需变量存储于GPU上,可以减少CPU与GPU之间的重复数据拷贝时间。在并行计算结束时,运算所得数据也需要从CPU端拷贝到GPU端。
|
图 4 GPU上CG迭代并行处理流程图 Figure 4 Parallel processing flow chart of CG on GPU. |
主流加速器的编程语言及兼容性问题使GPU加速原有程序比较困难,而OpenACC是一种指导语句,只与编译器的种类相关。本文采用条件编译方法将GPU并行算法嵌入源代码,可以根据其需求进行编译及修改,使得程序本身拥有更好的兼容性。使用OpenACC编程的条件编译方法需要相应的编译器预定义一个宏_OPENACC,其中宏的值由OpenACC版本的发布日期构成。
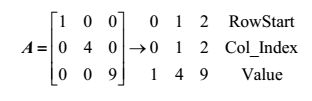
2.4.2 数据存储稀疏矩阵的存储格式在向量矩阵相乘中是影响运算性能的关键因素[10-11]。在GPU平台上能够有较好的运算性能的格式有行压缩(Compressed Sparse Row, CSR)、ELLPACK (ELL)和分片ELL (Sliced ELLPACK, SELL)。本文采用了两种适合GPU并行格式,一种是CSR,如图 5所示。RowStart存储了每行第一个非零元在Value中的索引,Col_Index存储了非零元的列索引,Values存储了所有非零元的具体值。另一种是CSR的变种MSR (Modified CSR),用于分块存储数据。本文通过使用基于Fortran语言的接口函数进行矩阵格式的修改,在求解压力状态方程之前显示地将矩阵存储格式转换为CSR格式。
|
图 5 CSR存储格式 Figure 5 CSR storage format. |
迭代计算会被大量的线程并行执行,将数据空间进行划分,映射到GPU线程上。给出每个线程块中最优配置值,从而在GPU上得到更好的并行效率。当一个线程块中的线程数较大时,GPU可以通过在不同的快速切换来隐藏访存延迟,因此增大一个线程块中的线程数有助于提高计算资源的利用率[1]。本文使用OpenACC实现GPU并行加速,而OpenACC拥有三个并行层次,分别为gang、worker和vector。每个层次的并行个数可以通过相应的子语来实现。本文使用NVIDIA公司生产的Tesla K40c,每个流处理器的最多可以同时处理1024个线程。当gang、worker和vector的数分别在1、32和32时,预处理共轭梯度法的GPU并行计算达到最优性能。
3 测试方案 3.1 测试环境本文搭建了如下测试环境来验证GPU加速并行方法的正确性及其加速性能。本文在Linux系统中安装了开源CFD软件Code_Saturne及其相关组件,Code_Saturne是4.06版本,PGI编译器为4.4.3版本。以个人工作站作为实验平台,其中的GPU为NVIDIA公司生产的Tesla K40c,CPU为6核Intel Xeon E5-2620。
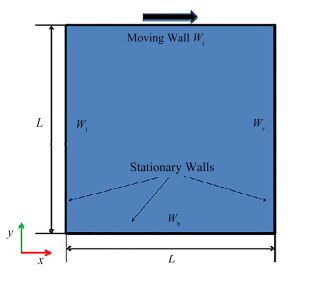
3.2 测试结果 3.2.1 正确性验证方腔顶盖驱动流是经典的数值计算模型,常用来检测源程序和计算思想的正确性。本文模拟的方腔边长L为1m,速度v=1m·s−1,即其顶板以1m·s−1速度向右移动,同时带动方腔内流体的流动,流场内的流体为层流,如图 6所示。空腔中充满等密度的水,密度为1.0kg·m−3,动力粘度为10−3Pa·s−1,那么雷诺数为1000。计算区域示意图[12]如图 6所示。
|
图 6 顶盖驱动流示意图 Figure 6 Lid-driven cavity flow. |
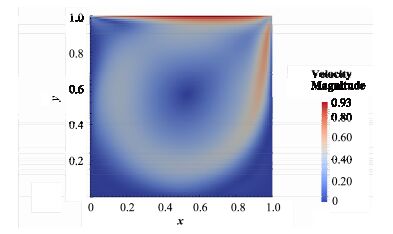
为了验证GPU并行算法的正确性,本文测试了方腔驱动流的流场计算结果,并与GPU加速前的结果进行了比较。图 7为使用GPU加速后的流场计算结果,GPU加速前后的结果相差很小。
|
图 7 方腔驱动流的流场算例GPU加速后 Figure 7 Velocity field of lid-driven cavity flow case after GPU parallelization. |
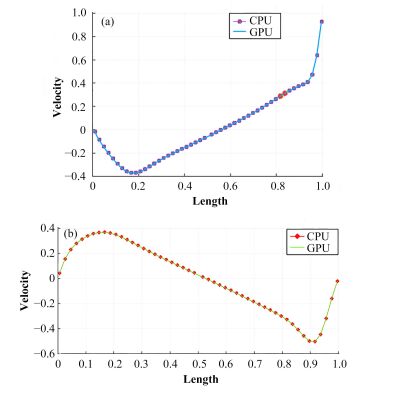
图 8(a)为GPU与CPU的沿着y轴中心截面x方向的流速结果,图 8(b)为GPU与CPU的沿着x轴中心截面y方向的流速结果。从测试结果来看,无论是沿着y轴中心截面x方向,还是沿着x轴中心截面y方向,GPU得出的结果与CPU的结果相差很小,证明了该方法的正确性。
|
图 8 沿y轴中心截面x方向(a)和沿x轴中心截面y方向(b)的流速分布 Figure 8 x velocity along the y-axis (a) and y velocity along the x-axis (b). |
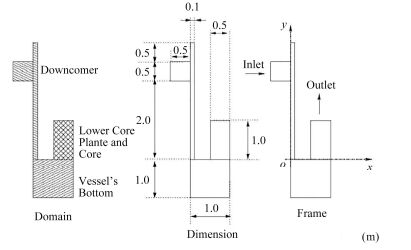
本文采用了简化的熔盐堆堆芯模型模拟堆芯流场的计算。入口位于下降段的左边,熔盐FLiBe以速度为1m·s−1、温度为600℃进入堆芯。熔盐的密度为1986.55354kg·m−3,动力粘度为8.554× 10−3Pa·s−1,导热系数为1.1W·m−1·K−1,定压比热容为2390J·kg−1·℃−1,湍流模型为k-ε模型。出口位于堆芯的上方,堆芯的几何参数[13]如图 9所示。
|
图 9 简易熔盐堆模型示意图 Figure 9 Simplified molten salt reactor. |
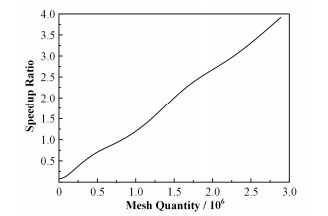
通过GPU加速技术将向量内积算法部分进行并行加速,统计加速前后所用时间及计算对应的加速比。由于向量运算只涉及一维运算,存储和计算都有利于并行运算。从图 10中可以看出,当网格规模达到2.89×106时,计算速度是原有程序的3.92倍,加速效果明显。从整体上看,随着网格规模的增大,向量内积算法加速比呈线性上升趋势。
|
图 10 向量内积运算加速比曲线 Figure 10 Dot product speedup curve. |
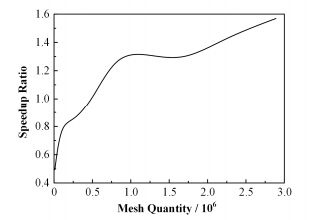
通过GPU加速技术将矩阵向量相乘算法部分进行并行加速,并统计加速前后所用时间及计算对应的加速比。将矩阵存储为方便GPU并行计算的CSR格式,向量的存储格式不改变。如图 11所示,在网格规模相同的情况下,矩阵向量相乘算法部分优化效果并不理想,只是CPU串行计算速度的1.56倍,通过进一步的测试,赋予数据空间和数据传输消耗了大量的计算时间。但是从整体上看,随着网格规模的增大,矩阵向量算法加速比大致呈线性上升趋势。
|
图 11 矩阵向量乘法 Figure 11 Sparse matrix vector multiply speedup curve. |
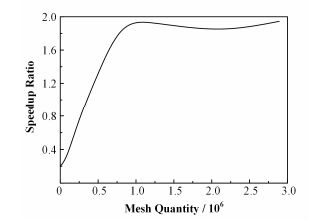
图 12为不同网格规模下预处理共轭梯度法的加速比率。从图 12中可以看出,在网格规模数为8.1×105时,GPU优化后的计算性能达到顶峰,加速比为1.93;而在网格规模数大于8.1×105时,GPU优化后的加速性能基本上维持不变。将其中的向量及矩阵线性运算GPU并行化,把需要计算的数据从CPU端拷贝到GPU端,可以减少数据的拷贝时间。需要注意的是,拷贝的数据量要适当,过多可能造成带宽拥堵,过少可能造成数据的读取效率低下。Code_Saturne使用预处理共轭梯度法进行状态方程求解时,临时矩阵和向量的变量很多。当GPU中存储的数据较多时,由于带宽的限制和GPU内数据的读取等问题,加速效果不明显。
|
图 12 预处理共轭梯度法 Figure 12 Preconditioned conjugate gradients speedup curve. |
本文将开源CFD软件Code_Saturne中稀疏线性迭代求解的过程实现了GPU并行化,对数据存储和分配进行了优化。通过对开源CFD软件中稀疏线性求解算法的研究,建立了基于OpenACC的GPU并行算法。通过与原版程序计算结果进行对比,验证了GPU并行算法的正确性。OpenACC能够用比较小的代价实现大量代码的加速,仅在源代码中加入不超过40条OpenACC代码。通过GPU并行化后的Code_Saturne程序对熔盐堆堆芯流场简单模拟测试可以看出,随着网格数量的增加,预处理共轭梯度法的加速比逐渐增大,特别是向量线性运算加速明显,说明该算法具有良好加速性能。
| [1] |
应智. 基于GPU的OpenFOAM并行加速研究[D]. 上海: 上海交通大学, 2012. YING Zhi. Research on acceleration of open FOAM based on GPU[D]. Shanghai:Shanghai Jiaotong University, 2012 http://cdmd.cnki.com.cn/Article/CDMD-10248-1012018545.htm |
| [2] |
Wienke S, Springer P, Terboven C, et al. OpenACC:first experiences with real-world applications[C]. Berlin:Euro-Par 2012 Parallel Processing, 2012:859-870
|
| [3] |
Wyrzykowski R, Dongarra J, Karczewski K, et al. Parallel processing and applied mathematics[M]. Berlin: Springer Berlin Heidelberg, 2008, 311-321.
|
| [4] |
Kraus J, Schlottke M, Adinetz A, et al. Accelerating a C++ CFD code with OpenACC[C]. 2014 First Workshop on Accelerator Programming Using Directives (WACCPD), Los Alamitos, USA, 2014:47-54
|
| [5] |
张朝晖, 刘俊起, 徐勤建. GPU并行计算技术分析与应用[J]. 信息技术, 2009, 11: 86-89. ZHANG Zhaohui, LIU Junqi, XU Qinjian. Analysis and application of the GPU parallel computing technology[J]. Information Technology, 2009, 11: 86-89. DOI:10.3969/j.issn.1674-2117.2009.04.050 |
| [6] |
王福军. 计算流体动力学分析:CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004, 54-57. WANG Fujun. Computational fluid dynamic analysis:theory and application of CFD[M]. Beijing: Tsinghua University Press, 2004, 54-57. |
| [7] |
宋士雄. 熔盐冷却球床堆热工水力特性研究[D]. 上海: 中国科学院上海应用物理研究所, 2014. SONG Shixiong. Thermal-hydraulics characteristics research of molten salt cooled pebble bed reactor[D]. Shanghai:Shanghai Institute of Applied Physics, Chinese Academy of Sciences, 2014 http://cdmd.cnki.com.cn/Article/CDMD-80014-1015033051.htm |
| [8] |
Anzt H, Baboulin M, Dongarra J, et al. Accelerating the conjugate gradient algorithm with GPUs in CFD simulations[C]. High Performance Computing for Computational Science, VECPAR, Porto, Portugal, 2016:35-43
|
| [9] |
Rodriguez M R, Philip B, Wang Z, et al. Block-relaxation methods for 3D constant-coefficient stencils on GPUs and multicore CPUs[EB/OL]. 2017-01-05. https://arxiv.org/pdf/1208.1975v2.pdf
|
| [10] |
张志能. 基于GPU的稀疏线性方程组求解及其应用[D]. 南昌: 南昌大学, 2013. ZHANG Zhineng. Solution and application of sparse linear system based on GPU[D]. Nanchang:Nanchang University, 2013 http://cdmd.cnki.com.cn/Article/CDMD-10403-1013344055.htm |
| [11] |
马超, 韦刚, 裴颂文, 等. GPU上稀疏矩阵与矢量乘积运算的一种改进[J]. 计算机系统应用, 2010, 19(5): 116-120. MA Chao, WEI Gang, PEI Songwen, et al. Improvement of sparse matrix-vector multiplication on GPU[J]. Computer Systems & Applications, 2010, 19(5): 116-120. |
| [12] |
Shear driven cavity flow[EB/OL]. 2012-10-27. http://code-saturne.org/cms/sites/default/files/file_attach/Tutorial/version-3.0/Shear-driven-cavity-flow.pdf
|
| [13] |
Simplified nuclear vessel[EB/OL]. 2013-01-05. http://code-saturne.org/cms/sites/default/files/file_attach/Tutorial/version-3.0/Simplified-nuclear-vessel.pdf.
|


