2. 中国科学院大学 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
熔盐堆(Molten Salt Reactor, MSR)是第四代国际核能论坛(Generation IV International Forum, GIF)推荐的6种先进四代堆候选堆型之一[1],采用流动的熔盐作为燃料和冷却剂,具有资源的可持续性、高度的安全性、良好的经济性和可靠的防扩散性等特点,满足核能可持续发展的需要[2]。熔盐堆与传统固体燃料反应堆不同,熔盐的流动性使熔盐堆有其独有特性:流动的熔盐既是燃料又是冷却剂与慢化剂;裂变热主要释放在熔盐中;缓发中子先驱核(Delayed Neutron Precursor, DNP)随熔盐流出堆芯造成堆芯反应性降低。
熔盐实验堆(Molten Salt Reactor Experiment, MSRE)是美国橡树岭国家实验室(Oak Ridge National Laboratory, ORNL)于20世纪40年代提出并建造的熔盐试验堆[3],它从1965年运行到1969年,运行功率为8 MW。堆芯主要由流动的熔盐燃料与石墨慢化剂通道组成,其中熔盐的主要成分是裂变材料235U或233U的氟化物与锂铍(Li、Be)的氟化物[3]。
由于熔盐堆的堆芯物理参数有其特殊之处,为了验证熔盐堆的可行性,许多研究机构提出了各种不同的概念设计方案。如法国电力公司提出AMSTER (Actinides Molten Salt TransmutER)设计[4];日本提出了FUJI MSR设计[5];2011年中国科学院上海应用物理研究所提出了钍基熔盐堆核能系统(Thorium-based Molten Salt Reactor, TMSR)设计[6]。这些研究都是基于MSRE的研究成果提出的新概念设计。
由于熔盐堆的独特性,传统的固态燃料反应堆的物理模型已经无法适用,需要对熔盐堆建立新的物理模型。针对MSR的瞬态行为和燃料循环,许多研究机构已经做了相关研究。Lapenta等[7]使用点堆模型计算MSR中子物理参数;Kophazi等[8]使用蒙特卡罗核粒子输运程序MCNP4C计算由于熔盐的流动造成的DNP损失;Křepel等[9-10]在压水堆程序基础上发展了适用于MSR的中子动力学与热工水力学耦合程序DYN1D-MSR与DYN3D-MSR用于分析其安全特性;针对MOSART (Moderate Spectral Atmospheric Radiance and Transmittance)的特性,张大林等[11-12]发展使用了简化模型对其进行安全分析;针对ORNL的MSRE,庄坤等[13]开发了MOREL程序对其建模并进行动力学分析计算;胡天亮等[14]开发了稳态物理热工耦合程序计算其稳态工况下功率分布、流量分配等参数。
本文的主要工作是研究发展适用于熔盐堆的二维RZ圆柱几何时空中子动力学程序和与之耦合的热工水力学程序,并且以ORNL的MSRE为计算对象,建立物理模型,验证并计算熔盐堆的相关物理参数,讨论熔盐堆的物理特性并对熔盐堆进行安全特性分析。
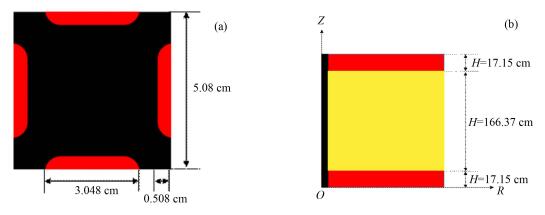
1 物理模型和计算方法 1.1 物理模型基于MSRE堆芯的结构特征[15],堆芯组件分布均匀,可以简化等效为轴对称模型。在本文的研究中,将MSRE堆芯在几何上简化为圆柱型结构,堆芯活性区半径为0.712 m,高度为2.007 m,堆芯高度为1.6637 m,其中填充熔盐石墨栅元;熔盐上下腔室高度都为0.1715 m,其中全部填充熔盐。堆芯示意图见图 1,图 1(a)为MSRE栅元格,图 1(b)为MSRE的RZ几何模型,堆芯中央为控制棒。MSRE实际堆芯中央有三个控制棒栅元,物理建模过程中按体积等效为一个控制棒栅元位于堆芯中央。控制棒的材料为Gd2O3-Al2O3,质量分数30%-70%[3]。
|
图 1 堆芯栅元(a)和RZ几何堆芯结构(b) Figure 1 Cell of MSRE (a) and schematic of core structure in RZ geometry (b). |
本文采用的MSRE熔盐相关参数及运行数据[15]如下所述,一回路熔盐燃料组分为LiF-BeF-ZrF4-UF4(摩尔分数比例65-29.2-5.0-0.8),其中铀富集度为235U 32%-238U 68%,密度为2263×(1-2.12×10-4×(T-650)) kg·m-3,比热容为1982.5 J·kg-1·℃-1,导热系数1.44 W·m-1·℃-1。堆芯石墨密度为1840.0 kg·m-3,比热容为1750.0J·kg-1·℃-1,导热系数30.0 W·m-1·℃-1。正常运行工况下,堆芯入口流速为0.0805 m3·s-1。
1.2 中子动力学模型 1.2.1 宏观群常数宏观群常数计算中将MSRE的熔盐通道组件等效为圆柱石墨通道,利用蒙特利尔大学开发的开源程序DRAGON4[16]对等效后石墨通道进行二维组件输运计算,得到相关材料栅元不同熔盐温度与石墨温度对应的群常数。对各个栅元组件输运计算得到快群和热群宏观群参数,提供给中子扩散方程进行扩散计算,温度反馈通过对不同温度点的宏观截面进行插值来实现。插值的具体方式如下:
| $ A=\frac{{{T}_{\text{salt}}}-{{T}_{\text{s1}}}}{{{T}_{\text{s2}}}-{{T}_{\text{s}}}_{\text{1}}} $ | (1) |
| $ B=\frac{{{T}_\text{gra}}-{{T}_{\text{g1}}}}{{{T}_{\text{g2}}}-{{T}_{\text{g}}}_{1}} $ | (2) |
| $ \begin{align} &\sum{({{T}_\text{salt}},{{T}_\text{gra}})}=AB\sum{({{T}_{\text{s2}}},{{T}_{\text{g2}}})}+ \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ A(1-B)\sum{({{T}_{\text{s}2}},{{T}_{\text{g1}}})}+ \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1-A)B\sum{({{T}_{\text{s1}}},{{T}_{\text{g2}}})}+ \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1-A)(1-B)\sum{({{T}_{\text{s1}}},{{T}_{\text{g1}}})} \\ \end{align} $ | (3) |
式中:∑(Tsalt, Tgra)为所需温度点的截面;T2、T1为使用DRAGON4计算的温度点。在计算过程中使用式(3) 对宏观截面进行插值计算得到所需温度的截面。
1.2.2 中子动力学计算方法中子动力学部分通过求解二维两群中子时空动力学方程,计算中子通量在堆芯RZ几何分布,式(4) 和(5) 分别是快群和热群通量对应的方程。由于管道内燃料流动会把缓发中子先驱核带出堆芯,在求解缓发中子先驱核浓度时考虑了DNP随熔盐沿轴向的流动迁移项,即式(6) 右边的
两群中子时空扩散方程及6组缓发中子先驱核方程:
| $ \begin{align} &\frac{1}{{{\upsilon }_{1}}}\frac{\partial {{\phi }_{1}}}{\partial t}=\nabla {{D}_{1}}\nabla {{\phi }_{1}}-{{\sum }_{1}}{{\phi }_{1}}+ \\ &\ \ \ \ \ \ \ \ \ \ (1-\beta )\left( {{v}_{1}}{{\sum }_{\text{f}1}}{{\phi }_{1}}+{{v}_{2}}{{\sum }_{\text{f2}}}{{\phi }_{2}} \right)+\sum\limits_{i=1}^{6}{{{\lambda }_{i}}{{C}_{i}}} \\ \end{align} $ | (4) |
| $ \frac{1}{{{\upsilon }_{2}}}\frac{\partial {{\phi }_{2}}}{\partial t}=\nabla {{D}_{2}}\nabla {{\phi }_{2}}-{{\sum }_{2}}{{\phi }_{2}}+{{\sum }_{1\to 2}}{{\phi }_{1}} $ | (5) |
| $ \begin{align} &\frac{\partial {{C}_{i}}}{\partial t}={{\beta }_{i}}\left( {{v}_{1}}{{\sum }_{\text{f1}}}{{\phi }_{1}}+{{v}_{2}}{{\sum }_{\text{f2}}}{{\phi }_{2}} \right)- \\ &\ \ \ \ \ \ \ \ {{\lambda }_{i}}{{C}_{i}}-\frac{\partial (V{{C}_{i}})}{\partial z},\ _{{}}^{_{{}}^{{}}}i=1,2,...,6 \\ \end{align} $ | (6) |
式中:φ1与φ2对应快群与慢群中子通量;υ1和υ2为快群和热群中子速度;∑f1和∑f2为快群和热群裂变截面;∑1和∑2为快群和热群吸收截面;D1和D2为快群和热群扩散系数;∑1→2为快群到热群的转移截面;Ci和λi为第i组缓发中子先驱核浓度和对应衰变常量;β为总的缓发中子份额;ν1和ν2为快群和热群裂变反应产生的中子;V为燃料盐的流速;
| $ \nabla D\nabla \phi =\frac{1}{r}\frac{\partial }{\partial r}(rD\frac{\partial \phi }{\partial r})+\frac{\partial }{\partial z}(D\frac{\partial \phi }{\partial z}) $ | (7) |
计算瞬态扩散方程时使用指数变换法[17],这种方法能够有效降低误差并减少计算时间。计算过程中假设φg=Ψgexp(ωt),Ci=χgexp(ωt),其中
求解中子扩散方程时,采用的边界条件如式(8),γ、σ为可调节参数,通过调节这两个参数,可以模拟出边界不同的反射率,一般情况下取σ=0时,γ=0为全反射边界条件,γ无穷大时为真空边界条件。在实际计算过程中可以采取不同数值的模拟不同的边界条件。本文计算MSRE采用真空边界条件。
| $ \frac{\partial }{\partial n}\phi +\gamma \phi =\sigma $ | (8) |
求解DNP衰变方程时,由于DNP会在堆芯外衰变,再重新流入堆内,所以采取下面的边界条件:Ci|z=0= Ci|z=Hexp(-λiTout)。其中,Tout是熔盐在堆外的循环时间,由熔盐的流速决定堆外循环时间的长短。
1.3 热工水力学模型 1.3.1 并联多通道水力学模型本文计算熔盐在堆芯管道内的流量分布时采用并联多通道模型[18],通过求解质量守恒方程(9)、动量守恒方程(10) 得到堆芯内熔盐流量在相应位置管道中的分配。
| $ \frac{\partial W}{\partial t}=\sum\limits_{i=1}^{N}{\frac{\partial {{W}_{i}}}{\partial t}} $ | (9) |
| $ \begin{align} &\int_{0}^{H}{\frac{1}{{{A}_{i}}}\frac{\partial {{W}_{i}}}{\partial t}\text{d}z}={{P}_{\text{in}}}-{{P}_{\text{out}}}-\int_{0}^{H}{\Delta {{P}_{a,i}}\text{d}z}-\int_{0}^{H}{\Delta {{P}_{f,i}}\text{d}z}- \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \int_{0}^{H}{\Delta {{P}_{ec,i}}\text{d}z}-\int_{0}^{H}{\Delta {{P}_{c,i}}\text{d}z} \\ \end{align} $ | (10) |
| $ \Delta {{P}_{a, i}}=\frac{\partial }{\partial z}(\frac{W_{i}^{2}}{{{A}_{i}}\rho (z)}) $ | (11) |
| $ \Delta {{P}_{f, i}}=\frac{fW_{i}^{2}}{2\rho (z)A_{i}^{2}{{D}_{i}}} $ | (12) |
| $ \Delta {{P}_{ec, i}}=\rho (z)g $ | (13) |
| $ \Delta {{P}_{c, i}}=\xi (z)\frac{W_{i}^{2}}{2\rho (z)A_{i}^{2}} $ | (14) |
式中:ΔPa, i表示加速度压降;ΔPf, i表示摩擦压降;ΔPec, i表示提升压降;ΔPc, i表示形阻压降;Wi表示各通道质量流量;Pin表示通道入口压力;Pout表示出口压力;ρ(z)表示相应高度的熔盐密度;Di表示通道的等效直径;Ai表示通道的横截面积;ξ(z)表示相应高度的形阻系数。由于堆芯内各通道在上下腔室都是连通的,所以各通道Pin与Pout都相等,利用等压降边界条件求解式(9)、(10) 来计算各个通道的流量Wi分布,得到对应通道的速度分布,利用得到的速度分布,计算堆芯DNP分布与熔盐温度分布。
1.3.2 传热模型在计算单根熔盐石墨管道内传热时,将MSRE的熔盐通道等效近似为圆柱石墨管道。式(15) 计算石墨管道中熔盐温度,假设石墨管道中熔盐温度只沿轴向分布,熔盐裂变反应释放的热功率由熔盐的轴向强迫对流换热导出。式(17) 与(18) 计算管道石墨温度,只计算石墨管道的径向热扩散,忽略轴向的热扩散,式(19) 表示管道边界为绝热边界条件。熔盐与石墨之间的热量交换由式(16) 计算。
| $ \begin{align} &\frac{\partial {{T}_{\operatorname{salt}}}(z,t)}{\partial t}=\frac{{{P}_{\operatorname{salt}}}(z,t)}{\text{ }\pi \text{ }{{R}^{2}}{{\rho }_\text{salt}}{{c}_\text{salt}}}-V(z,t)\frac{\partial {{T}_{\operatorname{salt}}}(z,t)}{\partial z}- \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{2h}{R{{\rho }_{\operatorname{salt}}}{{c}_{\operatorname{salt}}}}\left( {{T}_\text{salt}}(z,t)-{{T}_\text{gra}}(R,z,t) \right) \\ \end{align} $ | (15) |
| $ {{\varphi }_\text{cal}}(R, z, t)=h\left( {{T}_\text{salt}}(z, t)-{{T}_\text{gra}}(R, z, t) \right) $ | (16) |
| $ \begin{align} &{{\rho }_{\operatorname{gra}}}{{c}_\text{gra}}\frac{\partial {{T}_\text{gra}}(r,t)}{\partial t}=\frac{{{P}_\text{gra}}(z,t)}{\text{ }\pi \text{ }({{(R+e)}^{2}}-{{R}^{2}})}-\frac{1}{r}\frac{\partial (r{{\varphi }_\text{cal}})}{\partial r}(r,t) \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \forall z\in [0,H],\ r\in [R,R+e] \\ \end{align} $ | (17) |
| $ {{\varphi }_\text{cal}}(r, z, t)=-{{\lambda }_\text{gra}}\frac{\partial {{T}_\text{gra}}}{\partial t}\quad \forall z\in [0, H], \ r\in (R, R+e) $ | (18) |
| $ {{\varphi }_\text{cal}}(R+e, z, t)=0 $ | (19) |
式中:Tsalt和Tgra分别为熔盐和石墨温度;ρsalt和ρgra分别为熔盐和石墨密度;csalt和cgra分别为熔盐和石墨的比热容;φcal(R, z, t)和φcal(r, z, t)分别为熔盐到石墨的热流和石墨内部的热流;h为熔盐到石墨的对流换热系数;λgra为石墨的导热系数;R为熔盐管道半径;e为石墨管道径向厚度。
1.4 中子动力学与热工水力学耦合流程本文主要的计算思路是:将堆芯简化等效为RZ圆柱几何后划分网格,利用DRAGON4加工出每个网格的宏观截面并制表;求解RZ几何二维中子动力学方程,计算得到中子通量分布与堆芯能量分布;热工水力学计算时首先采用并联多通道模型,求解质量守恒方程和动量守恒方程,得到堆芯相应通道流量分布;再求解单通道传热模型计算熔盐与石墨温度。通过对宏观截面库插值实现耦合计算:将堆芯中子动力学与热工水力学耦合在一起。通过上述计算流程可以得到稳态下堆芯的通量、温度、流量分布,及各种瞬态工况下相关参数。
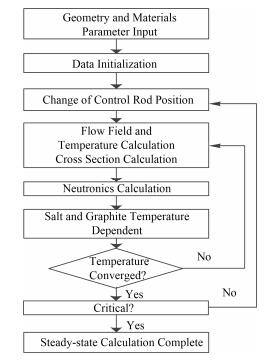
1.4.1 稳态计算图 2是稳态计算的耦合方法与计算流程。具体方法是:首先在计算开始时读入堆芯相关数据,进行参数初始化,计算稳态扩散方程的相关系数。使用并联多通道模型计算堆芯相应通道流量分布,并计算得到速度分布。使用有限差分法计算稳态扩散方程及DNP衰变方程,进行迭代计算相应的φ(r, z)、C(r, z)与keff。利用通量分布计算得到对应几何网格内能量分布,求解传热方程得到相应的熔盐温度与石墨温度分布,并对熔盐温度进行收敛迭代计算。通过调整控制棒的位置,使keff收敛至1.0,计算出临界堆芯通量分布与温度分布作为瞬态工况的初始值。
|
图 2 稳态计算流程 Figure 2 Flow diagram of static coupling schemes. |
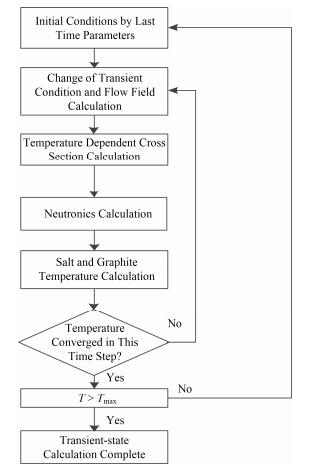
图 3为瞬态计算的耦合方法与计算流程。具体方法是:将堆芯临界稳态参数作为瞬态工况开始时的参数,瞬态开始后,堆芯状态发生变化,首先计算堆芯入口总流量改变时堆芯相应通道熔盐流量分布及对应的熔盐速度分布,利用得到的熔盐速度分布求解堆芯瞬态扩散方程及DNP衰变方程,计算得到通量分布与DNP分布,再求解堆芯传热方程,计算得到熔盐温度与石墨温度分布,对相关参数进行收敛迭代使其在一个时间步内都收敛。通过进行瞬态工况计算,可以得到堆芯状态发生变化后的堆芯中子通量、DNP及温度等相关参数的变化情况,以此对熔盐堆进行安全特性分析。
|
图 3 瞬态计算流程 Figure 3 Flow diagram of time-dependent coupling schemes. |
本文利用MSRE的相关实验数据,对程序进行验证计算:MSRE在稳态运行时,由于熔盐流动,堆芯部分DNP流出堆芯在堆外衰变,造成堆芯有效DNP份额下降,通过计算堆芯内有效DNP份额可以得出MSRE在运行过程中由于熔盐的流动造成的DNP的损失份额;计算零功率临界情况下恒功率启泵与停泵瞬态,通过调节控制棒使堆芯保持临界,通过控制棒的位置变化可得出堆芯反应性的变化情况;验证计算了MSRE自然循环过程中的功率与出口温度等参数。最后计算分析了熔盐进入堆芯时过冷却和过加热两种情况下堆芯功率及出口温度变化,以及在无保护情况下停泵时堆芯功率的变化。
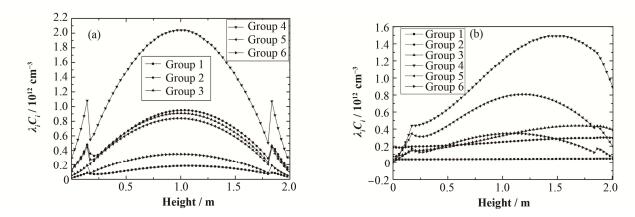
2.1 熔盐流动与不流动情况下堆芯DNP分布图 4(a)、(b)分别是熔盐不流动与流动情况下6组缓发中子源强λiCi沿轴向的分布。熔盐流动时堆芯入口流量为0.0805 m3·s-1,可以清楚地观察到由于熔盐的流动造成λiCi分布与不流动情况下差别很大。由于堆芯石墨区和上下腔室燃料装载不同,缓发中子源强的分布在两者交界面处存在阶跃现象。计算稳态λiCi分布时,堆芯入口的熔盐流量为0.00039 m3·s-1,从图 4(a)可以看到,λiCi呈现对称分布,与传统固态反应堆一致。图 4(b)为熔盐流动时λiCi分布,由于各组DNP的衰变常数不同,在相同的堆外循环时间内,各组DNP衰变的比例也不同。使用前文所说的DNP边界条件计算,可以得到在堆外循环过程完重新进入堆芯后的各组DNP浓度,从而得到入口处即堆芯底部各组λiCi。
|
图 4 MSRE中DNP沿轴向分布(a)熔盐不流动,(b)正常流动 Figure 4 DNP axial distribution in MSRE. (a) No-flow, (b) Normal flow |
正是由于熔盐流动引起各组λiCi在堆芯分布的变化造成MSR的物理参数与固体燃料反应堆有较大差别,需要专门研究能够准确模拟MSR物理参数的计算程序。
2.2 在熔盐流动下堆芯DNP流失份额由于堆芯熔盐的流动,堆芯内部分DNP会流出堆芯在堆外衰变造成堆芯内反应性损失。表 1为计算的堆芯有效DNP份额,及堆芯入口熔盐流量0.0805 m3·s-1时,6组DNP流出堆芯的损失份额与参考值的比较。堆芯有效DNP份额是通过求解中子扩散方程与DNP衰变方程得到堆芯DNP分布,再利用中子价值对DNP做权重计算得到,以此为基础可以得到堆芯在各种工况下的反应性损失。从表 1中可以看出,本文计算结果与参考值及其他单位的计算结果都较为吻合,有偏差的原因应该是MSRE物理建模过程中所采用的简化模型不同。表 1中βeff static是熔盐不流动情况计算的β static的值,βloss是熔盐流动所造成的反应性损失。
| 表 1 MSRE中DNP份额的损失 Table 1 DNP loss in MSRE. |
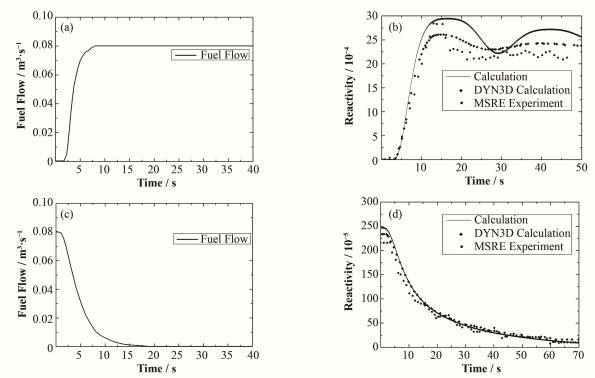
本文模拟计算MSRE在零功率时启泵与停泵瞬态,图 5(a)为启泵时堆芯入口体积流速[15],图 5(b)为启泵时反应性的变化。由于在启泵后,堆芯入口熔盐流量增加,堆芯部分DNP被带出堆芯而在堆外衰变,堆芯反应性下降,需要提升控制棒维持堆芯临界。部分DNP随着熔盐流出堆芯后在堆外循环过程中衰变,但随着熔盐完成堆外循环流回堆芯后,未衰变的DNP再次返回堆芯,使得堆芯反应性增加,控制棒需要作相应的回落。从图 5(b)可见,约13 s时,反应性发生波动,是由于堆外未衰变的DNP重新进入堆芯。本文在计算结果处理时,将控制棒的位移通过控制棒的积分价值转换为反应性的变化,可以发现模拟计算的结果基本同MSRE实验数据相吻合,存在的误差可能是本文计算过程中熔盐在堆外循环时间与实际运行工况有差别所导致。
|
图 5 零功率启泵与停泵时MSRE堆芯反应性变化 Figure 5 Reactivity compensation in the case of fuel pump start and coast-down transients at zero-power. |
图 5(c)为停泵时堆芯入口体积流速变化[15],图 5(d)为停泵时反应性的变化。停泵后堆芯熔盐流速迅速下降,堆芯内DNP的份额增加,使得堆芯反应性增加,需要将控制棒插入使得堆芯功率恒定。通过控制棒的移动,使得堆芯功率守恒,可以发现由于停泵,堆芯DNP增加使得堆芯反应性增加了2.3685×10-3。
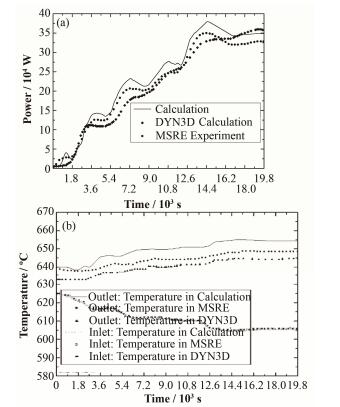
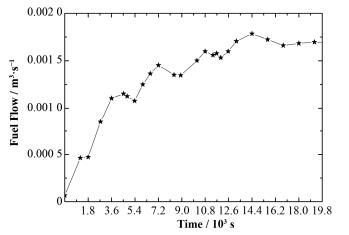
2.4 自然循环计算由于本文中无法计算自然循环时交换器中的换热情况,因此无法计算自然循环过程中堆芯入口流量与堆芯入口温度的变化情况,所以采用将堆芯入口流量与堆芯入口温度作为输入参数,计算自然循环过程中堆芯功率与出口温度变化情况。图 6(a)为功率变化情况,图 6(b)为有堆芯入口温度与堆芯出口温度变化情况。在给定堆芯入口流量与入口温度[15]时,堆芯功率与堆芯出口温度基本能同MSRE实验结果与其他计算结果相吻合。图 6(b)中计算得到的出口温度与实验数据相比偏高,是由于计算的功率也偏高造成的,这个误差应该是由于本文在计算过程中建立模型与实际模型有差别导致的。图 7是自然循环过程中堆芯熔盐流速变化[15]。
|
图 6 自然循环期间反应堆功率(a)与堆芯出口温度(b)变化 Figure 6 The change of power (a) and outlet temperature (b) in the natural circulation experiment. |
|
图 7 自然循环过程中堆芯熔盐流速变化 Figure 7 The change of flow in the natural circulation experiment. |
MSRE具有负温度反应性系数,堆芯熔盐温度升高会引入负反应性,温度降低会引入正反应性。为了观察熔盐入口温度变化对堆芯功率及出口温度的影响,本文计算了堆芯零功率运行时,熔盐在进入堆芯时发生过加热和过冷却两种情况。
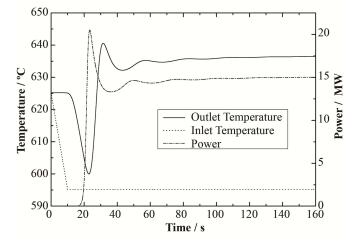
在熔盐进入堆芯时过冷却的情况下,堆芯入口温度在10 s之内下降30 ℃,由于熔盐的负温度反应性系数,堆芯温度下降将引入大量反应性,造成堆芯功率从零功率情况下增大到兆瓦级别。堆芯功率增大后,堆芯熔盐温度上升,造成出口温度在一开始受到入口温度的影响下降后迅速增加,而堆芯温度增加后重新引入负反应性,造成功率震荡逐渐平衡,使得堆芯重新稳定下来,具体结果见图 8。
|
图 8 堆芯入口温度10 s内下降30 ℃后的堆芯功率及出口温度变化 Figure 8 The change of power and outlet temperature in the case of inlet temperature decrease in 10 s. |
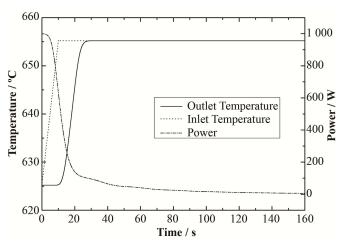
在熔盐进入堆芯过加热的情况下,堆芯入口温度在10 s内上升30 ℃。由于熔盐的负温度反应性系数,堆芯内的熔盐温度上升会引入大量负反应性,造成堆芯功率急剧下降到接近0值。堆芯出口温度主要受入口温度影响,具体结果见图 9。
|
图 9 堆芯入口温度10 s内上升30 ℃后的堆芯功率及出口温度变化 Figure 9 The change of power and outlet temperature in the case of inlet temperature crease in 10 s. |
从上述两个结果中可以发现,在零功率情况下,熔盐堆的堆芯入口熔盐过冷与过热情况,由于温度的负反馈效应,最终都能使堆芯功率与出口温度重新达到一个新的平衡态,不会造成堆芯功率持续升高发生堆芯熔毁事故而使堆芯处于安全状态。
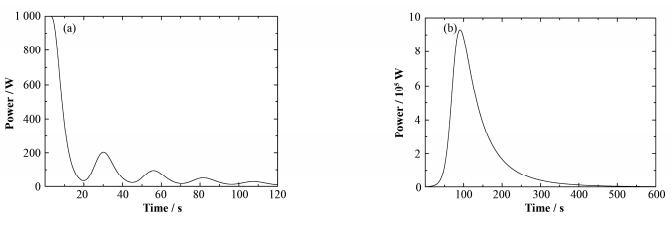
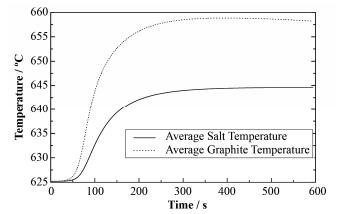
2.6 零功率情况下无保护启泵与停泵时功率变化零功率无保护启泵时,由于堆芯DNP随熔盐流出堆芯,此时控制棒位置不变,则堆芯反应性损失而不能临界,堆芯功率迅速下降。随着熔盐的流动,流出堆芯的DNP重新流回堆芯后,会使得堆芯功率有上下浮动,最终功率水平接近于0而停堆。而停泵情况下,熔盐流量的降低导致流出堆芯的DNP减少,引起堆芯反应性上升,功率在最初2 min内急剧上升,后来由于堆芯温度上升。两种工况下的堆芯功率变化见图 10,停泵时堆芯温度变化见图 11。由图 11可以发现,堆芯熔盐平均温度与石墨平均温度迅速升高,引入负反应性,并且负反应性大于未在堆芯外衰变的DNP所引入的正反应性后,堆芯功率下降,并且由于堆芯温度上升持续引入的负反应性使得堆芯功率一直下降,最终熔盐堆处于功率非常低的状态。
|
图 10 零功率情况下无保护启泵(a)与停泵(b)时功率变化 Figure 10 The change of power in the case of unprotected fuel pump start (a) and coast-down transients (b) at zero-power. |
|
图 11 零功率情况下无保护停泵时堆芯温度变化 Figure 11 The change of salt and graphite temperature in the case of unprotected fuel pump coast-down transients at zero-power. |
由于熔盐堆中熔盐流动的独有特性,使得熔盐堆与传统固态反应堆存在很多不同之处,本文主要是在考虑熔盐流动性的基础上,建立了适用于熔盐堆的中子动力学与热工水力学相耦合的模型,并利用MSRE实验数据对耦合模型进行了验证,计算了MSRE正常工况下堆芯有效DNP份额,恒功率启停泵时堆芯内反应性的变化及自然循环时堆芯功率及出口温度的变化,计算结果与实验值吻合较好,表明本文建立的模型基本能用于MSRE的模拟计算。并且利用建立的模型对MSRE进行了安全分析,计算了熔盐堆入口温度过冷和过热情况下堆芯功率及出口温度变化,发现堆芯入口温度在过冷和过热两种情况下都不会造成堆芯功率持续升高引起堆芯熔毁;最后计算了无保护启泵与停泵时,堆芯功率随时间的变化情况,及停泵时堆芯熔盐平均温度与石墨平均温度随时间的变化情况,结果表明零功率启停泵时,控制棒位置不发生变化,堆芯最终也都处于安全状态。从本文的计算结果可以分析得出熔盐堆具有固有安全性。
| [1] |
Doe U. A technology roadmap for generation IV nuclear energy systems[C]. Proceedings of the Nuclear Energy Research Advisory Committee and the Generation IV International Forum, 2002:239-241.
|
| [2] |
Macpherson H. The molten salt reactor adventure[J]. Nuclear Science and Engineering, 1985, 90(4): 374-380. DOI:10.13182/nse90-374 |
| [3] |
Haubenreich P. Molten-salt reactor experiments[R]. Oak Ridge National Laboratory, 1970:4396.
|
| [4] |
Vergnes J, Lecarpentier D, Garzenne C, et al. The AMSTER concept[C]. Proceedings of the proceedings of the 6th OECD/NEA Information Exchange Meeting on Actinide and Fission Product Partitioning and Transmutation, Madrid, Spain, 2000.
|
| [5] |
Sekimoto H. Innovative nuclear reactor development for future[R]. Inter-COE, 2006:1.
|
| [6] |
江绵恒, 徐洪杰, 戴志敏. 未来先进核裂变能——TMSR核能系统[J]. 中国科学院院刊, 2012(3): 366-374. JIANG Mianheng, XU Hongjie, DAI Zhimin. Advanced fission energy program-TMSR nuclear energy system[J]. Bulletin of Chinese Academy of Sciences, 2012(3): 366-374. DOI:10.3969/j.issn.1000-3045.2012.03.016 |
| [7] |
Lapenta G, Mattioda F, Ravetto P. Point kinetic model for fluid fuel systems[J]. Annals of Nuclear Energy, 2001, 28(17): 1759-1772. DOI:10.1016/s0306-4549(01)00012-3 |
| [8] |
Kophazi J, Szieberth M, Feher S, et al. MCNP based calculation of reactivity loss in circulating fuel reactors[J]. Nuclear Mathematical and Computational Sciences, 2003. |
| [9] |
Křepel J, Grundmann U, Rohde U, et al. DYN1D-MSR dynamics code for molten salt reactors[J]. Annals of Nuclear Energy, 2005, 32(17): 1799-1824. DOI:10.1016/j.anucene.2005.07.007 |
| [10] |
Křepel J, Rohde U, Grundmann U, et al. DYN3D-MSR spatial dynamics code for molten salt reactors[J]. Annals of Nuclear Energy, 2007, 34(6): 449-462. DOI:10.1016/j.anucene.2006.12.011 |
| [11] |
Zhang D L, Qiu S Z, Su G H. Development of a safety analysis code for molten salt reactors[J]. Nuclear Engineering and Design, 2009, 239(12): 2778-2785. DOI:10.1016/j.nucengdes.2009.08.020 |
| [12] |
Zhang D L, Qiu S Z, Su G H, et al. Analysis on the neutron kinetics for a molten salt reactor[J]. Progress in Nuclear Energy, 2009, 51(4): 624-636. DOI:10.1016/j.pnucene.2008.11.008 |
| [13] |
庄坤, 曹良志, 郑友琦, 等. 熔盐堆动力学软件开发[J]. 核动力工程, 2014, S2: 183-185. ZHUANG Kun, CAO Liangzhi, ZHENG Youqi, et al. Development of neutron kinetic code for molten salt reactors[J]. Nuclear Power Engineering, 2014, S2: 183-185. |
| [14] |
胡田亮, 吴宏春, 曹良志, 等. 熔盐堆稳态物理-热工耦合计算研究[J]. 原子能科学技术, 2016, 50(10): 1823-1827. HU Tianliang, WU Hongchun, CAO Liangzhi, et al. Neutronics and thermal-hydraulics coupling analysis of molten salt reactor at steady state[J]. Atomic Energy Science and Technology, 2016, 50(10): 1823-1827. DOI:10.7538/yzk.2016.50.10.1823 |
| [15] |
Křepel J. Dynamics of molten salt reactor[D]. Prague:Czech Technical University, 2006.
|
| [16] |
Marleau G, Ebert A, Roy R. A user guide for DRAGON[R]. Version 4. Institut de génie nucléaire, Département de génie mécanique, École Polytechnique de Montréal, 2011.
|
| [17] |
Cho N Z. Fundamentals and recent developments of reactor physics methods[J]. Nuclear Engineering and Technology, 2005, 37(1): 25-78. |
| [18] |
李磊, 张志俭. 并联通道瞬态流量分配方法研究[J]. 核动力工程, 2010, 31(5): 97-101. LI Lei, ZHANG Zhijian. Research on transient flux distribution in parallel channels[J]. Nuclear Power Engineering, 2010, 31(5): 97-101. |


